18.1.1平行四边形的性质 课件
图片预览






文档简介
课件30张PPT。《数学》( 北师大.七年级 下册 )18.1.1平行四边形的性质(一) 学校准备美化校园,想要给学校花园设计一个造型,花园里目前已经栽了三棵(如图)树,现在学校又购买了一颗,希望这四棵树能组成一个平行四边形,第四棵树应该栽在哪里呢?18.1 平行四边形的性质(第一课时)2、掌握平行四边形的性质,并能够利用性质进行简单的推理计算。1、掌握平行四边形有关概念.学习目标预习检测活 动 一例题赏析达标测试拓展测试谈谈收获活 动 二 研读课本41页第1、2自然段,看图回答下列问题:只有充分预习,才会有丰富多彩的课堂展示。预习检测学习目标活 动 一例题赏析达标测试拓展测试谈谈收获活 动 二1、定义:2、记作:4、几何语言: ∴四边形ABCD是平行四边形在四边形ABCD中,
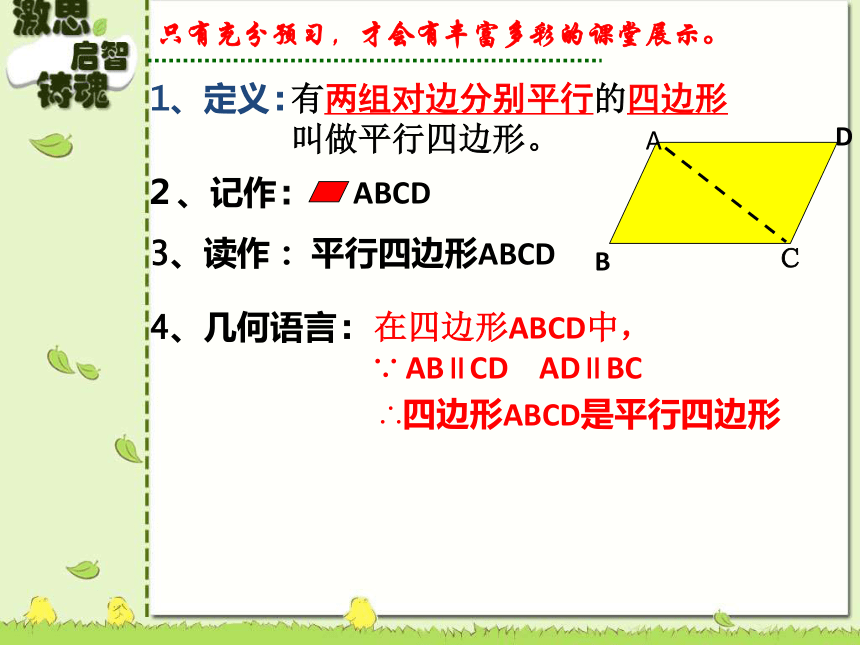
∵ AB∥CD AD∥BC3、读作:有两组对边分别平行的四边形
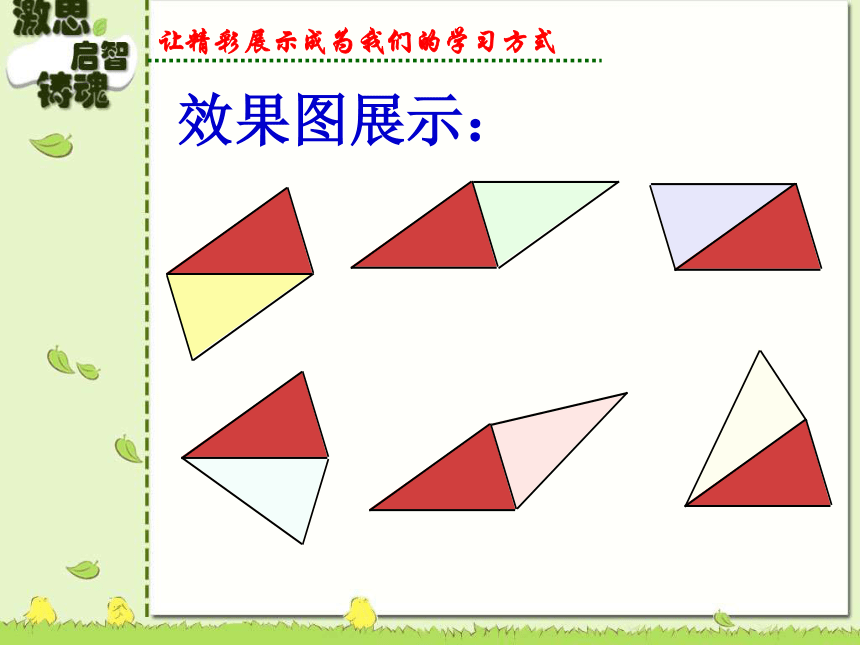
叫做平行四边形。平行四边形ABCD只有充分预习,才会有丰富多彩的课堂展示。 拿出你准备好的两个全等的三角形纸片,并将它们相等的一组边重合,可以得到四边形吗?你有几种方案?在你拼出的四边形中有平行四边形吗?你能结合平行四边形的定义给出合理的解释吗?拼一拼团结合作、深入探究、激情澎湃活 动 一学习目标预习检测例题赏析达标测试拓展测试谈谈收获活 动 二效果图展示:让精彩展示成为我们的学习方式 如图,EF∥ AD ,GH∥ CD,
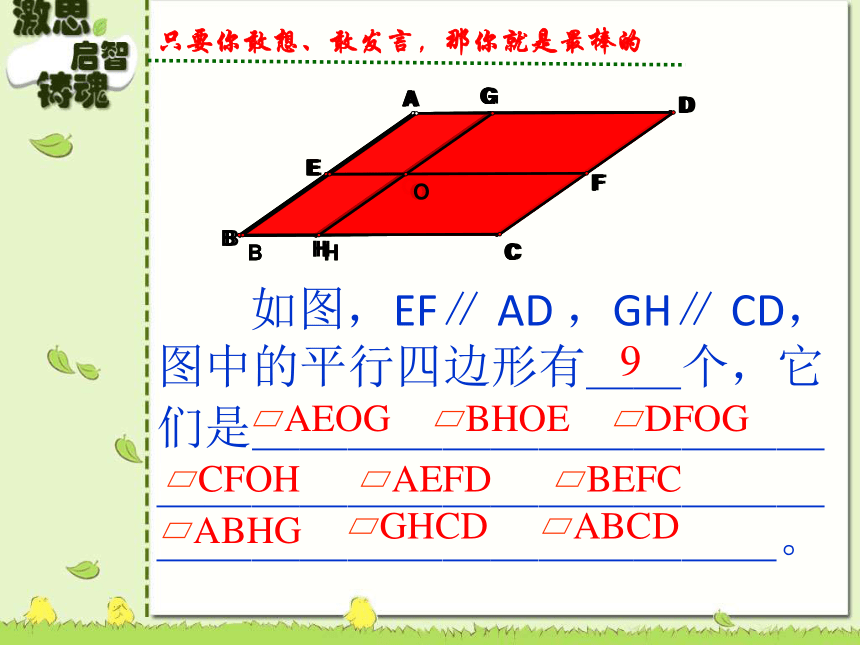
图中的平行四边形有__个,它
们是_______________________________________。9AEOGDFOGBHOEAEFDCFOHBEFCABCDGHCDABHG只要你敢想、敢发言,那你就是最棒的 根据定义画一个平行四边形,观察这个四边形,除了 “两组对边分别平行”以外,它的边、角之间有什么关系吗?度量一下,是不是和你的猜想一致?还有别的方法吗?心动不如行动,跃跃欲试不如亲自尝试活 动 二学习目标预习检测例题赏析达标测试拓展测试谈谈收获活 动 一猜想:
平行四边形的对边相等
平行四边形的对角相等插上好奇的翅膀,探索数学的奥秘观察并作出猜想方法1:度量法猜想:
平行四边形的对边相等
平行四边形的对角相等你能验证你的猜想吗?插上好奇的翅膀,探索数学的奥秘方法2:推理证明DCBA推理证明已知:如图, □ ABCD求证:AB=CD,BC=AD, ∠B= ∠D,
∠A= ∠C4123DCBA即∠ADC=∠ABC证明:连结BD∵AB∥CD,AD∥BC
(平行四边形的对边平行)∴∠1=∠2,∠3=∠4∠1=∠2,BD=DB,∠3=∠4∴AB=CD,BC=DA,∠A=∠C又∵∠1=∠2,∠3=∠4∴∠1+∠4=∠2+∠3在 ABD 和 CDB中平行四边形的性质平行四边形
的平行四边形
的平行四边形
的∵四边形ABCD是平行四边形
∴ ∥ ∥∵四边形ABCD是平行四边形
∴ = =∵四边形ABCD是平行四边形
∴ = =对边平行ABCDADBCABCDADBC∠A∠B ∠D∠C 对边相等对角相等56°124°56°124°56o124o124o∠B =____,∴ ∠BAD+ ∠B = 180° ∵ AD∥BC ∠D=____.结论:平行四边形的邻角 .互补2、□ ABCD中, AB=3cm, BC=5cm, 则AD= ,CD= .3、在□ABCD中,∠A+∠C=120°,
∠B= ;∠D= ;50°130°130°3cm5cm120°120° 小明用一根36m
长的绳子围成了一个平行四边形场地,其
中一条边AB长为8m,其他三条边各长多少?解:∵四边形ABCD是平行四边形
∴AB = CD,AD=BC
∵AB=8,
∴CD=8(m)
又AB+BC+CD+AD=36.
∴AD=BC=10(m)
例题赏析学习目标预习检测活 动 二达标测试拓展测试谈谈收获活 动 一达标测试达标测试学习目标预习检测活 动 二例题赏析拓展测试谈谈收获活 动 一132°48°3 cm1、平行四边形ABCD中,BC=3cm,
∠A= 48°则: ∠B=_____, ∠C=_____ , AD=_______.变题1、 的周长是20,已知AB=6,则
BC=__,CD=__.46510拓展测试拓展测试学习目标预习检测活 动 二例题赏析达标测试谈谈收获活 动 一1 .如果□ABCD的周长为40cm,△ABC的周长为25cm,则对角
线AC的长是( ) cm
A. 5 B. 15 C. 6 D. 16A2.在□ABCD中,AE⊥BD,CF⊥BD垂足为E、F,那么BE与DF相等吗?说说你的理由. 本节课我们对平行四边
形的概念及性质进行讨论与
学习,你有何新的收获?七嘴八舌说一说谈谈收获学习目标预习检测活 动 二例题赏析达标测试拓展测试活 动 一小结:
一、知识点:
1.平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质:
对边平行且相等,对角相等.
二、学习方法:
转化思想:解决平行四边形的有关问题经常
连结对角线转化为三角形。 学校准备美化校园,想要给学校花园设计一个造型,花园里目前已经栽了三棵(如图)树,现在学校又购买了一颗,希望这四棵树能组成一个平行四边形,第四棵树应该栽在哪里呢? 选做题:
如图,在平行四边形ABCD中,
以一组对边AD、BC向外作等边 ADE和 BCF,连接BE、DF,探索BE、DF的大小关系。
谢谢!再见!
∵ AB∥CD AD∥BC3、读作:有两组对边分别平行的四边形
叫做平行四边形。平行四边形ABCD只有充分预习,才会有丰富多彩的课堂展示。 拿出你准备好的两个全等的三角形纸片,并将它们相等的一组边重合,可以得到四边形吗?你有几种方案?在你拼出的四边形中有平行四边形吗?你能结合平行四边形的定义给出合理的解释吗?拼一拼团结合作、深入探究、激情澎湃活 动 一学习目标预习检测例题赏析达标测试拓展测试谈谈收获活 动 二效果图展示:让精彩展示成为我们的学习方式 如图,EF∥ AD ,GH∥ CD,
图中的平行四边形有__个,它
们是_______________________________________。9AEOGDFOGBHOEAEFDCFOHBEFCABCDGHCDABHG只要你敢想、敢发言,那你就是最棒的 根据定义画一个平行四边形,观察这个四边形,除了 “两组对边分别平行”以外,它的边、角之间有什么关系吗?度量一下,是不是和你的猜想一致?还有别的方法吗?心动不如行动,跃跃欲试不如亲自尝试活 动 二学习目标预习检测例题赏析达标测试拓展测试谈谈收获活 动 一猜想:
平行四边形的对边相等
平行四边形的对角相等插上好奇的翅膀,探索数学的奥秘观察并作出猜想方法1:度量法猜想:
平行四边形的对边相等
平行四边形的对角相等你能验证你的猜想吗?插上好奇的翅膀,探索数学的奥秘方法2:推理证明DCBA推理证明已知:如图, □ ABCD求证:AB=CD,BC=AD, ∠B= ∠D,
∠A= ∠C4123DCBA即∠ADC=∠ABC证明:连结BD∵AB∥CD,AD∥BC
(平行四边形的对边平行)∴∠1=∠2,∠3=∠4∠1=∠2,BD=DB,∠3=∠4∴AB=CD,BC=DA,∠A=∠C又∵∠1=∠2,∠3=∠4∴∠1+∠4=∠2+∠3在 ABD 和 CDB中平行四边形的性质平行四边形
的平行四边形
的平行四边形
的∵四边形ABCD是平行四边形
∴ ∥ ∥∵四边形ABCD是平行四边形
∴ = =∵四边形ABCD是平行四边形
∴ = =对边平行ABCDADBCABCDADBC∠A∠B ∠D∠C 对边相等对角相等56°124°56°124°56o124o124o∠B =____,∴ ∠BAD+ ∠B = 180° ∵ AD∥BC ∠D=____.结论:平行四边形的邻角 .互补2、□ ABCD中, AB=3cm, BC=5cm, 则AD= ,CD= .3、在□ABCD中,∠A+∠C=120°,
∠B= ;∠D= ;50°130°130°3cm5cm120°120° 小明用一根36m
长的绳子围成了一个平行四边形场地,其
中一条边AB长为8m,其他三条边各长多少?解:∵四边形ABCD是平行四边形
∴AB = CD,AD=BC
∵AB=8,
∴CD=8(m)
又AB+BC+CD+AD=36.
∴AD=BC=10(m)
例题赏析学习目标预习检测活 动 二达标测试拓展测试谈谈收获活 动 一达标测试达标测试学习目标预习检测活 动 二例题赏析拓展测试谈谈收获活 动 一132°48°3 cm1、平行四边形ABCD中,BC=3cm,
∠A= 48°则: ∠B=_____, ∠C=_____ , AD=_______.变题1、 的周长是20,已知AB=6,则
BC=__,CD=__.46510拓展测试拓展测试学习目标预习检测活 动 二例题赏析达标测试谈谈收获活 动 一1 .如果□ABCD的周长为40cm,△ABC的周长为25cm,则对角
线AC的长是( ) cm
A. 5 B. 15 C. 6 D. 16A2.在□ABCD中,AE⊥BD,CF⊥BD垂足为E、F,那么BE与DF相等吗?说说你的理由. 本节课我们对平行四边
形的概念及性质进行讨论与
学习,你有何新的收获?七嘴八舌说一说谈谈收获学习目标预习检测活 动 二例题赏析达标测试拓展测试活 动 一小结:
一、知识点:
1.平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质:
对边平行且相等,对角相等.
二、学习方法:
转化思想:解决平行四边形的有关问题经常
连结对角线转化为三角形。 学校准备美化校园,想要给学校花园设计一个造型,花园里目前已经栽了三棵(如图)树,现在学校又购买了一颗,希望这四棵树能组成一个平行四边形,第四棵树应该栽在哪里呢? 选做题:
如图,在平行四边形ABCD中,
以一组对边AD、BC向外作等边 ADE和 BCF,连接BE、DF,探索BE、DF的大小关系。
谢谢!再见!
