8.1 认识不等式同步练习
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
8.1 认识不等式同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.用不等号“<”或“>”表示不等关系的式子,叫做不等式.
2.不等式的解:能使不等式成立的未知数的值 叫做不等式的解.
3.列不等式:应注意“不大于”、“不小于”、“非负数”、“非正数”等关键词,并能准确地用不等号表示.21·cn·jy·com
基础知识和能力拓展精练
一、选择题
1.下列式子:①<y+5;②1>-2;③3m-1≤4;④a+2≠a-2中,不等式有( )
A. 2个 B. 3个 C. 4个 D. 1个
2.x与3的和的一半是负数,用不等式表示为( )
A. x+3>0 B. x+3<0 C. (x+3)<0 D. (x+3)>0
3.“a<b”的反面是( )
A. a≠b B. a>b C. a≥b D. a=b
4.据中央气象台报道,某日上海最高气温是22 ℃,最低气温是11 ℃,则当天上海气温t(℃)的变化范围是( )www.21-cn-jy.com
A. t>22 B. t≤22 C. 11<t<22 D. 11≤t≤22
5.当x=3时,下列不等式成立的是( )
A. x+3>5 B. x+3>6 C. x+3>7 D. x+3<5
6.高钙牛奶的包装盒上注明“每100克内含钙≥150毫克”,它的含义是指( )
A. 每100克内含钙150毫克 B. 每100克内含钙高于150毫克
C. 每100克内含钙不低于150毫克 D. 每100克内含钙不超过150毫克
7.6月8日我县最高气温是29℃,最低气 ( http: / / www.21cnjy.com )温是19℃,则当天我县气温t(℃)的变化范围是( )
A.19≤t≤29 B.t<19 C.t≤19 D.t≥29【来源:21cnj*y.co*m】
8.下列按条件列出的不等式中,正确的是( )
A. a不是负数,则a>0 B. a与3的差不等于1,则a-3<1
C. a是不小于0的数,则a>0 D. a与 b的和是非负数,则a+b≥0
9.5名学生身高两两不同,把他们按从高到低 ( http: / / www.21cnjy.com )排列,设前三名的平均身高为a米,后两名的平均身高为b米.又前两名的平均身高为c米,后三名的平均身高为d米,则( )
A. > B. > C. = D. 以上都不对
10. x=3是下列哪个不等式的解 ( )
A.x+2>4 B.x2-3>6 C.2x-1<3 D.3x+2<10
二、填空题
11.给出下列表达式:①a(b+c)=ab ( http: / / www.21cnjy.com )+ac;②﹣2<0;③x≠5;④2a>b+1;⑤x2﹣2xy+y2;⑥2x﹣3>6,其中不等式的个数是_______.
12.用不等式表示下列关系:x的3倍与8的和比y的2倍小:_______.
13.如图,身高为 ( http: / / www.21cnjy.com )xcm的1号同学与身高为ycm的2号同学站在一起时,如果用一个不等式来表示他们的身高关系,则这个式子可以表示成x_____y(用“>”或“<”填空).
( http: / / www.21cnjy.com )
1号 2号
14.有理数m,n在数轴上如图,用不等号填空.
(1)m+n______0;(2)m-n______0;(3)m n______0;(4)m2______n;(5)|m|______|n|.
15.k的值大于﹣1且不大于3,则用不等式表示 k的取值范围是_____.(使用形如a≤x≤b的类似式子填空.)【出处:21教育名师】
16.按商品质量规定:商店出售的标明5 ( http: / / www.21cnjy.com )00 g的袋装食盐,其实际克数与所标克数相差不能超过5 g.设实际克数为x(g),则x应满足的不等式是_____.21*cnjy*com
三、解答题
17.用适当的符号表示下列关系:
(1)一枚炮弹的杀伤半径不小于300米;
(2)三件上衣与四条长裤的总价钱不高于268元;
(3)明天下雨的可能性不小于70%;
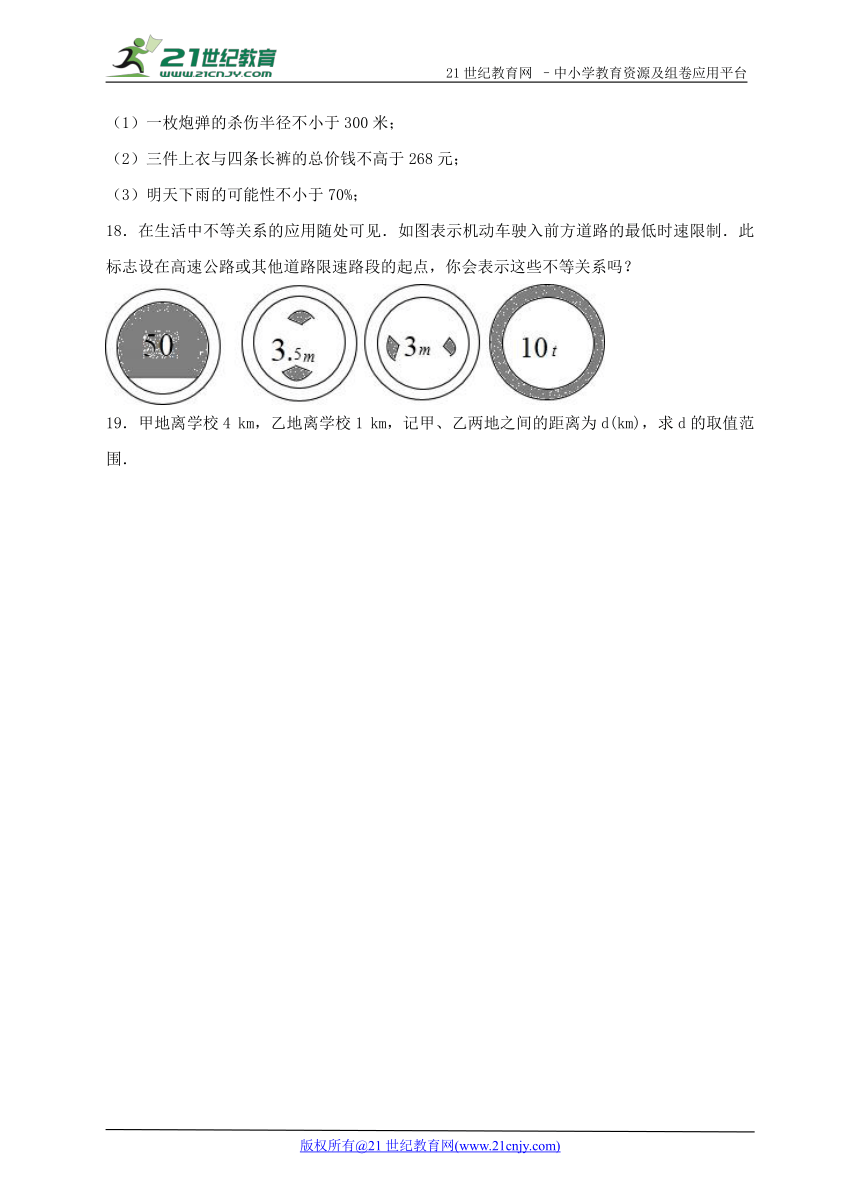
18.在生活中不等关系的应用随处可 ( http: / / www.21cnjy.com )见.如图表示机动车驶入前方道路的最低时速限制.此标志设在高速公路或其他道路限速路段的起点,你会表示这些不等关系吗?
( http: / / www.21cnjy.com )
19.甲地离学校4 km,乙地离学校1 km,记甲、乙两地之间的距离为d(km),求d的取值范围.
参考答案
1.C
【解析】根据不等式的定义:“用不等号表示两个量间的不等关系的式子叫做不等式”分析可知,上述四个式子都是不等式.21教育名师原创作品
故选C.
2.C
【解析】“与3的和的一半是负数”用不等式表示为:
.
故选C.
3.C
【解析】a<b的反面是a=b或a>b,即a≥b.
故选C.
4.D
【解析】气温最高是22℃,则t≤22;
气温最低是11℃,则t≥11.
故气温的变化范围11≤t≤22.
故选D.
5.A
【解析】A项,当x=3时,x+3= ( http: / / www.21cnjy.com )3+3=6>5,所以x+3>5成立;B项,当x=3时,x+3=3+3=6,所以x+3>6不成立;C项,当x=3时,x+3=3+3=6<7,所以;x+3>7不成立;D项,当x=3时,x+3=3+3=6>5,所以x+3<5不成立.21*cnjy*com
故选:A
6.C
【解析】根据≥的含义,“每100克内含钙≥150毫克”,就是“每100克内含钙不低于150毫克”,
故选:C.
7.A
【解析】读懂题意,找到最高气温和最低气温即可 ( http: / / www.21cnjy.com ).
解:因为最低气温是19℃,所以19≤t,最高气温是29℃,t≤29,
则今天气温t(℃)的范围是19≤t≤29.
故选A.
8.D
【解析】根据a不是负数,则a可能是正数和0,即a≥0,故不正确;
根据a与3的差不等于1,可知a-3≠1,故不正确;
根据a是不小于0的数,即可知a≥0,故不正确;
根据非负数的意义,可知a+b≥0,故正确.
故选:D
9.B
【解析】根据把他们按从高到低排列,设前三名的平均身高为a米,后两名的平均身高为b米.又前两名的平均身高为c米,后三名的平均身高为d米,则c>a>d>b,则c-a>0>b-d,得c+d>a+b,得: >.21世纪教育网版权所有
故选B.
10. A
【解析】根据不等式的解的定义求解
11.4
【解析】①a(b+c)=ab+ac是等式;
②﹣2<0是用不等号连接的式子,故是不等式;
③x≠5是用不等号连接的式子,故是不等式;
④2a>b+1是用不等号连接的式子,故是不等式;
⑤x2﹣2xy+y2是代数式;
⑥2x﹣3>6是用不等号连接的式子,故是不等式,
故答案是:4.
12.3x+8<2y
【解析】先将x的3倍与8的和表示为3x+8,y的2倍表示为2y,再用“<”将它们表示出来;
解:∵x的3倍与8的和为3x+8,y的2倍是2y,
∴x的3倍与8的和比y的2倍小可表示为:3x+8<2y;
故答案为:3x+8<2y.21cnjy.com
13.<
【解析】如果用一个不等式来表示他们的身高关系,则这个式子可以表示成x<y,
故答案为:<.
14.【解析】由数轴得到m ( http: / / www.21cnjy.com )<n<0,据此判断各式的大小.
解:由数轴可得m<n<0,
(1)两个负数相加,和仍为负数,故m+n<0;
(2)相当于两个异号的数相加,符号由绝对值大的数决定,故m-n<0;
(3)两个负数的积是正数,故m n>0;
(4)正数大于一切负数,故m2>n;
(5)由数轴离原点的距离可得,|m|>|n|.21·世纪*教育网
15.﹣1<k≤3
【解析】根据不大于意思是小于或等于以及大于的意思列出不等式得:
-1<k≤3.
故答案是:-1<k≤3.
【点睛】此题考查了不等式的定义,解题时要读懂题意,抓住关键词语,弄清不等关系,才能把文字语言的不等关系转化为用数学符号表示的不等式.【来源:21·世纪·教育·网】
16.495≤x≤505
【解析】根据题意,可知x应满足的不等式是500-5≤x≤500+5,即495≤x≤505.
故答案为:495≤x≤505.
17.(1)有r≥300;(2)3a+4b≤268;(3)P≥70%.
【解析】试题分析:(1)不小于就是大于等于,用“≥”来表示;
(2)不高于就是等于或低于,用“≤”表示;
(3)不小于就是大于等于,用“≥”来表示;
试题解析:
(1)设炮弹的杀伤半径为r米,则应有r≥300;
(2)设每件上衣为a元,每条长裤是b元,应有3a+4b≤268;
(3)用P表示明天下雨的可能性,则有P≥70%.
【点睛】一般地,用不等号表示不相等关系的式子叫做不等式.解答此类题关键是要识别常见不等号:>,<,≤,≥,≠.2·1·c·n·j·y
18.见解析.
【解析】试题分析:先要了 ( http: / / www.21cnjy.com )解图标的含义,然后根据含义列出不等式即可.图①表示最低时速限制;图②表示车辆过桥洞时限制车高的标志;图③表示车辆过桥时限制车宽的标志;图④车辆过桥时限制车重的标志.21教育网
试题解析:
①设时速为a千米/时,则a≥50;
②设车高为bm,则b≤3.5;
③设车宽为xm,则x≤3;
④设车重为yt,则y≤10.
19.甲、乙之间的距离在3~5 km之间
【解析】试题分析:甲乙都在学校同侧,且 ( http: / / www.21cnjy.com )甲乙与学校在同一直线上时,甲乙两地的距离最小;甲乙在学校两侧,且甲乙与学校在同一直线上时,甲乙两地的距离最大;当甲乙以及学校不在同一直线上时,甲乙的距离在前面两个距离之间.2-1-c-n-j-y
试题解析:①当甲、乙、学校三者在同一直线上时,
若甲、乙在学校的两侧,则甲、乙相距最远为5 km;
若甲、乙在学校的同侧,则甲、乙相距最近为3 km.
②当甲、乙、学校三者不在同一直线上时,
甲、乙之间的距离在3~5 km之间.
点睛:本题考查的是三角形的三边关系,先分别求出三点同线的情况,即最短距离和最长距离两种情况,则d的取值即在这两者之间.【版权所有:21教育】
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
8.1 认识不等式同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.用不等号“<”或“>”表示不等关系的式子,叫做不等式.
2.不等式的解:能使不等式成立的未知数的值 叫做不等式的解.
3.列不等式:应注意“不大于”、“不小于”、“非负数”、“非正数”等关键词,并能准确地用不等号表示.21·cn·jy·com
基础知识和能力拓展精练
一、选择题
1.下列式子:①<y+5;②1>-2;③3m-1≤4;④a+2≠a-2中,不等式有( )
A. 2个 B. 3个 C. 4个 D. 1个
2.x与3的和的一半是负数,用不等式表示为( )
A. x+3>0 B. x+3<0 C. (x+3)<0 D. (x+3)>0
3.“a<b”的反面是( )
A. a≠b B. a>b C. a≥b D. a=b
4.据中央气象台报道,某日上海最高气温是22 ℃,最低气温是11 ℃,则当天上海气温t(℃)的变化范围是( )www.21-cn-jy.com
A. t>22 B. t≤22 C. 11<t<22 D. 11≤t≤22
5.当x=3时,下列不等式成立的是( )
A. x+3>5 B. x+3>6 C. x+3>7 D. x+3<5
6.高钙牛奶的包装盒上注明“每100克内含钙≥150毫克”,它的含义是指( )
A. 每100克内含钙150毫克 B. 每100克内含钙高于150毫克
C. 每100克内含钙不低于150毫克 D. 每100克内含钙不超过150毫克
7.6月8日我县最高气温是29℃,最低气 ( http: / / www.21cnjy.com )温是19℃,则当天我县气温t(℃)的变化范围是( )
A.19≤t≤29 B.t<19 C.t≤19 D.t≥29【来源:21cnj*y.co*m】
8.下列按条件列出的不等式中,正确的是( )
A. a不是负数,则a>0 B. a与3的差不等于1,则a-3<1
C. a是不小于0的数,则a>0 D. a与 b的和是非负数,则a+b≥0
9.5名学生身高两两不同,把他们按从高到低 ( http: / / www.21cnjy.com )排列,设前三名的平均身高为a米,后两名的平均身高为b米.又前两名的平均身高为c米,后三名的平均身高为d米,则( )
A. > B. > C. = D. 以上都不对
10. x=3是下列哪个不等式的解 ( )
A.x+2>4 B.x2-3>6 C.2x-1<3 D.3x+2<10
二、填空题
11.给出下列表达式:①a(b+c)=ab ( http: / / www.21cnjy.com )+ac;②﹣2<0;③x≠5;④2a>b+1;⑤x2﹣2xy+y2;⑥2x﹣3>6,其中不等式的个数是_______.
12.用不等式表示下列关系:x的3倍与8的和比y的2倍小:_______.
13.如图,身高为 ( http: / / www.21cnjy.com )xcm的1号同学与身高为ycm的2号同学站在一起时,如果用一个不等式来表示他们的身高关系,则这个式子可以表示成x_____y(用“>”或“<”填空).
( http: / / www.21cnjy.com )
1号 2号
14.有理数m,n在数轴上如图,用不等号填空.
(1)m+n______0;(2)m-n______0;(3)m n______0;(4)m2______n;(5)|m|______|n|.
15.k的值大于﹣1且不大于3,则用不等式表示 k的取值范围是_____.(使用形如a≤x≤b的类似式子填空.)【出处:21教育名师】
16.按商品质量规定:商店出售的标明5 ( http: / / www.21cnjy.com )00 g的袋装食盐,其实际克数与所标克数相差不能超过5 g.设实际克数为x(g),则x应满足的不等式是_____.21*cnjy*com
三、解答题
17.用适当的符号表示下列关系:
(1)一枚炮弹的杀伤半径不小于300米;
(2)三件上衣与四条长裤的总价钱不高于268元;
(3)明天下雨的可能性不小于70%;
18.在生活中不等关系的应用随处可 ( http: / / www.21cnjy.com )见.如图表示机动车驶入前方道路的最低时速限制.此标志设在高速公路或其他道路限速路段的起点,你会表示这些不等关系吗?
( http: / / www.21cnjy.com )
19.甲地离学校4 km,乙地离学校1 km,记甲、乙两地之间的距离为d(km),求d的取值范围.
参考答案
1.C
【解析】根据不等式的定义:“用不等号表示两个量间的不等关系的式子叫做不等式”分析可知,上述四个式子都是不等式.21教育名师原创作品
故选C.
2.C
【解析】“与3的和的一半是负数”用不等式表示为:
.
故选C.
3.C
【解析】a<b的反面是a=b或a>b,即a≥b.
故选C.
4.D
【解析】气温最高是22℃,则t≤22;
气温最低是11℃,则t≥11.
故气温的变化范围11≤t≤22.
故选D.
5.A
【解析】A项,当x=3时,x+3= ( http: / / www.21cnjy.com )3+3=6>5,所以x+3>5成立;B项,当x=3时,x+3=3+3=6,所以x+3>6不成立;C项,当x=3时,x+3=3+3=6<7,所以;x+3>7不成立;D项,当x=3时,x+3=3+3=6>5,所以x+3<5不成立.21*cnjy*com
故选:A
6.C
【解析】根据≥的含义,“每100克内含钙≥150毫克”,就是“每100克内含钙不低于150毫克”,
故选:C.
7.A
【解析】读懂题意,找到最高气温和最低气温即可 ( http: / / www.21cnjy.com ).
解:因为最低气温是19℃,所以19≤t,最高气温是29℃,t≤29,
则今天气温t(℃)的范围是19≤t≤29.
故选A.
8.D
【解析】根据a不是负数,则a可能是正数和0,即a≥0,故不正确;
根据a与3的差不等于1,可知a-3≠1,故不正确;
根据a是不小于0的数,即可知a≥0,故不正确;
根据非负数的意义,可知a+b≥0,故正确.
故选:D
9.B
【解析】根据把他们按从高到低排列,设前三名的平均身高为a米,后两名的平均身高为b米.又前两名的平均身高为c米,后三名的平均身高为d米,则c>a>d>b,则c-a>0>b-d,得c+d>a+b,得: >.21世纪教育网版权所有
故选B.
10. A
【解析】根据不等式的解的定义求解
11.4
【解析】①a(b+c)=ab+ac是等式;
②﹣2<0是用不等号连接的式子,故是不等式;
③x≠5是用不等号连接的式子,故是不等式;
④2a>b+1是用不等号连接的式子,故是不等式;
⑤x2﹣2xy+y2是代数式;
⑥2x﹣3>6是用不等号连接的式子,故是不等式,
故答案是:4.
12.3x+8<2y
【解析】先将x的3倍与8的和表示为3x+8,y的2倍表示为2y,再用“<”将它们表示出来;
解:∵x的3倍与8的和为3x+8,y的2倍是2y,
∴x的3倍与8的和比y的2倍小可表示为:3x+8<2y;
故答案为:3x+8<2y.21cnjy.com
13.<
【解析】如果用一个不等式来表示他们的身高关系,则这个式子可以表示成x<y,
故答案为:<.
14.【解析】由数轴得到m ( http: / / www.21cnjy.com )<n<0,据此判断各式的大小.
解:由数轴可得m<n<0,
(1)两个负数相加,和仍为负数,故m+n<0;
(2)相当于两个异号的数相加,符号由绝对值大的数决定,故m-n<0;
(3)两个负数的积是正数,故m n>0;
(4)正数大于一切负数,故m2>n;
(5)由数轴离原点的距离可得,|m|>|n|.21·世纪*教育网
15.﹣1<k≤3
【解析】根据不大于意思是小于或等于以及大于的意思列出不等式得:
-1<k≤3.
故答案是:-1<k≤3.
【点睛】此题考查了不等式的定义,解题时要读懂题意,抓住关键词语,弄清不等关系,才能把文字语言的不等关系转化为用数学符号表示的不等式.【来源:21·世纪·教育·网】
16.495≤x≤505
【解析】根据题意,可知x应满足的不等式是500-5≤x≤500+5,即495≤x≤505.
故答案为:495≤x≤505.
17.(1)有r≥300;(2)3a+4b≤268;(3)P≥70%.
【解析】试题分析:(1)不小于就是大于等于,用“≥”来表示;
(2)不高于就是等于或低于,用“≤”表示;
(3)不小于就是大于等于,用“≥”来表示;
试题解析:
(1)设炮弹的杀伤半径为r米,则应有r≥300;
(2)设每件上衣为a元,每条长裤是b元,应有3a+4b≤268;
(3)用P表示明天下雨的可能性,则有P≥70%.
【点睛】一般地,用不等号表示不相等关系的式子叫做不等式.解答此类题关键是要识别常见不等号:>,<,≤,≥,≠.2·1·c·n·j·y
18.见解析.
【解析】试题分析:先要了 ( http: / / www.21cnjy.com )解图标的含义,然后根据含义列出不等式即可.图①表示最低时速限制;图②表示车辆过桥洞时限制车高的标志;图③表示车辆过桥时限制车宽的标志;图④车辆过桥时限制车重的标志.21教育网
试题解析:
①设时速为a千米/时,则a≥50;
②设车高为bm,则b≤3.5;
③设车宽为xm,则x≤3;
④设车重为yt,则y≤10.
19.甲、乙之间的距离在3~5 km之间
【解析】试题分析:甲乙都在学校同侧,且 ( http: / / www.21cnjy.com )甲乙与学校在同一直线上时,甲乙两地的距离最小;甲乙在学校两侧,且甲乙与学校在同一直线上时,甲乙两地的距离最大;当甲乙以及学校不在同一直线上时,甲乙的距离在前面两个距离之间.2-1-c-n-j-y
试题解析:①当甲、乙、学校三者在同一直线上时,
若甲、乙在学校的两侧,则甲、乙相距最远为5 km;
若甲、乙在学校的同侧,则甲、乙相距最近为3 km.
②当甲、乙、学校三者不在同一直线上时,
甲、乙之间的距离在3~5 km之间.
点睛:本题考查的是三角形的三边关系,先分别求出三点同线的情况,即最短距离和最长距离两种情况,则d的取值即在这两者之间.【版权所有:21教育】
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
