18.1 平行四边形的性质(2)同步练习
文档属性
| 名称 | 18.1 平行四边形的性质(2)同步练习 |  | |
| 格式 | doc | ||
| 文件大小 | 475.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-16 15:57:37 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
18.1 平行四边形的性质(2)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.有两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的对边平行且相等对角相等.
3.平行线之间的距离处处相等.
基础知识和能力拓展精练
一、选择题
1.如图,在平行四边形ABCD中,∠ABC的平分线BE交AD于E,∠AEB=25°,则∠A的大小为( )
A. 100° B. 120° C. 130° D. 150°
2.如图,在△ABC中,∠BAC=45°,AB=AC=8,P为AB 边上一动点,以PA,PC为边作□PAQC,则对角线PQ长度的最小值为( )
A. 6 B. 8 C. 2 D. 4
3.如图,□ABCD的对角线AC的长为10 cm,∠CAB=30°,AB的长为6 cm,则□ABCD的面积为( )
A. 60cm2 B. 30cm2 C. 20cm2 D. 16cm2
4.如图所示,直线a∥b,A是直线a上的一个定点,线段BC在直线b上移动,那么在移动过程中△ABC的面积( )
A. 变大 B. 变小 C. 不变 D. 无法确定
5.如图,在□ABCD中,点M为CD的中点,且DC=2AD,则AM与BM的夹角的度数为( )
A. 100° B. 95° C. 90° D. 85°
6.在平行四边形ABCD中,∠A的平分线交DC于E,若∠DEA=30°,则∠B=( )
A100° B.120° C.135° D.150°
7.平行四边形的周长为24,相邻两边的差为2,则平行四边形的各边长为( )
A. 4,4,8,8 B. 5,5,7,7 C. 5.5,5.5,6.5,6.5 D. 3,3,9,9
8.如图,在 ABCD中,对角线AC的垂直平分线分别交AD、BC于点E、F,连接CE,若 ABCD的周长为20,则△CED的周长为( )
A. 5 B. 10 C. 15 D. 20
9.如图,□ABCD中,EF过对角线的交点O,AB=4,AD=3,OF=1,则四边形BCEF的周长为( )
A. 8 B. 9 C. 12 D. 13
10.如图,□ABCD的周长为20cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
A. 4cm B. 6cm C. 8cm D. 10cm
二、填空题
11.如图,在□ABCD中,对角线AC,BD交于点O,若DO=1.5 cm,AB=5 cm,BC=4 cm,则□ABCD的面积为________cm2.
12.平行四边形ABCD中,若∠A∶∠B=1∶3,那么∠A=________,∠B=________,∠C=________,∠D=________.
13.在平行四边形ABCD中,∠A的平分线把BC边分成长度是3和5的两部分,则平行四边形ABCD周长是_____________.
14.如图,在 ABCD中,∠C=40°,过点D作CB的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为____.
15.如图,在□ABCD中,AE⊥BC于E,AF⊥CD于F,AE=4,AF=6,AB+AD=20,则□ABCD的面积为_____.
16.在平行四边形中, , ,过点作垂直直线于点, ,再过点作垂直于直线于点,则__________.
三、解答题
17.在平行四边形ABCD中, ∠A+∠C=160°,求∠A,∠C,∠B,∠D的度数.
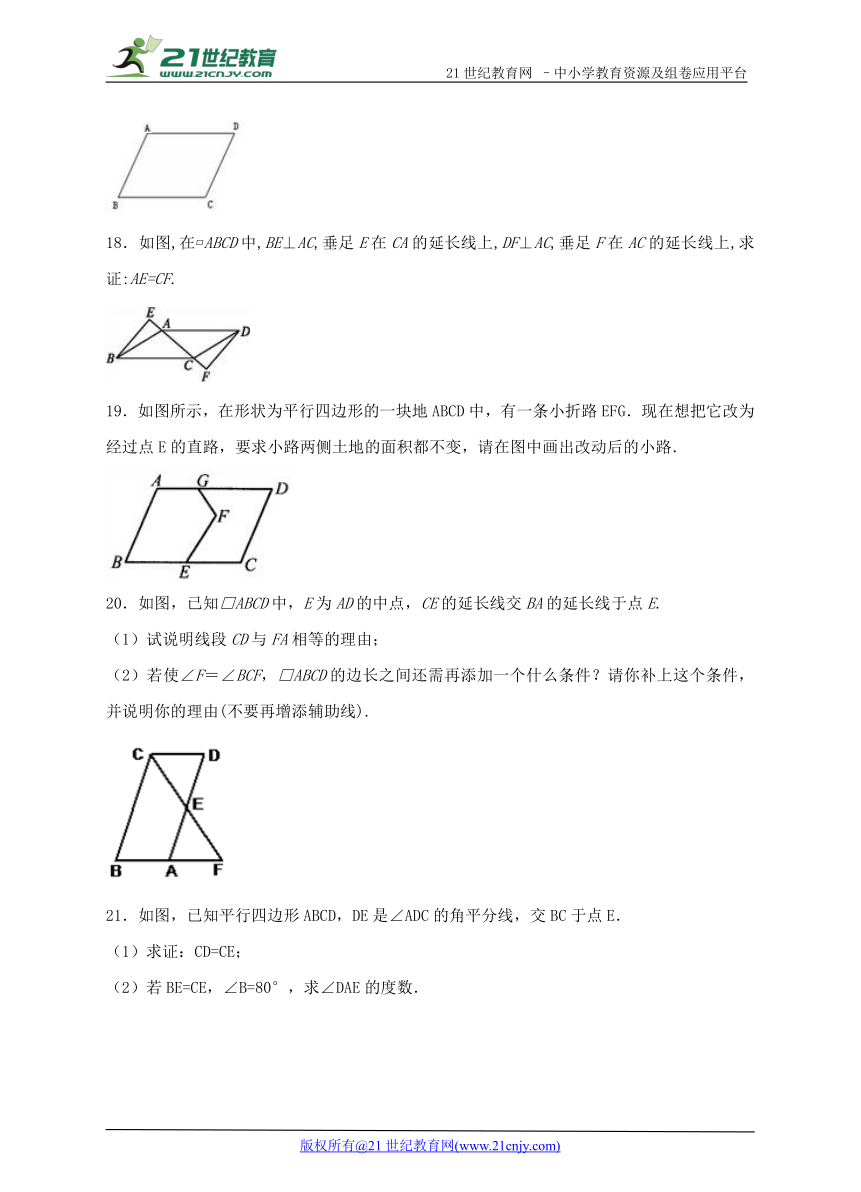
18.如图,在 ABCD中,BE⊥AC,垂足E在CA的延长线上,DF⊥AC,垂足F在AC的延长线上,求证:AE=CF.
19.如图所示,在形状为平行四边形的一块地ABCD中,有一条小折路EFG.现在想把它改为经过点E的直路,要求小路两侧土地的面积都不变,请在图中画出改动后的小路.
20.如图,已知□ABCD中,E为AD的中点,CE的延长线交BA的延长线于点E.
(1)试说明线段CD与FA相等的理由;
(2)若使∠F=∠BCF,□ABCD的边长之间还需再添加一个什么条件?请你补上这个条件,并说明你的理由(不要再增添辅助线).
21.如图,已知平行四边形ABCD,DE是∠ADC的角平分线,交BC于点E.
(1)求证:CD=CE;
(2)若BE=CE,∠B=80°,求∠DAE的度数.
22.已知在□ABCD中,AEBC于E,DF平分ADC 交线段AE于F.
(1)如图1,若AE=AD,ADC=60, 请直接写出线段CD与AF+BE之间所满足的等量关系;
(2)如图2, 若AE=AD,你在(1)中得到的结论是否仍然成立, 若成立,对你的结论加以证明, 若不成立, 请说明理由;
参考答案
1.C
【解析】解:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠AEB=∠CBE.
∵∠ABC的平分线交AD于E,∴∠ABE=∠CBE=∠AEB=25°,∴∠A=180°-∠ABE-∠AEB=130°.故选C.
2.D
【解析】试题解析:∵四边形APCQ是平行四边形,
∴AO=CO,OP=OQ,
∵PQ最短也就是PO最短,
∴过O作OP′⊥AB与P′,
∴△AP′O是等腰直角三角形,
∴PQ的最小值
故选D.
3.B
【解析】试题解析:过点C作CH⊥AB,交AB延长线于点H.
故选B.
4.C
【解析】试题解析:如图,∵a∥b,
∴a,b之间的距离是固定的,
而△ABC的高和这个距离相等,
所以△ABC的高、底边都是固定的,
所以它的面积不变.
故选C.
5.C
【解析】试题解析: 中,
∴DC∥AB,AD∥BC,
∴∠DAB+∠CBA=180°,∠BAM=∠DMA,
∵点M为CD的中点,且DC=2AD,
∴DM=AD,
∴∠DMA=∠DAM,
∴∠DAM=∠BAM,
同理∠ABM=∠CBM,
即:
∴∠AMB=180°-90°=90°.
故选C.
6.B
【解析】根据平行四边形的性质邻角互补来解答.∠A的平分线交DC于E,若∠DEA=30°,所以∠A的度数应为60°.∠A与∠B互补,所以∠B=120°.所以选B.
7.B
【解析】平行四边形的对边相等,所以两邻边的和为周长的一半.周长为24,则两邻边的和为12.又因为相邻的两边相差2,则可计算出较长的一边为7,较短的一边长为5.所以选B.
8.B
【解析】∵对角线AC的垂直平分线分别交AD、AC于点E. O,
∴AE=CE,
∵ ABCD的周长为20,
∴AD+DC=10,
∴=4,
∴△CDE的周长为CD+ED+CE=CD+AD=10,
故选:B.
9.B
【解析】解:∵四边形ABCD是平行四边形(已知),∴OA=OC(平行四边形的对角线相互平分),AB∥CD(平行四边形的对边相互平行),∴∠DCO=∠BAC(两直线平行,内错角相等).
在△AFO和△CEO中,∵∠OAF=∠OCE, AO=CO,∠AOF=∠COE,∴△AFO≌△CEO(ASA),∴OF=OE,CE=AF(全等三角形的对应边相等).
又∵AD=BC(平行四边形的对边相等),AB=4,AD=3,OF=1,∴四边形BCEF的周长为:BC+EC+OE+OF+BF=AD+AF+2OF+BF=AD+AB+2OF=9.故选B.
10.D
【解析】试题解析:∵四边形ABCD是平行四边形,
∵ ABCD的周长为20cm,
∴AD+CD=10cm,
的周长为
故选D.
11.12
【解析】试题解析:∵四边形ABCD是平行四边形,
∴BD=2DO=2×1.5=3(cm),CD=AB=5cm,
∵BC=4cm,
即DB⊥BC,
故答案为:12.
12. 45° 135° 45° 135°
【解析】根据平行四边形的性质:对角相等,邻角互补来解答.∠A与∠B是邻角,度数和应为180°.又从题干中得知,∠A∶∠B=1∶3,所以不难算出∠A=45°,∠B=135°.又因为平行四边形对角相等,所以,∠C=∠A=45°,∠D=∠B=135°.
故答案: (1). 45° (2). 135° (3). 45° (4). 135°.
13.22或26
【解析】在平行四边形ABCD中,AD∥BC,则∠DAE=∠AEB.
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE,BC=BE+EC,
①当BE=3,EC=5时,
平行四边形ABCD的周长为:2(AB+AD)=2(3+3+5)=22.
②当BE=5,EC=3时,
平行四边形ABCD的周长为:2(AB+AD)=2(5+5+3)=26.
故答案为:22或26.
14.50°
【解析】由题意得∠C=40°,∠F=90°,所以∠CDF=50°,因为DC ,所以∠BEF=50°.
15.48
【解析】设BC=x,∵AB+AD=20, 所以BC+CD=20,∴CD=20-x,
∵□ABCD的面积=BC AE=CD AF,∴4x=6(20-x),解得x=12,
∴□ABCD的面积=BC AE=12×4=48,故答案为:48.
16.4.5或13.5
【解析】解:如图,∵BC=5,AE⊥BC,AE=,∴平行四边形ABCD的面积为:BC AE=5×=.∵四边形ABCD是平行四边形,∴AB=CD=4,BC=AD=5.
①由平行四边形面积公式得:BC×AE=CD×AF=,则AF=.
在Rt△ABE和Rt△ADF中,由勾股定理得:AB2=AE2+BE2,把AB=4,AE=代入求出BE=2,同理DF=<4,即F在线段DC上(如图1),∴CE=5﹣2=3,CF=4﹣=,即CE+CF=3+=4.5;
②如图:∵AB=4,AE=,在△ABE中,由勾股定理得:BE===2,同理DF=.
则CE=BC+BE=5+2=7,CF=CD+DF=4+=6.5,∴CE+CF=7+6.5=13.5;
故答案为:4.5或13.5.
点睛:本题考查了平行四边形性质,勾股定理的应用,主要培养学生的理解能力和计算能力,注意:要分类讨论.
17.∠A=80°,∠C=80°,∠B=100°,∠D=100°
【解析】【试题分析】
根据平行四边形的性质:对角相等、邻角互补来解答.
【试题解析】
在平行四边形ABCD中,∠A=∠C,
又∵∠A+∠C=160°
∴∠A=∠C=80°
∵在平行四边形ABCD中AD∥CB
∴∠A+∠B=180°
∴∠B=∠D=180°
∠A=∠C=180°-80°=100°.
【方法点睛】本题考查平行四边形的性质.掌握平行四边形对角相等、邻角互补的性质,就能解答本题.
18.见解析
【解析】由平行四边形的性质得出AB∥CD,AB=CD,由平行线的性质得出得出∠BAC=∠DCA,证出∠EAB=∠FCD,根据垂直得出∠BEA=∠DFC=90°,由AAS证明△BEA≌△DFC,即可得出结论.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAC=∠DCA,
∴180° ∠BAC=180° ∠DCA,
即∠EAB=∠FCD,
∵BE⊥AC,DF⊥AC,
∴∠BEA=∠DFC=90°,
在△BEA和△DFC中,
,
∴△BEA≌△DFC(AAS),
∴AE=CF.
19.见解析
【解析】试题分析:首先连接EG,过点F作EG的平行线交BC于点N,根据三角形面积关系,只要证明△EIN面积等于△GIF面积,即可解决问题.
试题解析:解:连接EG,过点F作EG的平行线交BC于点N.连接GN,GN就是所取直的小路.
证明:设GN交FE于点I.
∵EG∥FN,∴△GNF的面积等于△EFN的面积,(同底等高).
把两个三角形面积都减去△FIN面积,所以△EIN面积等于△GIF面积,即小路两侧土地面积都不变.
点睛:此题考查的是等积变换,能根据题意作出辅助线,构造出面积相等的三角形是解答此题的关键.
20.见解析
【解析】试题分析:(1)根据平行四边形的性质,-就可证明CD∥AB,∠CDA=∠DAF,又已知DE=AE,∠CED=∠AEF,符合全等三角形的判定中的ASA,即证△CDE≌△AEF,所以CD=AF.
(2)在第(1)问的基础上,若使∠F=∠BCF,逆推就必须BC=BF,继而推出BC=2BA,即为所求.
试题解析:(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB.
又∵CE的延长线交BA的延长线于点F,
∴∠CDA=∠DAF.
∵E是AD中点,
∴DE=AE.
∵∠CED=∠AEF,
∴△CDE≌△AEF.
∴CD=AF.
(2)要使∠F=∠BCF,需平行四边形ABCD的边长之间是2倍的关系,即BC=2AB,
证明:∵由(1)知,△CED≌△FEA,
∴CD=AF.
又∵四边形ABCD是平行四边形,
∴CD=AB.
∴AB=AF,即BF=2AB.
∵BC=2AB.
∴BF=BC,
∴∠F=∠BCF.
21.(1)证明见解析;(2)∠DAE=50°.
【解析】试题分析:(1)根据DE是∠ADC的角平分线得到∠1=∠2,再根据平行四边形的性质得到∠1=∠3,所以∠2=∠3,根据等角对等边即可得证;
(2)先根据BE=CE结合CD=CE得到△ABE是等腰三角形,求出∠BAE的度数,再根据平行四边形邻角互补得到∠BAD=100°,所以∠DAE可求.
(1)证明:如图,在平行四边形ABCD中,
∵AD∥BC
∴∠1=∠3
又∵∠1=∠2,
∴∠2=∠3,
∴CD=CE;
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
又∵CD=CE,BE=CE,
∴AB=BE,
∴∠BAE=∠BEA.
∵∠B=80°,
∴∠BAE=50°,
∴∠DAE=180°﹣50°﹣80°=50°.
点睛:本题主要考查平行四边形的性质,根据平行四边形的性质中对边平行,以及DE是∠ADC的平分线,证明△DEC是等腰三角形,以类似的方法也可以求出∠DAE的角度.
22.(1)CD=AF+BE.(2)(1)中的结论仍然成立.证明见解析.
【解析】试题分析:(1)、利用截长补短法可以得出线段之间的关系;(2)、延长EA到G,使得AG=BE,连结DG,根据平行四边形的性质得出△ABE和△DAG全等,从而得出DG=AB,根据角度之间的关系得出DG=GF,即CD=GF=AF+AG=AF+BE得出答案.
试题解析:(1)、CD=AF+BE.
(2)、解:(1)中的结论仍然成立.
证明:延长EA到G,使得AG=BE,连结DG,
∵ 四边形ABCD是平行四边形, ∴ AB=CD,AB∥CD,AD=BC,
∵ AE⊥BC于点E, ∴ ∠AEB=∠AEC=90, ∴∠AEB=∠DAG=90, ∴ ∠DAG=90,
∵ AE=AD, ∴ △ABE≌△DAG, ∴∠1=∠2, DG=AB, ∴∠GFD=90-∠3,
∵ DF平分∠ADC, ∴∠3=∠4,
∴∠GDF=∠2+∠3=∠1+∠4=180-∠FAD-∠3=90-∠3, ∴∠GDF=∠GFD,∴ DG=GF.
∴ CD=GF=AF+AG= AF + BE, 即 CD = AF +BE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
18.1 平行四边形的性质(2)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.有两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的对边平行且相等对角相等.
3.平行线之间的距离处处相等.
基础知识和能力拓展精练
一、选择题
1.如图,在平行四边形ABCD中,∠ABC的平分线BE交AD于E,∠AEB=25°,则∠A的大小为( )
A. 100° B. 120° C. 130° D. 150°
2.如图,在△ABC中,∠BAC=45°,AB=AC=8,P为AB 边上一动点,以PA,PC为边作□PAQC,则对角线PQ长度的最小值为( )
A. 6 B. 8 C. 2 D. 4
3.如图,□ABCD的对角线AC的长为10 cm,∠CAB=30°,AB的长为6 cm,则□ABCD的面积为( )
A. 60cm2 B. 30cm2 C. 20cm2 D. 16cm2
4.如图所示,直线a∥b,A是直线a上的一个定点,线段BC在直线b上移动,那么在移动过程中△ABC的面积( )
A. 变大 B. 变小 C. 不变 D. 无法确定
5.如图,在□ABCD中,点M为CD的中点,且DC=2AD,则AM与BM的夹角的度数为( )
A. 100° B. 95° C. 90° D. 85°
6.在平行四边形ABCD中,∠A的平分线交DC于E,若∠DEA=30°,则∠B=( )
A100° B.120° C.135° D.150°
7.平行四边形的周长为24,相邻两边的差为2,则平行四边形的各边长为( )
A. 4,4,8,8 B. 5,5,7,7 C. 5.5,5.5,6.5,6.5 D. 3,3,9,9
8.如图,在 ABCD中,对角线AC的垂直平分线分别交AD、BC于点E、F,连接CE,若 ABCD的周长为20,则△CED的周长为( )
A. 5 B. 10 C. 15 D. 20
9.如图,□ABCD中,EF过对角线的交点O,AB=4,AD=3,OF=1,则四边形BCEF的周长为( )
A. 8 B. 9 C. 12 D. 13
10.如图,□ABCD的周长为20cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
A. 4cm B. 6cm C. 8cm D. 10cm
二、填空题
11.如图,在□ABCD中,对角线AC,BD交于点O,若DO=1.5 cm,AB=5 cm,BC=4 cm,则□ABCD的面积为________cm2.
12.平行四边形ABCD中,若∠A∶∠B=1∶3,那么∠A=________,∠B=________,∠C=________,∠D=________.
13.在平行四边形ABCD中,∠A的平分线把BC边分成长度是3和5的两部分,则平行四边形ABCD周长是_____________.
14.如图,在 ABCD中,∠C=40°,过点D作CB的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为____.
15.如图,在□ABCD中,AE⊥BC于E,AF⊥CD于F,AE=4,AF=6,AB+AD=20,则□ABCD的面积为_____.
16.在平行四边形中, , ,过点作垂直直线于点, ,再过点作垂直于直线于点,则__________.
三、解答题
17.在平行四边形ABCD中, ∠A+∠C=160°,求∠A,∠C,∠B,∠D的度数.
18.如图,在 ABCD中,BE⊥AC,垂足E在CA的延长线上,DF⊥AC,垂足F在AC的延长线上,求证:AE=CF.
19.如图所示,在形状为平行四边形的一块地ABCD中,有一条小折路EFG.现在想把它改为经过点E的直路,要求小路两侧土地的面积都不变,请在图中画出改动后的小路.
20.如图,已知□ABCD中,E为AD的中点,CE的延长线交BA的延长线于点E.
(1)试说明线段CD与FA相等的理由;
(2)若使∠F=∠BCF,□ABCD的边长之间还需再添加一个什么条件?请你补上这个条件,并说明你的理由(不要再增添辅助线).
21.如图,已知平行四边形ABCD,DE是∠ADC的角平分线,交BC于点E.
(1)求证:CD=CE;
(2)若BE=CE,∠B=80°,求∠DAE的度数.
22.已知在□ABCD中,AEBC于E,DF平分ADC 交线段AE于F.
(1)如图1,若AE=AD,ADC=60, 请直接写出线段CD与AF+BE之间所满足的等量关系;
(2)如图2, 若AE=AD,你在(1)中得到的结论是否仍然成立, 若成立,对你的结论加以证明, 若不成立, 请说明理由;
参考答案
1.C
【解析】解:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠AEB=∠CBE.
∵∠ABC的平分线交AD于E,∴∠ABE=∠CBE=∠AEB=25°,∴∠A=180°-∠ABE-∠AEB=130°.故选C.
2.D
【解析】试题解析:∵四边形APCQ是平行四边形,
∴AO=CO,OP=OQ,
∵PQ最短也就是PO最短,
∴过O作OP′⊥AB与P′,
∴△AP′O是等腰直角三角形,
∴PQ的最小值
故选D.
3.B
【解析】试题解析:过点C作CH⊥AB,交AB延长线于点H.
故选B.
4.C
【解析】试题解析:如图,∵a∥b,
∴a,b之间的距离是固定的,
而△ABC的高和这个距离相等,
所以△ABC的高、底边都是固定的,
所以它的面积不变.
故选C.
5.C
【解析】试题解析: 中,
∴DC∥AB,AD∥BC,
∴∠DAB+∠CBA=180°,∠BAM=∠DMA,
∵点M为CD的中点,且DC=2AD,
∴DM=AD,
∴∠DMA=∠DAM,
∴∠DAM=∠BAM,
同理∠ABM=∠CBM,
即:
∴∠AMB=180°-90°=90°.
故选C.
6.B
【解析】根据平行四边形的性质邻角互补来解答.∠A的平分线交DC于E,若∠DEA=30°,所以∠A的度数应为60°.∠A与∠B互补,所以∠B=120°.所以选B.
7.B
【解析】平行四边形的对边相等,所以两邻边的和为周长的一半.周长为24,则两邻边的和为12.又因为相邻的两边相差2,则可计算出较长的一边为7,较短的一边长为5.所以选B.
8.B
【解析】∵对角线AC的垂直平分线分别交AD、AC于点E. O,
∴AE=CE,
∵ ABCD的周长为20,
∴AD+DC=10,
∴=4,
∴△CDE的周长为CD+ED+CE=CD+AD=10,
故选:B.
9.B
【解析】解:∵四边形ABCD是平行四边形(已知),∴OA=OC(平行四边形的对角线相互平分),AB∥CD(平行四边形的对边相互平行),∴∠DCO=∠BAC(两直线平行,内错角相等).
在△AFO和△CEO中,∵∠OAF=∠OCE, AO=CO,∠AOF=∠COE,∴△AFO≌△CEO(ASA),∴OF=OE,CE=AF(全等三角形的对应边相等).
又∵AD=BC(平行四边形的对边相等),AB=4,AD=3,OF=1,∴四边形BCEF的周长为:BC+EC+OE+OF+BF=AD+AF+2OF+BF=AD+AB+2OF=9.故选B.
10.D
【解析】试题解析:∵四边形ABCD是平行四边形,
∵ ABCD的周长为20cm,
∴AD+CD=10cm,
的周长为
故选D.
11.12
【解析】试题解析:∵四边形ABCD是平行四边形,
∴BD=2DO=2×1.5=3(cm),CD=AB=5cm,
∵BC=4cm,
即DB⊥BC,
故答案为:12.
12. 45° 135° 45° 135°
【解析】根据平行四边形的性质:对角相等,邻角互补来解答.∠A与∠B是邻角,度数和应为180°.又从题干中得知,∠A∶∠B=1∶3,所以不难算出∠A=45°,∠B=135°.又因为平行四边形对角相等,所以,∠C=∠A=45°,∠D=∠B=135°.
故答案: (1). 45° (2). 135° (3). 45° (4). 135°.
13.22或26
【解析】在平行四边形ABCD中,AD∥BC,则∠DAE=∠AEB.
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE,BC=BE+EC,
①当BE=3,EC=5时,
平行四边形ABCD的周长为:2(AB+AD)=2(3+3+5)=22.
②当BE=5,EC=3时,
平行四边形ABCD的周长为:2(AB+AD)=2(5+5+3)=26.
故答案为:22或26.
14.50°
【解析】由题意得∠C=40°,∠F=90°,所以∠CDF=50°,因为DC ,所以∠BEF=50°.
15.48
【解析】设BC=x,∵AB+AD=20, 所以BC+CD=20,∴CD=20-x,
∵□ABCD的面积=BC AE=CD AF,∴4x=6(20-x),解得x=12,
∴□ABCD的面积=BC AE=12×4=48,故答案为:48.
16.4.5或13.5
【解析】解:如图,∵BC=5,AE⊥BC,AE=,∴平行四边形ABCD的面积为:BC AE=5×=.∵四边形ABCD是平行四边形,∴AB=CD=4,BC=AD=5.
①由平行四边形面积公式得:BC×AE=CD×AF=,则AF=.
在Rt△ABE和Rt△ADF中,由勾股定理得:AB2=AE2+BE2,把AB=4,AE=代入求出BE=2,同理DF=<4,即F在线段DC上(如图1),∴CE=5﹣2=3,CF=4﹣=,即CE+CF=3+=4.5;
②如图:∵AB=4,AE=,在△ABE中,由勾股定理得:BE===2,同理DF=.
则CE=BC+BE=5+2=7,CF=CD+DF=4+=6.5,∴CE+CF=7+6.5=13.5;
故答案为:4.5或13.5.
点睛:本题考查了平行四边形性质,勾股定理的应用,主要培养学生的理解能力和计算能力,注意:要分类讨论.
17.∠A=80°,∠C=80°,∠B=100°,∠D=100°
【解析】【试题分析】
根据平行四边形的性质:对角相等、邻角互补来解答.
【试题解析】
在平行四边形ABCD中,∠A=∠C,
又∵∠A+∠C=160°
∴∠A=∠C=80°
∵在平行四边形ABCD中AD∥CB
∴∠A+∠B=180°
∴∠B=∠D=180°
∠A=∠C=180°-80°=100°.
【方法点睛】本题考查平行四边形的性质.掌握平行四边形对角相等、邻角互补的性质,就能解答本题.
18.见解析
【解析】由平行四边形的性质得出AB∥CD,AB=CD,由平行线的性质得出得出∠BAC=∠DCA,证出∠EAB=∠FCD,根据垂直得出∠BEA=∠DFC=90°,由AAS证明△BEA≌△DFC,即可得出结论.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAC=∠DCA,
∴180° ∠BAC=180° ∠DCA,
即∠EAB=∠FCD,
∵BE⊥AC,DF⊥AC,
∴∠BEA=∠DFC=90°,
在△BEA和△DFC中,
,
∴△BEA≌△DFC(AAS),
∴AE=CF.
19.见解析
【解析】试题分析:首先连接EG,过点F作EG的平行线交BC于点N,根据三角形面积关系,只要证明△EIN面积等于△GIF面积,即可解决问题.
试题解析:解:连接EG,过点F作EG的平行线交BC于点N.连接GN,GN就是所取直的小路.
证明:设GN交FE于点I.
∵EG∥FN,∴△GNF的面积等于△EFN的面积,(同底等高).
把两个三角形面积都减去△FIN面积,所以△EIN面积等于△GIF面积,即小路两侧土地面积都不变.
点睛:此题考查的是等积变换,能根据题意作出辅助线,构造出面积相等的三角形是解答此题的关键.
20.见解析
【解析】试题分析:(1)根据平行四边形的性质,-就可证明CD∥AB,∠CDA=∠DAF,又已知DE=AE,∠CED=∠AEF,符合全等三角形的判定中的ASA,即证△CDE≌△AEF,所以CD=AF.
(2)在第(1)问的基础上,若使∠F=∠BCF,逆推就必须BC=BF,继而推出BC=2BA,即为所求.
试题解析:(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB.
又∵CE的延长线交BA的延长线于点F,
∴∠CDA=∠DAF.
∵E是AD中点,
∴DE=AE.
∵∠CED=∠AEF,
∴△CDE≌△AEF.
∴CD=AF.
(2)要使∠F=∠BCF,需平行四边形ABCD的边长之间是2倍的关系,即BC=2AB,
证明:∵由(1)知,△CED≌△FEA,
∴CD=AF.
又∵四边形ABCD是平行四边形,
∴CD=AB.
∴AB=AF,即BF=2AB.
∵BC=2AB.
∴BF=BC,
∴∠F=∠BCF.
21.(1)证明见解析;(2)∠DAE=50°.
【解析】试题分析:(1)根据DE是∠ADC的角平分线得到∠1=∠2,再根据平行四边形的性质得到∠1=∠3,所以∠2=∠3,根据等角对等边即可得证;
(2)先根据BE=CE结合CD=CE得到△ABE是等腰三角形,求出∠BAE的度数,再根据平行四边形邻角互补得到∠BAD=100°,所以∠DAE可求.
(1)证明:如图,在平行四边形ABCD中,
∵AD∥BC
∴∠1=∠3
又∵∠1=∠2,
∴∠2=∠3,
∴CD=CE;
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
又∵CD=CE,BE=CE,
∴AB=BE,
∴∠BAE=∠BEA.
∵∠B=80°,
∴∠BAE=50°,
∴∠DAE=180°﹣50°﹣80°=50°.
点睛:本题主要考查平行四边形的性质,根据平行四边形的性质中对边平行,以及DE是∠ADC的平分线,证明△DEC是等腰三角形,以类似的方法也可以求出∠DAE的角度.
22.(1)CD=AF+BE.(2)(1)中的结论仍然成立.证明见解析.
【解析】试题分析:(1)、利用截长补短法可以得出线段之间的关系;(2)、延长EA到G,使得AG=BE,连结DG,根据平行四边形的性质得出△ABE和△DAG全等,从而得出DG=AB,根据角度之间的关系得出DG=GF,即CD=GF=AF+AG=AF+BE得出答案.
试题解析:(1)、CD=AF+BE.
(2)、解:(1)中的结论仍然成立.
证明:延长EA到G,使得AG=BE,连结DG,
∵ 四边形ABCD是平行四边形, ∴ AB=CD,AB∥CD,AD=BC,
∵ AE⊥BC于点E, ∴ ∠AEB=∠AEC=90, ∴∠AEB=∠DAG=90, ∴ ∠DAG=90,
∵ AE=AD, ∴ △ABE≌△DAG, ∴∠1=∠2, DG=AB, ∴∠GFD=90-∠3,
∵ DF平分∠ADC, ∴∠3=∠4,
∴∠GDF=∠2+∠3=∠1+∠4=180-∠FAD-∠3=90-∠3, ∴∠GDF=∠GFD,∴ DG=GF.
∴ CD=GF=AF+AG= AF + BE, 即 CD = AF +BE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
