苏科版九年级下册数学《第7章锐角函数》单元检测卷(含答案)
文档属性
| 名称 | 苏科版九年级下册数学《第7章锐角函数》单元检测卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 239.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-16 22:41:50 | ||
图片预览




文档简介
第7章锐角函数单元检测卷 姓名:__________ 班级:__________
题号
一
二
三
总分
评分
?
?
?
?
一、选择题(共11小题;每小题3分,共33分)
1.的值为(??? )
A. B. C. D.1
2.如图,在△ABC中,BC=10,∠B=60°,∠C=45°,则点A到BC的距离是( ??)
A.?10﹣5 ??????????????????????????B.?5+5 ??????????????????????????C.?15﹣5 ??????????????????????????D.?15﹣10
3.如图,延长Rt△ABC斜边AB到D点,使BD=AB,连接CD,若cot∠BCD=3,则tanA=(? ?)
A.???????????????????????????????????????????B.?1??????????????????????????????????????????C.???????????????????????????????????????????D.?
4. 在Rt△ABC中,∠C=90°,AB=4,AC=1,则cosB的值为(?? )
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
5. 如图,已知在 中, , , ,则 的值是(?? )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
6. 某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为(?? )
A.?3.5sin29°米?????????????????B.?3.5cos29°米?????????????????C.?3.5tan29°米?????????????????D.?米
7. 如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则(?? )
A.?x﹣y2=3?????????????????????????B.?2x﹣y2=9?????????????????????????C.?3x﹣y2=15?????????????????????????D.?4x﹣y2=21
8. 如图,在平面直角坐标系中,点A的坐标为(﹣1, ),以原点O为中心,将点A顺时针旋转150°得到点A′,则点A′的坐标为(?? )
A.?(0,﹣2)????????????????????B.?(1,﹣ )????????????????????C.?(2,0)????????????????????D.?( ,﹣1)
9. 如图,菱形ABCD的边长为2,∠A=60°,点P和点Q分别从点B和点C出发,沿射线BC向右运动,且速度相同,过点Q作QH⊥BD,垂足为H,连接PH,设点P运动的距离为x(0<x≤2),△BPH的面积为S,则能反映S与x之间的函数关系的图象大致为(?? )
A.?????????????B.?????????????C.?????????????D.?
10. 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为F,连结DF,下列四个结论:①△AEF∽△CAB;②tan∠CAD= ;③DF=DC;④CF=2AF,正确的是(?? )
A.?①②③????????????????????????????????B.?②③④????????????????????????????????C.?①③④????????????????????????????????D.?①②④
11. 如图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5,若点P是⊙O上的一点,在△ABP中,PB=AB,则PA的长为(?? )
A.?5??????????????????????????????????????B.???????????????????????????????????????C.?5 ??????????????????????????????????????D.?5
二、填空题(共10题;共30分)
12.一等腰三角形的两边长分别为4cm和6cm,则其底角的余弦值为________.
13.计算:2cos60°﹣tan45°=________.
14.如图,△ABC中,DE是BC的垂直平分线,DE交AC于点E,连接BE.若BE=9,BC=12,则cosC=________.
15. 如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么cos∠EFC的值是________.
16. △ABC中,AB=12,AC= ,∠B=30°,则△ABC的面积是________.
17. 在Rt△ABC中,∠C=90°,AB=2,BC= ,则sin =________.
18. 在半径为1的⊙O中,弦AB、AC的长分别为1和 ,则∠BAC的度数为________.
19. 如图,Rt△ABC中,∠C=90°,BC=15,tanA= ,则AB=________.
20. 如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC= ,反比例函数y= 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于________.
21. (﹣ )﹣3﹣2cos45°+(3.14﹣π)0+ =________.
三、解答题(共5题;共37分)
22.如图,锐角△ABC中,AB=10cm,BC=9cm,△ABC的面积为27cm2 . 求tanB的值.
23.已知α为锐角且cosα是方程2x2﹣7x+3=0的一个根,求 的值.
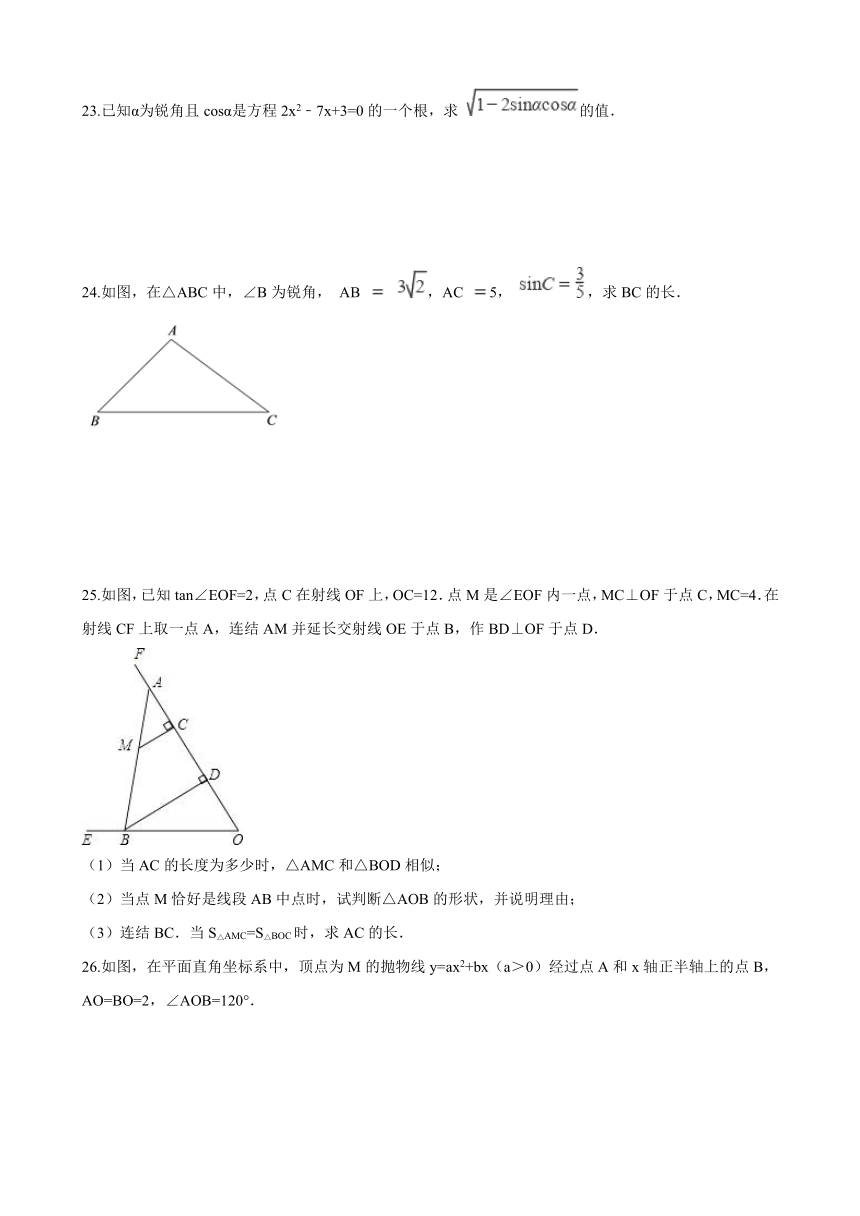
24.如图,在△ABC中,∠B为锐角, AB ? ,AC 5, ,求BC的长.
25.如图,已知tan∠EOF=2,点C在射线OF上,OC=12.点M是∠EOF内一点,MC⊥OF于点C,MC=4.在射线CF上取一点A,连结AM并延长交射线OE于点B,作BD⊥OF于点D.
(1)当AC的长度为多少时,△AMC和△BOD相似;
(2)当点M恰好是线段AB中点时,试判断△AOB的形状,并说明理由;
(3)连结BC.当S△AMC=S△BOC时,求AC的长.
26.如图,在平面直角坐标系中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=BO=2,∠AOB=120°.
(1)求a,b的值;
(2)连结OM,求∠AOM的大小.
参考答案
一、选择题
C C A A A A B D A C D
二、填空题
12. 或
13. 0
14.
15.
16. 21 或15
17.
18. 15°或105°
19. 17
20. ﹣24
21. ﹣7+
三、解答题
22. 解:过点A作AH⊥BC于H, ∵S△ABC=27, ∴ , ∴AH=6, ∵AB=10, ∴BH= = =8, ∴tanB= = = .
23. 解:∵cosα是方程2x2﹣7x+3=0的一个根, ∴由求根公式有,cosα= , ∴cosα= (cosα=3不符合题意,舍去), ∵sin2α+cos2α=1, ∴sin2α=1﹣( )2= , ∴sinα= , ∴ = = =sinα﹣cosα=
24. 解:如图,作AD⊥BC于点D, ∴ ∠ADB=∠ADC=90°. ∵ AC=5, , ∴ . ∴ 在Rt△ACD中, . ∵ AB ? , ∴ 在Rt△ABD中, . ∴ .
25. (1)解:∵∠MCA=∠BDO=Rt∠, ∴△AMC和△BOD中,C与D是对应点, ∴△AMC和△BOD相似时分两种情况: ①当△AMC∽△BOD时, =tan∠EOF=2, ∵MC=4, ∴ =2, 解得AC=8; ②当△AMC∽△OBD时, =tan∠EOF=2, ∵MC=4, ∴ =2, 解得AC=2. 故当AC的长度为2或8时,△AMC和△BOD相似 (2)解:△ABO为直角三角形.理由如下: ∵MC∥BD, ∴△AMC∽△ABD, ∴ ,∠AMC=∠ABD, ∵M为AB中点, ∴C为AD中点,BD=2MC=8. ∵tan∠EOF=2, ∴OD=4, ∴CD=OC﹣OD=8, ∴AC=CD=8. 在△AMC与△BOD中, , ∴△AMC≌△BOD(SAS), ∴∠CAM=∠DBO, ∴∠ABO=∠ABD+∠DBO=∠AMC+∠CAM=90°, ∴△ABO为直角三角形 (3)解:连结BC, 设OD=a,则BD=2a. ∵S△AMC=S△BOC , S△AMC= AC MC=2AC,S△BOC= OC BD=12a, ∴2AC=12a, ∴AC=6a. ∵△AMC∽△ABD, ∴ ,即 , 解得a1=3,a2=﹣ (舍去), ∴AC=6×3=18.
26. (1)解:如图,过点A作AE⊥y轴于点E, ∵AO=OB=2,∠AOB=120°, ∴∠AOE=30°, ∴AE=1,EO= , ∴A点坐标为:(﹣1, ),B点坐标为:(2,0), 将两点代入y=ax2+bx得: , 解得: . ∴a= ,b=﹣ (2)解:由(1)可知:抛物线的表达式为:y= x2﹣ x; 过点M作MF⊥OB于点F, ∵y= x2﹣ x= (x2﹣2x)= (x﹣1)2﹣ , ∴M点坐标为:(1,﹣ ), ∴tan∠FOM= = , ∴∠FOM=30°, ∴∠AOM=30°+120°=150°
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
