18.2 平行四边形的判定(1)同步练习
文档属性
| 名称 | 18.2 平行四边形的判定(1)同步练习 |  | |
| 格式 | doc | ||
| 文件大小 | 423.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-18 10:59:20 | ||
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
18.2 平行四边形的判定(1)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.平行四边形的判定方法:
(1)定义法:两组对边分别平行的四边形是平行四边形 ;
(2)判定定理1:两组对边分别相等的四边形是平行四边形 .
2.平行四边形的定义既是判定方法又是性质,要学会灵活运用;判定定理应用的常规思路是:由边相等得平行四边形,进而利用平行四边形的性质解决问题.
基础知识和能力拓展精练
一、选择题
1.如图,AB=CD=EF,且△ACE≌△BDF,则图中平行四边形的个数为( )
A. 1 B. 2 C. 3 D. 4
2.如图,将平行四边形ABCD沿翻折,使点恰好落在上的点处,则下列结论不一定成立的是( )
A. B. C. D.
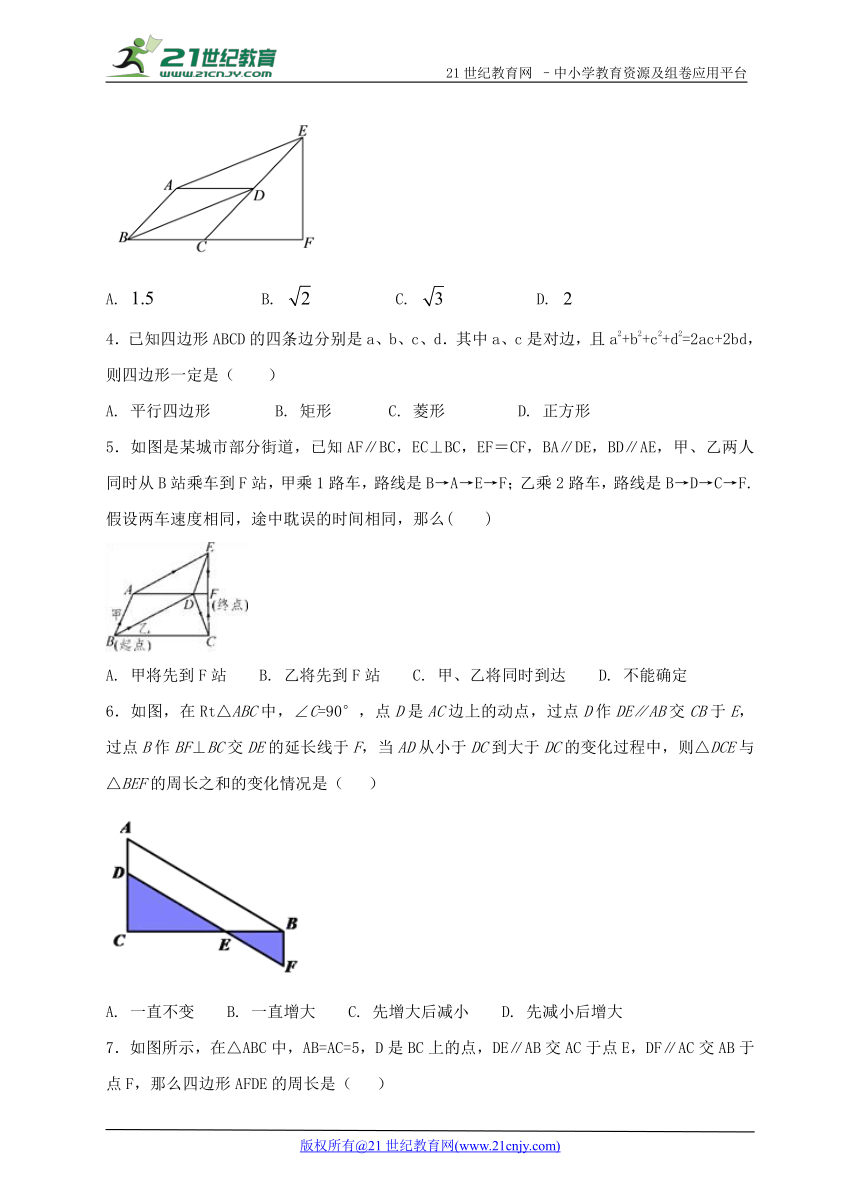
3.如图,平行四边形ABCD中,∠ABC=450,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,AB=1,则EF的长是( )
A. B. C. D.
4.已知四边形ABCD的四条边分别是a、b、c、d.其中a、c是对边,且a2+b2+c2+d2=2ac+2bd,则四边形一定是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
5.如图是某城市部分街道,已知AF∥BC,EC⊥BC,EF=CF,BA∥DE,BD∥AE,甲、乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F;乙乘2路车,路线是B→D→C→F.假设两车速度相同,途中耽误的时间相同,那么( )
A. 甲将先到F站 B. 乙将先到F站 C. 甲、乙将同时到达 D. 不能确定
6.如图,在Rt△ABC中,∠C=90°,点D是AC边上的动点,过点D作DE∥AB交CB于E,过点B作BF⊥BC交DE的延长线于F,当AD从小于DC到大于DC的变化过程中,则△DCE与△BEF的周长之和的变化情况是( )
A. 一直不变 B. 一直增大 C. 先增大后减小 D. 先减小后增大
7.如图所示,在△ABC中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是( )
A. 5 B. 10 C. 15 D. 20
二、填空题
8.若四边形ABCD的边AB=CD,BC=DA,则这个四边形是___________,理由是__________.
9.如图,AB∥EG,EF∥BC,AC∥FG,图中有_______个平行四边形,它们分别是____________.
10.如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,点D,E分别是AB,AC的中点,点G,F在BC边上(均不与端点重合),DG∥EF.将△BDG绕点D顺时针旋转180°,将△CEF绕点E逆时针旋转180°,拼成四边形MGFN,则四边形MGFN周长l的取值范围是___________.
11.如图,四边形ABCD是平行四边形,∠ABC=70°,BE平分∠ABC且交AD于点E,DF∥BE且交BC于点F,则∠1的度数为 .
三、解答题
12.如图所示,在△ABC中,∠ACB=90°点E是AB的中点,连接CE,过点E作ED⊥BC于点D,在DE的延长线上取一点F,使AF=CE,求证四边形ACEF是平行四边形.
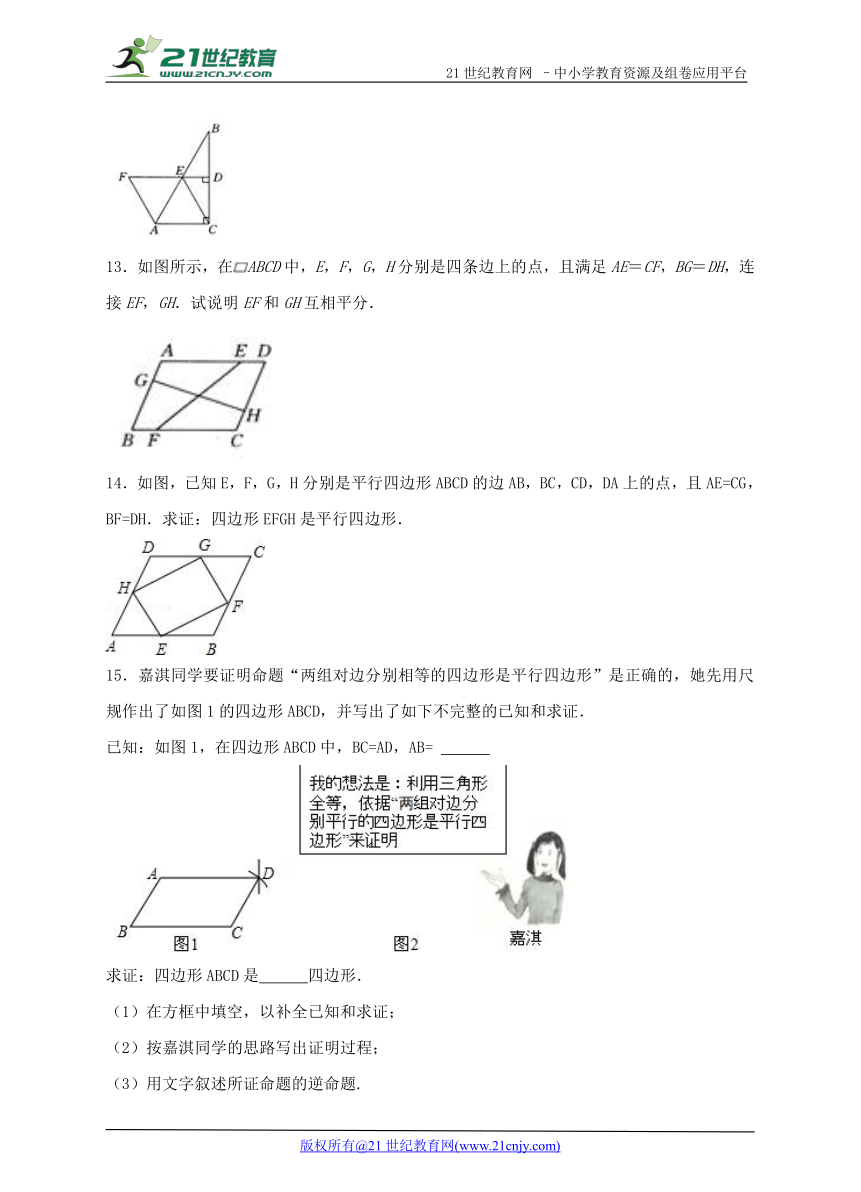
13.如图所示,在ABCD中,E,F,G,H分别是四条边上的点,且满足AE=CF,BG=DH,连接EF,GH.试说明EF和GH互相平分.
14.如图,已知E,F,G,H分别是平行四边形ABCD的边AB,BC,CD,DA上的点,且AE=CG,BF=DH.求证:四边形EFGH是平行四边形.
15.嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,AB=
求证:四边形ABCD是 四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的思路写出证明过程;
(3)用文字叙述所证命题的逆命题.
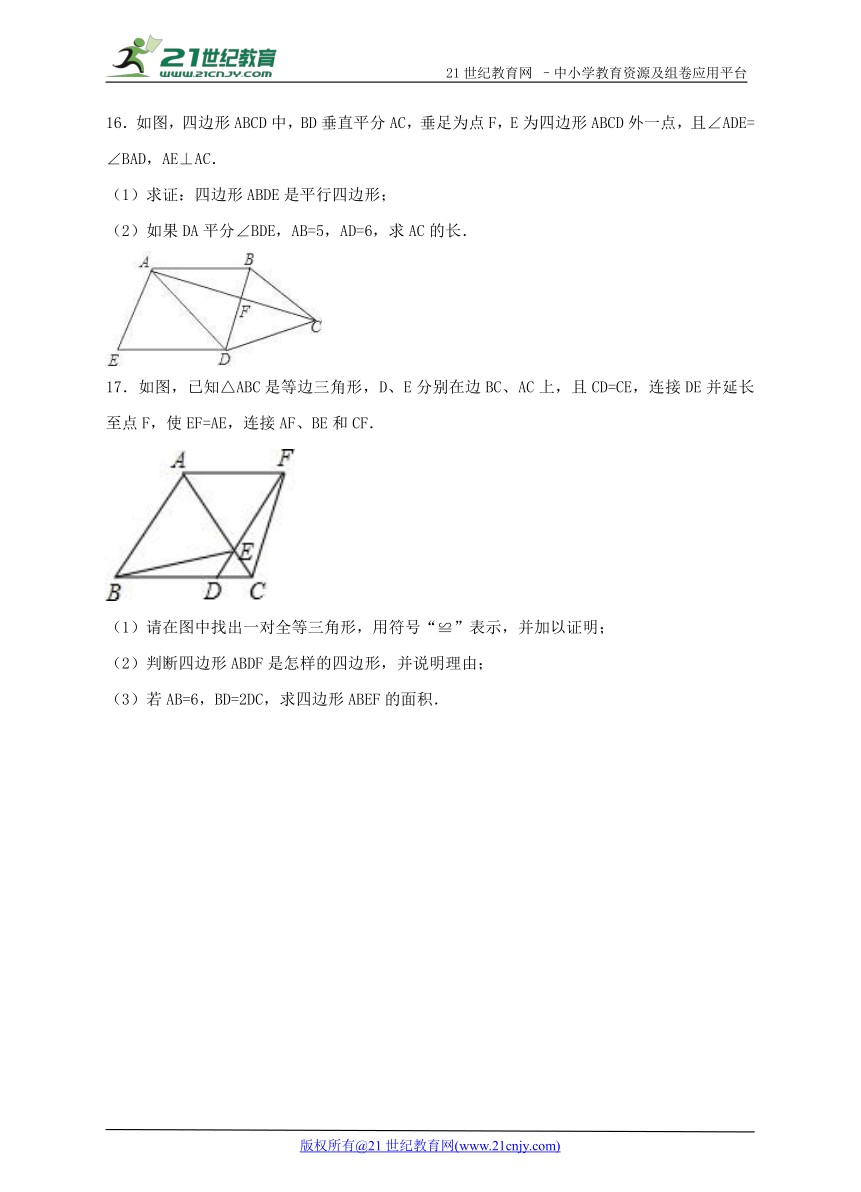
16.如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC.
(1)求证:四边形ABDE是平行四边形;
(2)如果DA平分∠BDE,AB=5,AD=6,求AC的长.
17.如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.
(1)请在图中找出一对全等三角形,用符号“≌”表示,并加以证明;
(2)判断四边形ABDF是怎样的四边形,并说明理由;
(3)若AB=6,BD=2DC,求四边形ABEF的面积.
参考答案
1.C
【解析】试题解析:∵△ACE≌△BDF,
∴AC=BD、CE=DF、AE=BF,
∵AB=CD=EF,
∴平行四边形有 ACDB、 CEFD、 AEFB三个,
故选C.
点睛:利用两组对边分别平行的四边形是平行四边形判定平行四边形即可;
2.C
【解析】试题分析:根据题意可得:四边形ABEF为平行四边形,则AB=EF,AF=BE,根据折叠的性质可得:AF=AB=EF,故本题选C.
3.B
【解析】∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB=1,
∴∠ECF=∠ABC=45°,
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴DE=AB=1
∴CE=CD+DE=2,
∵EF⊥BC,∠ECF=45°,
∴△CEF是等腰直角三角形.
∴EF=CF,EF2+CF2=CE2=4,
∴2EF2=4,
∴EF=.
故选B.
4.A
【解析】因为a2+b2+c2+d2=2ac+2bd,所以a2-2ac+c2+b2-2bd+d2=0,
所以(a-c)2+(b-d)2=0,所以a-c=0,b-d=0,所以a=c,b=d.
所以四边形ABCD是平行四边形.
故选A.
5.C
【解析】∵BA∥DE,BD∥AE
∴四边形ABDE是平行四边形,
∴AE=BD,AB=DE,
∵AF∥BC,EC⊥BC,EF=CF,
∴AF是EC的垂直平分线,
∴DE=CD,
∴BA+AE+EF=BD+CD+EF,
∵两车速度相同,途中耽误的时间相同,
∴甲乙两个人同时到达.
故选:C.
6.A
【解析】∵AC⊥BC,BF⊥BC, ∴AC∥BF.
又∵DE∥AB, ∴四边形ABFD是平行四边形,
∴BF=AD,DF=DE+EF=AB,
∴△DCE与△BEF的周长之和等于△ABC的周长,
∴△DCE与△BEF的周长之和一直不变.
故选A.
7.B
【解析】试题分析:根据平行四边形的性质,找出对应相等的边,利用等腰三角形的性质把四边形周长转化为已知的长度去解题.∵DE∥AB,DF∥AC,则四边形AFDE是平行四边形,∠B=∠EDC,∠FDB=∠C
∵AB=AC,∴∠B=∠C, ∴∠B=∠FDB,∠C=∠EDF ∴BF=FD,DE=EC,
所以: AFDE的周长等于AB+AC=10.
考点:(1)、平行四边形的性质;(2)、等腰三角形的性质;(3)、平行四边形的判定.
8. 平行四边形 两组对边分别相等的四边形是平行四边形
【解析】试题解析:若四边形ABCD的边AB=CD,BC=DA,则这个四边形是平行四边形,理由是两组对边分别相等的四边形是平行四边形,
故答案为:平行,两组对边分别相等的四边形是平行四边形.
9. 3 □ABCE,□ABGC,□AFBC
【解析】试题解析:图中共有3个平行四边形,它们分别是
理由如下:
∵AB∥EG,EF∥BC,AC∥FG,
∴AB∥EC,EA∥BC,
∴四边形ABCE是平行四边形;
同理可证,四边形ABGC是平行四边形;
四边形AFBC是平行四边形.
故答案为:3,
10.≤l<13
【解析】如图,连接DE,作AH⊥BC于H.
在Rt△ABC中, ∵∠BAC=90°AB=4,AC=3,,
,
,
,
, ,
, ,
,
∴四边形DGEF是平行四边形,
,
根据题意,,
∴四边形MNFG是平行四边形,
∴当MG=NF=AH时,可得四边形MNFG周长的最小值= ,
当G与B重合时可得周长的最大值为13,
∵G不与B重合,
.
点睛:本题考查了旋转的性质,勾股定理,平行四边形的判定与性质,根据图形找出四边形MNFG周长的最小值和最大值时的界点是解答本题的关键.
11.35°.
【解析】
试题分析:∵四边形ABCD是平行四边形,∴DE∥BF,∵DF∥BE,∴四边形EBFD是平行四边形,
∴∠EBF=∠EDF,∴∠CDF=∠ABR,∵∠ABC=70°,BE平分∠ABC且交AD于E,
∴∠ABE=35°,∴∠CDF=35°,∴∠1=70°﹣35°=35°,
故答案为:35°.
考点: 平行四边形的性质.
12.答案见解析
【解析】试题分析:要证明四边形ACEF是平行四边形,需求证CE∥AF,由已知易得△BEC,△AEF是等腰三角形,则∠1=∠2,∠3=∠F,又∠2=∠3,得到∠1=∠F,故CE∥AF,由此即可得到结论.
试题解析:证明:∵点E为AB中点,∴AE=EB.又∵∠ACB=90°,∴CE=AE=EB.又∵AF=CE,∴AF=AE,∴∠3=∠F.又∵EB=EC,ED⊥BC,∴∠1=∠2(三线合一).又∵∠2=∠3,∴∠1=∠F,∴CE∥AF,∴四边形ACEF是平行四边形.
点睛:平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.
13.答案见解析
【解析】试题分析:如图,连接EG,GF,FH,HE,证明四边形EGFH是平行四边形,问题即可解决.
试题解析:解:连接EG,GF,FH,HE.如图,∵四边形ABCD为平行四边形,∴∠B=∠D,AD=BC.又∵AE=CF,∴AD-AE=BC-CF,即DE=BF.又∵DH=BG,∴△BFG≌△DEH(SAS),∴GF=EH,同理GE=FH,∴四边形EGFH平行四边形,∴EF和GH互相平分.
14.见解析
【解析】试题分析:易证得△AEH≌△CGF,从而证得对应边EH=FG.同理可证:HG=EF,根据两组对边分别相等的四边形是平行四边形得证.
试题解析:证明:在平行四边形ABCD中,∠A=∠C,AD=BC.∵BF=DH,∴AH=CF.∵AE=CG,∠A=∠C,AH=CF,∴△AEH≌△CGF(SAS),∴EH=FG(全等三角形的对应边相等).
同理可证:HG=EF,∴四边形EFGH是平行四边形(两组对边分别相等的四边形是平行四边形).
15.(1)见解析;(2)见解析
【解析】试题分析:(1)命题的题设为“两组对边分别相等的四边形”,结论是“是平行四边形”,即可得到结论;
(2)连接BD,利用SSS定理证明△ABD≌△CDB可得∠ADB=∠DBC,∠ABD=∠CDB,进而可得AB∥CD,AD∥CB,根据两组对边分别平行的四边形是平行四边形可得四边形ABCD是平行四边形;
(3)把命题“两组对边分别相等的四边形是平行四边形”的题设和结论对换可得平行四边形两组对边分别相等.
试题解析:解:(1)已知:如图1,在四边形ABCD中,BC=AD,AB=CD.
求证:四边形ABCD是平行四边形.
(2)证明:连接BD.
在△ABD和△CDB中,∵AB=CD,AD=BC,BD=DB,∴△ABD≌△CDB(SSS),
∴∠ADB=∠DBC,∠ABD=∠CDB,∴AB∥CD,AD∥CB,∴四边形ABCD是平行四边形;
(3)用文字叙述所证命题的逆命题为:
平行四边形两组对边分别相等.
16.(1)证明见试题解析;(2)9.6.
【解析】试题分析:(1)根据已知和角平分线的定义证明∠ADE=∠BAD,得到DE∥AB,又AE∥BD,根据两组对边分别平行的四边形是平行四边形证明即可;
(2)设BF=x,根据勾股定理求出x的值,再根据勾股定理求出AF,根据AC=2AF得到答案.
试题解析:(1)∵AE⊥AC,BD垂直平分AC,
∴AE∥BD,
∵∠ADE=∠BAD,
∴DE∥AB,
∴四边形ABDE是平行四边形;
(2)∵DA平分∠BDE,
∴∠BAD=∠ADB,
∴AB=BD=5,
设BF=x,
则52-x2=62-(5-x)2,
解得,x=,
∴AF=,
∴AC=2AF=.
考点:平行四边形的判定与性质.
17.(1)见解析;(2)平行四边形;(3)
【解析】试题分析:(1)从图上及已知条件容易看出△BDE≌△FEC,△BCE≌△FDC,△ABE≌△ACF.判定两个三角形全等时,必须有边的参与,所以此题的关键是找出相等的边.
(2)由(1)的结论容易证明AB∥DF,BD∥AF,两组对边分别平行的四边形是平行四边形.
(3)EF∥AB,EF≠AB,四边形ABEF是梯形,只要求出此梯形的面积即可.
试题解析:解:(1)△BDE≌△FEC或△BCE≌△FDC或△ABE≌△ACF.
(选证一)△BDE≌△FEC.
证明:∵△ABC是等边三角形,∴BC=AC,∠ACB=60°.
∵CD=CE,∴△EDC是等边三角形,∴DE=EC,∠CDE=∠DEC=60°,∴∠BDE=∠FEC=120°.
又∵EF=AE,∴BD=FE,∴△BDE≌△FEC.
(选证二)△BCE≌△FDC.
证明:∵△ABC是等边三角形,∴BC=AC,∠ACB=60°.
又∵CD=CE,∴△EDC是等边三角形,∴∠BCE=∠FDC=60°,DE=CE.
∵EF=AE,∴EF+DE=AE+CE,∴FD=AC=BC,∴△BCE≌△FDC.
(选证三)△ABE≌△ACF.
证明:∵△ABC是等边三角形,∴AB=AC,∠ACB=∠BAC=60°.
∵CD=CE,∴△EDC是等边三角形,∴∠AEF=∠CED=60°.
∵EF=AE,△AEF是等边三角形,∴AE=AF,∠EAF=60°,∴△ABE≌△ACF.
(2)由(1)知,△ABC、△EDC、△AEF都是等边三角形,∴∠CDE=∠ABC=∠EFA=60°,∴AB∥DF,BD∥AF,∴四边形ABDF是平行四边形.
(3)由(2)知,四边形ABDF是平行四边形,∴EF∥AB,EF≠AB,∴四边形ABEF是梯形.
过E作EG⊥AB于G,则EG=,∴
.
点睛:此题考查了全等三角形的判定,平行四边形的判定,及梯形面积的求解,用到的知识点比较多,较复杂.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
18.2 平行四边形的判定(1)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.平行四边形的判定方法:
(1)定义法:两组对边分别平行的四边形是平行四边形 ;
(2)判定定理1:两组对边分别相等的四边形是平行四边形 .
2.平行四边形的定义既是判定方法又是性质,要学会灵活运用;判定定理应用的常规思路是:由边相等得平行四边形,进而利用平行四边形的性质解决问题.
基础知识和能力拓展精练
一、选择题
1.如图,AB=CD=EF,且△ACE≌△BDF,则图中平行四边形的个数为( )
A. 1 B. 2 C. 3 D. 4
2.如图,将平行四边形ABCD沿翻折,使点恰好落在上的点处,则下列结论不一定成立的是( )
A. B. C. D.
3.如图,平行四边形ABCD中,∠ABC=450,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,AB=1,则EF的长是( )
A. B. C. D.
4.已知四边形ABCD的四条边分别是a、b、c、d.其中a、c是对边,且a2+b2+c2+d2=2ac+2bd,则四边形一定是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
5.如图是某城市部分街道,已知AF∥BC,EC⊥BC,EF=CF,BA∥DE,BD∥AE,甲、乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F;乙乘2路车,路线是B→D→C→F.假设两车速度相同,途中耽误的时间相同,那么( )
A. 甲将先到F站 B. 乙将先到F站 C. 甲、乙将同时到达 D. 不能确定
6.如图,在Rt△ABC中,∠C=90°,点D是AC边上的动点,过点D作DE∥AB交CB于E,过点B作BF⊥BC交DE的延长线于F,当AD从小于DC到大于DC的变化过程中,则△DCE与△BEF的周长之和的变化情况是( )
A. 一直不变 B. 一直增大 C. 先增大后减小 D. 先减小后增大
7.如图所示,在△ABC中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是( )
A. 5 B. 10 C. 15 D. 20
二、填空题
8.若四边形ABCD的边AB=CD,BC=DA,则这个四边形是___________,理由是__________.
9.如图,AB∥EG,EF∥BC,AC∥FG,图中有_______个平行四边形,它们分别是____________.
10.如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,点D,E分别是AB,AC的中点,点G,F在BC边上(均不与端点重合),DG∥EF.将△BDG绕点D顺时针旋转180°,将△CEF绕点E逆时针旋转180°,拼成四边形MGFN,则四边形MGFN周长l的取值范围是___________.
11.如图,四边形ABCD是平行四边形,∠ABC=70°,BE平分∠ABC且交AD于点E,DF∥BE且交BC于点F,则∠1的度数为 .
三、解答题
12.如图所示,在△ABC中,∠ACB=90°点E是AB的中点,连接CE,过点E作ED⊥BC于点D,在DE的延长线上取一点F,使AF=CE,求证四边形ACEF是平行四边形.
13.如图所示,在ABCD中,E,F,G,H分别是四条边上的点,且满足AE=CF,BG=DH,连接EF,GH.试说明EF和GH互相平分.
14.如图,已知E,F,G,H分别是平行四边形ABCD的边AB,BC,CD,DA上的点,且AE=CG,BF=DH.求证:四边形EFGH是平行四边形.
15.嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,AB=
求证:四边形ABCD是 四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的思路写出证明过程;
(3)用文字叙述所证命题的逆命题.
16.如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC.
(1)求证:四边形ABDE是平行四边形;
(2)如果DA平分∠BDE,AB=5,AD=6,求AC的长.
17.如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.
(1)请在图中找出一对全等三角形,用符号“≌”表示,并加以证明;
(2)判断四边形ABDF是怎样的四边形,并说明理由;
(3)若AB=6,BD=2DC,求四边形ABEF的面积.
参考答案
1.C
【解析】试题解析:∵△ACE≌△BDF,
∴AC=BD、CE=DF、AE=BF,
∵AB=CD=EF,
∴平行四边形有 ACDB、 CEFD、 AEFB三个,
故选C.
点睛:利用两组对边分别平行的四边形是平行四边形判定平行四边形即可;
2.C
【解析】试题分析:根据题意可得:四边形ABEF为平行四边形,则AB=EF,AF=BE,根据折叠的性质可得:AF=AB=EF,故本题选C.
3.B
【解析】∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB=1,
∴∠ECF=∠ABC=45°,
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴DE=AB=1
∴CE=CD+DE=2,
∵EF⊥BC,∠ECF=45°,
∴△CEF是等腰直角三角形.
∴EF=CF,EF2+CF2=CE2=4,
∴2EF2=4,
∴EF=.
故选B.
4.A
【解析】因为a2+b2+c2+d2=2ac+2bd,所以a2-2ac+c2+b2-2bd+d2=0,
所以(a-c)2+(b-d)2=0,所以a-c=0,b-d=0,所以a=c,b=d.
所以四边形ABCD是平行四边形.
故选A.
5.C
【解析】∵BA∥DE,BD∥AE
∴四边形ABDE是平行四边形,
∴AE=BD,AB=DE,
∵AF∥BC,EC⊥BC,EF=CF,
∴AF是EC的垂直平分线,
∴DE=CD,
∴BA+AE+EF=BD+CD+EF,
∵两车速度相同,途中耽误的时间相同,
∴甲乙两个人同时到达.
故选:C.
6.A
【解析】∵AC⊥BC,BF⊥BC, ∴AC∥BF.
又∵DE∥AB, ∴四边形ABFD是平行四边形,
∴BF=AD,DF=DE+EF=AB,
∴△DCE与△BEF的周长之和等于△ABC的周长,
∴△DCE与△BEF的周长之和一直不变.
故选A.
7.B
【解析】试题分析:根据平行四边形的性质,找出对应相等的边,利用等腰三角形的性质把四边形周长转化为已知的长度去解题.∵DE∥AB,DF∥AC,则四边形AFDE是平行四边形,∠B=∠EDC,∠FDB=∠C
∵AB=AC,∴∠B=∠C, ∴∠B=∠FDB,∠C=∠EDF ∴BF=FD,DE=EC,
所以: AFDE的周长等于AB+AC=10.
考点:(1)、平行四边形的性质;(2)、等腰三角形的性质;(3)、平行四边形的判定.
8. 平行四边形 两组对边分别相等的四边形是平行四边形
【解析】试题解析:若四边形ABCD的边AB=CD,BC=DA,则这个四边形是平行四边形,理由是两组对边分别相等的四边形是平行四边形,
故答案为:平行,两组对边分别相等的四边形是平行四边形.
9. 3 □ABCE,□ABGC,□AFBC
【解析】试题解析:图中共有3个平行四边形,它们分别是
理由如下:
∵AB∥EG,EF∥BC,AC∥FG,
∴AB∥EC,EA∥BC,
∴四边形ABCE是平行四边形;
同理可证,四边形ABGC是平行四边形;
四边形AFBC是平行四边形.
故答案为:3,
10.≤l<13
【解析】如图,连接DE,作AH⊥BC于H.
在Rt△ABC中, ∵∠BAC=90°AB=4,AC=3,,
,
,
,
, ,
, ,
,
∴四边形DGEF是平行四边形,
,
根据题意,,
∴四边形MNFG是平行四边形,
∴当MG=NF=AH时,可得四边形MNFG周长的最小值= ,
当G与B重合时可得周长的最大值为13,
∵G不与B重合,
.
点睛:本题考查了旋转的性质,勾股定理,平行四边形的判定与性质,根据图形找出四边形MNFG周长的最小值和最大值时的界点是解答本题的关键.
11.35°.
【解析】
试题分析:∵四边形ABCD是平行四边形,∴DE∥BF,∵DF∥BE,∴四边形EBFD是平行四边形,
∴∠EBF=∠EDF,∴∠CDF=∠ABR,∵∠ABC=70°,BE平分∠ABC且交AD于E,
∴∠ABE=35°,∴∠CDF=35°,∴∠1=70°﹣35°=35°,
故答案为:35°.
考点: 平行四边形的性质.
12.答案见解析
【解析】试题分析:要证明四边形ACEF是平行四边形,需求证CE∥AF,由已知易得△BEC,△AEF是等腰三角形,则∠1=∠2,∠3=∠F,又∠2=∠3,得到∠1=∠F,故CE∥AF,由此即可得到结论.
试题解析:证明:∵点E为AB中点,∴AE=EB.又∵∠ACB=90°,∴CE=AE=EB.又∵AF=CE,∴AF=AE,∴∠3=∠F.又∵EB=EC,ED⊥BC,∴∠1=∠2(三线合一).又∵∠2=∠3,∴∠1=∠F,∴CE∥AF,∴四边形ACEF是平行四边形.
点睛:平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.
13.答案见解析
【解析】试题分析:如图,连接EG,GF,FH,HE,证明四边形EGFH是平行四边形,问题即可解决.
试题解析:解:连接EG,GF,FH,HE.如图,∵四边形ABCD为平行四边形,∴∠B=∠D,AD=BC.又∵AE=CF,∴AD-AE=BC-CF,即DE=BF.又∵DH=BG,∴△BFG≌△DEH(SAS),∴GF=EH,同理GE=FH,∴四边形EGFH平行四边形,∴EF和GH互相平分.
14.见解析
【解析】试题分析:易证得△AEH≌△CGF,从而证得对应边EH=FG.同理可证:HG=EF,根据两组对边分别相等的四边形是平行四边形得证.
试题解析:证明:在平行四边形ABCD中,∠A=∠C,AD=BC.∵BF=DH,∴AH=CF.∵AE=CG,∠A=∠C,AH=CF,∴△AEH≌△CGF(SAS),∴EH=FG(全等三角形的对应边相等).
同理可证:HG=EF,∴四边形EFGH是平行四边形(两组对边分别相等的四边形是平行四边形).
15.(1)见解析;(2)见解析
【解析】试题分析:(1)命题的题设为“两组对边分别相等的四边形”,结论是“是平行四边形”,即可得到结论;
(2)连接BD,利用SSS定理证明△ABD≌△CDB可得∠ADB=∠DBC,∠ABD=∠CDB,进而可得AB∥CD,AD∥CB,根据两组对边分别平行的四边形是平行四边形可得四边形ABCD是平行四边形;
(3)把命题“两组对边分别相等的四边形是平行四边形”的题设和结论对换可得平行四边形两组对边分别相等.
试题解析:解:(1)已知:如图1,在四边形ABCD中,BC=AD,AB=CD.
求证:四边形ABCD是平行四边形.
(2)证明:连接BD.
在△ABD和△CDB中,∵AB=CD,AD=BC,BD=DB,∴△ABD≌△CDB(SSS),
∴∠ADB=∠DBC,∠ABD=∠CDB,∴AB∥CD,AD∥CB,∴四边形ABCD是平行四边形;
(3)用文字叙述所证命题的逆命题为:
平行四边形两组对边分别相等.
16.(1)证明见试题解析;(2)9.6.
【解析】试题分析:(1)根据已知和角平分线的定义证明∠ADE=∠BAD,得到DE∥AB,又AE∥BD,根据两组对边分别平行的四边形是平行四边形证明即可;
(2)设BF=x,根据勾股定理求出x的值,再根据勾股定理求出AF,根据AC=2AF得到答案.
试题解析:(1)∵AE⊥AC,BD垂直平分AC,
∴AE∥BD,
∵∠ADE=∠BAD,
∴DE∥AB,
∴四边形ABDE是平行四边形;
(2)∵DA平分∠BDE,
∴∠BAD=∠ADB,
∴AB=BD=5,
设BF=x,
则52-x2=62-(5-x)2,
解得,x=,
∴AF=,
∴AC=2AF=.
考点:平行四边形的判定与性质.
17.(1)见解析;(2)平行四边形;(3)
【解析】试题分析:(1)从图上及已知条件容易看出△BDE≌△FEC,△BCE≌△FDC,△ABE≌△ACF.判定两个三角形全等时,必须有边的参与,所以此题的关键是找出相等的边.
(2)由(1)的结论容易证明AB∥DF,BD∥AF,两组对边分别平行的四边形是平行四边形.
(3)EF∥AB,EF≠AB,四边形ABEF是梯形,只要求出此梯形的面积即可.
试题解析:解:(1)△BDE≌△FEC或△BCE≌△FDC或△ABE≌△ACF.
(选证一)△BDE≌△FEC.
证明:∵△ABC是等边三角形,∴BC=AC,∠ACB=60°.
∵CD=CE,∴△EDC是等边三角形,∴DE=EC,∠CDE=∠DEC=60°,∴∠BDE=∠FEC=120°.
又∵EF=AE,∴BD=FE,∴△BDE≌△FEC.
(选证二)△BCE≌△FDC.
证明:∵△ABC是等边三角形,∴BC=AC,∠ACB=60°.
又∵CD=CE,∴△EDC是等边三角形,∴∠BCE=∠FDC=60°,DE=CE.
∵EF=AE,∴EF+DE=AE+CE,∴FD=AC=BC,∴△BCE≌△FDC.
(选证三)△ABE≌△ACF.
证明:∵△ABC是等边三角形,∴AB=AC,∠ACB=∠BAC=60°.
∵CD=CE,∴△EDC是等边三角形,∴∠AEF=∠CED=60°.
∵EF=AE,△AEF是等边三角形,∴AE=AF,∠EAF=60°,∴△ABE≌△ACF.
(2)由(1)知,△ABC、△EDC、△AEF都是等边三角形,∴∠CDE=∠ABC=∠EFA=60°,∴AB∥DF,BD∥AF,∴四边形ABDF是平行四边形.
(3)由(2)知,四边形ABDF是平行四边形,∴EF∥AB,EF≠AB,∴四边形ABEF是梯形.
过E作EG⊥AB于G,则EG=,∴
.
点睛:此题考查了全等三角形的判定,平行四边形的判定,及梯形面积的求解,用到的知识点比较多,较复杂.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
