人教版八年级数学下册18.2平行四边形的判定获奖课件(22张PPT)
文档属性
| 名称 | 人教版八年级数学下册18.2平行四边形的判定获奖课件(22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 28.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-21 14:58:02 | ||
图片预览






文档简介
课件22张PPT。18.2平行四边形的判定
(1)衡阳县渣江镇
中心学校高小平 教学目标:
1.要求学生初步认识平行四边形的判定方法;
2.理解和掌握利用平行四边形的定义判定一个四边形是
平行四边形的判定方法;
3.理解和掌握平行四边形的判定定理1;
4.能正确运用上述方法解决实际问题 。 教学重点:
1.理解和掌握利用平行四边形的定义判定一个四边形是
平行四边形的判定方法;
2.理解和掌握平行四边形的判定定理1。
教学难点:
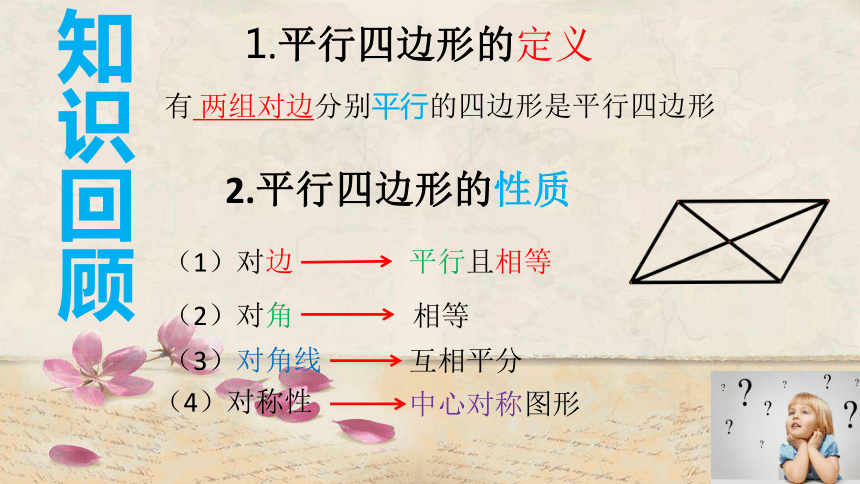
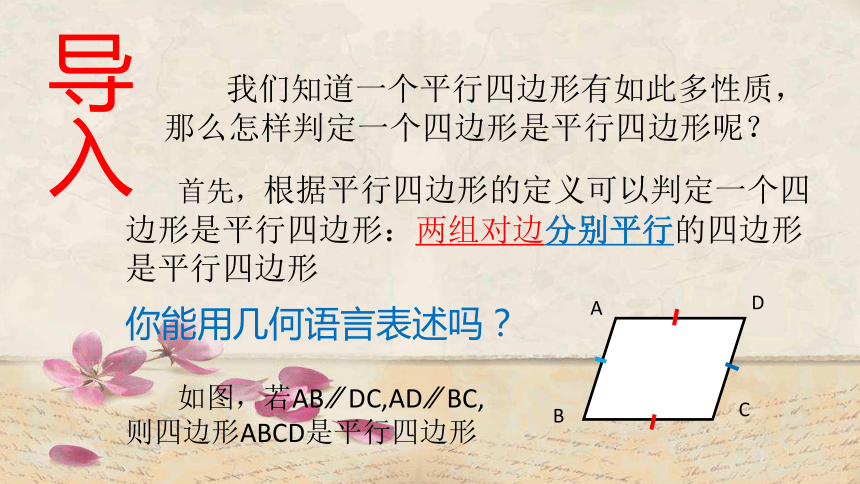
能正确运用平行四边形的定义和判定定理1解决实际问题。 1.平行四边形的定义知识回顾有 两组对边分别平行的四边形是平行四边形(1)对边 (2)对角 (3)对角线 中心对称图形平行且相等2.平行四边形的性质 相等互相平分(4)对称性 导入 我们知道一个平行四边形有如此多性质,那么怎样判定一个四边形是平行四边形呢? 首先,根据平行四边形的定义可以判定一个四边形是平行四边形:两组对边分别平行的四边形是平行四边形 如图,若AB ∕∕ DC,AD ∕∕ BC,
则四边形ABCD是平行四边形ABCD你能用几何语言表述吗?
两组对边分别平行的四边形
是平行四边形
由定义我们可以得到:判定方法一(边) 是否还有其它的判定方法呢?
导入 本节课我们就一起来探讨这个
问题 问题1 如图,若AB=CD,AD=BC,问AB ∕∕ CD吗?AD ∕∕ BC 吗?你能猜想四边形ABCD形状吗?请说明理由。如图 连结AC在?ABC和?CDA中 AB=CDBC=ADAC=CA ∴△ABC △CDA∴∠1=∠3 ∠2=∠4∴AB// CD AD//BC (已知)(已知)(公共边)(S . S . S)(全等三角形对应角相等)(内错角相等,两直线平行)∴四边形ABCD是平行四边形情景
探究(两组对边分别平行的四边形是平行四边形)1234≌ 两组对边分别相等
的四边形是平行四边形判定方法二(边)如图,四边形ABCD中,
若AB=DC,AD=BC,
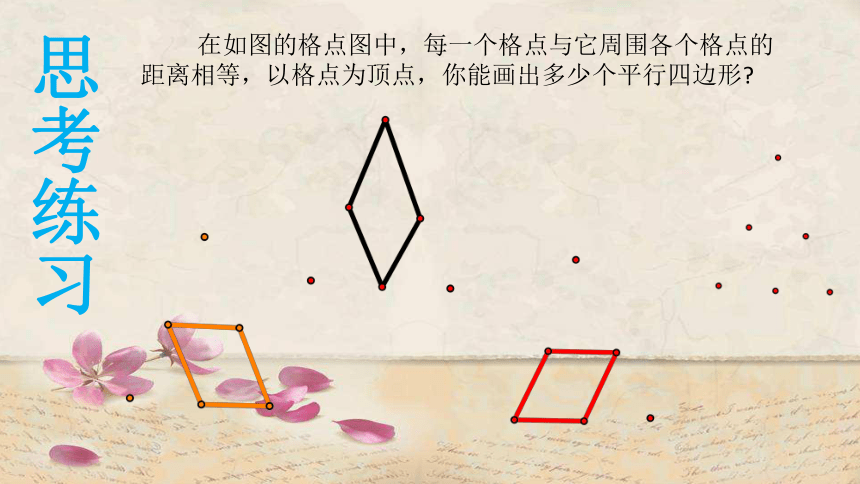
则四边形ABCD是平行四边形由此你可得到什么新的结论吗? 想一想 议一议 在如图的格点图中,每一个格点与它周围各个格点的
距离相等,以格点为顶点,你能画出多少个平行四边形?思考练习 如图,两个全等的三角形
拼成不同的平行四边形,最多
可以拼成( )
A.1个; B.2个; C.3个; D.4个。其根据是 。做一做 议一议C两组对边分别相等的四边形是平行四边形(1)(2)(3)参考答案例题分析 如图所示,在四边形ABCD中,AB=CD,BC=AD,E、F为对角线AC上的点,且AE=CF,
求证:(1)BE=DF (2)若连结BF和DE,四边形BFDE是平行四边形吗?若是,请说明理由。证明: ∵AB=CD, AD=BC∴四边形ABCD是平行四边形∴AB//CD∴∠BAE=∠DCF又∵AE=CF∴△ABE △DCF∴BE=DF(两组对边分别相等
的四边形是平行四边形)(1)(已知)(平行四边形的对边平行)(两直线平行,内错角相等。)(已知)(S.A.S)(全等三角形的对应边相等)≌情景探究(2) 与(1)同理可得 DE=BF又∵ BE=DF(1.中已证)∴四边形BFDE是平行四边形(两组对边分别相等的四边形是平行四边形)四边形BFDE 是平行四边形如图,连结BF和DE情景探究课堂练习1 如图,以A、B、O为
顶点构造平行四边形,
能构造几个平四边形?
写出第四个顶点的坐标。(4,2)(2,-2)(-2,2)参考答案 如图,在平行四边形ABCD中,E、F分别在边
AD、BC上,且AE=CF.
求证:(1)?ABE ?CDF;
(2)四边形BFDE是平行四边形.≌ABCDEF课堂 练习2 (1)∵四边形ABCD是平行四边形∴AD=BC, AB=CD, ∠ A=∠C又∵AE=CF。∴?ABE ?CDF(2)∵?ABE ?CDF∴BE=DF∵AD=BC, AE=CF∴ED=BF∴四边形BFDE是平行四边形≌≌(两组对边分别相等的四边形是
平行四边形)(S.A.S)(参考答案)知识小结平行四边形的判定方法方法一 两组对边分别平行的四边形
是平行四边形 方法二 两组对边分别相等的四边形
是平行四边形 作业 1.如图, 点A、B、C、D在同一条直线上,点E、F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC. 求 证 :四边形BECF是 平行四边形. 2.如图,将 ABCD 沿CE折叠,使
点D落在BC边上的F处,点E在AD上,请
猜想四边形ABFE的形状,并说明理由。(选做题)作业同学们,再见证明:在?ABE和?DCF中
AE=DF, ∠A=∠D, AB=DC
∴ ?ABE ?DCF
∴ BE=CF
又∵ AB=DC
∴ AC=DB≌ 在?AEC和?DFB中
AE=DF , ∠A=∠D, AC=DB
∴ ?AEC ?DFB
∴ EC=FB
∴ ≌四边形BECF是
平行四边形
(两组对边分别相等
的四边形是平行
四边形)
作业1 参考答案证明:由折叠的性质可知
EF=ED, ∠CFE=∠D∵四边形ABCD 是平行四边形,
∴ AD∥BC, ∠B=∠D∴AE∥BF , ∠B=∠CFE∴AB∥EF∴四边形ABFE是平行四边形(两组对边分别平行的四边形是平行四边形) 作业2 参考答案
(1)衡阳县渣江镇
中心学校高小平 教学目标:
1.要求学生初步认识平行四边形的判定方法;
2.理解和掌握利用平行四边形的定义判定一个四边形是
平行四边形的判定方法;
3.理解和掌握平行四边形的判定定理1;
4.能正确运用上述方法解决实际问题 。 教学重点:
1.理解和掌握利用平行四边形的定义判定一个四边形是
平行四边形的判定方法;
2.理解和掌握平行四边形的判定定理1。
教学难点:
能正确运用平行四边形的定义和判定定理1解决实际问题。 1.平行四边形的定义知识回顾有 两组对边分别平行的四边形是平行四边形(1)对边 (2)对角 (3)对角线 中心对称图形平行且相等2.平行四边形的性质 相等互相平分(4)对称性 导入 我们知道一个平行四边形有如此多性质,那么怎样判定一个四边形是平行四边形呢? 首先,根据平行四边形的定义可以判定一个四边形是平行四边形:两组对边分别平行的四边形是平行四边形 如图,若AB ∕∕ DC,AD ∕∕ BC,
则四边形ABCD是平行四边形ABCD你能用几何语言表述吗?
两组对边分别平行的四边形
是平行四边形
由定义我们可以得到:判定方法一(边) 是否还有其它的判定方法呢?
导入 本节课我们就一起来探讨这个
问题 问题1 如图,若AB=CD,AD=BC,问AB ∕∕ CD吗?AD ∕∕ BC 吗?你能猜想四边形ABCD形状吗?请说明理由。如图 连结AC在?ABC和?CDA中 AB=CDBC=ADAC=CA ∴△ABC △CDA∴∠1=∠3 ∠2=∠4∴AB// CD AD//BC (已知)(已知)(公共边)(S . S . S)(全等三角形对应角相等)(内错角相等,两直线平行)∴四边形ABCD是平行四边形情景
探究(两组对边分别平行的四边形是平行四边形)1234≌ 两组对边分别相等
的四边形是平行四边形判定方法二(边)如图,四边形ABCD中,
若AB=DC,AD=BC,
则四边形ABCD是平行四边形由此你可得到什么新的结论吗? 想一想 议一议 在如图的格点图中,每一个格点与它周围各个格点的
距离相等,以格点为顶点,你能画出多少个平行四边形?思考练习 如图,两个全等的三角形
拼成不同的平行四边形,最多
可以拼成( )
A.1个; B.2个; C.3个; D.4个。其根据是 。做一做 议一议C两组对边分别相等的四边形是平行四边形(1)(2)(3)参考答案例题分析 如图所示,在四边形ABCD中,AB=CD,BC=AD,E、F为对角线AC上的点,且AE=CF,
求证:(1)BE=DF (2)若连结BF和DE,四边形BFDE是平行四边形吗?若是,请说明理由。证明: ∵AB=CD, AD=BC∴四边形ABCD是平行四边形∴AB//CD∴∠BAE=∠DCF又∵AE=CF∴△ABE △DCF∴BE=DF(两组对边分别相等
的四边形是平行四边形)(1)(已知)(平行四边形的对边平行)(两直线平行,内错角相等。)(已知)(S.A.S)(全等三角形的对应边相等)≌情景探究(2) 与(1)同理可得 DE=BF又∵ BE=DF(1.中已证)∴四边形BFDE是平行四边形(两组对边分别相等的四边形是平行四边形)四边形BFDE 是平行四边形如图,连结BF和DE情景探究课堂练习1 如图,以A、B、O为
顶点构造平行四边形,
能构造几个平四边形?
写出第四个顶点的坐标。(4,2)(2,-2)(-2,2)参考答案 如图,在平行四边形ABCD中,E、F分别在边
AD、BC上,且AE=CF.
求证:(1)?ABE ?CDF;
(2)四边形BFDE是平行四边形.≌ABCDEF课堂 练习2 (1)∵四边形ABCD是平行四边形∴AD=BC, AB=CD, ∠ A=∠C又∵AE=CF。∴?ABE ?CDF(2)∵?ABE ?CDF∴BE=DF∵AD=BC, AE=CF∴ED=BF∴四边形BFDE是平行四边形≌≌(两组对边分别相等的四边形是
平行四边形)(S.A.S)(参考答案)知识小结平行四边形的判定方法方法一 两组对边分别平行的四边形
是平行四边形 方法二 两组对边分别相等的四边形
是平行四边形 作业 1.如图, 点A、B、C、D在同一条直线上,点E、F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC. 求 证 :四边形BECF是 平行四边形. 2.如图,将 ABCD 沿CE折叠,使
点D落在BC边上的F处,点E在AD上,请
猜想四边形ABFE的形状,并说明理由。(选做题)作业同学们,再见证明:在?ABE和?DCF中
AE=DF, ∠A=∠D, AB=DC
∴ ?ABE ?DCF
∴ BE=CF
又∵ AB=DC
∴ AC=DB≌ 在?AEC和?DFB中
AE=DF , ∠A=∠D, AC=DB
∴ ?AEC ?DFB
∴ EC=FB
∴ ≌四边形BECF是
平行四边形
(两组对边分别相等
的四边形是平行
四边形)
作业1 参考答案证明:由折叠的性质可知
EF=ED, ∠CFE=∠D∵四边形ABCD 是平行四边形,
∴ AD∥BC, ∠B=∠D∴AE∥BF , ∠B=∠CFE∴AB∥EF∴四边形ABFE是平行四边形(两组对边分别平行的四边形是平行四边形) 作业2 参考答案
