数学六年级上浙教版5 比的应用课件(37张)
文档属性
| 名称 | 数学六年级上浙教版5 比的应用课件(37张) |  | |
| 格式 | zip | ||
| 文件大小 | 15.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-22 17:48:54 | ||
图片预览









文档简介
课件37张PPT。六年级一班男生人数与女生人数的比是4 ∶5。提示:可以把男生人数看作( )份,女生人数有( )份。全班共有( )份。男生人数是女生人数的( ),女生人数是男生人数的( ),男生人数是全班总人数的( ),女生人数是全班总人数的( )。459复 习比 的 应 用在工农业生产和日常生活中,
常常需要把一个数量按照一定的比来分配,
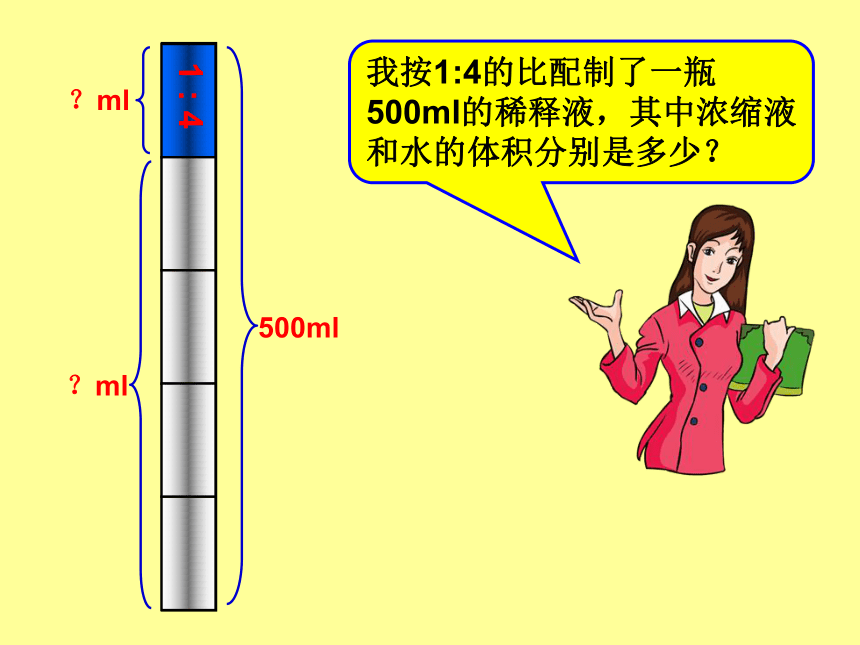
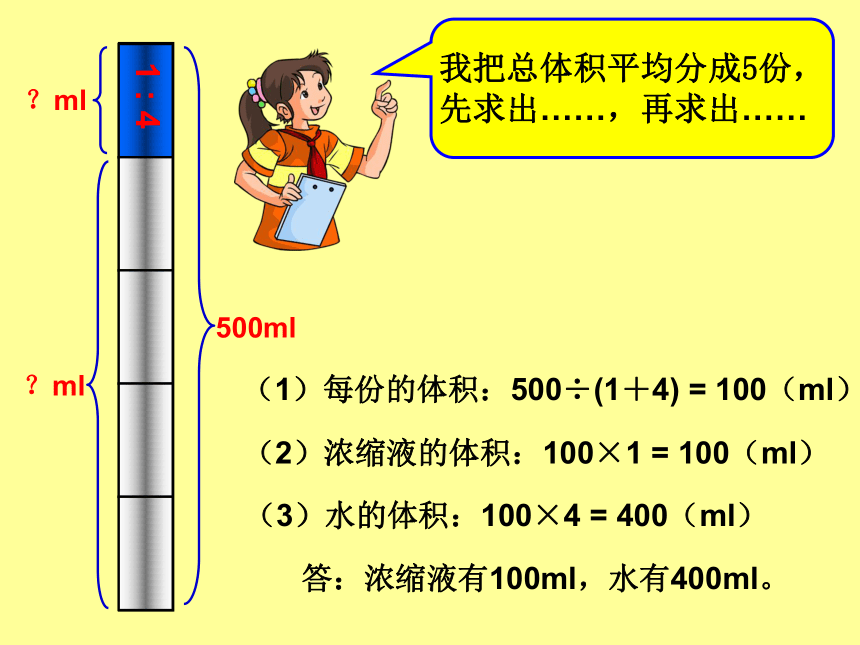
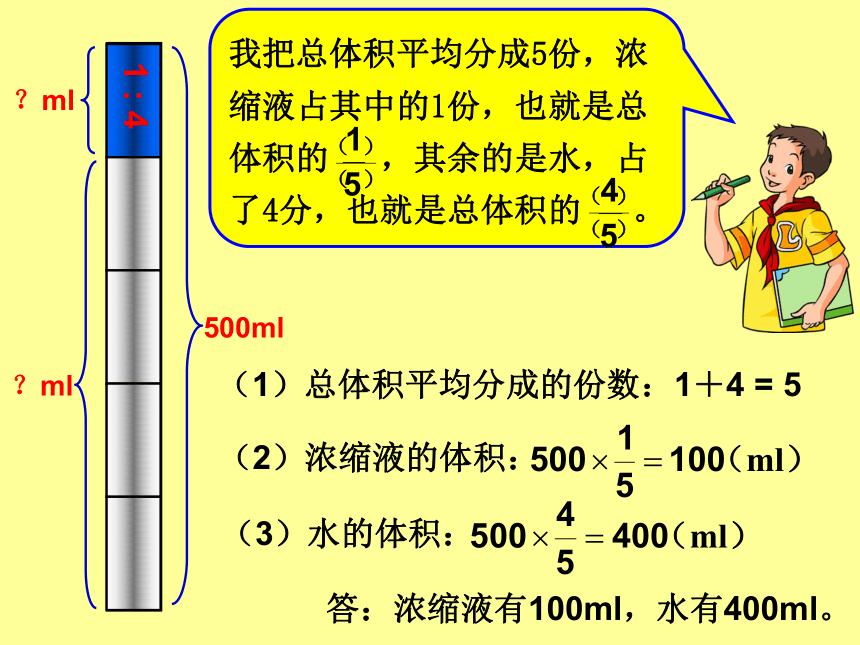
这种分配的方法通常叫做按比例分配。浓缩液稀释瓶稀释比例浓缩液和水的比是1 :42这是某种清洁剂浓缩液的稀释瓶,瓶子上标明的比表示浓缩液和水的体积之比。按照这些比,可以配制出不同浓度的稀释液。1 : 1浓缩液水1 : 21 : 31 : 41 : 5用完了,应该怎么来配制呢?我按1:4的比配制了一瓶500ml的稀释液,其中浓缩液和水的体积分别是多少?1 : 4500ml?ml?ml我把总体积平均分成5份,先求出……,再求出……(1)每份的体积:500÷(1+4) = 100(ml)(2)浓缩液的体积:100×1 = 100(ml)(3)水的体积:100×4 = 400(ml)答:浓缩液有100ml,水有400ml。1 : 4500ml?ml?ml(1)总体积平均分成的份数:1+4 = 5(2)浓缩液的体积:(3)水的体积:答:浓缩液有100ml,水有400ml。我把总体积平均分成5份,浓缩液占其中的1份,也就是总体积的 ,其余的是水,占了4分,也就是总体积的 。 1 : 4500ml?ml?ml已知总数和各部分数的比,求各部分数。按比例分配应用题的结构特征:方法与步骤:1、根据比先求出总份数。
2、求出各部分数占总数的几分之几。
3、运用分数乘法列式计算,求出各部分数。
4、答题并检验。小 结结构特征:
已知总数(各部分之和)和各部分数的比,求各部分数。
解题步骤:
1.根据比先求出总份数;
2.求出各部分数占总数的几分之几;
3.运用分数乘法列式计算,求出各部分
数,或平均每份是多少;
4.答题并检验。
练习:
1.学校把栽70棵树的任务,按照六年级三个班
的人数分配给各班。一班46人,二班44人,
三班50人。三个班各应栽树多少棵?巩固应用,拓展思路2.爸爸五月份的工资时3200元,这个月花去
的和剩下的钱数的比是5:3,花去的比剩下
的多多少元?3.水泥、沙子和石子的比是2:3:5.要搅拌20
吨这样的混凝土,需要水泥、沙子和石子
各多少吨?4.曹老师用60cm长的铁丝围成一个长方形的
教具,围成的长方形长和宽的比是3:2。求
这个长方形的长和宽分别是多少厘米?
5.用240cm长的铁丝围成一个长方体框架模型
围成的长方体的长、宽和高的比是3:2:1,
求这个长方体的长、宽和高分别是多少?已知一个量和比,求另外几个部分量。
例2 学校新进一批图书,按3:4:5的比分配给
四、五、六年级。五年级分得120本,四
年级和六年级各分得多少本?练习:
1.男工40人,男工与女工的比是4︰5,
女工有多少人?一共有多少人?
2.甲、乙两位工人的工作效率之比是3:2,
乙每小时生产36个零件,甲、乙两人合作
10分钟一共生产多少个零件?
解题步骤:
1.已知量÷对应的份数=每份的量。
2.每份量×相应份数=对应的量。已知两个量的比和它们的差,求总量。
例3
小华和爷爷的年龄比是1:6,已知小华的年龄比爷爷小50岁,小华和爷爷的年龄和是多少?解题步骤:
1.两个量的差÷两个量对应的份数差=每份数。
2.每份数×总份数=总数量。已知相差数和比
1.男工与女工的比是4:5,女比男多4人,
男、女各多少人?
2.一套西装,裤子的价格与上衣的比3:5是,
裤子比上衣便宜50元,上衣和裤子的价格
各是多少元?
3.两个城市相距360km,一辆客车和一辆货车
同时从这两个城市相对开出,3小时后相遇
已知客车和货车的速度比是5:7,客车和货
车每小时各行驶多少千米?连比
1.若甲与乙的比是4:3,乙与丙的比是5:6,
甲:乙:丙=( ):( ):( )
2.小芳与小玲步行的速度比是2:3,小玲与
小红步行的速度比是4:5,三人1分钟所行
的路程和是175米。三个小伙伴每分钟各
行了多少米?
3.甲数的 等于乙数的 ,乙数的
等于丙数的 。甲乙丙三数的最简比是
多少?例4
聪聪和笑笑共收集邮票171枚。已知聪聪收集
票数的 和笑笑收集票数的 相等。求
聪聪和笑笑分别收集邮票多少枚?
总结:
已知甲、乙两个量的和,且甲× =乙×
(a,b均不为0),通过示意图可以明确甲、乙
两个量的比就是a:b。练习:
1.甲乙两个班的共有81人,其中甲班人数的
和乙班人数的 相等。甲、乙两班各
有多少人?
例5
一条路全长360km,分成上坡、平路、下坡三段,三段路程之比是1:2:3,小明走完三段路程所用的时间之比是4:5:6,已知他上坡的速度是5km/h,小明走完全程用了多长时间?练习
1.一条路全长60km,分成上坡、平路、下坡
三段,三段路程之比是1:2:3,小明走完三
段路程所用的时间之比是4:5:6,已知他
上坡的速度是3km/h,小明走完全程用了多
长时间?2.甲、乙、丙三人合作加工一批零件,加工
一个零件甲需要6分钟,乙需要5分钟,丙
需要4.5分钟,三人完成加工任务后共得工
钱1590元。按照加工零件的数量分工钱,
甲、乙、丙三人各分得工钱多少元?例1
春节快来啦!水果批发商张老板购进了1420箱苹果、香蕉和梨,苹果和香蕉的箱数比是4:3,梨比香蕉少180箱。苹果、香蕉和梨三种水果各购进了多少箱?
练习:
书上P83-奥赛训练
例2
甲、乙两个服装厂12月份生产服装的数量比是6:7,两个厂服装的单价比是11:10,并且这两个厂这个月的总产值是8160万元,两个服装厂这个月的产值分别是多少万元?
练习:
书上P85-奥赛训练例3
甲数的 等于乙数的 ,乙数的 等于丙数
的 ,那么,甲、乙、丙三个数的最简比是
多少?
练习:
书上P86-举一反三例4
强强、笑笑和甜甜三人共有147元,强强用了
自己钱数的 ,笑笑用了自己钱数的 ,
甜甜用了自己钱数的 ,各买了一支相同的钢笔,那么三个好朋友原来各有多少元?
练习:
书上P87-奥赛训练
例5
有甲、乙两个粮食仓库,原来甲粮库存粮的
吨数是乙粮库的 ,如果从乙粮库调6吨粮
食到甲粮库,那么甲粮库存粮的吨数与乙粮
库存粮的吨数比就是4:5,原来甲、乙粮库各
存粮多少吨?
练习:书上P88举一反三例6
有甲、乙两个粮食库,原来甲粮库存粮的吨
数与乙粮库的比是4:5,如果从甲粮库调
到乙粮库,乙粮库存粮的吨数比甲粮库存粮多46吨。原来甲、乙粮库各存粮多少吨?
练习:书上P90-奥赛训练假设已知量两个容器中装着重量相同的盐水,第一个容器中盐和水的比是1:9,第二个容器中盐和水的比是1:3,把这两个容器中的盐水倒入一个更大的容器内,混合盐水中的盐和水的比是多少?
常常需要把一个数量按照一定的比来分配,
这种分配的方法通常叫做按比例分配。浓缩液稀释瓶稀释比例浓缩液和水的比是1 :42这是某种清洁剂浓缩液的稀释瓶,瓶子上标明的比表示浓缩液和水的体积之比。按照这些比,可以配制出不同浓度的稀释液。1 : 1浓缩液水1 : 21 : 31 : 41 : 5用完了,应该怎么来配制呢?我按1:4的比配制了一瓶500ml的稀释液,其中浓缩液和水的体积分别是多少?1 : 4500ml?ml?ml我把总体积平均分成5份,先求出……,再求出……(1)每份的体积:500÷(1+4) = 100(ml)(2)浓缩液的体积:100×1 = 100(ml)(3)水的体积:100×4 = 400(ml)答:浓缩液有100ml,水有400ml。1 : 4500ml?ml?ml(1)总体积平均分成的份数:1+4 = 5(2)浓缩液的体积:(3)水的体积:答:浓缩液有100ml,水有400ml。我把总体积平均分成5份,浓缩液占其中的1份,也就是总体积的 ,其余的是水,占了4分,也就是总体积的 。 1 : 4500ml?ml?ml已知总数和各部分数的比,求各部分数。按比例分配应用题的结构特征:方法与步骤:1、根据比先求出总份数。
2、求出各部分数占总数的几分之几。
3、运用分数乘法列式计算,求出各部分数。
4、答题并检验。小 结结构特征:
已知总数(各部分之和)和各部分数的比,求各部分数。
解题步骤:
1.根据比先求出总份数;
2.求出各部分数占总数的几分之几;
3.运用分数乘法列式计算,求出各部分
数,或平均每份是多少;
4.答题并检验。
练习:
1.学校把栽70棵树的任务,按照六年级三个班
的人数分配给各班。一班46人,二班44人,
三班50人。三个班各应栽树多少棵?巩固应用,拓展思路2.爸爸五月份的工资时3200元,这个月花去
的和剩下的钱数的比是5:3,花去的比剩下
的多多少元?3.水泥、沙子和石子的比是2:3:5.要搅拌20
吨这样的混凝土,需要水泥、沙子和石子
各多少吨?4.曹老师用60cm长的铁丝围成一个长方形的
教具,围成的长方形长和宽的比是3:2。求
这个长方形的长和宽分别是多少厘米?
5.用240cm长的铁丝围成一个长方体框架模型
围成的长方体的长、宽和高的比是3:2:1,
求这个长方体的长、宽和高分别是多少?已知一个量和比,求另外几个部分量。
例2 学校新进一批图书,按3:4:5的比分配给
四、五、六年级。五年级分得120本,四
年级和六年级各分得多少本?练习:
1.男工40人,男工与女工的比是4︰5,
女工有多少人?一共有多少人?
2.甲、乙两位工人的工作效率之比是3:2,
乙每小时生产36个零件,甲、乙两人合作
10分钟一共生产多少个零件?
解题步骤:
1.已知量÷对应的份数=每份的量。
2.每份量×相应份数=对应的量。已知两个量的比和它们的差,求总量。
例3
小华和爷爷的年龄比是1:6,已知小华的年龄比爷爷小50岁,小华和爷爷的年龄和是多少?解题步骤:
1.两个量的差÷两个量对应的份数差=每份数。
2.每份数×总份数=总数量。已知相差数和比
1.男工与女工的比是4:5,女比男多4人,
男、女各多少人?
2.一套西装,裤子的价格与上衣的比3:5是,
裤子比上衣便宜50元,上衣和裤子的价格
各是多少元?
3.两个城市相距360km,一辆客车和一辆货车
同时从这两个城市相对开出,3小时后相遇
已知客车和货车的速度比是5:7,客车和货
车每小时各行驶多少千米?连比
1.若甲与乙的比是4:3,乙与丙的比是5:6,
甲:乙:丙=( ):( ):( )
2.小芳与小玲步行的速度比是2:3,小玲与
小红步行的速度比是4:5,三人1分钟所行
的路程和是175米。三个小伙伴每分钟各
行了多少米?
3.甲数的 等于乙数的 ,乙数的
等于丙数的 。甲乙丙三数的最简比是
多少?例4
聪聪和笑笑共收集邮票171枚。已知聪聪收集
票数的 和笑笑收集票数的 相等。求
聪聪和笑笑分别收集邮票多少枚?
总结:
已知甲、乙两个量的和,且甲× =乙×
(a,b均不为0),通过示意图可以明确甲、乙
两个量的比就是a:b。练习:
1.甲乙两个班的共有81人,其中甲班人数的
和乙班人数的 相等。甲、乙两班各
有多少人?
例5
一条路全长360km,分成上坡、平路、下坡三段,三段路程之比是1:2:3,小明走完三段路程所用的时间之比是4:5:6,已知他上坡的速度是5km/h,小明走完全程用了多长时间?练习
1.一条路全长60km,分成上坡、平路、下坡
三段,三段路程之比是1:2:3,小明走完三
段路程所用的时间之比是4:5:6,已知他
上坡的速度是3km/h,小明走完全程用了多
长时间?2.甲、乙、丙三人合作加工一批零件,加工
一个零件甲需要6分钟,乙需要5分钟,丙
需要4.5分钟,三人完成加工任务后共得工
钱1590元。按照加工零件的数量分工钱,
甲、乙、丙三人各分得工钱多少元?例1
春节快来啦!水果批发商张老板购进了1420箱苹果、香蕉和梨,苹果和香蕉的箱数比是4:3,梨比香蕉少180箱。苹果、香蕉和梨三种水果各购进了多少箱?
练习:
书上P83-奥赛训练
例2
甲、乙两个服装厂12月份生产服装的数量比是6:7,两个厂服装的单价比是11:10,并且这两个厂这个月的总产值是8160万元,两个服装厂这个月的产值分别是多少万元?
练习:
书上P85-奥赛训练例3
甲数的 等于乙数的 ,乙数的 等于丙数
的 ,那么,甲、乙、丙三个数的最简比是
多少?
练习:
书上P86-举一反三例4
强强、笑笑和甜甜三人共有147元,强强用了
自己钱数的 ,笑笑用了自己钱数的 ,
甜甜用了自己钱数的 ,各买了一支相同的钢笔,那么三个好朋友原来各有多少元?
练习:
书上P87-奥赛训练
例5
有甲、乙两个粮食仓库,原来甲粮库存粮的
吨数是乙粮库的 ,如果从乙粮库调6吨粮
食到甲粮库,那么甲粮库存粮的吨数与乙粮
库存粮的吨数比就是4:5,原来甲、乙粮库各
存粮多少吨?
练习:书上P88举一反三例6
有甲、乙两个粮食库,原来甲粮库存粮的吨
数与乙粮库的比是4:5,如果从甲粮库调
到乙粮库,乙粮库存粮的吨数比甲粮库存粮多46吨。原来甲、乙粮库各存粮多少吨?
练习:书上P90-奥赛训练假设已知量两个容器中装着重量相同的盐水,第一个容器中盐和水的比是1:9,第二个容器中盐和水的比是1:3,把这两个容器中的盐水倒入一个更大的容器内,混合盐水中的盐和水的比是多少?
同课章节目录
- 一 比和百分比
- 1、生活中的比
- 2、比与除法
- 3、比的基本性质
- 4、图形的放大和缩小
- 5、比的应用
- 6、认识百分比
- 7、小数或分数化成百分比
- 8、百分数化成小数或分数
- 9、百分数的应用(一)
- 10、百分数的应用(二)
- 二 分数和百分数应用问题
- 11、应用问题(一)
- 12、应用问题(二)
- 13、折扣和利润
- 14、利息和纳税
- 三 圆的周长与面积
- 15、圆的周长
- 16、圆的面积
- 17、圆与正方形
- 18、扇形
- 四 统计与可能性
- 19、扇形统计图
- 20、可能性大小
- 21、身高和体重
- 五 用水中的数学问题
- 22、地球水资源
- 23、中国水资源
- 24、分析用水量
- 25、节约用水
- 26、防止水污染
- 六 总复习
- 总复习
