人教版八年级数学下册18.1.2平行四边形的判定——三角形中位线课件(第3课时,共23张PPT)
文档属性
| 名称 | 人教版八年级数学下册18.1.2平行四边形的判定——三角形中位线课件(第3课时,共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 943.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-23 10:10:53 | ||
图片预览


文档简介
课件23张PPT。19.1.2平行四边形的判定(3)
——三角形中位线定理1.理解三角形中位线的概念,掌握三角形的中位线定理.(重点)
2.能利用三角形的中位线定理解决有关证明和计算问题.(重点)我们探索平行四边形时,常常转化为三角形,利用三角形的全等性质进行研究,今天我们一起来利用平行四边形来探索三角形的某些问题吧.思考 如图,有一块三角形蛋糕,准备平分给四个小朋友,要求四人所分的形状大小相同,该怎样分呢?问题引入按要求画图:
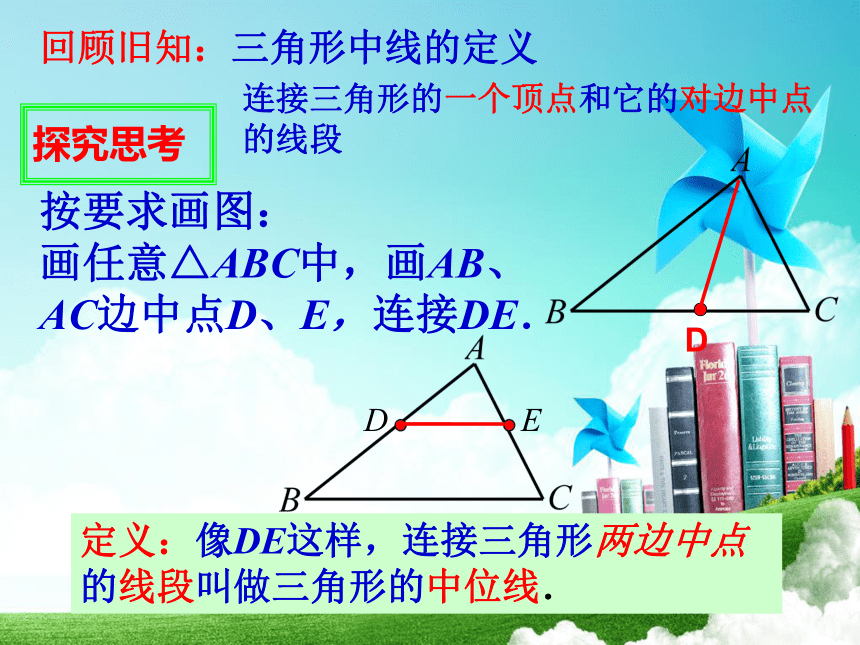
画任意△ABC中,画AB、
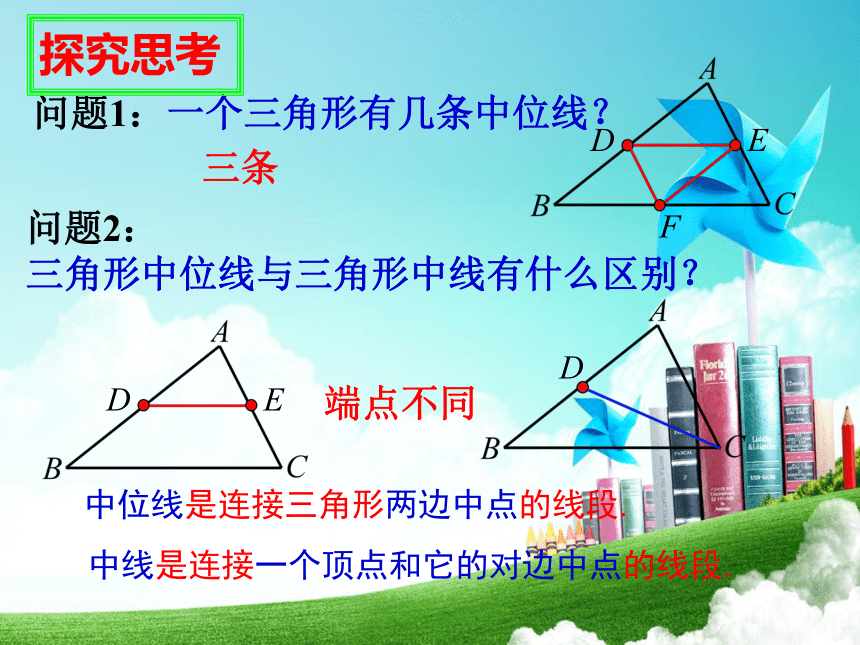
AC边中点D、E,连接DE.探究思考定义:像DE这样,连接三角形两边中点的线段叫做三角形的中位线.回顾旧知:三角形中线的定义连接三角形的一个顶点和它的对边中点的线段问题1:一个三角形有几条中位线?三条问题2:
三角形中位线与三角形中线有什么区别?端点不同探究思考FD中位线是连接三角形两边中点的线段. 中线是连接一个顶点和它的对边中点的线段.问题3:
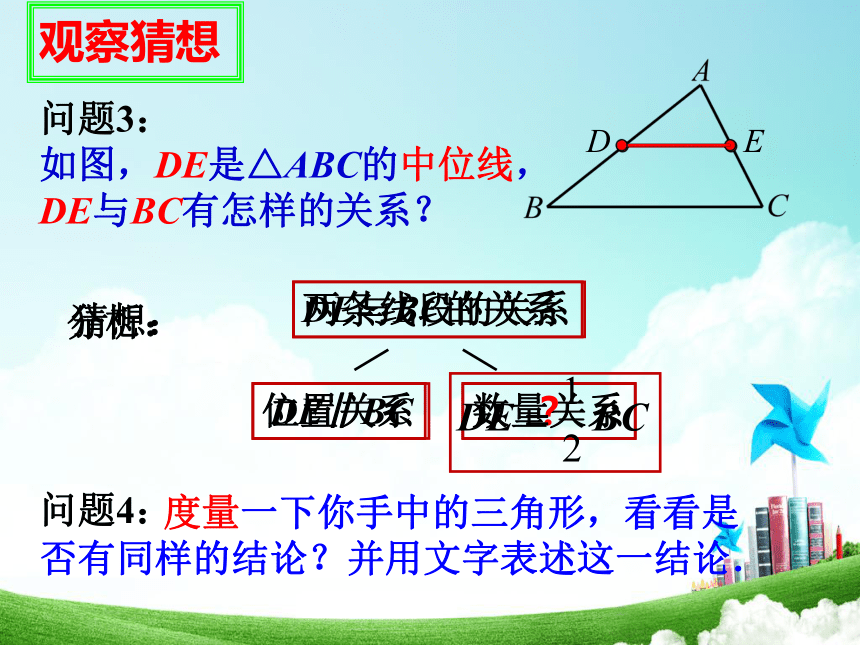
如图,DE是△ABC的中位线,
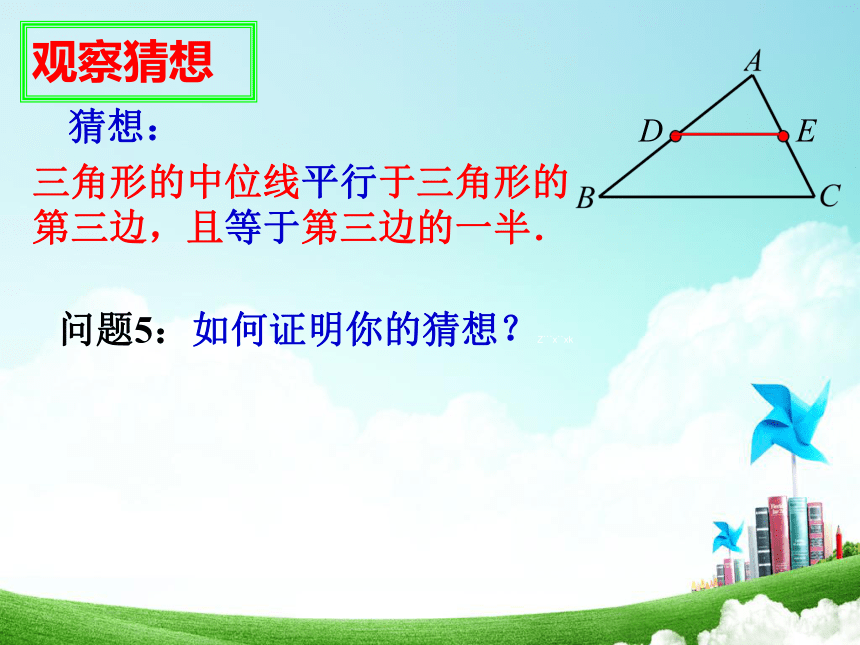
DE与BC有怎样的关系?两条线段的关系位置关系数量关系分析:DE与BC的关系猜想:DE∥BC?问题4:观察猜想 度量一下你手中的三角形,看看是否有同样的结论?并用文字表述这一结论.观察猜想三角形的中位线平行于三角形的
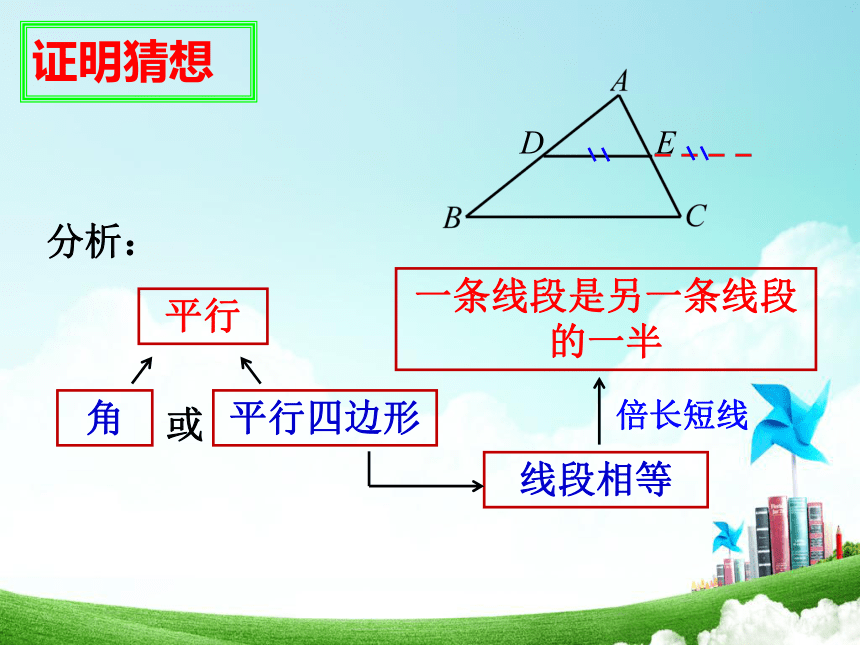
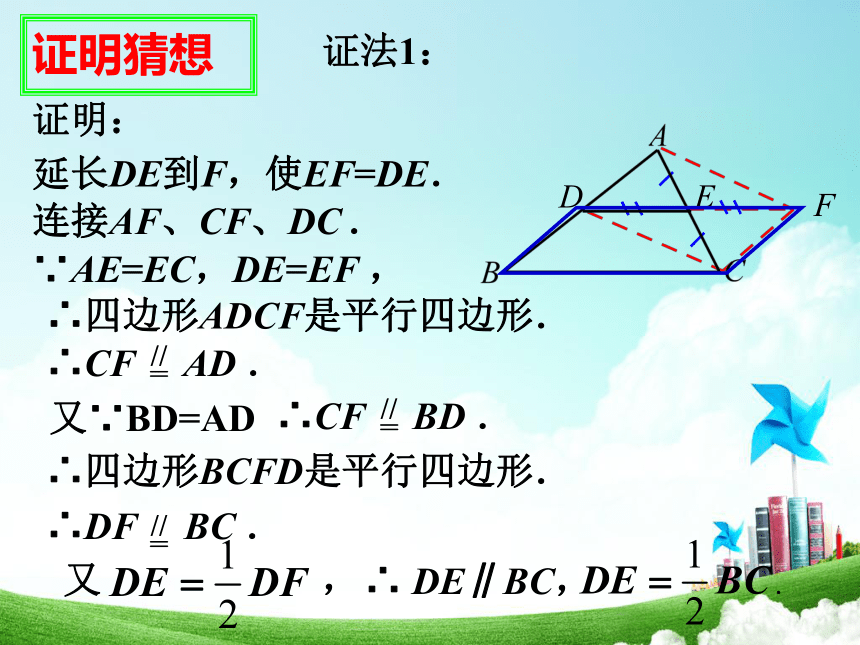
第三边,且等于第三边的一半. 问题5:如何证明你的猜想?Z```x``xk猜想:平行角平行四边形或线段相等一条线段是另一条线段的一半倍长短线分析:证明猜想证明猜想证明:延长DE到F,使EF=DE.连接AF、CF、DC .∵AE=EC,DE=EF ,∴四边形ADCF是平行四边形.∴四边形BCFD是平行四边形.证法1:∴ DE∥BC, .F又∵BD=AD证明猜想证明:证法2:∴ DE∥BC, .延长DE到F,使EF=DE.∴四边形BCFD是平行四边形.∴△ADE≌△CFE.∴∠ADE=∠F,AD=CF连接FC.∵EF=DE,∠AED=∠CEF,AE=CE,F又∵AD=BD三角形的中位线平行于三角形的
第三边且等于第三边的一半.三角形中位线定理:符号语言:归纳总结 三角形的中位线具有证两直线平行(平移角度)和证线段的倍分关系的作用。
“遇两中点想中位线” 如图,D、E、F分别是△ABC的三边的中点,那么,DE、DF、EF都是△ABC的中位线。F由此可知:……由三角形中位线定理可知:F重要发现:①中位线DE、EF、DF把△ABC
分成四个全等的三角形;有三
组共边的平行四边形,它们是
四边形ADFE和BDEF,四边形
BFED和CFDE,四边形ADFE
和DFCE.②顶点是中点的三角形,我们称之为中点三角形;中点三角形的周长是原三角形的周长的一半.面积等于原三角形面积的四分之一.由此你知道怎样分蛋糕了吗应用新知 1. 如图,△ABC中,D、E分别是AB、AC中点.(1) 若DE=5,则BC= .(2) 若∠B=65°,则∠ADE= °.(3) 若DE+BC=12,则BC= .1065x2xx+2x=12x=48 例:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA中点.
求证:四边形EFGH是平行四边形.四边形问题连接对角线三角形问题(三角形中位线定理)学以致用转化思想应用新知 2. 如图,A、B两点被池塘隔开,在AB外选一点
C,连接AC和BC,怎样量出A、B两点间的距离?
根据是什么? 分别画出AC、BC中点M、N,
量出M、N两点间距离,则AB=2MN.NM根据是三角形中位线定理.例2:如图,△ABC中,D是AB上一点,且
AD=AC , AE⊥CD于E,F是CB的中点。
求证:BD=2EF证明:又变式:如图,△ABC中,M是BC的中点,AD是∠ B AC的平分线 , BD⊥AD于D,AB=12, AC=18. 求DM的长.1218N△ ADB ≌ △ ADN63 3. 如图,在四边形ABCD中,AB=CD,M、N、P分别是AD、BC、BD的中点,∠ABD=20°,∠BDC=70°,求∠PMN的度数应用新知应用新知小结 1.本节课你学习了哪些知识?三角形的中位线定义、定理(1)三角形的中位线定理不仅给出了中位线与第三边的关系,而且给出了他们的数量关系,在三角形中给出一边的中点时,要转化为中位线.(2)线段的倍分要转化为相等问题来解决.(3)三角形的中位线定理的发现过程所用到的数学方法(包括画图、实验、猜想、分析、归纳等.) 2.你有什么收获?1.如图,D、E分别是△ABC的边AB、AC的中
点,点O是△ABC内部任意一点,连接OB、
OC,点G、F分别是OB、OC的中点,顺次
连接点D、G、F、E.
求证:四边形DGFE是平行四边形.GFEDO课后习题2.如图,在四边形ABCD中,对角线AC,BD相交于点O,且 ,E,F分别是AB,CD的中点,EF分别交BD,AC于点G , H。
求证:HGOFEAC=BDOG=OH课后习题
——三角形中位线定理1.理解三角形中位线的概念,掌握三角形的中位线定理.(重点)
2.能利用三角形的中位线定理解决有关证明和计算问题.(重点)我们探索平行四边形时,常常转化为三角形,利用三角形的全等性质进行研究,今天我们一起来利用平行四边形来探索三角形的某些问题吧.思考 如图,有一块三角形蛋糕,准备平分给四个小朋友,要求四人所分的形状大小相同,该怎样分呢?问题引入按要求画图:
画任意△ABC中,画AB、
AC边中点D、E,连接DE.探究思考定义:像DE这样,连接三角形两边中点的线段叫做三角形的中位线.回顾旧知:三角形中线的定义连接三角形的一个顶点和它的对边中点的线段问题1:一个三角形有几条中位线?三条问题2:
三角形中位线与三角形中线有什么区别?端点不同探究思考FD中位线是连接三角形两边中点的线段. 中线是连接一个顶点和它的对边中点的线段.问题3:
如图,DE是△ABC的中位线,
DE与BC有怎样的关系?两条线段的关系位置关系数量关系分析:DE与BC的关系猜想:DE∥BC?问题4:观察猜想 度量一下你手中的三角形,看看是否有同样的结论?并用文字表述这一结论.观察猜想三角形的中位线平行于三角形的
第三边,且等于第三边的一半. 问题5:如何证明你的猜想?Z```x``xk猜想:平行角平行四边形或线段相等一条线段是另一条线段的一半倍长短线分析:证明猜想证明猜想证明:延长DE到F,使EF=DE.连接AF、CF、DC .∵AE=EC,DE=EF ,∴四边形ADCF是平行四边形.∴四边形BCFD是平行四边形.证法1:∴ DE∥BC, .F又∵BD=AD证明猜想证明:证法2:∴ DE∥BC, .延长DE到F,使EF=DE.∴四边形BCFD是平行四边形.∴△ADE≌△CFE.∴∠ADE=∠F,AD=CF连接FC.∵EF=DE,∠AED=∠CEF,AE=CE,F又∵AD=BD三角形的中位线平行于三角形的
第三边且等于第三边的一半.三角形中位线定理:符号语言:归纳总结 三角形的中位线具有证两直线平行(平移角度)和证线段的倍分关系的作用。
“遇两中点想中位线” 如图,D、E、F分别是△ABC的三边的中点,那么,DE、DF、EF都是△ABC的中位线。F由此可知:……由三角形中位线定理可知:F重要发现:①中位线DE、EF、DF把△ABC
分成四个全等的三角形;有三
组共边的平行四边形,它们是
四边形ADFE和BDEF,四边形
BFED和CFDE,四边形ADFE
和DFCE.②顶点是中点的三角形,我们称之为中点三角形;中点三角形的周长是原三角形的周长的一半.面积等于原三角形面积的四分之一.由此你知道怎样分蛋糕了吗应用新知 1. 如图,△ABC中,D、E分别是AB、AC中点.(1) 若DE=5,则BC= .(2) 若∠B=65°,则∠ADE= °.(3) 若DE+BC=12,则BC= .1065x2xx+2x=12x=48 例:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA中点.
求证:四边形EFGH是平行四边形.四边形问题连接对角线三角形问题(三角形中位线定理)学以致用转化思想应用新知 2. 如图,A、B两点被池塘隔开,在AB外选一点
C,连接AC和BC,怎样量出A、B两点间的距离?
根据是什么? 分别画出AC、BC中点M、N,
量出M、N两点间距离,则AB=2MN.NM根据是三角形中位线定理.例2:如图,△ABC中,D是AB上一点,且
AD=AC , AE⊥CD于E,F是CB的中点。
求证:BD=2EF证明:又变式:如图,△ABC中,M是BC的中点,AD是∠ B AC的平分线 , BD⊥AD于D,AB=12, AC=18. 求DM的长.1218N△ ADB ≌ △ ADN63 3. 如图,在四边形ABCD中,AB=CD,M、N、P分别是AD、BC、BD的中点,∠ABD=20°,∠BDC=70°,求∠PMN的度数应用新知应用新知小结 1.本节课你学习了哪些知识?三角形的中位线定义、定理(1)三角形的中位线定理不仅给出了中位线与第三边的关系,而且给出了他们的数量关系,在三角形中给出一边的中点时,要转化为中位线.(2)线段的倍分要转化为相等问题来解决.(3)三角形的中位线定理的发现过程所用到的数学方法(包括画图、实验、猜想、分析、归纳等.) 2.你有什么收获?1.如图,D、E分别是△ABC的边AB、AC的中
点,点O是△ABC内部任意一点,连接OB、
OC,点G、F分别是OB、OC的中点,顺次
连接点D、G、F、E.
求证:四边形DGFE是平行四边形.GFEDO课后习题2.如图,在四边形ABCD中,对角线AC,BD相交于点O,且 ,E,F分别是AB,CD的中点,EF分别交BD,AC于点G , H。
求证:HGOFEAC=BDOG=OH课后习题
