8.2消元--解二元一次方程组(加减法)课件(共44张PPT)
文档属性
| 名称 | 8.2消元--解二元一次方程组(加减法)课件(共44张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-23 00:00:00 | ||
图片预览










文档简介
课件44张PPT。加减消元二元一次方程组解法2、用代入法解方程的关键是什么?1、根据等式性质填空:思考:若a=b,c=d,那么a+c=b+d吗?3、解二元一次方程组的基本思路是什么?b±cbc(等式性质1)(等式性质2)<2>若a=b,那么ac= .<1>若a=b,那么a±c= .消元:复习:主要步骤: 基本思路:4、写解 3、求解2、代入把变形后的方程代入到另一个方程中,消去一个元分别求出两个未知数的值写出方程组的解1、变形用含有一个未知数的代数式表示另一个未知数,写成y=ax+b或x=ay+b消元: 二元1、解二元一次方程组的基本思路是什么?2、用代入法解方程的步骤是什么?一元问题用代入法怎样解下面的二元一次方程组呢?问题怎样解下面的二元一次方程组呢?代入消元法y还别的方法吗? 认真观察此方程组中各个未知数的系数有什么特点,并分组讨论看还有没有其它的解法.
并尝试一下能否求出它的解问题 观察方程组中的两个方程,未知数y的系数相等。把两个方程两边分别相减,就可以消去未知数y,得到一个一元一次方程。 即?-?,消去未知数y,得 x=6
把x=6代入? ,得 y=4
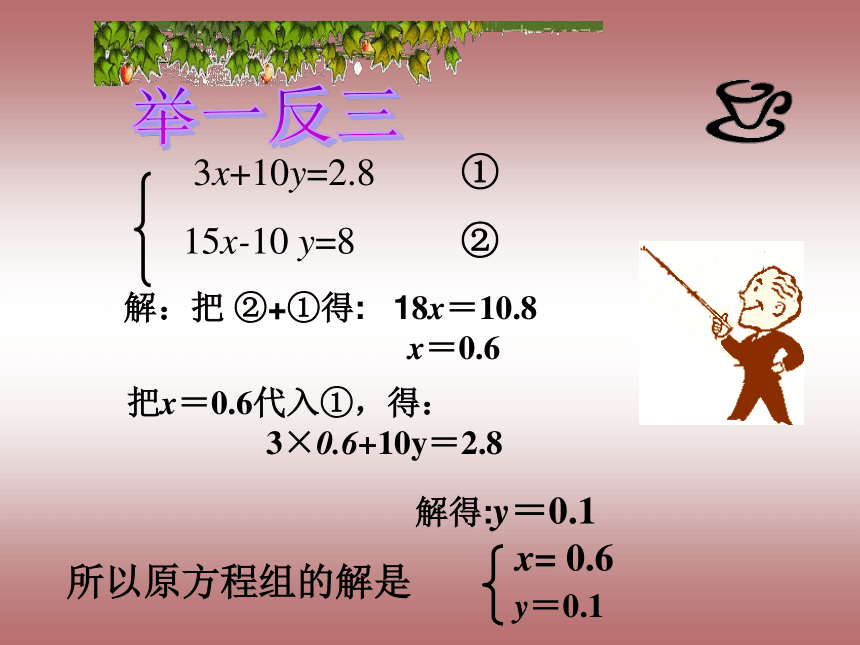
3x+10y=2.8 ①
15x-10 y=8 ② 观察方程组中的两个方程,未知数y的系数相反。把两个方程两边分别相加,就可以消去未知数y,同样得到一个一元一次方程。分析:举一反三解方程组解:把 ②+①得: 18x=10.8
x=0.6把x=0.6代入①,得:
3×0.6+10y=2.8解得:y=0.1举一反三3x+10y=2.8 ①
15x-10 y=8 ②
分析: 3x+5y +2x - 5y=10 ①左边 + ② 左边 = ① 右边 + ②右边5x =10
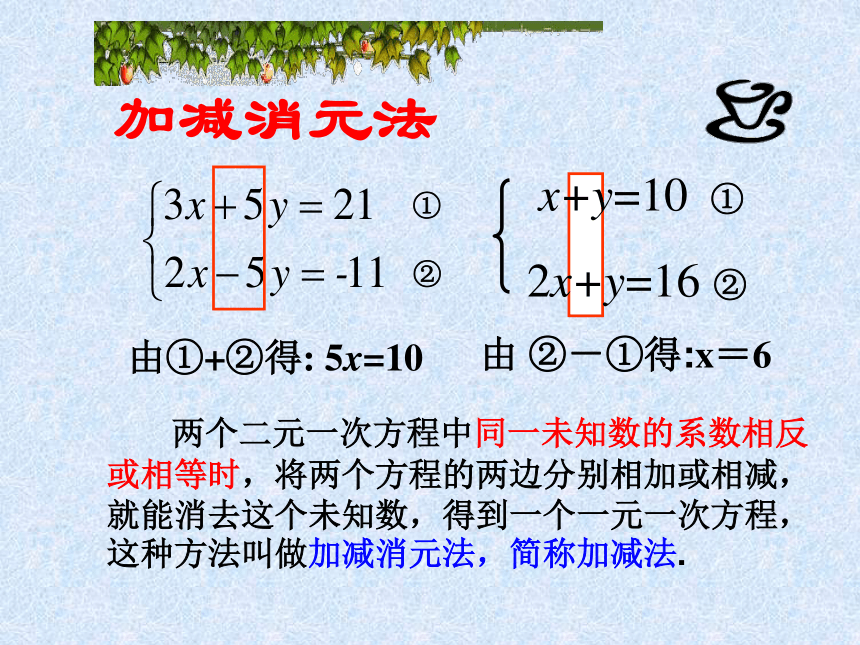
x=2(3x + 5y)+(2x - 5y)=21 + (-11)等式性质解:由①+②得: 5x=10 把x=2代入①,得: y=3 x=2新思路 新体验加减消元法 两个二元一次方程中同一未知数的系数相反或相等时,将两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法.由①+②得: 5x=10 x+y=10 ①
2x+y=16 ②由 ②-①得:x=6分别相加y1.已知方程组x+3y=172x-3y=6两个方程就可以消去未知数分别相减2.已知方程组25x-7y=1625x+6y=10两个方程就可以消去未知数x一.填空题:只要两边只要两边练习二.选择题B2.方程组3x+2y=133x-2y=5消去y后所得的方程是( )BA.6x=8B.6x=18C.6x=5D.x=18 三.指出下列方程组求解过程中有错误步骤,并给予订正:7x-4y=4
5x-4y=-4
解:①-②,得
2x=4-4,
x=0
①①②②3x-4y=14
5x+4y=2
解 ①-②,得
-2x=12
x =-6解: ①-②,得
2x=4+4,
x=4解: ①+②,得
8x=16
x =2
看看你掌握了吗? 上面这些方程组的特点是什么?
解这类方程组基本思路是什么?
主要步骤有哪些?想一想,议一议:主要步骤:
特点:基本思路:写解求解加减二元一元加减消元:消去一个元分别求出两个未知数的值写出原方程组的解同一个未知数的系数相同或互为相反数解方程本例题可以用加减
消元法来做吗?
问题1.这两个方程直接相加减能消去未知数吗?为什么? 问题2.那么怎样使方程组中某一未知数系数的绝对值相等呢?
分 析: 对于当方程组中两方程不具备上述特点时,则可用等式性质来改变方程组中方程的形式,即得到与原方程组同解的且某未知数系数的绝对值相等的新的方程组,从而为加减消元法解方程组创造条件.应用新知3x+4y=165x-6y=33二
元
一
次
方
程
组15x+20y=8015x-18y=9938y=-19x=6解得y代入3x+4y=16②×3使未知数x系数相等①×5两式相减消
x解得x解方程组:解法一:① ×3 得 19x = 114 把x = 6代入①得所以这个方程组的解为 即 x = 618 + 4y = 169x+ 12y = 48 ② ×2 得10x - 12y = 66 ③ + ④ 得即 y = ④ ③①②解方程组:解法二:① ×5 得 38y = -19 即 x = 615x+ 20y = 80 ② ×3 得15x - 18y = 99 ③ - ④ 得④ ③①②3x-2 = 16所以这个方程组的解为解:由①×6,得2x+3y=4 ③由②×4,得 2x - y=8 ④由③-④得: y= -1所以原方程组
的解是把y= -1代入② ,
解得:②①
补充练习:用加减消元法解方程组:练习:用加减法解方程组:(1)(2)加减法归纳: 用加减法解同一个未知数的系数绝对值不相等的二元一次方程组时,把一个(或两个)方程的两边乘以适当的数,使两个方程中某一未知数的系数绝对值相等,从而化为第一类型方程组求解.
例4 2台大收割机和5台小收割机工作2小时收割小麦3.6公顷;3台大收割机和2台小收割机工作5小时收割小麦8公顷。1台大收割机和1台小收割机工作1小时各收割小麦多少公顷?解: 大收割机小收割机效率时间工作量xy22台数5(2x+ 5y)2= 3.6创设情境 2台大收割机和5台小收割机工作2小时收割小麦3.6公顷;3台大收割机和2台小收割机工作5小时收割小麦8公顷。1台大收割机和1台小收割机工作1小时各收割小麦多少公顷?解: 大收割机小收割机效率时间工作量xy35台数2(3x+ 2y)5= 8 2台大收割机和5台小收割机工作2小时收割小麦3.6公顷;3台大收割机和2台小收割机工作5小时收割小麦8公顷。1台大收割机和1台小收割机工作1小时各收割小麦多少公顷?解: 由题意得 2(2x+ 5y) = 3.65(3x + 2y) = 8 解:去括号,得:②①② - ①,得解这个方程得因此,这个方程组的解是答:1台大收割机1小时收割小麦0.4公顷,1台小收割机1小时收割小麦0.2公顷.小结1.加减消元法的含义是什么? 答:将方程组中两个方程的左、右两边分别相加(或相减),消去其中的一个未知数,将二元一次方程组转化为一元一次方程的方法叫加减消元法,简称加减法二元一次方程组一元一次方程加减消元小结2.加减消元法需满足的条件是什么? 答:相同的未知数中,有一个未知数的系数互为相反数(采用加法),或者有一个未知数的系数相等(采用减法),二者必须满足一个。小结3.加减消元法条件不满足怎么办? 如果同一个未知数的系数既不互为相反数又不相等,就用适当的数去乘方程的两边,使一个未知数的系数互为相反数或相等.灵活运用问题5 怎样解下面的方程组?追问1 第一个方程组选择哪种方法更简便?第二个方程组选择哪种方法更简便?追问2 我们依据什么来选择更简便的方法?灵活运用解:选择代入法,由①得,②①代入②,消去y,解得代入③,得③是原方程组的解.灵活运用解:选择加减法,
①+②得②①代入①,得是原方程组的解.练习①②③代入法加减法解:由①得将③代入②,得代入③,得解:①×4-② ,得代入①,得补偿提高: 【问题4】某工厂第一车间工人人数比第二车间工人人数的2倍少10人,若从第一车间抽调5人到第二车间,那么两个车间的人数一样多. 问原来每个车间各有多少名工人?①第一车间工人人数=第二车间工人人数×2-10;相等关系:②第一车间工人人数-5=第二车间工人人数+5.解:设第一车间原有工人 名,第二车间原有工人 名,
根据题意,得 解这个方程组,得 答:第一车间原有工人30名,第二车间原有工人20名.二元一次方程 2x+y=8有多少个解?请写出它的正整数解注意:一般地,二元一次方程有无数个解。但在实际问题中经常会遇到求方程的正整数解。解:变形:x=8-2y
正整数解是(自然数解)2、方程组与方程组②①的解相同,求m,n的值解:解得?íì=-=+48n2mn=2y=1把=2y=1代入得2mì解得=3.已知:方程组 甲由于看错了a,解得 乙看了错b解得 , 求原方程组正确的解拓广探索4.在x2+ax+b中,当x=2时,其值为3;
当x=-3时,其值为4,求a-b的值解:当x=2时,其值为3,得:
22+2a+b=3
2a+b=-1 ①
当x=-3时,其值为4,得;
(-3)2-3a+b=4
-3a+b=-5 ②
a-b=4/5-(-13/5)=17/55.关于x、y的方程组的解x与y的值相等,试求k的值。解:由已知得:x=y ③
③ 代入①:4x-3x=2
x=2
x=y=2 ① 把x=y=2代入②得:
2k+2(k-1)=6
2k+2k-2=6
4k=8
k=2②变形:关于x、y的方程组的解x与y互为相反数,试求k的值。6.如果关于X,Y的方程组的解是二元一次方程 的一个解,那么m的值是 。练习方程组的应用(1)3x2a+b+2+5y3a-b+1=8是关于x、y的二元一次方程
求a、b11(2)已知(3m+2n-16)2与|3m-n-1|互为相反数. 求:m+n的值解:根据题意:得
(3m+2n-16)2+|3m-n-1|=03m+2n-16=03m-n-1=0即:m+n=7相关题:若(3a+b+5)2+(2a-2b-2)2=0,
则2a2 - 3ab的值为____.作业1、课本P-96 练习
P-98(习题8.2) 3
并尝试一下能否求出它的解问题 观察方程组中的两个方程,未知数y的系数相等。把两个方程两边分别相减,就可以消去未知数y,得到一个一元一次方程。 即?-?,消去未知数y,得 x=6
把x=6代入? ,得 y=4
3x+10y=2.8 ①
15x-10 y=8 ② 观察方程组中的两个方程,未知数y的系数相反。把两个方程两边分别相加,就可以消去未知数y,同样得到一个一元一次方程。分析:举一反三解方程组解:把 ②+①得: 18x=10.8
x=0.6把x=0.6代入①,得:
3×0.6+10y=2.8解得:y=0.1举一反三3x+10y=2.8 ①
15x-10 y=8 ②
分析: 3x+5y +2x - 5y=10 ①左边 + ② 左边 = ① 右边 + ②右边5x =10
x=2(3x + 5y)+(2x - 5y)=21 + (-11)等式性质解:由①+②得: 5x=10 把x=2代入①,得: y=3 x=2新思路 新体验加减消元法 两个二元一次方程中同一未知数的系数相反或相等时,将两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法.由①+②得: 5x=10 x+y=10 ①
2x+y=16 ②由 ②-①得:x=6分别相加y1.已知方程组x+3y=172x-3y=6两个方程就可以消去未知数分别相减2.已知方程组25x-7y=1625x+6y=10两个方程就可以消去未知数x一.填空题:只要两边只要两边练习二.选择题B2.方程组3x+2y=133x-2y=5消去y后所得的方程是( )BA.6x=8B.6x=18C.6x=5D.x=18 三.指出下列方程组求解过程中有错误步骤,并给予订正:7x-4y=4
5x-4y=-4
解:①-②,得
2x=4-4,
x=0
①①②②3x-4y=14
5x+4y=2
解 ①-②,得
-2x=12
x =-6解: ①-②,得
2x=4+4,
x=4解: ①+②,得
8x=16
x =2
看看你掌握了吗? 上面这些方程组的特点是什么?
解这类方程组基本思路是什么?
主要步骤有哪些?想一想,议一议:主要步骤:
特点:基本思路:写解求解加减二元一元加减消元:消去一个元分别求出两个未知数的值写出原方程组的解同一个未知数的系数相同或互为相反数解方程本例题可以用加减
消元法来做吗?
问题1.这两个方程直接相加减能消去未知数吗?为什么? 问题2.那么怎样使方程组中某一未知数系数的绝对值相等呢?
分 析: 对于当方程组中两方程不具备上述特点时,则可用等式性质来改变方程组中方程的形式,即得到与原方程组同解的且某未知数系数的绝对值相等的新的方程组,从而为加减消元法解方程组创造条件.应用新知3x+4y=165x-6y=33二
元
一
次
方
程
组15x+20y=8015x-18y=9938y=-19x=6解得y代入3x+4y=16②×3使未知数x系数相等①×5两式相减消
x解得x解方程组:解法一:① ×3 得 19x = 114 把x = 6代入①得所以这个方程组的解为 即 x = 618 + 4y = 169x+ 12y = 48 ② ×2 得10x - 12y = 66 ③ + ④ 得即 y = ④ ③①②解方程组:解法二:① ×5 得 38y = -19 即 x = 615x+ 20y = 80 ② ×3 得15x - 18y = 99 ③ - ④ 得④ ③①②3x-2 = 16所以这个方程组的解为解:由①×6,得2x+3y=4 ③由②×4,得 2x - y=8 ④由③-④得: y= -1所以原方程组
的解是把y= -1代入② ,
解得:②①
补充练习:用加减消元法解方程组:练习:用加减法解方程组:(1)(2)加减法归纳: 用加减法解同一个未知数的系数绝对值不相等的二元一次方程组时,把一个(或两个)方程的两边乘以适当的数,使两个方程中某一未知数的系数绝对值相等,从而化为第一类型方程组求解.
例4 2台大收割机和5台小收割机工作2小时收割小麦3.6公顷;3台大收割机和2台小收割机工作5小时收割小麦8公顷。1台大收割机和1台小收割机工作1小时各收割小麦多少公顷?解: 大收割机小收割机效率时间工作量xy22台数5(2x+ 5y)2= 3.6创设情境 2台大收割机和5台小收割机工作2小时收割小麦3.6公顷;3台大收割机和2台小收割机工作5小时收割小麦8公顷。1台大收割机和1台小收割机工作1小时各收割小麦多少公顷?解: 大收割机小收割机效率时间工作量xy35台数2(3x+ 2y)5= 8 2台大收割机和5台小收割机工作2小时收割小麦3.6公顷;3台大收割机和2台小收割机工作5小时收割小麦8公顷。1台大收割机和1台小收割机工作1小时各收割小麦多少公顷?解: 由题意得 2(2x+ 5y) = 3.65(3x + 2y) = 8 解:去括号,得:②①② - ①,得解这个方程得因此,这个方程组的解是答:1台大收割机1小时收割小麦0.4公顷,1台小收割机1小时收割小麦0.2公顷.小结1.加减消元法的含义是什么? 答:将方程组中两个方程的左、右两边分别相加(或相减),消去其中的一个未知数,将二元一次方程组转化为一元一次方程的方法叫加减消元法,简称加减法二元一次方程组一元一次方程加减消元小结2.加减消元法需满足的条件是什么? 答:相同的未知数中,有一个未知数的系数互为相反数(采用加法),或者有一个未知数的系数相等(采用减法),二者必须满足一个。小结3.加减消元法条件不满足怎么办? 如果同一个未知数的系数既不互为相反数又不相等,就用适当的数去乘方程的两边,使一个未知数的系数互为相反数或相等.灵活运用问题5 怎样解下面的方程组?追问1 第一个方程组选择哪种方法更简便?第二个方程组选择哪种方法更简便?追问2 我们依据什么来选择更简便的方法?灵活运用解:选择代入法,由①得,②①代入②,消去y,解得代入③,得③是原方程组的解.灵活运用解:选择加减法,
①+②得②①代入①,得是原方程组的解.练习①②③代入法加减法解:由①得将③代入②,得代入③,得解:①×4-② ,得代入①,得补偿提高: 【问题4】某工厂第一车间工人人数比第二车间工人人数的2倍少10人,若从第一车间抽调5人到第二车间,那么两个车间的人数一样多. 问原来每个车间各有多少名工人?①第一车间工人人数=第二车间工人人数×2-10;相等关系:②第一车间工人人数-5=第二车间工人人数+5.解:设第一车间原有工人 名,第二车间原有工人 名,
根据题意,得 解这个方程组,得 答:第一车间原有工人30名,第二车间原有工人20名.二元一次方程 2x+y=8有多少个解?请写出它的正整数解注意:一般地,二元一次方程有无数个解。但在实际问题中经常会遇到求方程的正整数解。解:变形:x=8-2y
正整数解是(自然数解)2、方程组与方程组②①的解相同,求m,n的值解:解得?íì=-=+48n2mn=2y=1把=2y=1代入得2mì解得=3.已知:方程组 甲由于看错了a,解得 乙看了错b解得 , 求原方程组正确的解拓广探索4.在x2+ax+b中,当x=2时,其值为3;
当x=-3时,其值为4,求a-b的值解:当x=2时,其值为3,得:
22+2a+b=3
2a+b=-1 ①
当x=-3时,其值为4,得;
(-3)2-3a+b=4
-3a+b=-5 ②
a-b=4/5-(-13/5)=17/55.关于x、y的方程组的解x与y的值相等,试求k的值。解:由已知得:x=y ③
③ 代入①:4x-3x=2
x=2
x=y=2 ① 把x=y=2代入②得:
2k+2(k-1)=6
2k+2k-2=6
4k=8
k=2②变形:关于x、y的方程组的解x与y互为相反数,试求k的值。6.如果关于X,Y的方程组的解是二元一次方程 的一个解,那么m的值是 。练习方程组的应用(1)3x2a+b+2+5y3a-b+1=8是关于x、y的二元一次方程
求a、b11(2)已知(3m+2n-16)2与|3m-n-1|互为相反数. 求:m+n的值解:根据题意:得
(3m+2n-16)2+|3m-n-1|=03m+2n-16=03m-n-1=0即:m+n=7相关题:若(3a+b+5)2+(2a-2b-2)2=0,
则2a2 - 3ab的值为____.作业1、课本P-96 练习
P-98(习题8.2) 3
