沪教版九年级上《第26章二次函数》单元检测试卷含答案
文档属性
| 名称 | 沪教版九年级上《第26章二次函数》单元检测试卷含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 261.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-24 00:00:00 | ||
图片预览



文档简介
第26章二次函数单元检测卷
姓名:__________ 班级:_________
题号 一 二 三 总分
评分
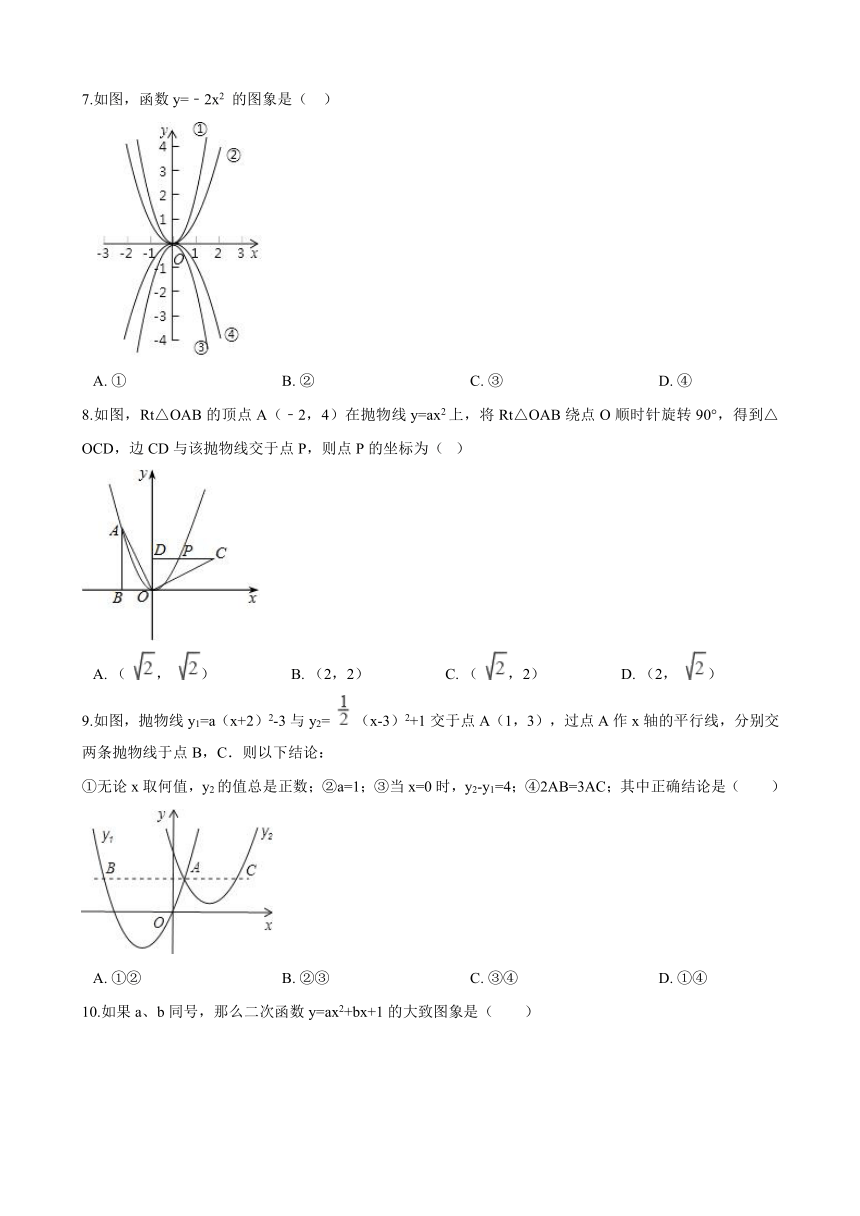
一、选择题(共11小题;每小题3分,共33分)
1.在下列关于x的函数中,一定是二次函数的是( )
A. y=x2 B. y=ax2+bx+c C. y=8x D. y=x2(1+x)
2.二次函数y=x2+2x﹣7的函数值是8,那么对应的x的值是( )
A. 3 B. 5 C. ﹣3和5 D. 3和﹣5
3.抛物线y=a(x+1)(x﹣3)(a≠0)的对称轴是直线( )
A. x=1 B. x=﹣1 C. x=﹣3 D. x=3
4.已知二次函数y=x2+bx+3如图所示,那么函数y=x2+(b﹣1)x+3的图象可能是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
5.若正比例函数y=mx(m≠0),y随x的增大而减小,则它和二次函数y=mx2+m的图象大致是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
6.二次函数y=ax2+bx+c的图象如图所示,则函数值y<0时x的取值范围是( )
( http: / / www.21cnjy.com )
A. x<﹣1 B. x>3 C. ﹣1<x<3 D. x<﹣1或x>3
7.如图,函数y=﹣2x2 的图象是( )
( http: / / www.21cnjy.com )
A. ① B. ② C. ③ D. ④
8.如图,Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )
( http: / / www.21cnjy.com )
A. ( ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )) B. (2,2) C. ( ( http: / / www.21cnjy.com ),2) D. (2, ( http: / / www.21cnjy.com ))
9.如图,抛物线y1=a(x+2)2-3与y2= ( http: / / www.21cnjy.com ) (x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
①无论x取何值,y2的值总是正数;②a=1;③当x=0时,y2-y1=4;④2AB=3AC;其中正确结论是( )
( http: / / www.21cnjy.com )
A. ①② B. ②③ C. ③④ D. ①④
10.如果a、b同号,那么二次函数y=ax2+bx+1的大致图象是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com )
C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
11.函数y=ax2+bx+a+b(a≠0)的图象可能是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
二、填空题(共10题;共3分)
12.方程2x﹣x2= ( http: / / www.21cnjy.com )的正实数根有________ 个
13.点A(﹣3,y1),B(2,y2)在抛物线y=x2﹣5x上,则y1________y2 . (填“>”,“<”或“=”)
14.若函数y=(m+2) ( http: / / www.21cnjy.com )是关于x的二次函数,则满足条件的m的值为________.
15.当m________ 时,y=(m﹣2) ( http: / / www.21cnjy.com )是二次函数.
16.若直线y=m(m为常数)与函数y= ( http: / / www.21cnjy.com )的图象有三个不同的交点,则常数m的取值范围________
17.若y与x的函数 ( http: / / www.21cnjy.com )是二次函数,则________ .
18.若函数y=(m﹣2)x|m|是二次函数,则m=________.
19.如图为函数:y=x2﹣1,y=x2+6x+8,y=x2﹣6x+8,y=x2﹣12x+35在同一平面直角坐标系中的图象,其中最有可能是y=x2﹣6x+8的图象的序号是________.
( http: / / www.21cnjy.com )
20.若函数 ( http: / / www.21cnjy.com )是二次函数,则m的值为________.
21.二次函数y=3x﹣5x2+1的二次项系数、一次项系数、常数项分别为________.
三、解答题(共3题;共37分)
22.用一根长为800cm的木条做一个长方形窗框,若宽为x cm,写出它的面积y与x之间的函数关系式,并判断y是x的二次函数吗?
23.一个二次函数y=(k﹣1) ( http: / / www.21cnjy.com )+2x﹣1.
(1)求k值.
(2)求当x=0.5时y的值?
24.如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,且抛物线经过A(﹣1,0),C(0,﹣5)两点,与x轴交于点B.
( http: / / www.21cnjy.com )
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)设点P为抛物线上的一个动点,连接PB、PC,若△BPC是以BC为直角边的直角三角形,求此时点P的坐标;
(3)在抛物线上BC段有另一个动点Q,以点 ( http: / / www.21cnjy.com )Q为圆心作⊙Q,使得⊙Q与直线BC相切,在运动的过程中是否存在一个最大⊙Q?若存在,请直接写出最大⊙Q的半径;若不存在,请说明理由.
参考答案
一、 选择题
A D A C A C C C D D C
二、填空题
12. 0
13. >
14. 1
15. ﹣2
16. 0<m<4
17. m= ﹣1
18. -2
19. 第三个
20. -3
21. ﹣5、3、1
三、解答题
22. 解:设宽为xcm,
由题意得,矩形的周长为800cm,
∴矩形的长为 ( http: / / www.21cnjy.com )cm,
∴y=x× ( http: / / www.21cnjy.com )=﹣x2+400x(0<x<400).
y是x的二次函数.
23. 解:(1)由题意得:k2﹣3k+4=2,且k﹣1≠0,
解得:k=2;
(2)把k=2代入y=(k﹣1) ( http: / / www.21cnjy.com )+2x﹣1得:y=x2+2x﹣1,
当x=0.5时,y= ( http: / / www.21cnjy.com ).
24. (1)解:∵对称轴为x=2,且抛物线经过A(﹣1,0),
∴B(5,0).
把B(5,0),C(0,﹣5)分别代入y=mx+n得 ( http: / / www.21cnjy.com ),解得: ( http: / / www.21cnjy.com ),
∴直线BC的解析式为y=x﹣5.
设y=a(x﹣5)(x+1),把点C的坐标代入得:﹣5a=﹣5,解得:a=1,
∴抛物线的解析式为:y=x2﹣4x﹣5
(2)解:①过点C作CP1⊥BC,交抛物线于点P1 , 如图,
( http: / / www.21cnjy.com )
则直线CP1的解析式为y=﹣x﹣5,
由 ( http: / / www.21cnjy.com ),解得: ( http: / / www.21cnjy.com )(舍去), ( http: / / www.21cnjy.com ),
∴P1(3,﹣8);
②过点B作BP2⊥BC,交抛物线于P2 , 如图,
( http: / / www.21cnjy.com )
则BP2的解析式为y=﹣x+5,
由 ( http: / / www.21cnjy.com ),解得: ( http: / / www.21cnjy.com )(舍去), ( http: / / www.21cnjy.com ),
∴P2(﹣2,7)
(3)解:由题意可知,Q点距离BC最远时,半径最大.平移直线BC,使其与抛物线只有一个公共点Q(即相切),设平移后的直线解析式为y=x+t,
由 ( http: / / www.21cnjy.com ),消去y整理得x2﹣5x﹣5﹣t=0,
△=25+4(5+t)=0,解得t=﹣ ( http: / / www.21cnjy.com ),
∴平移后与抛物线相切时的直线解析式为y=x﹣ ( http: / / www.21cnjy.com ),且Q( ( http: / / www.21cnjy.com ),﹣ ( http: / / www.21cnjy.com )),
连接QC、QB,作QE⊥BC于E,如图,
( http: / / www.21cnjy.com )
设直线y=x﹣ ( http: / / www.21cnjy.com )与y轴的交点为H,连接HB,
则 ( http: / / www.21cnjy.com ),
∵CH=﹣5﹣(﹣ ( http: / / www.21cnjy.com ))= ( http: / / www.21cnjy.com ),
∴ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴ ( http: / / www.21cnjy.com ),
∵ ( http: / / www.21cnjy.com ),BC= ( http: / / www.21cnjy.com ),
∴QE= ( http: / / www.21cnjy.com ),
即最大半径为 ( http: / / www.21cnjy.com )
姓名:__________ 班级:_________
题号 一 二 三 总分
评分
一、选择题(共11小题;每小题3分,共33分)
1.在下列关于x的函数中,一定是二次函数的是( )
A. y=x2 B. y=ax2+bx+c C. y=8x D. y=x2(1+x)
2.二次函数y=x2+2x﹣7的函数值是8,那么对应的x的值是( )
A. 3 B. 5 C. ﹣3和5 D. 3和﹣5
3.抛物线y=a(x+1)(x﹣3)(a≠0)的对称轴是直线( )
A. x=1 B. x=﹣1 C. x=﹣3 D. x=3
4.已知二次函数y=x2+bx+3如图所示,那么函数y=x2+(b﹣1)x+3的图象可能是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
5.若正比例函数y=mx(m≠0),y随x的增大而减小,则它和二次函数y=mx2+m的图象大致是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
6.二次函数y=ax2+bx+c的图象如图所示,则函数值y<0时x的取值范围是( )
( http: / / www.21cnjy.com )
A. x<﹣1 B. x>3 C. ﹣1<x<3 D. x<﹣1或x>3
7.如图,函数y=﹣2x2 的图象是( )
( http: / / www.21cnjy.com )
A. ① B. ② C. ③ D. ④
8.如图,Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )
( http: / / www.21cnjy.com )
A. ( ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )) B. (2,2) C. ( ( http: / / www.21cnjy.com ),2) D. (2, ( http: / / www.21cnjy.com ))
9.如图,抛物线y1=a(x+2)2-3与y2= ( http: / / www.21cnjy.com ) (x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
①无论x取何值,y2的值总是正数;②a=1;③当x=0时,y2-y1=4;④2AB=3AC;其中正确结论是( )
( http: / / www.21cnjy.com )
A. ①② B. ②③ C. ③④ D. ①④
10.如果a、b同号,那么二次函数y=ax2+bx+1的大致图象是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com )
C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
11.函数y=ax2+bx+a+b(a≠0)的图象可能是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
二、填空题(共10题;共3分)
12.方程2x﹣x2= ( http: / / www.21cnjy.com )的正实数根有________ 个
13.点A(﹣3,y1),B(2,y2)在抛物线y=x2﹣5x上,则y1________y2 . (填“>”,“<”或“=”)
14.若函数y=(m+2) ( http: / / www.21cnjy.com )是关于x的二次函数,则满足条件的m的值为________.
15.当m________ 时,y=(m﹣2) ( http: / / www.21cnjy.com )是二次函数.
16.若直线y=m(m为常数)与函数y= ( http: / / www.21cnjy.com )的图象有三个不同的交点,则常数m的取值范围________
17.若y与x的函数 ( http: / / www.21cnjy.com )是二次函数,则________ .
18.若函数y=(m﹣2)x|m|是二次函数,则m=________.
19.如图为函数:y=x2﹣1,y=x2+6x+8,y=x2﹣6x+8,y=x2﹣12x+35在同一平面直角坐标系中的图象,其中最有可能是y=x2﹣6x+8的图象的序号是________.
( http: / / www.21cnjy.com )
20.若函数 ( http: / / www.21cnjy.com )是二次函数,则m的值为________.
21.二次函数y=3x﹣5x2+1的二次项系数、一次项系数、常数项分别为________.
三、解答题(共3题;共37分)
22.用一根长为800cm的木条做一个长方形窗框,若宽为x cm,写出它的面积y与x之间的函数关系式,并判断y是x的二次函数吗?
23.一个二次函数y=(k﹣1) ( http: / / www.21cnjy.com )+2x﹣1.
(1)求k值.
(2)求当x=0.5时y的值?
24.如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,且抛物线经过A(﹣1,0),C(0,﹣5)两点,与x轴交于点B.
( http: / / www.21cnjy.com )
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)设点P为抛物线上的一个动点,连接PB、PC,若△BPC是以BC为直角边的直角三角形,求此时点P的坐标;
(3)在抛物线上BC段有另一个动点Q,以点 ( http: / / www.21cnjy.com )Q为圆心作⊙Q,使得⊙Q与直线BC相切,在运动的过程中是否存在一个最大⊙Q?若存在,请直接写出最大⊙Q的半径;若不存在,请说明理由.
参考答案
一、 选择题
A D A C A C C C D D C
二、填空题
12. 0
13. >
14. 1
15. ﹣2
16. 0<m<4
17. m= ﹣1
18. -2
19. 第三个
20. -3
21. ﹣5、3、1
三、解答题
22. 解:设宽为xcm,
由题意得,矩形的周长为800cm,
∴矩形的长为 ( http: / / www.21cnjy.com )cm,
∴y=x× ( http: / / www.21cnjy.com )=﹣x2+400x(0<x<400).
y是x的二次函数.
23. 解:(1)由题意得:k2﹣3k+4=2,且k﹣1≠0,
解得:k=2;
(2)把k=2代入y=(k﹣1) ( http: / / www.21cnjy.com )+2x﹣1得:y=x2+2x﹣1,
当x=0.5时,y= ( http: / / www.21cnjy.com ).
24. (1)解:∵对称轴为x=2,且抛物线经过A(﹣1,0),
∴B(5,0).
把B(5,0),C(0,﹣5)分别代入y=mx+n得 ( http: / / www.21cnjy.com ),解得: ( http: / / www.21cnjy.com ),
∴直线BC的解析式为y=x﹣5.
设y=a(x﹣5)(x+1),把点C的坐标代入得:﹣5a=﹣5,解得:a=1,
∴抛物线的解析式为:y=x2﹣4x﹣5
(2)解:①过点C作CP1⊥BC,交抛物线于点P1 , 如图,
( http: / / www.21cnjy.com )
则直线CP1的解析式为y=﹣x﹣5,
由 ( http: / / www.21cnjy.com ),解得: ( http: / / www.21cnjy.com )(舍去), ( http: / / www.21cnjy.com ),
∴P1(3,﹣8);
②过点B作BP2⊥BC,交抛物线于P2 , 如图,
( http: / / www.21cnjy.com )
则BP2的解析式为y=﹣x+5,
由 ( http: / / www.21cnjy.com ),解得: ( http: / / www.21cnjy.com )(舍去), ( http: / / www.21cnjy.com ),
∴P2(﹣2,7)
(3)解:由题意可知,Q点距离BC最远时,半径最大.平移直线BC,使其与抛物线只有一个公共点Q(即相切),设平移后的直线解析式为y=x+t,
由 ( http: / / www.21cnjy.com ),消去y整理得x2﹣5x﹣5﹣t=0,
△=25+4(5+t)=0,解得t=﹣ ( http: / / www.21cnjy.com ),
∴平移后与抛物线相切时的直线解析式为y=x﹣ ( http: / / www.21cnjy.com ),且Q( ( http: / / www.21cnjy.com ),﹣ ( http: / / www.21cnjy.com )),
连接QC、QB,作QE⊥BC于E,如图,
( http: / / www.21cnjy.com )
设直线y=x﹣ ( http: / / www.21cnjy.com )与y轴的交点为H,连接HB,
则 ( http: / / www.21cnjy.com ),
∵CH=﹣5﹣(﹣ ( http: / / www.21cnjy.com ))= ( http: / / www.21cnjy.com ),
∴ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴ ( http: / / www.21cnjy.com ),
∵ ( http: / / www.21cnjy.com ),BC= ( http: / / www.21cnjy.com ),
∴QE= ( http: / / www.21cnjy.com ),
即最大半径为 ( http: / / www.21cnjy.com )
