沪教版九年级下册数学《第27章圆与正多边形》单元检测试卷含答案
文档属性
| 名称 | 沪教版九年级下册数学《第27章圆与正多边形》单元检测试卷含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 234.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-24 16:05:06 | ||
图片预览



文档简介
第27章圆与正多边形单元检测卷 姓名:__________ 班级:_________
题号
一
二
三
总分
评分
?
?
?
?
一、选择题(共12小题;每小题3分,共36分)
1.下列说法正确的是(?? )
A.平分弦的直径垂直于弦 B.三点确定一个圆 C.相等的圆心角所对弦相等 D.直径为圆中最长的弦
2.如图,已知⊙O的周长为4π,的长为π,则图中阴影部分的面积为( )
A.?π﹣2???????????????????????????????????????B.????????????????????????????????????????C.?π???????????????????????????????????????D.?2
3. 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB= ,则AB的长是(?? )
A.?4????????????????????????????????????????B.?2 ????????????????????????????????????????C.?8????????????????????????????????????????D.?4
4.已知两圆的半径分别为2和3,圆心距为5,则这两圆的位置关系是(??)
A.?外离?????????????????????????????????????B.?外切?????????????????????????????????????C.?相交?????????????????????????????????????D.?内切
5.如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”.则半径为2的“等边扇形”的面积为(????)?
A.?π??????????????????????????????????????????B.?1??????????????????????????????????????????C.?2??????????????????????????????????????????D.?
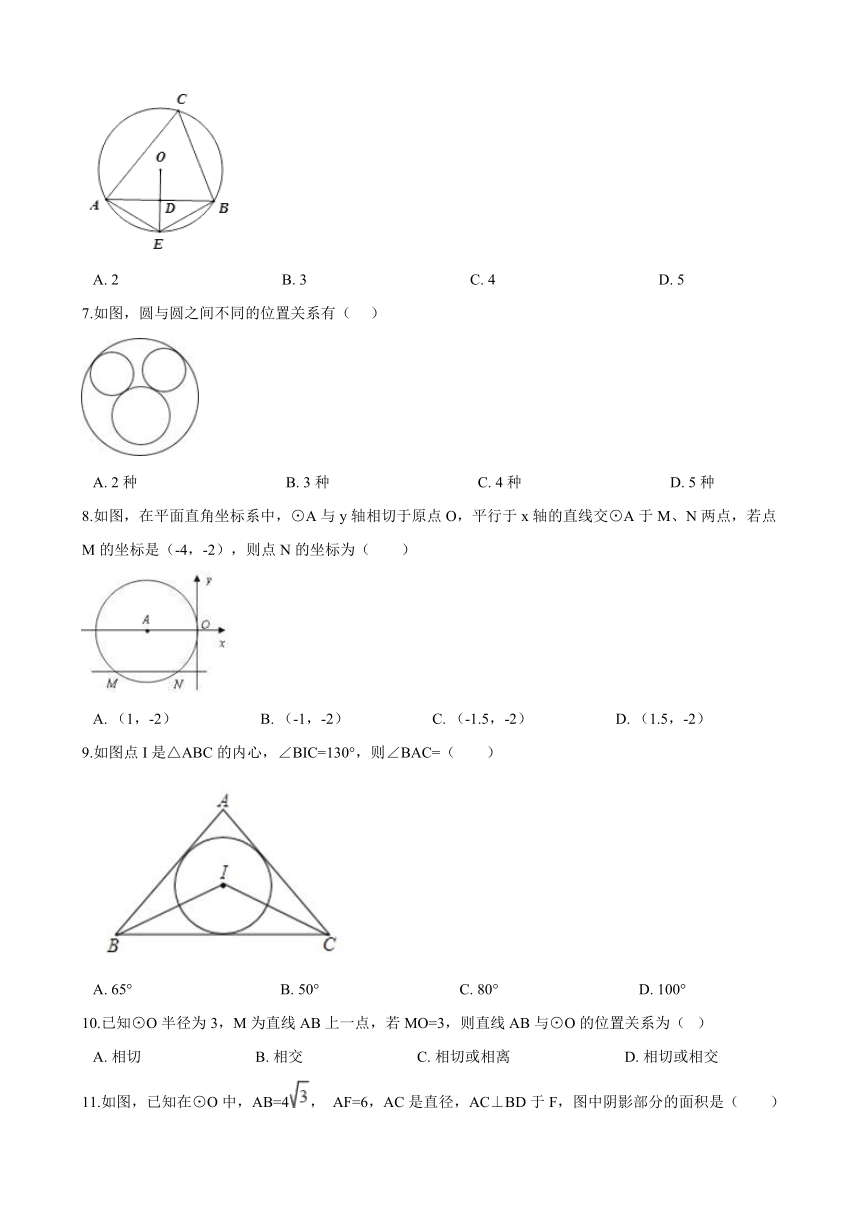
6.如图,△ABC内接于⊙O,D为线段AB的中点,延长OD交⊙O于点E,连接AE,BE,则下列五个结论①AB⊥DE,? ②AE=BE , ③OD=DE, ④∠AEO=∠C, ⑤弧AE=弧AEB,正确结论的个数是( )
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
7.如图,圆与圆之间不同的位置关系有(??? )
A.?2种???????????????????????????????????????B.?3种???????????????????????????????????????C.?4种???????????????????????????????????????D.?5种
8.如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点,若点M的坐标是(-4,-2),则点N的坐标为( )
A.?(1,-2)??????????????????????B.?(-1,-2)??????????????????????C.?(-1.5,-2)??????????????????????D.?(1.5,-2)
9.如图点I是△ABC的内心,∠BIC=130°,则∠BAC=( )
A.?65°???????????????????????????????????????B.?50°?????????????????????????????????????C.?80°?????????????????????????????????????D.?100°
10.已知⊙O半径为3,M为直线AB上一点,若MO=3,则直线AB与⊙O的位置关系为(? )
A.?相切??????????????????????????????B.?相交??????????????????????????????C.?相切或相离??????????????????????????????D.?相切或相交
11.如图,已知在⊙O中,AB=4, AF=6,AC是直径,AC⊥BD于F,图中阴影部分的面积是( )
A.??????????????????????????B.??????????????????????????C.??????????????????????????D.?
12.如图,A,B是⊙O的直径,C、D在⊙O上,, 若∠DAB=58°,则∠CAB=( )
A.?20°???????????????????????????????????????B.?22°???????????????????????????????????????C.?24°???????????????????????????????????????D.?26°
二、填空题(共10题;30分)
13.如图,扇形OAB的圆心角为120°,半径为3cm,则该扇形的弧长为________?cm,面积为________?cm2 . (结果保留π)
14.已知⊙O是以坐标原点为圆心,半径为1,函数y=x与⊙O交与点A、B,点P(x,0)在x轴上运动,过点P且与OA平行的直线与⊙O有公共点,则x的范围是________ .
15.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为________.
16.半径为5cm的圆中有两条平行弦,长度分别为6cm和8cm,则这两条弦的距离为________?。
17.圆上各点到圆心的距离都等于________?,到圆心距离等于半径的点都在________?.
18.扇形的圆心角为120°,弧长为6πcm,那么这个扇形的面积为________?cm2 .
19.如图,AB切⊙O于点B,BC∥OA,交⊙O于点C,若∠OAB=30°,BC=6,则劣弧BC的长为________.
20.如图,已知⊙P的半径为2,圆心P在抛物线y=x2﹣1上运动,当⊙P与x轴相切时,圆心P的坐标为?________.
21. 如图,⊙O的半径为2,点A、C在⊙O上,线段BD经过圆心O,∠ABD=∠CDB=90°,AB=1,CD= ,则图中阴影部分的面积为________.
22.已知AB是⊙O的直径,弦CD⊥AB于点E,如果AB=8,CD=6,那么OE=________?
三、解答题(共4题;34分)
23.如图,在⊙O中,AB为弦,C、D在AB上,且AC=BD,请问图中有几个等腰三角形?把它们分别写出来,并说明理由. ?
24.如图,在梯形ABCD中,AB∥CD,⊙O为内切圆,E为切点.若AO=8cm,DO=6cm,求OE的长.
25.如图,在平面直角坐标系中,点P的坐标为(-4,0),⊙P的半径为2,将⊙P沿x轴向右平移4个单位得到⊙P1. (1)画出⊙P1 , 并直接判断⊙P与⊙P1的位置关系. (2)设⊙P1与x轴正半轴,y轴正半轴的交点分别为A、B,求劣弧AB与弦AB围成的图形的面积.(结果保留π)
26.如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
参考答案
一、选择题
D A C B C B C B C D D D
二、填空题
13. 2π;3π
14. ≤x≤
15. 44
16. 1cm或7cm
17. 圆的半径;圆上
18. 27π
19. 2π
20. (, 2)或(﹣, 2)
21.
22.
三、解答题
23. 解:等腰三角形有:△OAB、△OCD. 证明:∵OA=OB(同圆半径相等), ∴△OAB是等腰三角形, ∴∠A=∠B, 又∵AC=BD,OA=OB, ∴△OAC≌△OBD, ∴OC=OD, ∴△OCD是等腰三角形.
24. 解:∵AB∥CD,⊙O为内切圆, ∴∠OAD+∠ODA=90°, ∴∠AOD=90°, ∵AO=8cm,DO=6cm, ∴AD=10cm, ∵OE⊥AD, ∴AD?OE=OD?OA, ∴OE=4.8cm.
25. 解:(1)⊙P1的位置如图所示,它与⊙P的位置关系为外切. (2)S扇形OAB=π×22=π,S△AOB=×2×2=2. ∴劣弧AB与弦AB围成的图形的面积为:π-2.
26. (1)证明:连接OD,与AF相交于点G, ∵CE与⊙O相切于点D, ∴OD⊥CE, ∴∠CDO=90°, ∵AD∥OC, ∴∠ADO=∠DOC,∠DAO=∠BOC, ∵OA=OD, ∴∠ADO=∠DAO, ∴∠DOC=∠BOC, 在△CDO和△CBO中, , ∴△CDO≌△CBO, ∴∠CBO=∠CDO=90°, ∴CB是⊙O的切线 (2)证明:由(1)可知∠DOA=∠BCO,∠DOC=∠BOC, ∵∠ECB=60°, ∴∠DCO=∠BCO= ∠ECB=30°, ∴∠DOC=∠BOC=60°, ∴∠DOA=60°, ∵OA=OD, ∴△OAD是等边三角形, ∴AD=OD=OF,∵∠GOF=∠ADO, 在△ADG和△FOG中, , ∴△ADG≌△FOG, ∴S△ADG=S△FOG , ∵AB=6, ∴⊙O的半径r=3, ∴S阴=S扇形ODF= = π.
