17.1 勾股定理 课件
图片预览





文档简介
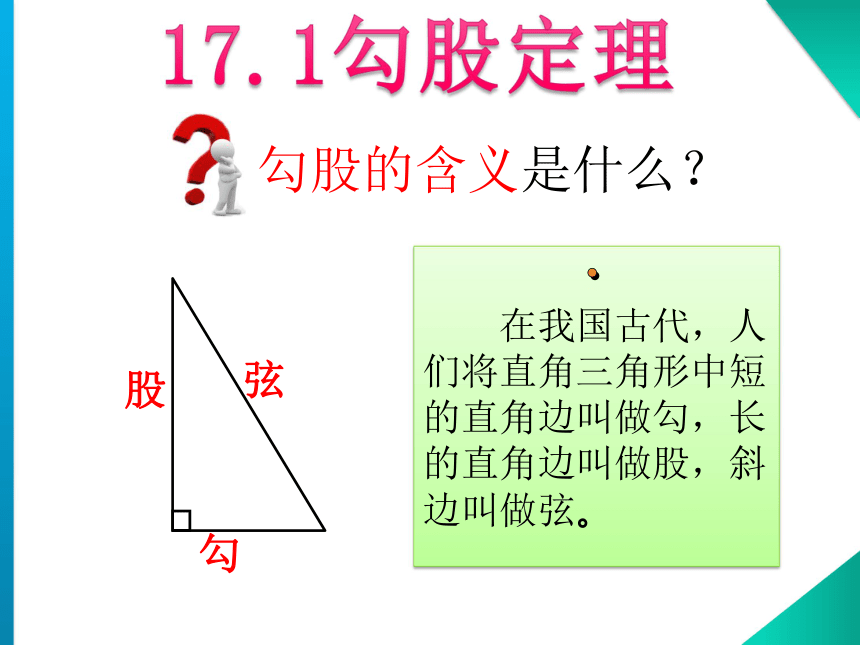
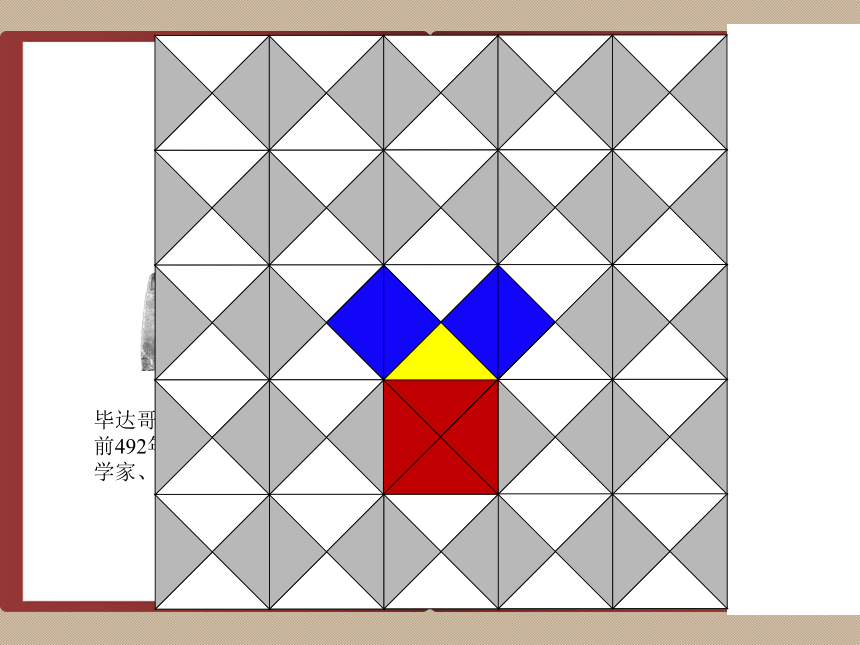
课件35张PPT。勾股定理17.1勾股定理勾股弦勾股的含义是什么?2002年第24届国际数学家大会数学界的“奥运会” 相传2500年前,毕达哥拉斯有
一次在朋友家做客时,发现朋友家
的用砖铺成的地面中反映了直角三
角形三边的某种数量关系。 相传2500年前,毕达哥拉斯有
一次在朋友家做客时,发现朋友家
的用砖铺成的地面中反映了直角三
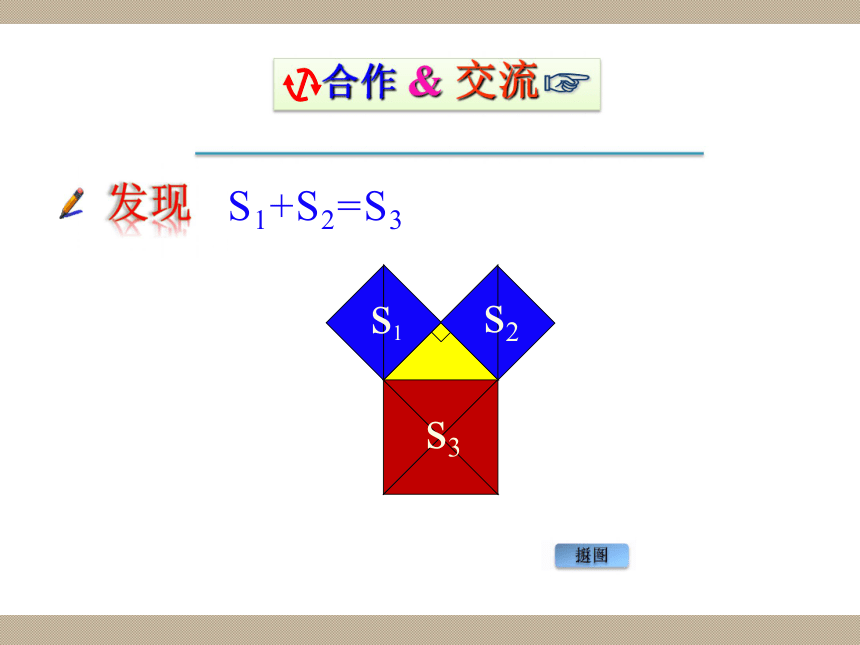
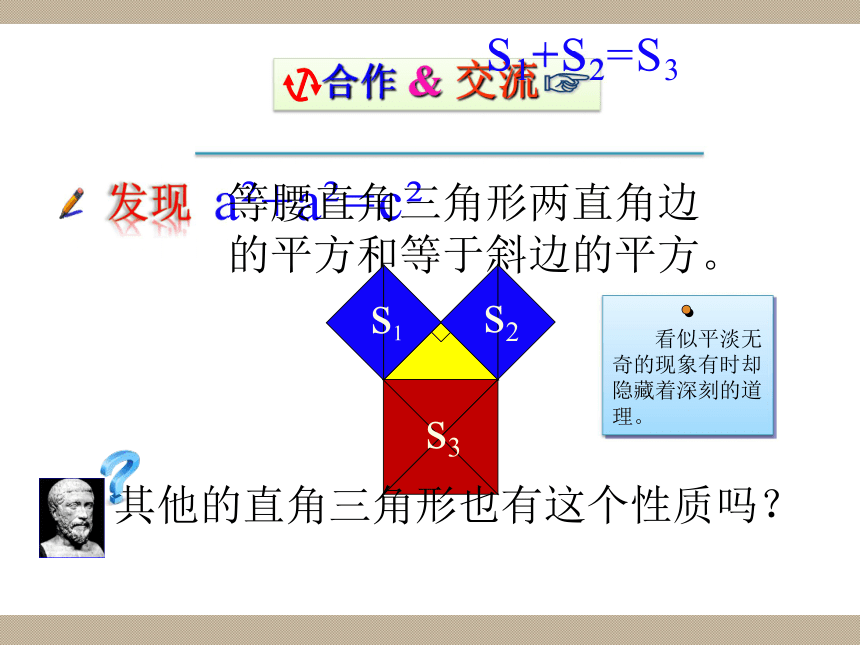
角形三边的某种数量关系。S1+S2=S3发现返回拼图s1s2s3S1+S2=S3aaca2+a2=c2等腰直角三角形两直角边
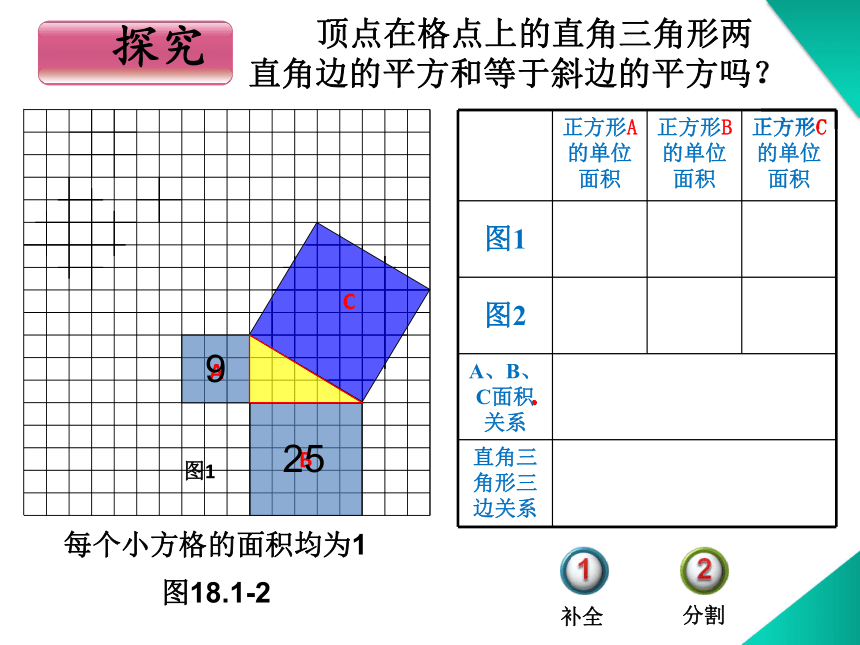
的平方和等于斜边的平方。发现其他的直角三角形也有这个性质吗? 顶点在格点上的直角三角形两
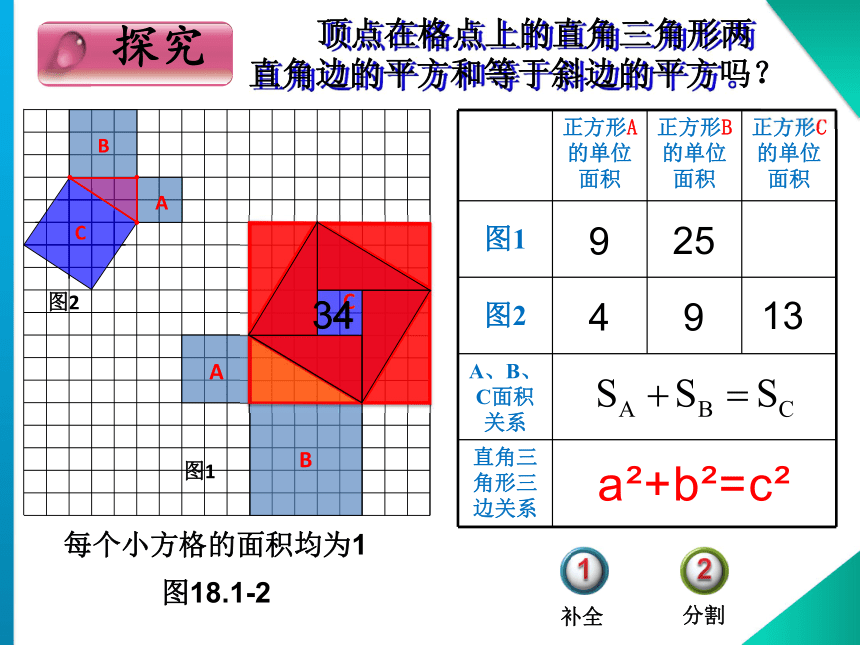
直角边的平方和等于斜边的平方吗?图18.1-2每个小方格的面积均为1ABC图19252分割补全探究探究图18.1-2每个小方格的面积均为1ABC图1925分割补全34ABC图24913a2+b2=c2 顶点在格点上的直角三角形两
直角边的平方和等于斜边的平方。 顶点在格点上的直角三角形两
直角边的平方和等于斜边的平方吗? 命题1 如果直角三角形的两直角边长
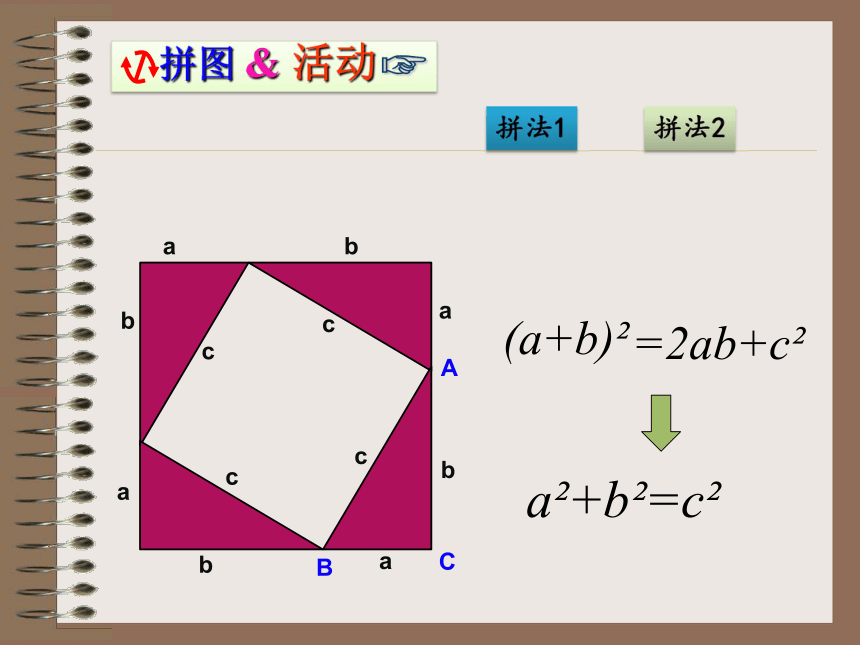
分别为a,b,斜边长为c,那么a2+b2=c2 。由上面的例子,我们猜想:17.1勾股定理返回主界面 拼法1拼法21、拿出准备好的四个全等的直角三角形
(设两条直角边分别为a,b,斜边为c);2、小组合作用这四个直角三角形拼成一个
正方形吗?拼一拼试试看;3、能否就拼出的图说明a2+b2=c2 ? 2ab+c2(a+b)2=a2+b2=c2ABCcababcbabacc拼法1拼法2 朱实ABCcab朱实朱实朱实黄实2ab+(b-a)2=c2a2+b2=c2abcC返回主界面 拼法1拼法2 赵
爽弦 图返回主界面 赵爽是3世纪我国汉代的
数学家与天文学家,他在注解
《周髀算经》时,用他画的弦
图来证明了上面的命题。下面
我们就来看看他是怎样证明的。
赵爽是3世纪我国汉代的
数学家与天文学家,他在注解
《周髀算经》时,用他画的弦
图来证明了上面的命题。下面
我们就来看看他是怎样证明的。
b2a2S=a2+b2赵 爽 证 法S=a2+b2赵 爽 证 法cabcba赵 爽 证 法剪拼abbacccc剪拼返回赵 爽 证 法S=a2+b2S=c2a2+b2=c2赵 爽 证 法返回主界面 1448136100看图求出边长为 的值。 巩固 提高 拓展 返回主界面 ???68351312求下面直角三角形中未知边的长。 巩固 提高 拓展 返回主界面 蚂
蚁
找
食
物 巩固 提高 拓展每个小正方形的边长为1cm画出蚂蚁
经过草莓
并回到窝
的最短路
线图。并
计算出路
线长度。 画图 提示列式4cm4cm6cm4cm x2=42+42
x2=32x cmy cm y2=62+42
y2=52 计算 返回主界面 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。人们对勾股定理的证明颇感兴趣,因为这个定理太贴近人们的生活,下面让我们一起来了解有关于勾股定理及其证明的一些课外知识。延伸1延伸2延伸3延伸4 返回主界面 假如我们一旦和外星人见面,该使用什么语言呢?中国数学家华罗庚认为,我们可以用两个图形作为与外星人交谈的媒介,一个是“数”,另一个是“数形关系”(勾股定理)。因为这种自然图形所具备的“数形关系”在整个宇宙中是普遍的。延伸1延伸2延伸3延伸4 返回主界面 神
奇
的
毕
达
哥
拉
斯
树延伸1延伸2延伸3延伸4 返回主界面 出入相补刘徽(生于公元三世纪)
三国魏晋时代人。
魏景元四年(即 263 年)为古籍《九章算术》作注释。
在注作中,提出以“出入相补”的原理来证明“勾股定理”。后人称该图为“青朱入出图”。延伸1延伸2延伸3延伸4 ……….. abc青
朱
出
入
图延伸1延伸2延伸4 返回主界面 延伸3 美国总统的证明加菲尔德( 1831 ? 1881)
1881 年成为美国第 20 任总统
1876 年提出有关证明
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把他的证法称为“总统”证法。延伸1延伸2延伸3延伸4 aabbcc延伸1延伸2延伸3延伸4 返回主界面 “今天,我学到了……”你说,我说,大家说!返回主界面 作业布置1、课本69页习题18.1第1题。2、阅读课本71页选学内容,并收集一些勾股定理的证明方法。3、做一棵奇妙的勾股树。(选做)返回主界面
一次在朋友家做客时,发现朋友家
的用砖铺成的地面中反映了直角三
角形三边的某种数量关系。 相传2500年前,毕达哥拉斯有
一次在朋友家做客时,发现朋友家
的用砖铺成的地面中反映了直角三
角形三边的某种数量关系。S1+S2=S3发现返回拼图s1s2s3S1+S2=S3aaca2+a2=c2等腰直角三角形两直角边
的平方和等于斜边的平方。发现其他的直角三角形也有这个性质吗? 顶点在格点上的直角三角形两
直角边的平方和等于斜边的平方吗?图18.1-2每个小方格的面积均为1ABC图19252分割补全探究探究图18.1-2每个小方格的面积均为1ABC图1925分割补全34ABC图24913a2+b2=c2 顶点在格点上的直角三角形两
直角边的平方和等于斜边的平方。 顶点在格点上的直角三角形两
直角边的平方和等于斜边的平方吗? 命题1 如果直角三角形的两直角边长
分别为a,b,斜边长为c,那么a2+b2=c2 。由上面的例子,我们猜想:17.1勾股定理返回主界面 拼法1拼法21、拿出准备好的四个全等的直角三角形
(设两条直角边分别为a,b,斜边为c);2、小组合作用这四个直角三角形拼成一个
正方形吗?拼一拼试试看;3、能否就拼出的图说明a2+b2=c2 ? 2ab+c2(a+b)2=a2+b2=c2ABCcababcbabacc拼法1拼法2 朱实ABCcab朱实朱实朱实黄实2ab+(b-a)2=c2a2+b2=c2abcC返回主界面 拼法1拼法2 赵
爽弦 图返回主界面 赵爽是3世纪我国汉代的
数学家与天文学家,他在注解
《周髀算经》时,用他画的弦
图来证明了上面的命题。下面
我们就来看看他是怎样证明的。
赵爽是3世纪我国汉代的
数学家与天文学家,他在注解
《周髀算经》时,用他画的弦
图来证明了上面的命题。下面
我们就来看看他是怎样证明的。
b2a2S=a2+b2赵 爽 证 法S=a2+b2赵 爽 证 法cabcba赵 爽 证 法剪拼abbacccc剪拼返回赵 爽 证 法S=a2+b2S=c2a2+b2=c2赵 爽 证 法返回主界面 1448136100看图求出边长为 的值。 巩固 提高 拓展 返回主界面 ???68351312求下面直角三角形中未知边的长。 巩固 提高 拓展 返回主界面 蚂
蚁
找
食
物 巩固 提高 拓展每个小正方形的边长为1cm画出蚂蚁
经过草莓
并回到窝
的最短路
线图。并
计算出路
线长度。 画图 提示列式4cm4cm6cm4cm x2=42+42
x2=32x cmy cm y2=62+42
y2=52 计算 返回主界面 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。人们对勾股定理的证明颇感兴趣,因为这个定理太贴近人们的生活,下面让我们一起来了解有关于勾股定理及其证明的一些课外知识。延伸1延伸2延伸3延伸4 返回主界面 假如我们一旦和外星人见面,该使用什么语言呢?中国数学家华罗庚认为,我们可以用两个图形作为与外星人交谈的媒介,一个是“数”,另一个是“数形关系”(勾股定理)。因为这种自然图形所具备的“数形关系”在整个宇宙中是普遍的。延伸1延伸2延伸3延伸4 返回主界面 神
奇
的
毕
达
哥
拉
斯
树延伸1延伸2延伸3延伸4 返回主界面 出入相补刘徽(生于公元三世纪)
三国魏晋时代人。
魏景元四年(即 263 年)为古籍《九章算术》作注释。
在注作中,提出以“出入相补”的原理来证明“勾股定理”。后人称该图为“青朱入出图”。延伸1延伸2延伸3延伸4 ……….. abc青
朱
出
入
图延伸1延伸2延伸4 返回主界面 延伸3 美国总统的证明加菲尔德( 1831 ? 1881)
1881 年成为美国第 20 任总统
1876 年提出有关证明
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把他的证法称为“总统”证法。延伸1延伸2延伸3延伸4 aabbcc延伸1延伸2延伸3延伸4 返回主界面 “今天,我学到了……”你说,我说,大家说!返回主界面 作业布置1、课本69页习题18.1第1题。2、阅读课本71页选学内容,并收集一些勾股定理的证明方法。3、做一棵奇妙的勾股树。(选做)返回主界面
