17.1 勾股定理 课件
图片预览



文档简介
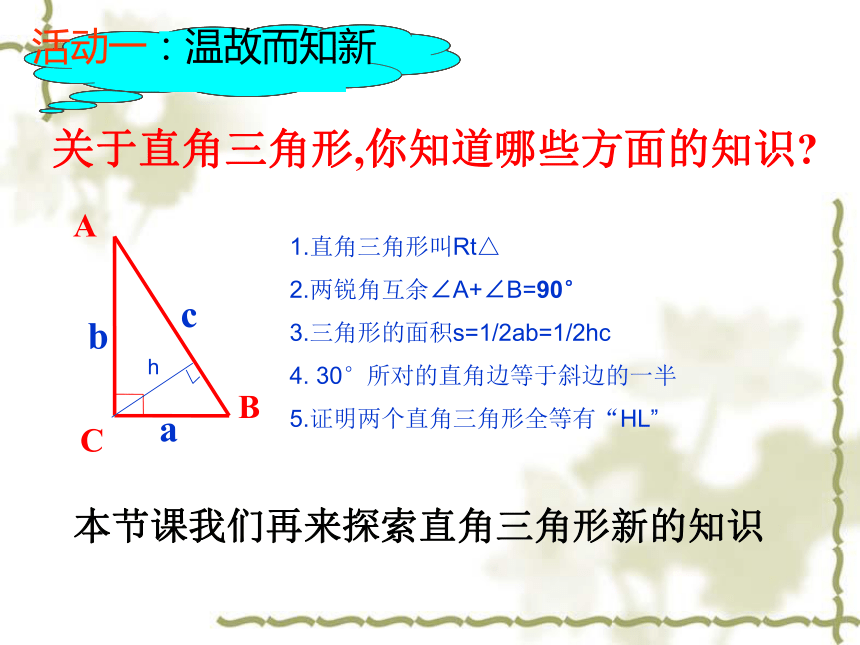
课件26张PPT。探索勾股定理八年级数学关于直角三角形,你知道哪些方面的知识?1.直角三角形叫Rt△
2.两锐角互余∠A+∠B=90°
3.三角形的面积s=1/2ab=1/2hc
4. 30°所对的直角边等于斜边的一半
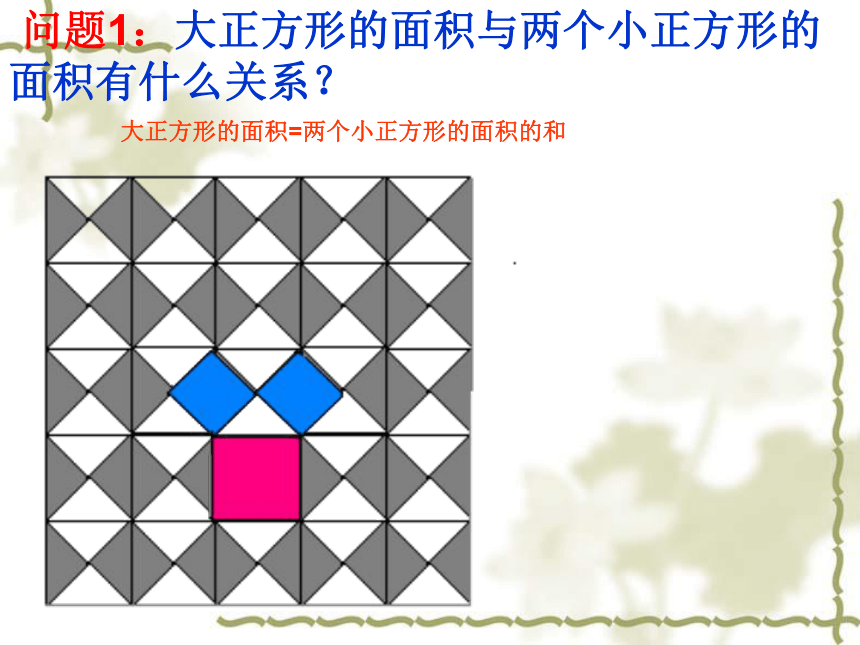
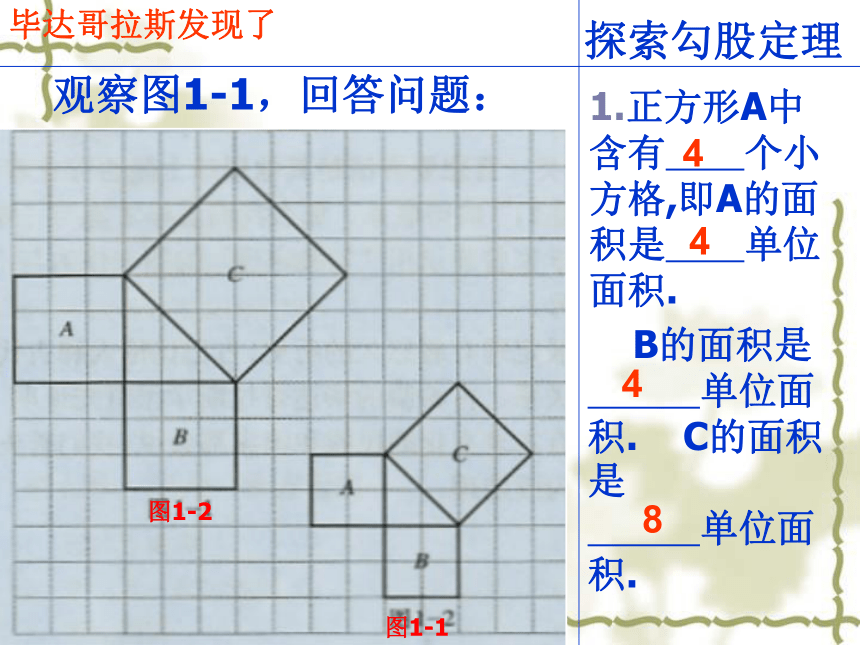
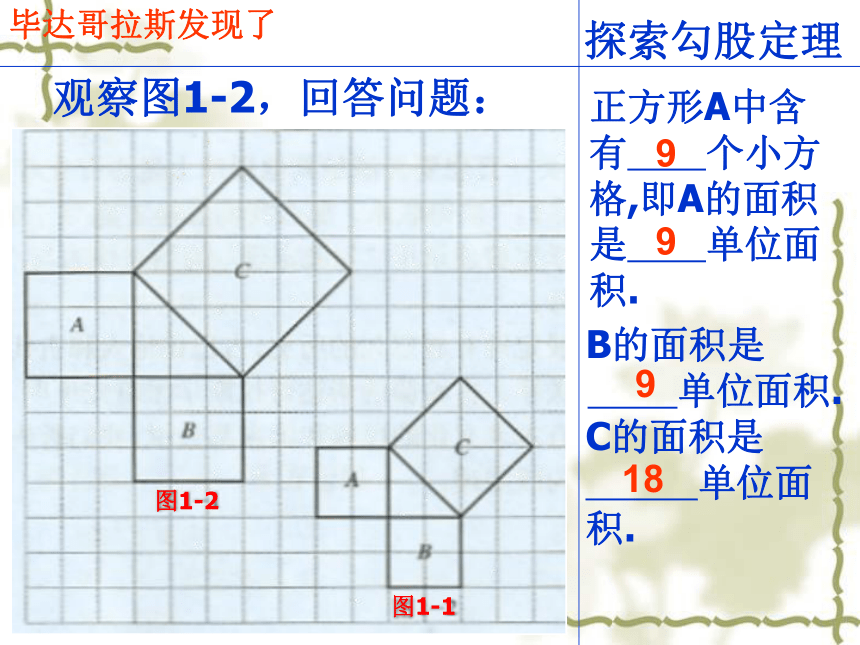
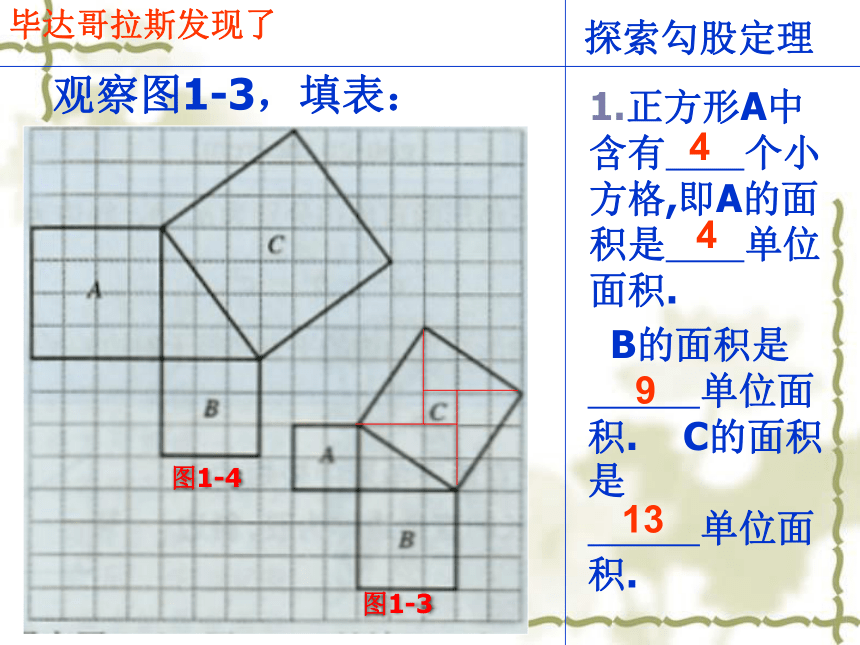
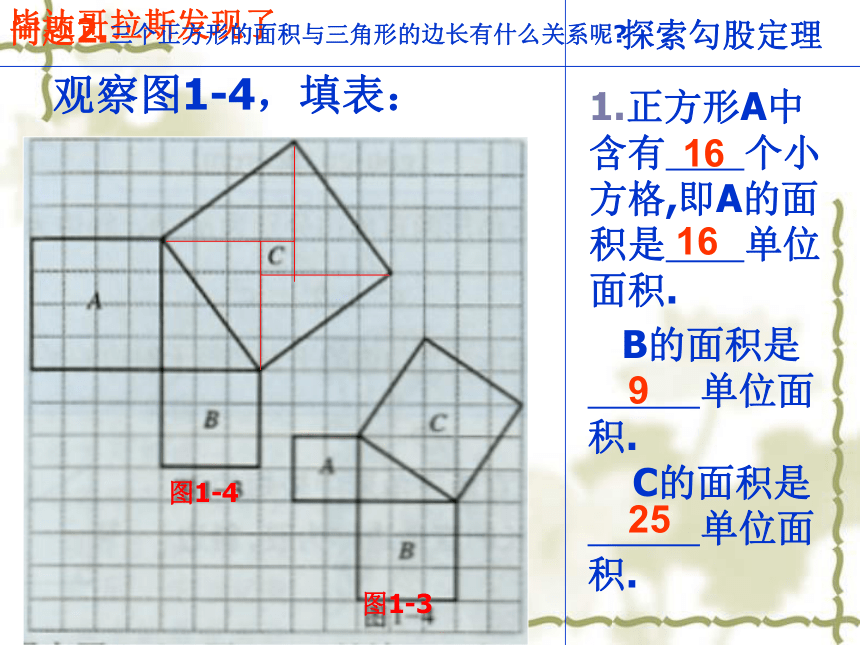
5.证明两个直角三角形全等有“HL” 活动一:温故而知新h本节课我们再来探索直角三角形新的知识 毕达哥拉斯是古希腊著名的哲学家、数学家、天文学家,相传2500年前,一次,毕达哥拉斯去朋友家作客.在宴席上,其他的宾客都在尽情欢乐,高谈阔论,只有毕达哥拉斯却看着朋友家的方砖地而发起呆来.原来,朋友家的地是用一块块直角三角形形状的砖铺成的,黑白相间,非常美观大方.主人看到毕达哥拉斯的样子非常奇怪,就想过去问他.谁知毕达哥拉斯突破恍然大悟的样子,站起来,大笑着跑回家去了. 同学们,你想知道大哲学家发现了什么吗?活动二 听故事 问题1:大正方形的面积与两个小正方形的面积有什么关系?大正方形的面积=两个小正方形的面积的和探索勾股定理观察图1-1,回答问题:1.正方形A中含有 个小方格,即A的面积是 单位面积. B的面积是 单位面积. C的面积是 单位面积.图1-2图1-14448毕达哥拉斯发现了探索勾股定理观察图1-2,回答问题:正方形A中含有 个小方格,即A的面积是 单位面积.B的面积是 单位面积. C的面积是 单位面积.图1-2图1-1毕达哥拉斯发现了99189探索勾股定理观察图1-3,填表:1.正方形A中含有 个小方格,即A的面积是 单位面积. B的面积是 单位面积. C的面积是 单位面积.图1-4图1-344913毕达哥拉斯发现了探索勾股定理观察图1-4,填表:1.正方形A中含有 个小方格,即A的面积是 单位面积. B的面积是 单位面积. C的面积是 单位面积.图1-4图1-31616925毕达哥拉斯发现了问题2.三个正方形的面积与三角形的边长有什么关系呢?活动三:猜想命题如果直角三角形的两直角边长分别为a,b,斜边长为c,那么 直角三角形三边之间的数量关系?勾股定理——千古第一定理外国人把结论叫毕达哥拉斯 定理我国叫 勾股定理 在约公元前1100年,我国古算书《周髀bì算经》记载,人们已经知道,如果勾是三,股是四,那么弦是五.在我国古代,人们将直角三角形中的
短的直角边叫做勾,
长的直角边叫做股,
斜边叫做弦.
活动四:了解中国历史(你知道吗?) 勾股弦 赵爽指出:按弦图,又可以勾股相乘为朱实二,倍之为朱实四,以勾股之差自相乘为中黄实。加差实,亦成弦实。赵爽弦图朱实朱实朱实C朱实结论:思考:大正方形面积怎么求?思考:大正方形面积怎么求? 勾股定理:如果直角三角形两直角边分别 为a、b,斜边为c,那么即 直角三角形两直角边 的平方和等于斜边的平方。证明结论得到定理经过证明被确认正确的命题叫做定理.活动五:亲身体念按图已知直角三角形两直角边a,b量出斜边c填表2525510100100131691691、勾股定理是几何中最重要的定理之一,
它揭示了直角三角形三边之间的数量关系.
2、勾股定理的主要作用是 在直角三角形中,
已知任意两边求第三边的长。结论:S1+S2+S3+S4=S5+S6=S7活动六:活学活用美丽的勾股树⑴已知: a=3, b=4,求c⑵已知: c =10,a=6,求b活动六:活学活用1、已知, Rt△ABC 中,a,b为的两条直角边,c为斜边,求:b探究一个门框尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?活动六:活学活用1、已知:△ABC,AB=AC=17,BC=16,则高AD=_,S△ABC=_. 2、池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m。你能求出A、B两点间的距离吗?(结果保留整数)拓展延伸命题1 如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.勾股定理x课堂小结2、 勾股定理是几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系.⒊勾股定理的主要作用是 在直角三角形中,已知任意两边求第三边的长。
2.两锐角互余∠A+∠B=90°
3.三角形的面积s=1/2ab=1/2hc
4. 30°所对的直角边等于斜边的一半
5.证明两个直角三角形全等有“HL” 活动一:温故而知新h本节课我们再来探索直角三角形新的知识 毕达哥拉斯是古希腊著名的哲学家、数学家、天文学家,相传2500年前,一次,毕达哥拉斯去朋友家作客.在宴席上,其他的宾客都在尽情欢乐,高谈阔论,只有毕达哥拉斯却看着朋友家的方砖地而发起呆来.原来,朋友家的地是用一块块直角三角形形状的砖铺成的,黑白相间,非常美观大方.主人看到毕达哥拉斯的样子非常奇怪,就想过去问他.谁知毕达哥拉斯突破恍然大悟的样子,站起来,大笑着跑回家去了. 同学们,你想知道大哲学家发现了什么吗?活动二 听故事 问题1:大正方形的面积与两个小正方形的面积有什么关系?大正方形的面积=两个小正方形的面积的和探索勾股定理观察图1-1,回答问题:1.正方形A中含有 个小方格,即A的面积是 单位面积. B的面积是 单位面积. C的面积是 单位面积.图1-2图1-14448毕达哥拉斯发现了探索勾股定理观察图1-2,回答问题:正方形A中含有 个小方格,即A的面积是 单位面积.B的面积是 单位面积. C的面积是 单位面积.图1-2图1-1毕达哥拉斯发现了99189探索勾股定理观察图1-3,填表:1.正方形A中含有 个小方格,即A的面积是 单位面积. B的面积是 单位面积. C的面积是 单位面积.图1-4图1-344913毕达哥拉斯发现了探索勾股定理观察图1-4,填表:1.正方形A中含有 个小方格,即A的面积是 单位面积. B的面积是 单位面积. C的面积是 单位面积.图1-4图1-31616925毕达哥拉斯发现了问题2.三个正方形的面积与三角形的边长有什么关系呢?活动三:猜想命题如果直角三角形的两直角边长分别为a,b,斜边长为c,那么 直角三角形三边之间的数量关系?勾股定理——千古第一定理外国人把结论叫毕达哥拉斯 定理我国叫 勾股定理 在约公元前1100年,我国古算书《周髀bì算经》记载,人们已经知道,如果勾是三,股是四,那么弦是五.在我国古代,人们将直角三角形中的
短的直角边叫做勾,
长的直角边叫做股,
斜边叫做弦.
活动四:了解中国历史(你知道吗?) 勾股弦 赵爽指出:按弦图,又可以勾股相乘为朱实二,倍之为朱实四,以勾股之差自相乘为中黄实。加差实,亦成弦实。赵爽弦图朱实朱实朱实C朱实结论:思考:大正方形面积怎么求?思考:大正方形面积怎么求? 勾股定理:如果直角三角形两直角边分别 为a、b,斜边为c,那么即 直角三角形两直角边 的平方和等于斜边的平方。证明结论得到定理经过证明被确认正确的命题叫做定理.活动五:亲身体念按图已知直角三角形两直角边a,b量出斜边c填表2525510100100131691691、勾股定理是几何中最重要的定理之一,
它揭示了直角三角形三边之间的数量关系.
2、勾股定理的主要作用是 在直角三角形中,
已知任意两边求第三边的长。结论:S1+S2+S3+S4=S5+S6=S7活动六:活学活用美丽的勾股树⑴已知: a=3, b=4,求c⑵已知: c =10,a=6,求b活动六:活学活用1、已知, Rt△ABC 中,a,b为的两条直角边,c为斜边,求:b探究一个门框尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?活动六:活学活用1、已知:△ABC,AB=AC=17,BC=16,则高AD=_,S△ABC=_. 2、池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m。你能求出A、B两点间的距离吗?(结果保留整数)拓展延伸命题1 如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.勾股定理x课堂小结2、 勾股定理是几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系.⒊勾股定理的主要作用是 在直角三角形中,已知任意两边求第三边的长。
