22.1二次函数的图象和性质 二次函数中的符号问题复习课件
文档属性
| 名称 | 22.1二次函数的图象和性质 二次函数中的符号问题复习课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 439.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-26 00:00:00 | ||
图片预览







文档简介
课件20张PPT。二次函数中的符号问题二次函数复习(3)本课的学习目标:
1、关于二次函数复习(1)中的
易错题回顾;
2、二次函数中的符号问题学习。一、易错题回顾大家来找茬1、(二次函数概念)下列函数中是二次
函数的是_______________①、④、⑤、①、 ②、
③、 ④、
⑤、 ⑥、2、若 是二次函数,
则m=______2或03、(开口、顶点、对称轴)
①抛物线 的开口向下,
对称轴是直线x=3,顶点坐标(3,0).
②抛物线 的开口向上,
对称轴是直线x=3,顶点坐标是(3,0).
③抛物线 的顶点坐标
是(-8,0).
大家来找茬大家来找茬4、(平移问题)
抛物线 可以看作由抛物线
向下平移7个单位得到。
5、(增减性)
已知二次函数的图像上有三点 A 、
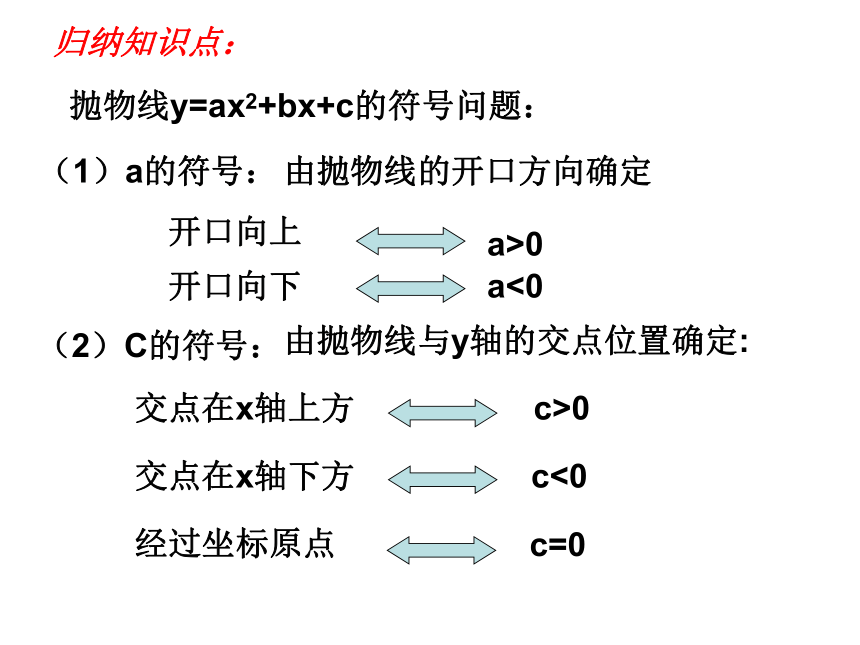
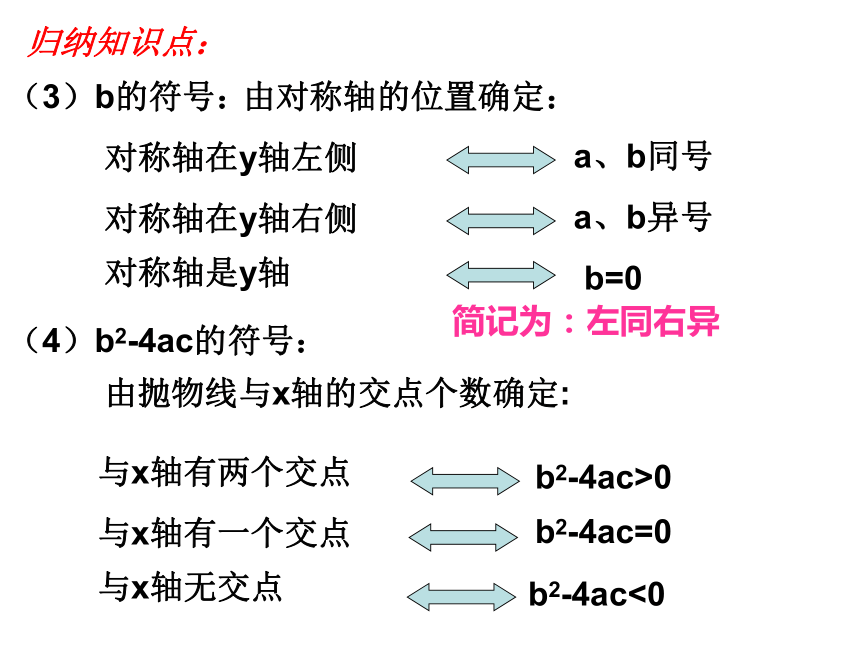
B(5, )、C(- , )则二次函数中的符号问题(a、b、c、△等符号)回味知识点:1、抛物线y=ax2+bx+c的开口方向与什么有关?2、抛物线y=ax2+bx+c与y轴的交点是 .3、抛物线y=ax2+bx+c的对称轴是 .归纳知识点:抛物线y=ax2+bx+c的符号问题:(1)a的符号:由抛物线的开口方向确定开口向上a>0开口向下a<0(2)C的符号:由抛物线与y轴的交点位置确定:交点在x轴上方c>0交点在x轴下方c<0经过坐标原点c=0(3)b的符号:由对称轴的位置确定:对称轴在y轴左侧a、b同号对称轴在y轴右侧a、b异号对称轴是y轴b=0(4)b2-4ac的符号:由抛物线与x轴的交点个数确定:与x轴有两个交点b2-4ac>0与x轴有一个交点b2-4ac=0与x轴无交点b2-4ac<0归纳知识点:简记为:左同右异归纳知识点:抛物线y=ax2+bx+c的符号问题:(5)a+b+c的符号:由x=1时抛物线上的点的位置确定(6)a-b+c的符号:由x=-1时抛物线上的点的位置确定你还可想到什么?快速回答:抛物线y=ax2+bx+c如图所示,试确定a、b、c、
△的符号:xoy抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:xyo快速回答:抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:xyo快速回答:练一练:1.已知:二次函数y=ax2+bx+c的图象如图所示,则点M( ,a)在( )A、第一象限
B、第二象限
C、第三象限
D、第四象限 xoyD练一练:2、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①b>0;②c<0;③4a+2b+c > 0;④(a+c)2<b2,其中正确的个数是 ( )
A、4个 B、3个
C、2个 D、1个B
6.如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0),且与y轴相交于负半轴.
①a>0;② b>0;③c>0;④ a+b+c=0;
⑤ abc<0;⑥2a+b>0;
⑦a+c=1;⑧a>1.
其中正确结论的
序号是 ___.
例题:①④ ⑥ ⑦ ⑧练一练:3、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①abc>0;②b=2a;③a+b+c<0;④a+b-c>0; ⑤a-b+c>0正确的个数是 ( )
A、2个 B、3个
C、4个 D、5个C这节课你有哪些体会?1.a,b,c等符号与二次函数y=ax2+bx+c有密切的联系;
2.解决这类问题的关键是运用数形结合思想,即会观察图象;如遇到2a+b,2a-b要与对称轴联系等;
3.要注意灵活运用数学知识,具体问题具体分析……作业布置:1、导学单最后一题;
2、预习二次函数实际应用。
1、关于二次函数复习(1)中的
易错题回顾;
2、二次函数中的符号问题学习。一、易错题回顾大家来找茬1、(二次函数概念)下列函数中是二次
函数的是_______________①、④、⑤、①、 ②、
③、 ④、
⑤、 ⑥、2、若 是二次函数,
则m=______2或03、(开口、顶点、对称轴)
①抛物线 的开口向下,
对称轴是直线x=3,顶点坐标(3,0).
②抛物线 的开口向上,
对称轴是直线x=3,顶点坐标是(3,0).
③抛物线 的顶点坐标
是(-8,0).
大家来找茬大家来找茬4、(平移问题)
抛物线 可以看作由抛物线
向下平移7个单位得到。
5、(增减性)
已知二次函数的图像上有三点 A 、
B(5, )、C(- , )则二次函数中的符号问题(a、b、c、△等符号)回味知识点:1、抛物线y=ax2+bx+c的开口方向与什么有关?2、抛物线y=ax2+bx+c与y轴的交点是 .3、抛物线y=ax2+bx+c的对称轴是 .归纳知识点:抛物线y=ax2+bx+c的符号问题:(1)a的符号:由抛物线的开口方向确定开口向上a>0开口向下a<0(2)C的符号:由抛物线与y轴的交点位置确定:交点在x轴上方c>0交点在x轴下方c<0经过坐标原点c=0(3)b的符号:由对称轴的位置确定:对称轴在y轴左侧a、b同号对称轴在y轴右侧a、b异号对称轴是y轴b=0(4)b2-4ac的符号:由抛物线与x轴的交点个数确定:与x轴有两个交点b2-4ac>0与x轴有一个交点b2-4ac=0与x轴无交点b2-4ac<0归纳知识点:简记为:左同右异归纳知识点:抛物线y=ax2+bx+c的符号问题:(5)a+b+c的符号:由x=1时抛物线上的点的位置确定(6)a-b+c的符号:由x=-1时抛物线上的点的位置确定你还可想到什么?快速回答:抛物线y=ax2+bx+c如图所示,试确定a、b、c、
△的符号:xoy抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:xyo快速回答:抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:xyo快速回答:练一练:1.已知:二次函数y=ax2+bx+c的图象如图所示,则点M( ,a)在( )A、第一象限
B、第二象限
C、第三象限
D、第四象限 xoyD练一练:2、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①b>0;②c<0;③4a+2b+c > 0;④(a+c)2<b2,其中正确的个数是 ( )
A、4个 B、3个
C、2个 D、1个B
6.如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0),且与y轴相交于负半轴.
①a>0;② b>0;③c>0;④ a+b+c=0;
⑤ abc<0;⑥2a+b>0;
⑦a+c=1;⑧a>1.
其中正确结论的
序号是 ___.
例题:①④ ⑥ ⑦ ⑧练一练:3、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①abc>0;②b=2a;③a+b+c<0;④a+b-c>0; ⑤a-b+c>0正确的个数是 ( )
A、2个 B、3个
C、4个 D、5个C这节课你有哪些体会?1.a,b,c等符号与二次函数y=ax2+bx+c有密切的联系;
2.解决这类问题的关键是运用数形结合思想,即会观察图象;如遇到2a+b,2a-b要与对称轴联系等;
3.要注意灵活运用数学知识,具体问题具体分析……作业布置:1、导学单最后一题;
2、预习二次函数实际应用。
同课章节目录
