人教版高中数学必修一1.3.3《函数单调性的概念 》获奖课件(40张)
文档属性
| 名称 | 人教版高中数学必修一1.3.3《函数单调性的概念 》获奖课件(40张) |  | |
| 格式 | zip | ||
| 文件大小 | 922.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-26 10:37:52 | ||
图片预览



文档简介
课件40张PPT。1.3.1 单调性与最大(小)值 第1课时 函数单调性的概念数与形 本是相倚依 焉能分作两边飞 数无形时少直觉 形少数时难入微 数形结合百般好 隔离分家万事休 切莫忘 几何代数统一体 永远联系莫分离
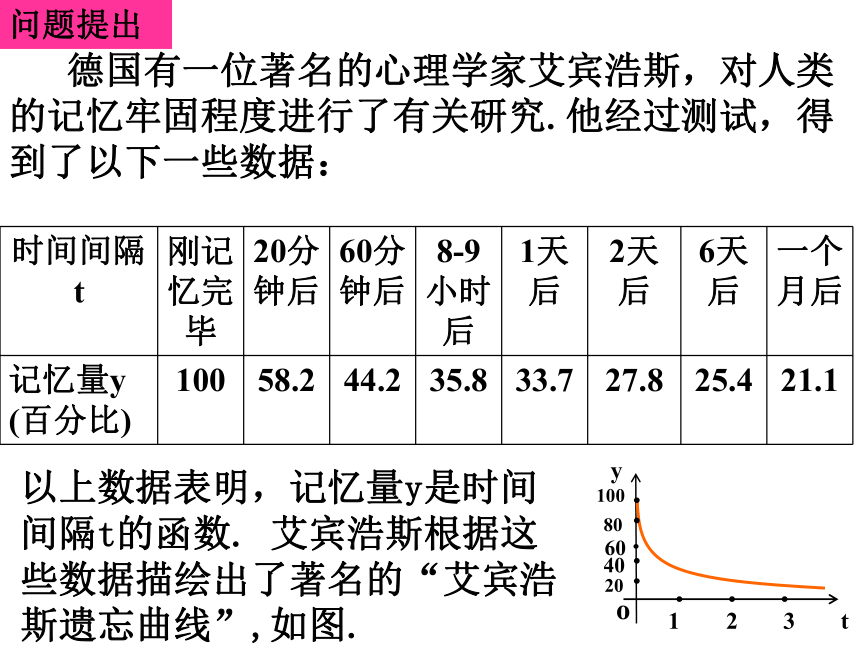
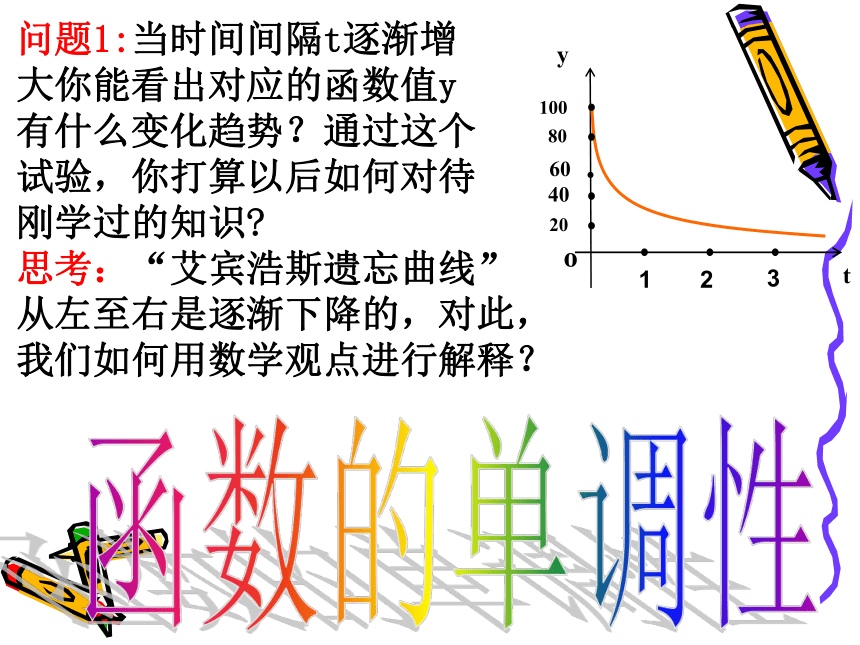
——— 华罗庚问题提出 德国有一位著名的心理学家艾宾浩斯,对人类的记忆牢固程度进行了有关研究.他经过测试,得到了以下一些数据:函数的单调性问题1:当时间间隔t逐渐增 大你能看出对应的函数值y
有什么变化趋势?通过这个
试验,你打算以后如何对待
刚学过的知识?
思考:“艾宾浩斯遗忘曲线”
从左至右是逐渐下降的,对此,
我们如何用数学观点进行解释?学习目标1、理解函数单调性的概念
2、掌握判断一些简单函数的
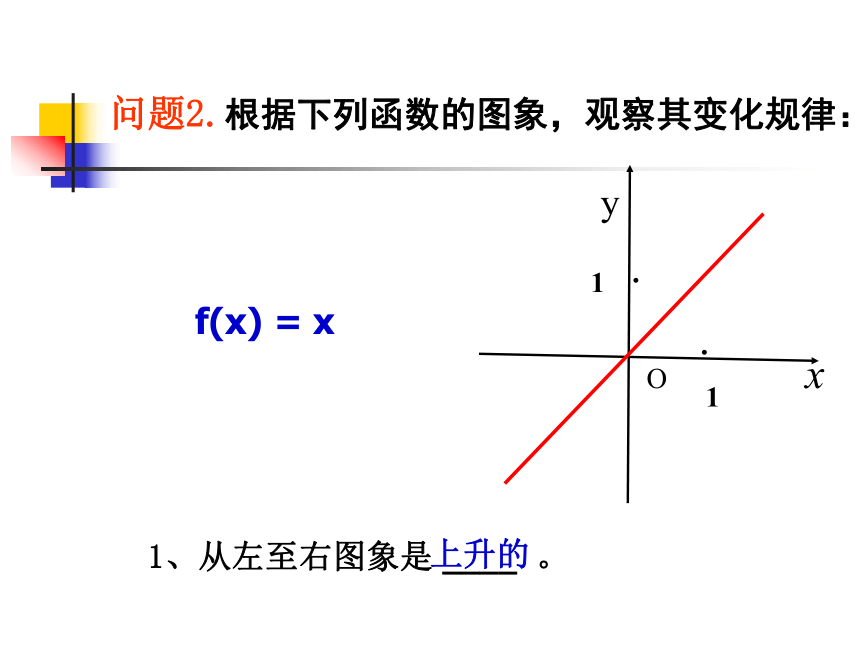
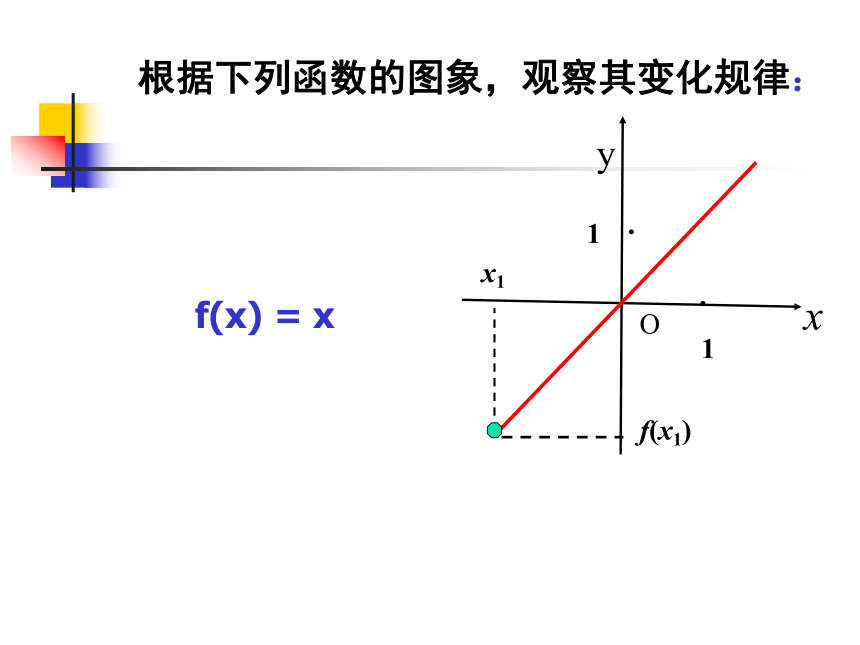
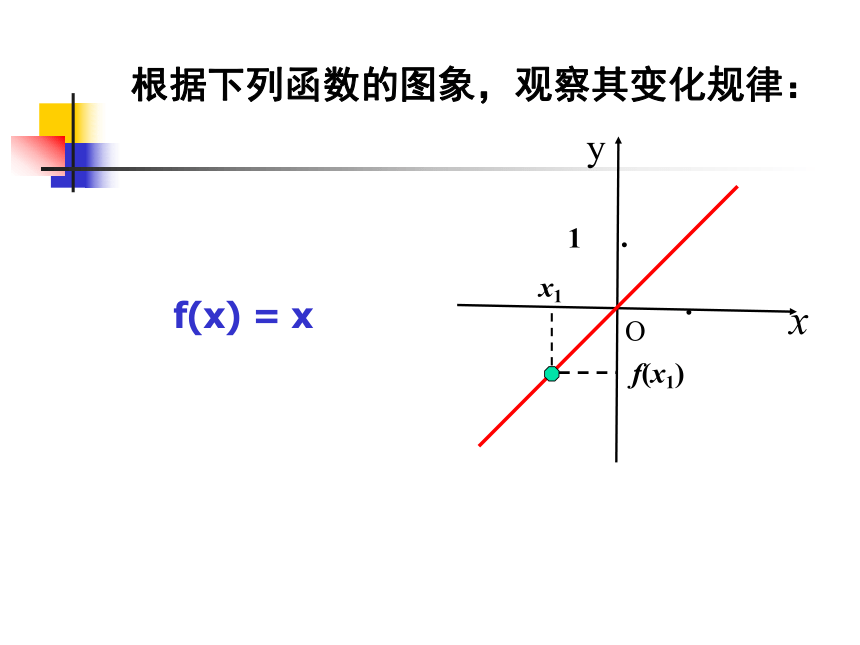
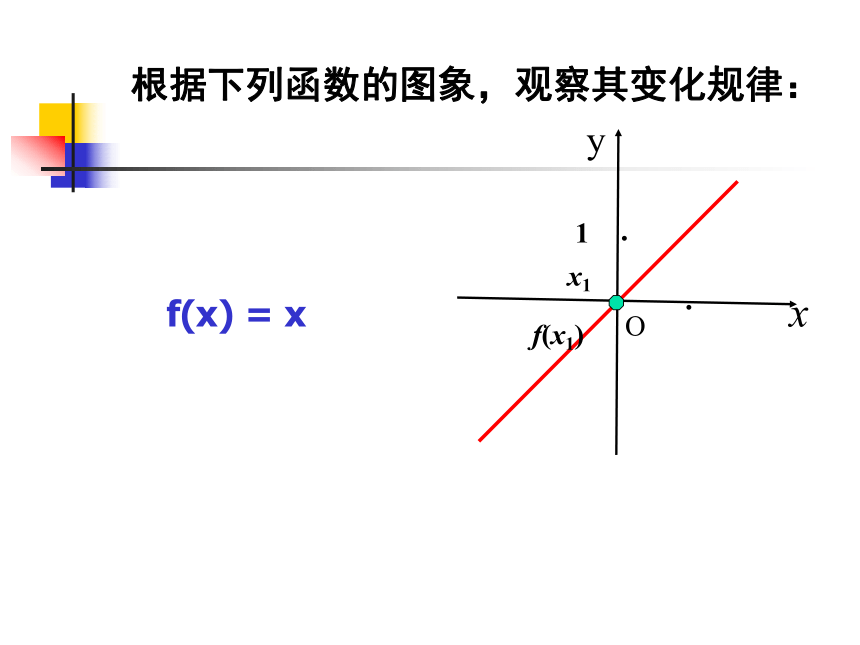
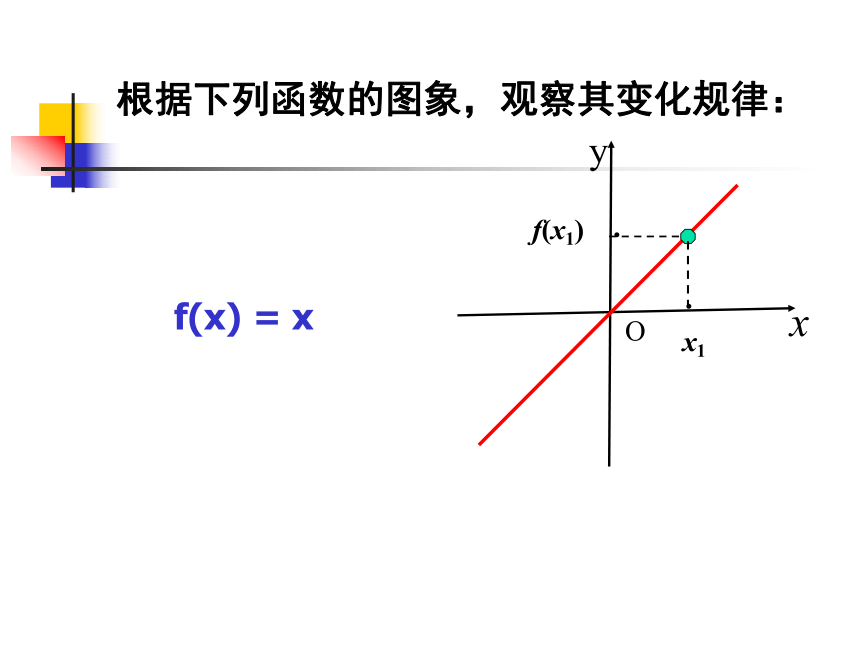
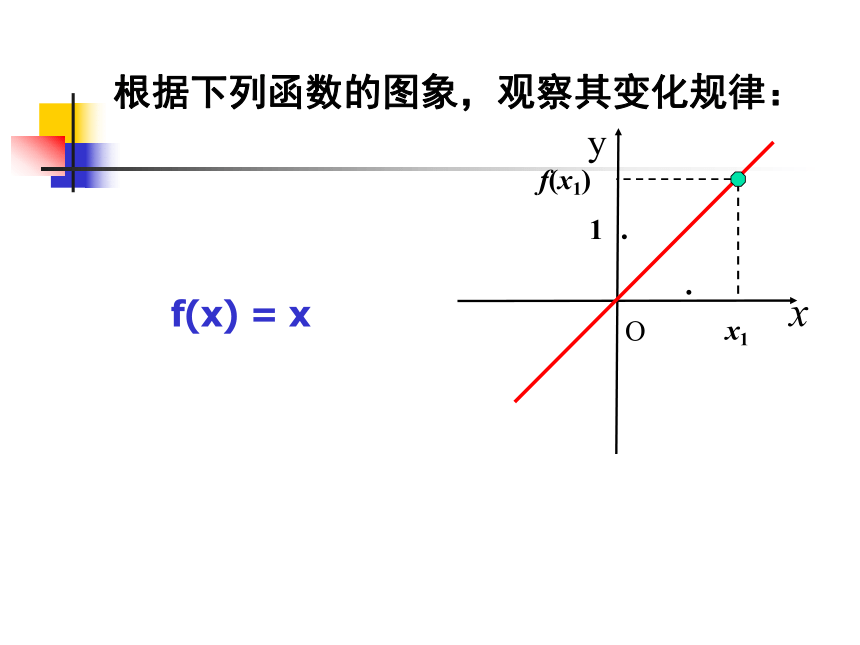
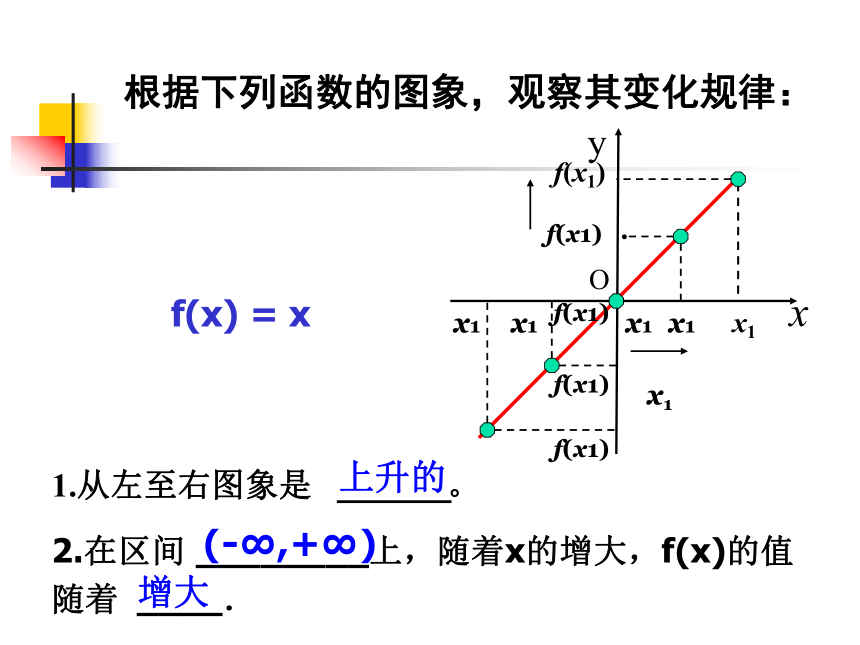
单调性的方法 问题2.根据下列函数的图象,观察其变化规律: 1、从左至右图象是 ____ 。f(x) = x 上升的 x1f(x1)x1根据下列函数的图象,观察其变化规律: f(x) = xxyO1··f(x1)根据下列函数的图象,观察其变化规律: f(x) = xxyO1··x1f(x1)根据下列函数的图象,观察其变化规律: f(x) = xxyO··x1f(x1)(-∞,+∞)增大上升的根据下列函数的图象,观察其变化规律: f(x) = xxyO·x1f(x1)x1x1x1x1x1f(x1)f(x1)f(x1)f(x1)1.从左至右图象是 。
2.在区间 ________上,随着x的增大,f(x)的值随着 ____. f(x) = x2问题3.根据下列函数的图象,观察其变化规律: 图象在y轴左侧“下降”图象在y轴右侧“上升” f(x) = x2根据下列函数的图象,观察其变化规律: Oxy·1·1x1f(x1)f(x) = x2根据下列函数的图象,观察其变化规律: Oxy1·1·f(x1)x1f(x) = x2根据下列函数的图象,观察其变化规律: Ox1·1f(x1)x1 f(x) = x2根据下列函数的图象,观察其变化规律: Oxyf(x1)x1f(x) = x2根据下列函数的图象,观察其变化规律: Oxyf(x1)x11、在区间 ____ 上,f(x)的值随着x的增大而 ______.
f(x) = x2(-∞,0]减小画出下列函数的图象,观察其变化规律: Oxyf(x1)x1f(x1)f(x1)x1x1
2、 在区间 _____ 上,f(x)的值随着x的增大而 _____. f(x) = x2(0,+∞)增大根据下列函数的图象,观察其变化规律: Oxyf(x1)x1x1x1f(x1)f(x1)1、在区间 ____ 上,f(x)的值随着x的增大而 ______.
2、 在区间 _____ 上,f(x)的值随着x的增大而 _____. f(x) = x2(-∞,0](0,+∞)增大减小根据下列函数的图象,观察其变化规律: 图象在y轴左侧”下降“图象在y轴右侧”上升“Oxyf(x1)x1x1x1f(x1)f(x1)x1x1问题4:函数的表示法有三种: 、 、 . 既然由图象可得到函数的增减性,那么用列表法能否得到呢?1.在区间 ____ 上,f(x)的值随着x的增大而 ______.
2.在区间 _____ 上,f(x)的值随着x的增大而 _____. (-∞,0]减小(0,+∞)增大图象法列表法解析法问题5.对于二次函数 , 我们可以这样描述“在区间(0,+∞)上,随着x的增大,相应的f(x)也随着增大”。那么,如何用精确地数量关系来描述这一性质呢?Oxy利用函数解析式对于(0,+∞)上的任意两个x1、x2,当x1f(x2),那么就说f(x)在区间D上是减函数 .2.减函数 1、增(减)函数是相对于定义域I内的某个区
间D(D I) 而言的 ,是函数的局部性质;注意: 2 、 x1,x2必须是区间D内任意两个自变量的
取值,而不是某些特殊值。
3、当x1 f(x1)>f(x2) 则f(x)是增函数或减函数. 如果函数y=f(x)在某个区间D上是增函数或减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间. 3.函数的单调性定义
0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····从左到右,图像上升y随x的增大而增大从左到右,图象下降y随x增大而减小当x1<x2时, f(x1) < f(x2)
当x1<x2时, f(x1) > f(x2)
例1.下图是定义在区间[-5,5]上的函数y=f(x),根据图象说出函数的单调区间,以及在每个区间上,它是增函数还是减函数?解:函数y=f(x)的单调区间有 [-5,-2),[-2,1),[1,3),[3,5] 其中y=f(x)在区间[-5,-2), [1,3)是减函数,
在区间[-2,1), [3,5] 上是增函数。
(1)函数是增函数,还是减函数,是对函数
定义域内的某个 来说的.
(2)在单调区间上的增函数的图象 是
上升的,减函数的图象是下降的.
(3)如果函数在某个区间上又有增,又有减,
那么这个函数在这个区间上不具有 .归纳总结:区间从左至右单调性思考?思考:画出反比例函数 的图象.
1、这个函数的定义域是什么?
2、它在定义域I上的单调性怎样?
3、函数 在 上是否具有单调性?(-∞,0) ∪(0,+∞) 在区间(-∞,0) 和(0,+∞)上都是单调递减。解:定义域为在(-∞,+∞)是增函数K>0
在(-∞,0)和(0,+∞)是减函数K<0
在(-∞,0)和(0,+∞)是增函数K>0在(∞,+∞)是减函数
课堂小结 2.函数的单调性的判断:
①数值列表法;(不常用)
②图象法;
③定义法
函数的单调性一般是先根据图象判断,
再利用定义证明.本节你学到了什么知识?1.函数单调性的定义1.根据图象说出函数的的单调区间,以及在
每一单调区间上,函数是增函数还是减函数.当堂检测2、下列结论正确的是( )A.函数y=kx(k为常数,k<0)在R上是增函数。
B.函数y=x2在R上是增函数。
C. 在定义域内为减函数。
D. 在 上为减函数。
D3、函数 的减区间是( )D4、设f(x)是R上的减函数,
若
则实数m的取值范围是
.
5、设函数f(x)=(2a-1)x+b是R 上的减函数,则( )D6、函数 的单调区间解:课本P39 习题1.3
A组第1题 .五、作业
——— 华罗庚问题提出 德国有一位著名的心理学家艾宾浩斯,对人类的记忆牢固程度进行了有关研究.他经过测试,得到了以下一些数据:函数的单调性问题1:当时间间隔t逐渐增 大你能看出对应的函数值y
有什么变化趋势?通过这个
试验,你打算以后如何对待
刚学过的知识?
思考:“艾宾浩斯遗忘曲线”
从左至右是逐渐下降的,对此,
我们如何用数学观点进行解释?学习目标1、理解函数单调性的概念
2、掌握判断一些简单函数的
单调性的方法 问题2.根据下列函数的图象,观察其变化规律: 1、从左至右图象是 ____ 。f(x) = x 上升的 x1f(x1)x1根据下列函数的图象,观察其变化规律: f(x) = xxyO1··f(x1)根据下列函数的图象,观察其变化规律: f(x) = xxyO1··x1f(x1)根据下列函数的图象,观察其变化规律: f(x) = xxyO··x1f(x1)(-∞,+∞)增大上升的根据下列函数的图象,观察其变化规律: f(x) = xxyO·x1f(x1)x1x1x1x1x1f(x1)f(x1)f(x1)f(x1)1.从左至右图象是 。
2.在区间 ________上,随着x的增大,f(x)的值随着 ____. f(x) = x2问题3.根据下列函数的图象,观察其变化规律: 图象在y轴左侧“下降”图象在y轴右侧“上升” f(x) = x2根据下列函数的图象,观察其变化规律: Oxy·1·1x1f(x1)f(x) = x2根据下列函数的图象,观察其变化规律: Oxy1·1·f(x1)x1f(x) = x2根据下列函数的图象,观察其变化规律: Ox1·1f(x1)x1 f(x) = x2根据下列函数的图象,观察其变化规律: Oxyf(x1)x1f(x) = x2根据下列函数的图象,观察其变化规律: Oxyf(x1)x11、在区间 ____ 上,f(x)的值随着x的增大而 ______.
f(x) = x2(-∞,0]减小画出下列函数的图象,观察其变化规律: Oxyf(x1)x1f(x1)f(x1)x1x1
2、 在区间 _____ 上,f(x)的值随着x的增大而 _____. f(x) = x2(0,+∞)增大根据下列函数的图象,观察其变化规律: Oxyf(x1)x1x1x1f(x1)f(x1)1、在区间 ____ 上,f(x)的值随着x的增大而 ______.
2、 在区间 _____ 上,f(x)的值随着x的增大而 _____. f(x) = x2(-∞,0](0,+∞)增大减小根据下列函数的图象,观察其变化规律: 图象在y轴左侧”下降“图象在y轴右侧”上升“Oxyf(x1)x1x1x1f(x1)f(x1)x1x1问题4:函数的表示法有三种: 、 、 . 既然由图象可得到函数的增减性,那么用列表法能否得到呢?1.在区间 ____ 上,f(x)的值随着x的增大而 ______.
2.在区间 _____ 上,f(x)的值随着x的增大而 _____. (-∞,0]减小(0,+∞)增大图象法列表法解析法问题5.对于二次函数 , 我们可以这样描述“在区间(0,+∞)上,随着x的增大,相应的f(x)也随着增大”。那么,如何用精确地数量关系来描述这一性质呢?Oxy利用函数解析式对于(0,+∞)上的任意两个x1、x2,当x1
间D(D I) 而言的 ,是函数的局部性质;注意: 2 、 x1,x2必须是区间D内任意两个自变量的
取值,而不是某些特殊值。
3、当x1
0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····从左到右,图像上升y随x的增大而增大从左到右,图象下降y随x增大而减小当x1<x2时, f(x1) < f(x2)
当x1<x2时, f(x1) > f(x2)
例1.下图是定义在区间[-5,5]上的函数y=f(x),根据图象说出函数的单调区间,以及在每个区间上,它是增函数还是减函数?解:函数y=f(x)的单调区间有 [-5,-2),[-2,1),[1,3),[3,5] 其中y=f(x)在区间[-5,-2), [1,3)是减函数,
在区间[-2,1), [3,5] 上是增函数。
(1)函数是增函数,还是减函数,是对函数
定义域内的某个 来说的.
(2)在单调区间上的增函数的图象 是
上升的,减函数的图象是下降的.
(3)如果函数在某个区间上又有增,又有减,
那么这个函数在这个区间上不具有 .归纳总结:区间从左至右单调性思考?思考:画出反比例函数 的图象.
1、这个函数的定义域是什么?
2、它在定义域I上的单调性怎样?
3、函数 在 上是否具有单调性?(-∞,0) ∪(0,+∞) 在区间(-∞,0) 和(0,+∞)上都是单调递减。解:定义域为在(-∞,+∞)是增函数K>0
在(-∞,0)和(0,+∞)是减函数K<0
在(-∞,0)和(0,+∞)是增函数K>0在(∞,+∞)是减函数
课堂小结 2.函数的单调性的判断:
①数值列表法;(不常用)
②图象法;
③定义法
函数的单调性一般是先根据图象判断,
再利用定义证明.本节你学到了什么知识?1.函数单调性的定义1.根据图象说出函数的的单调区间,以及在
每一单调区间上,函数是增函数还是减函数.当堂检测2、下列结论正确的是( )A.函数y=kx(k为常数,k<0)在R上是增函数。
B.函数y=x2在R上是增函数。
C. 在定义域内为减函数。
D. 在 上为减函数。
D3、函数 的减区间是( )D4、设f(x)是R上的减函数,
若
则实数m的取值范围是
.
5、设函数f(x)=(2a-1)x+b是R 上的减函数,则( )D6、函数 的单调区间解:课本P39 习题1.3
A组第1题 .五、作业
