2.7正方形练习题

21世纪教育网 –中小学教育资源及组卷应用平台
2.7正方形练习题
一、选择题
1、正方形具有而菱形不一定具有的性质是( )
A.内角和为360° B.对角线相等
C.对角线平分内角 D.对角线互相垂直平分
2、四边形ABCD中，AC、BD相交于O，下列条件中，能判定这个四边形是正方形的是（ ）
A. AO = BO = CO = DO，AC⊥BD B. AB∥CD，AC = BD
C. AD∥BC，∠A =∠C D. AO = CO，BO = CO，AB = BC
3、四边形ABCD的对角线AC = BD，且AC⊥BD，分别过A、B、C、D作对角线的平行线，则所构成的四边形是（ ）21世纪教育网版权所有
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
4、如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为　(　　)
A.14　　 B.15 C.16　　　 D.17
5、已知四边形ABCD,对角线AC与BD互相垂直.顺次连接其四条边的中点,得到新四边形的形状一定是　(　　) 21cnjy.com
A.梯形　　　 B.矩形　　　 C.菱形　　 　D.正方形
6. 一个正方形和一个等腰三角形有相同的周长，等腰三角形的边长分别为5.6cm和13.2cm，则这个正方形的面积为( )21·cn·jy·com
A.24 B.36 C.48 D.64
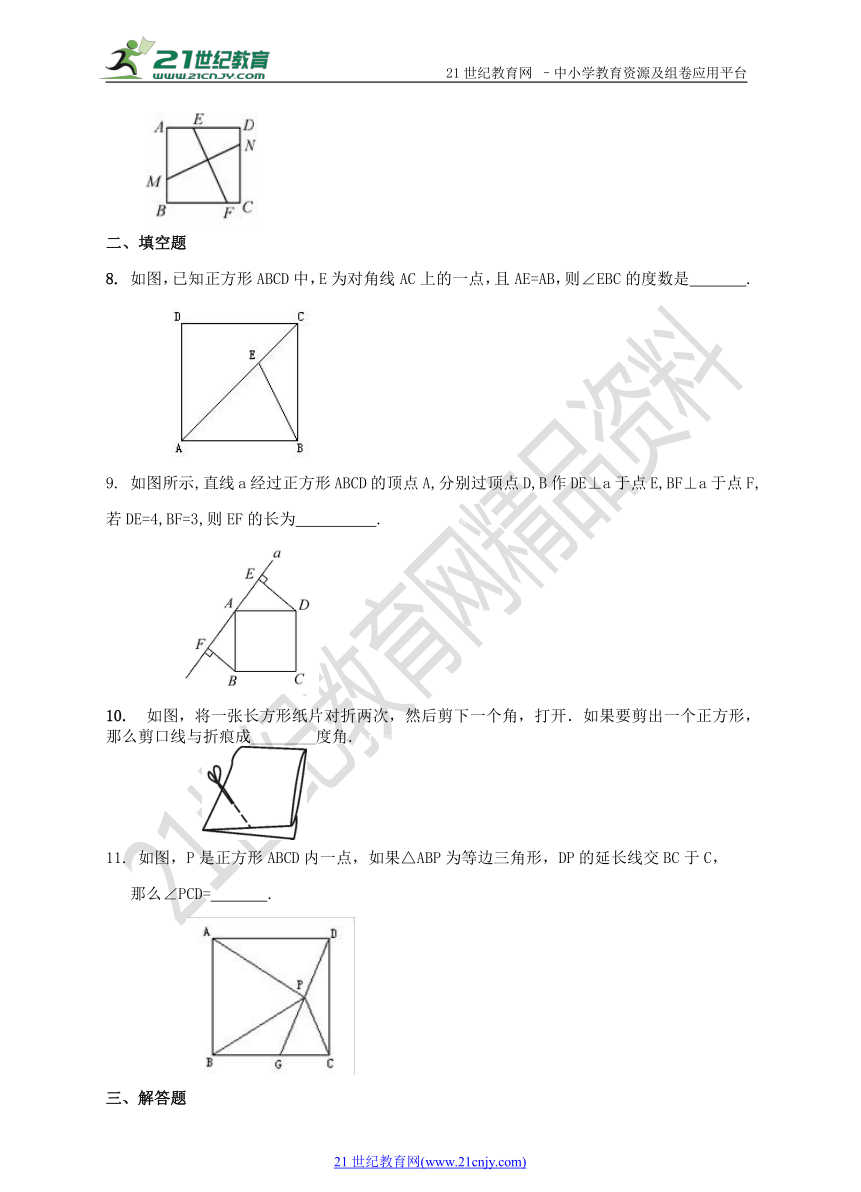
7. 如图，正方形ABCD内有两条相交线段MN、EF，M、N、E、F分别在边AB、CD、AD、BC上．小明认为：若MN=EF，则MN⊥EF；小亮认为: 若MN⊥EF，则MN=EF．你认为（ ）
A．仅小明对 B．仅小亮对 C．两人都对 D．两人都不对
二、填空题
8. 如图，已知正方形ABCD中，E为对角线AC上的一点，且AE=AB，则∠EBC的度数是 .
9. 如图所示,直线a经过正方形ABCD的顶点A,分别过顶点D,B作DE⊥a于点E,BF⊥a于点F,若DE=4,BF=3,则EF的长为　　　　　. www.21-cn-jy.com
10. 如图，将一张长方形纸片对折两次，然后剪下一个角，打开．如果要剪出一个正方形，那么剪口线与折痕成________度角. 【来源：21·世纪·教育·网】
11. 如图，P是正方形ABCD内一点，如果△ABP为等边三角形，DP的延长线交BC于C，
那么∠PCD= .
三、解答题
12.如图，正方形ABCD的边长为6，菱形EFGH的三个顶点E，G，H分别在正方形ABCD的边AB，CD，DA上，且AH＝2，连接CF.若DG＝2，求证：菱形EFGH为正方形．
13. 如图，正方形CEFG的边GC在正方形ABCD的边CD上，延长CD到H，使DH＝CE，K在BC边上，且BK＝CE，求证：四边形AKFH为正方形．21教育网
14．如图,点O是线段AB上的一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F 2·1·c·n·j·y
(1)求证:四边形CDOF是矩形.
(2)当∠AOC为多少度时,四边形CDOF是正方形 并说明理由.
15. 已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,连接AE,交边BC于点G. 21·世纪*教育网
(1)求证:四边形ABGD是平行四边形.
(2)如果AD=AB,求证:四边形DGEC是正方形.
答案：
1、B. 2、A. 3、D. 4、B. 5. B 6. D 7.Cwww-2-1-cnjy-com
8. 22.5°
10. 45
11. 15°
12.
证明：∵四边形ABCD是正方形，∴∠D＝∠A＝90°.
∵四边形EFGH是菱形，∴HG＝HE.∵DG＝AH＝2，
∴Rt△HDG≌Rt△EAH，∴∠DHG＝∠AEH.
又∵∠AEH＋∠AHE＝90°，
∴∠DHG＋∠AHE＝90°，∴∠GHE＝90°，
∴菱形EFGH为正方形．　
13. 证明：∵四边形ABCD和四边形CEFG是正方形，
∴AB＝BC＝CD＝AD，∠BAD＝∠DCB＝∠B＝∠ADC＝90°，∠GCE＝∠E＝∠GFE＝∠CGF＝90°，
∴∠ADH＝∠HGF＝∠E＝∠B＝90°.
又∵DH＝CE，BK＝CE，
∴BK＝GF＝DH＝EF，KE＝GH＝AB＝AD，
∴△ABK≌△KEF≌△HGF≌△ADH，
∴AK＝KF＝HF＝AH，∠BAK＝∠DAH.
∵∠BAD＝90°，∴∠HAK＝∠HAD＋∠DAK＝∠BAK＋∠DAK＝∠BAD＝90°，
∴四边形AKFH为正方形．
14.
(1)∵OD平分∠AOC,OF平分∠COB,
∴∠AOC=2∠COD,∠COB=2∠COF,
∵∠AOC+∠BOC=180°,
∴2∠COD+2∠COF=180°,
∴∠COD+∠COF=90°,∴∠DOF=90°.
∵OA=OC,OD平分∠AOC,
∴OD⊥AC,AD=DC(等腰三角形的“三线合一”的性质),
∴∠CDO=90°,
∵CF⊥OF,∴∠CFO=90°,
∴四边形CDOF是矩形.
(2)当∠AOC=90°时,四边形CDOF是正方形.
理由如下:∵∠AOC=90°,AD=DC,
∴OD=DC.
又由(1)知四边形CDOF是矩形,则
四边形CDOF是正方形.
因此,当∠AOC=90°时,四边形CDOF是正方形.
15.
(1)如图,连接AC,BE.
∵DE⊥BC,且F是DE的中点,∴DC=EC,
即得∠DCF=∠ECF,
又∵AD∥BC,AB=CD,∴∠ABC=∠DCF,AB=EC,
∴∠ABC=∠ECF,∴AB∥EC,
∴四边形ABEC是平行四边形,
∴BG=CG=BC,
∵BC=2AD,∴AD=BG,
又∵AD∥BG,∴四边形ABGD是平行四边形.
(2)∵四边形ABGD是平行四边形,
∴AB∥DG,AB=DG,
又∵AB∥EC,AB=EC,∴DG∥EC,DG=EC,
∴四边形DGEC是平行四边形,
又∵DC=EC,∴四边形DGEC是菱形,
∴DG=DC,
由AD=AB,即得CG=DC=DG,
∴DG2+DC2=CG2,∴∠GDC=90°,
∴四边形DGEC是正方形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)