19.2.2 一次函数(3)同步练习
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
19.2.2 一次函数(3)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.设一次函数为y=kx+b,再依条件确定解析式中的未知系数,从而具体写出这个式子的方法叫做待定系数法. 21·cn·jy·com
2.一次函数y=kx+b中有k、b两个待 ( http: / / www.21cnjy.com )定系数,故利用待定系数法时需要根据条件列二元一次方程组(以k和b 为未知数),解方程组就能具体写出一次函数的解析式.
3.用待定系数法求函数解析式的一般步骤:设出含有待定系数的函数解析式;把已知条件(自变量与函数的对应值)代入解析式,得到关于待定系数的方程或方程组;解方程或方程组,求出待定系数; 将求得的待定系数代回所设的解析式.www.21-cn-jy.com
基础知识和能力拓展精练
一、选择题
1.已知直线y=kx+b与y=2x﹣5平行且经过点(1,3),则y=kx+b的表达式是( )
A. y=x+2 B. y=2x+1 C. y=2x+2 D. y=2x+3
2.已知直线与一条经过原点的直线l平行,则这条直线l的函数关系式为( )
A. B. C. D. y=2x
3.已知函数,,的图象交于一点,则值为( ).
A. B. C. D.
4.在平面直角坐标系中,若有一点P(2,1)向上平移3个单位或向左平移4个单位,恰
好都在直线y=kx+b上,则k的值是( )
A. B. C. D. 2
5.已知一次函数y=kx+2的图象经过点(3,-3),则k值为( )
A. B. C. D.
6.已知变量y与x之间的函数关系的图象如图,它的解析式是( )
( http: / / www.21cnjy.com )
A. y= x+2(0≤x≤3) B. y= x+2 C. y= x+2(0≤x≤3) D. y= x+2
7.一次函数的图象交x轴于(2,0),交y轴于(0,3),当函数值大于0时,x的取值范围是( )2·1·c·n·j·y
A. x>2 B. x<2 C. x>3 D. x<3
8.已知一次函数的图象过点(0,3),且与两坐标轴所围成的三角形面积为3,则其表达式为( )
A. y=1.5x+3 B. y=-1.5x+3
C. y=1.5x+3或y=-1.5x+3 D. y=1.5x-3或y=-1.5x-3
9.如图,过点的一次函数的图象与正比例函数的图象相交于点,则这个一次函数的解析式是( ).【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
A. B. C. D.
二、填空题
10.直线关于y轴对称的直线的解析式_________.
11.已知某一次函数与直线平行,且经过点,则这个一次函数解析式是__________.
12.若一次函数y=kx+b,当-3≤x≤1时,对应的y值满足1≤y≤9,则一次函数的解析式为____________.【来源:21cnj*y.co*m】
13.若点在一次函数的图象上,则的值为__________.
14.请写出一个经过点且y随x的增大而减小的一次函数表达式 ________________.
15.如图,将直线y=-x沿y轴向下平移后 ( http: / / www.21cnjy.com )的直线恰好经过点A(2,-4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为____.
( http: / / www.21cnjy.com )
三、解答题
16.已知一次函数在时,,且它的图象与轴交点的横坐标是,求这个一次函数的解析式.
17.已知y=(m+1)x2-|m|+n+4是y关于x的一次函数.
(1)求m、n的值;
(2)当m、n满足什么条件时,此函数的图象经过坐标原点?
18.已知一次函数y=kx﹣4,当x=2时,y=﹣3.
(1)求一次函数的解析式;
(2)将该函数的图象向上平移6个单位,求平移后的图象与x轴的交点的坐标.
19.“边疆宣讲团”从招待 ( http: / / www.21cnjy.com )所出发,动身前往某边防哨所去为哨所官兵宣讲“十九大”精神.若按照他们出发时的速度匀速直线行进,则刚好在约定的时间准点到达哨所; 可天有不测风云! 因道路交通事故,他们中途被迫停留了半小时; 为按约定时【版权所有:21教育】
间准点到达哨所,他们后来加快速度但仍保 ( http: / / www.21cnjy.com )持匀速直线行进,结果正好准点到达哨所.如图7,是他们离哨所的距离y(km)与所用时间x(h)之间的部分函数图象.根据图象,解答下列问题:
(1)求CD所在直线的表达式;
(2)求招待所离哨所的距离.
( http: / / www.21cnjy.com )
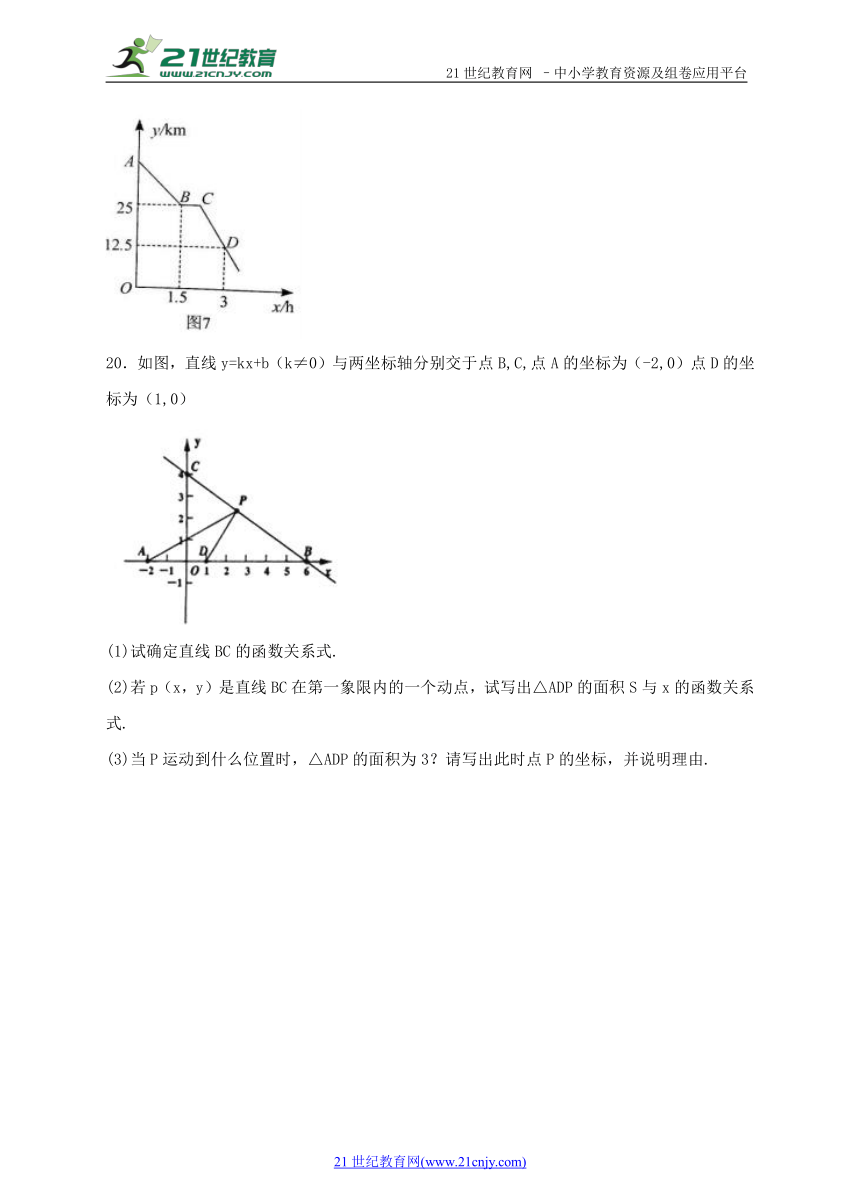
20.如图,直线y=kx+b(k≠0)与两坐标轴分别交于点B,C,点A的坐标为(-2,0)点D的坐标为(1,0)21教育名师原创作品
( http: / / www.21cnjy.com )
(1)试确定直线BC的函数关系式.
(2)若p(x,y)是直线BC在第一象限内的一个动点,试写出△ADP的面积S与x的函数关系式.
(3)当P运动到什么位置时,△ADP的面积为3?请写出此时点P的坐标,并说明理由.
参考答案
1.B
【解析】试题解析:∵直线与平行,
( http: / / www.21cnjy.com )
把代入得 解得
∴的表达式是
故选B.
2.B
【解析】解:设直线l的函数关系式为y=kx+b,
∵直线l过原点,
∴b=0,
∵直线与直线l平行,
∴k=,
∴这条直线l的函数关系式为y=x,
故选:B.
点睛:此题主要考查了两条直线平行问题关键是掌握直线y=kx+b,(k≠0,且k,b为常数),当k相同,且b不相等,图象平行.21世纪教育网版权所有
3.B
【解析】
解得
将代入,
,
.
故选.
4.B
【解析】试题解析:点P(2,1)向上平移3个单位或者向左平移4个单位的坐标为(2,4)或(-2,1),21*cnjy*com
把(2,4)和(-2,1)代入y=kx+b,可得: ,
解得:,
故选C.
5.B
【解析】把点(3,-3)代入函数解析式,得到关于k的方程,解之即可得出k值.
解:把(3,-3)代入y=kx+2得,
解得.
故选B.
点睛:本题考查用待定系数法求一次函数解析式.将函数图象上的点代入函数解析式并准确求解是解题的关键.
6.A
【解析】从函数图象上可以看出,这条线段经过点(3,0)和(0,2),
所以可以设其函数关系式为y=kx+2.
再把点(3,0)代入求得k= ,
所以其函数关系式为y= x+2,且自变量的取值范围为0 x 3.
故选:A.
7.B
【解析】设一次函数的解析式为y=kx+b
∵一次函数的图象交x轴于(2,0),交y轴于(0,3),代入函数的解析式,
得,解得,
∴一次函数的解析式为y= x+3,
令y>0,解得x<2
故选:B.
8.C
【解析】设一次函数解析式为y=kx+b(k≠0).
∵点A(0,3)在一次函数图象上,
∴0+b=3,即b=3.
则一次函数解析式为y=kx+3.
令y=0,则x=- ,即直线与x轴交点的横坐标为-.
∵直线与坐标轴围成的三角形的面积为3,
∴×|-|×3=3.
解得k=±1.5.
∴一次函数解析式为y=1.5x+3或y=-1.5x+3.
故选C.
9.D
【解析】当x=1时,y=2x=2,∴B(1,2),
∵过点, ,
∴,
故选.
10.y=2x+1
【解析】从上取两点:(0,1)和(1,-1),
则(0,1)和(1,-1)关于y轴对称的两点是:(0,1)和(-1,-1).
设所求函数关系式是:,
把(0,1)和(-1,-1)代入得
,
∴,
∴.
11.
【解析】设一次函数解析式
∵与平行,
∴,
∴.
∵一次函数经过,
∴,,
∴.
12.y=2x+7或y=-2x+3
【解析】解:分两种情况讨论:
(1)当k>0时, ,解得:,此时y=2x+7;
(2)当k<0时, ,解得:,此时y=-2x+3.
综上所述:所求的函数解析式为:y=2x+7或y=-2x+3.
点睛:本题主要考查待定系数法求一次函数的解析式的知识,解答本题的关键是熟练掌握一次函数的性质:在定义域上是单调函数,本题难度不大.21cnjy.com
13.2
【解析】∵在一次函数,
∴,
∴m=2.
故答案为:2.
14.y=-x+3,等.(答案不唯一)
【解析】由题意分析可知,这样的函数有很多,只要这个一次函数中,且其图象过点(-1,2)就可以,如一次函数: 等.21·世纪*教育网
故本题答案不唯一,如等.
15.(,0)
【解析】试题分析:如图所示,作点B关于x轴对称的点B',连接AB',交x轴于P,则点P即为所求,
( http: / / www.21cnjy.com )
设直线y=-x沿y轴向下平移后的直线解析式为y=-x+a,
把A(2,-4)代入可得,a=-2,
∴平移后的直线为y=-x-2,
令x=0,则y=-2,即B(0,-2)
∴B'(0,2),
设直线AB'的解析式为y=kx+b,
把A(2,-4),B'(0,2)代入可得,
,
解得,
∴直线AB'的解析式为y=-3x+2,
令y=0,则x=,
∴P(,0),
故答案为:(,0).
点睛:本题属于最短路线问题,主要考 ( http: / / www.21cnjy.com )查了一次函数图象与几何变换的运用,解决问题的关键是掌握:在直线l上的同侧有两个点A、B,在直线l上有到A、B的距离之和最短的点存在,可以通过轴对称来确定,即作出其中一点关于直线l的对称点,对称点与另一点的连线与直线l的交点就是所要找的点.www-2-1-cnjy-com
16.
【解析】试题分析:把,和,代入到,得到关于a和b的二元一次方程组,解方程组求出a、b的值即可得到结论.2-1-c-n-j-y
∵
时,
且与轴交点为,
∴,
解得,
∴.
点睛:本题主要考查的是利用待定系数 ( http: / / www.21cnjy.com )法确定函数解析式.利用待定系数法求函数解析式的一般步骤:①设出含有待定系数的解析式;②把已知条件(自变量与函数的对应值)代入解析式,得到关于待定系数的方程(组);③解方程(组),求出待定系数;④将求得的待定系数的值代回所设的解析式.21*cnjy*com
17.(1) m=1,n为任意实数;(2) m=1,n=-4
【解析】试题分析:(1)根据一次函数的定义, ( http: / / www.21cnjy.com )即可得出关于m的一元一次不等式以及含绝对值符号的一元一次方程,解之即可得出结论;
(2)根据一次函数图象上点的坐标特征,即可得出关于n的一元一次方程,解之即可得出结论.【出处:21教育名师】
试题解析:
(1)∵y=(m+1)x2-|m|+n+4是y关于x的一次函数,
∴m+1≠0,2-|m|=1,解得m=1.
∴m=1,n为任意实数.
(2)∵y=2x+n+4的图象过原点,
∴n+4=0,解得n=-4.
∴当m=1,n=-4时,此函数的图象经过坐标原点.
18.(1)y=x﹣4;(2)(﹣4,0).
【解析】试题分析:(1)把 ( http: / / www.21cnjy.com )已知条件代入函数解析式可求得k的值,则可求得一次函数解析式;
(2)利用平移的规律可求得平移后的解析式,再令y=0可求得与x轴的交点坐标.
试题解析:
(1)由题意可得2k﹣4=﹣3,解得k=,
∴一次函数解析式为y=x﹣4;
(2)把该函数图象向上平移6个单位可得y=x﹣4+6=x+2,
令y=0可得x+2=0,解得x=﹣4,
∴平移后图象与x轴的交点坐标为(﹣4,0).
19.(1)CD的解析式为:y=-12.5+50;(2)招待所与哨所之间距离为40km
【解析】试题分析:(1)根据点C、D的坐标利用待定系数法,即可求出CD所在直线的表达式;
(2)利用一次函数图象上 ( http: / / www.21cnjy.com )点的坐标特征可得出原计划4小时到达,结合点B的坐标利用待定系数法,即可求出AB所在直线的表达式,代入x=0即可得出点A的坐标,此题得解.
试题解析:(1)设CD所在直线的表达式为y=kx+b(k≠0),
将点C(2,25)、D(3,12.5)代入y=kx+b,
得,解得:,
∴CD所在直线的表达式为y=﹣12.5x+50.
(2)当y=0时,有﹣12.5x+50=0,
解得:x=4,
∴原计划4小时到达.
设AB所在直线的表达式为y=mx+n(m≠0),
将点(1.5,25)、(4,0)代入y=mx+n,
得,解得:,
∴AB所在直线的表达式为y=﹣10x+40.
当x=0时,y=﹣10x+40=40,
∴点A的坐标为(0,40),
∴招待所离哨所的距离为40km.
点睛:本题考查了一次函数的应用、待定系 ( http: / / www.21cnjy.com )数法求一次函数解析式以及一次函数图象上点的坐标特征,解题的关键是:(1)利用待定系数法求出CD所在直线的表达式;(2)利用待定系数法求出AB所在直线的表达式.21教育网
20.(1)y=-x+4;(2) S=-x+6;(3) (3,2)
【解析】(1)运用待定系数法即可求出解析式;
(2)利用三角形面积公式即可建立函数关系式;
(3)利用(2)中的函数关系式即可得出答案.
解:(1)设直线BC的函数关系式为y=kx+b(k≠0),
由题意,得方程组,,
解得,
所以,函数y与x的函数关系式为y=-x+4;
(2)由题意,P(x,y)是直线BC在第一象限的点,
∴y>0,且y=-x+4,
又,点A的坐标为(-2,0),点D的坐标为(1,0),
∴AD=3,
∴S△ADP=×3×〔-x+4 〕=-x+6,
即S=-x+6;
(3)当S=3时,
-x+6=3,
解得x=3,
所以y=-×3+4=2,
此时,点P的坐标为(3,2).
点睛:本题主要考查一次函数与几何图形的关系.将点的坐标转化为线段的长是解题的关键.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
19.2.2 一次函数(3)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.设一次函数为y=kx+b,再依条件确定解析式中的未知系数,从而具体写出这个式子的方法叫做待定系数法. 21·cn·jy·com
2.一次函数y=kx+b中有k、b两个待 ( http: / / www.21cnjy.com )定系数,故利用待定系数法时需要根据条件列二元一次方程组(以k和b 为未知数),解方程组就能具体写出一次函数的解析式.
3.用待定系数法求函数解析式的一般步骤:设出含有待定系数的函数解析式;把已知条件(自变量与函数的对应值)代入解析式,得到关于待定系数的方程或方程组;解方程或方程组,求出待定系数; 将求得的待定系数代回所设的解析式.www.21-cn-jy.com
基础知识和能力拓展精练
一、选择题
1.已知直线y=kx+b与y=2x﹣5平行且经过点(1,3),则y=kx+b的表达式是( )
A. y=x+2 B. y=2x+1 C. y=2x+2 D. y=2x+3
2.已知直线与一条经过原点的直线l平行,则这条直线l的函数关系式为( )
A. B. C. D. y=2x
3.已知函数,,的图象交于一点,则值为( ).
A. B. C. D.
4.在平面直角坐标系中,若有一点P(2,1)向上平移3个单位或向左平移4个单位,恰
好都在直线y=kx+b上,则k的值是( )
A. B. C. D. 2
5.已知一次函数y=kx+2的图象经过点(3,-3),则k值为( )
A. B. C. D.
6.已知变量y与x之间的函数关系的图象如图,它的解析式是( )
( http: / / www.21cnjy.com )
A. y= x+2(0≤x≤3) B. y= x+2 C. y= x+2(0≤x≤3) D. y= x+2
7.一次函数的图象交x轴于(2,0),交y轴于(0,3),当函数值大于0时,x的取值范围是( )2·1·c·n·j·y
A. x>2 B. x<2 C. x>3 D. x<3
8.已知一次函数的图象过点(0,3),且与两坐标轴所围成的三角形面积为3,则其表达式为( )
A. y=1.5x+3 B. y=-1.5x+3
C. y=1.5x+3或y=-1.5x+3 D. y=1.5x-3或y=-1.5x-3
9.如图,过点的一次函数的图象与正比例函数的图象相交于点,则这个一次函数的解析式是( ).【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
A. B. C. D.
二、填空题
10.直线关于y轴对称的直线的解析式_________.
11.已知某一次函数与直线平行,且经过点,则这个一次函数解析式是__________.
12.若一次函数y=kx+b,当-3≤x≤1时,对应的y值满足1≤y≤9,则一次函数的解析式为____________.【来源:21cnj*y.co*m】
13.若点在一次函数的图象上,则的值为__________.
14.请写出一个经过点且y随x的增大而减小的一次函数表达式 ________________.
15.如图,将直线y=-x沿y轴向下平移后 ( http: / / www.21cnjy.com )的直线恰好经过点A(2,-4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为____.
( http: / / www.21cnjy.com )
三、解答题
16.已知一次函数在时,,且它的图象与轴交点的横坐标是,求这个一次函数的解析式.
17.已知y=(m+1)x2-|m|+n+4是y关于x的一次函数.
(1)求m、n的值;
(2)当m、n满足什么条件时,此函数的图象经过坐标原点?
18.已知一次函数y=kx﹣4,当x=2时,y=﹣3.
(1)求一次函数的解析式;
(2)将该函数的图象向上平移6个单位,求平移后的图象与x轴的交点的坐标.
19.“边疆宣讲团”从招待 ( http: / / www.21cnjy.com )所出发,动身前往某边防哨所去为哨所官兵宣讲“十九大”精神.若按照他们出发时的速度匀速直线行进,则刚好在约定的时间准点到达哨所; 可天有不测风云! 因道路交通事故,他们中途被迫停留了半小时; 为按约定时【版权所有:21教育】
间准点到达哨所,他们后来加快速度但仍保 ( http: / / www.21cnjy.com )持匀速直线行进,结果正好准点到达哨所.如图7,是他们离哨所的距离y(km)与所用时间x(h)之间的部分函数图象.根据图象,解答下列问题:
(1)求CD所在直线的表达式;
(2)求招待所离哨所的距离.
( http: / / www.21cnjy.com )
20.如图,直线y=kx+b(k≠0)与两坐标轴分别交于点B,C,点A的坐标为(-2,0)点D的坐标为(1,0)21教育名师原创作品
( http: / / www.21cnjy.com )
(1)试确定直线BC的函数关系式.
(2)若p(x,y)是直线BC在第一象限内的一个动点,试写出△ADP的面积S与x的函数关系式.
(3)当P运动到什么位置时,△ADP的面积为3?请写出此时点P的坐标,并说明理由.
参考答案
1.B
【解析】试题解析:∵直线与平行,
( http: / / www.21cnjy.com )
把代入得 解得
∴的表达式是
故选B.
2.B
【解析】解:设直线l的函数关系式为y=kx+b,
∵直线l过原点,
∴b=0,
∵直线与直线l平行,
∴k=,
∴这条直线l的函数关系式为y=x,
故选:B.
点睛:此题主要考查了两条直线平行问题关键是掌握直线y=kx+b,(k≠0,且k,b为常数),当k相同,且b不相等,图象平行.21世纪教育网版权所有
3.B
【解析】
解得
将代入,
,
.
故选.
4.B
【解析】试题解析:点P(2,1)向上平移3个单位或者向左平移4个单位的坐标为(2,4)或(-2,1),21*cnjy*com
把(2,4)和(-2,1)代入y=kx+b,可得: ,
解得:,
故选C.
5.B
【解析】把点(3,-3)代入函数解析式,得到关于k的方程,解之即可得出k值.
解:把(3,-3)代入y=kx+2得,
解得.
故选B.
点睛:本题考查用待定系数法求一次函数解析式.将函数图象上的点代入函数解析式并准确求解是解题的关键.
6.A
【解析】从函数图象上可以看出,这条线段经过点(3,0)和(0,2),
所以可以设其函数关系式为y=kx+2.
再把点(3,0)代入求得k= ,
所以其函数关系式为y= x+2,且自变量的取值范围为0 x 3.
故选:A.
7.B
【解析】设一次函数的解析式为y=kx+b
∵一次函数的图象交x轴于(2,0),交y轴于(0,3),代入函数的解析式,
得,解得,
∴一次函数的解析式为y= x+3,
令y>0,解得x<2
故选:B.
8.C
【解析】设一次函数解析式为y=kx+b(k≠0).
∵点A(0,3)在一次函数图象上,
∴0+b=3,即b=3.
则一次函数解析式为y=kx+3.
令y=0,则x=- ,即直线与x轴交点的横坐标为-.
∵直线与坐标轴围成的三角形的面积为3,
∴×|-|×3=3.
解得k=±1.5.
∴一次函数解析式为y=1.5x+3或y=-1.5x+3.
故选C.
9.D
【解析】当x=1时,y=2x=2,∴B(1,2),
∵过点, ,
∴,
故选.
10.y=2x+1
【解析】从上取两点:(0,1)和(1,-1),
则(0,1)和(1,-1)关于y轴对称的两点是:(0,1)和(-1,-1).
设所求函数关系式是:,
把(0,1)和(-1,-1)代入得
,
∴,
∴.
11.
【解析】设一次函数解析式
∵与平行,
∴,
∴.
∵一次函数经过,
∴,,
∴.
12.y=2x+7或y=-2x+3
【解析】解:分两种情况讨论:
(1)当k>0时, ,解得:,此时y=2x+7;
(2)当k<0时, ,解得:,此时y=-2x+3.
综上所述:所求的函数解析式为:y=2x+7或y=-2x+3.
点睛:本题主要考查待定系数法求一次函数的解析式的知识,解答本题的关键是熟练掌握一次函数的性质:在定义域上是单调函数,本题难度不大.21cnjy.com
13.2
【解析】∵在一次函数,
∴,
∴m=2.
故答案为:2.
14.y=-x+3,等.(答案不唯一)
【解析】由题意分析可知,这样的函数有很多,只要这个一次函数中,且其图象过点(-1,2)就可以,如一次函数: 等.21·世纪*教育网
故本题答案不唯一,如等.
15.(,0)
【解析】试题分析:如图所示,作点B关于x轴对称的点B',连接AB',交x轴于P,则点P即为所求,
( http: / / www.21cnjy.com )
设直线y=-x沿y轴向下平移后的直线解析式为y=-x+a,
把A(2,-4)代入可得,a=-2,
∴平移后的直线为y=-x-2,
令x=0,则y=-2,即B(0,-2)
∴B'(0,2),
设直线AB'的解析式为y=kx+b,
把A(2,-4),B'(0,2)代入可得,
,
解得,
∴直线AB'的解析式为y=-3x+2,
令y=0,则x=,
∴P(,0),
故答案为:(,0).
点睛:本题属于最短路线问题,主要考 ( http: / / www.21cnjy.com )查了一次函数图象与几何变换的运用,解决问题的关键是掌握:在直线l上的同侧有两个点A、B,在直线l上有到A、B的距离之和最短的点存在,可以通过轴对称来确定,即作出其中一点关于直线l的对称点,对称点与另一点的连线与直线l的交点就是所要找的点.www-2-1-cnjy-com
16.
【解析】试题分析:把,和,代入到,得到关于a和b的二元一次方程组,解方程组求出a、b的值即可得到结论.2-1-c-n-j-y
∵
时,
且与轴交点为,
∴,
解得,
∴.
点睛:本题主要考查的是利用待定系数 ( http: / / www.21cnjy.com )法确定函数解析式.利用待定系数法求函数解析式的一般步骤:①设出含有待定系数的解析式;②把已知条件(自变量与函数的对应值)代入解析式,得到关于待定系数的方程(组);③解方程(组),求出待定系数;④将求得的待定系数的值代回所设的解析式.21*cnjy*com
17.(1) m=1,n为任意实数;(2) m=1,n=-4
【解析】试题分析:(1)根据一次函数的定义, ( http: / / www.21cnjy.com )即可得出关于m的一元一次不等式以及含绝对值符号的一元一次方程,解之即可得出结论;
(2)根据一次函数图象上点的坐标特征,即可得出关于n的一元一次方程,解之即可得出结论.【出处:21教育名师】
试题解析:
(1)∵y=(m+1)x2-|m|+n+4是y关于x的一次函数,
∴m+1≠0,2-|m|=1,解得m=1.
∴m=1,n为任意实数.
(2)∵y=2x+n+4的图象过原点,
∴n+4=0,解得n=-4.
∴当m=1,n=-4时,此函数的图象经过坐标原点.
18.(1)y=x﹣4;(2)(﹣4,0).
【解析】试题分析:(1)把 ( http: / / www.21cnjy.com )已知条件代入函数解析式可求得k的值,则可求得一次函数解析式;
(2)利用平移的规律可求得平移后的解析式,再令y=0可求得与x轴的交点坐标.
试题解析:
(1)由题意可得2k﹣4=﹣3,解得k=,
∴一次函数解析式为y=x﹣4;
(2)把该函数图象向上平移6个单位可得y=x﹣4+6=x+2,
令y=0可得x+2=0,解得x=﹣4,
∴平移后图象与x轴的交点坐标为(﹣4,0).
19.(1)CD的解析式为:y=-12.5+50;(2)招待所与哨所之间距离为40km
【解析】试题分析:(1)根据点C、D的坐标利用待定系数法,即可求出CD所在直线的表达式;
(2)利用一次函数图象上 ( http: / / www.21cnjy.com )点的坐标特征可得出原计划4小时到达,结合点B的坐标利用待定系数法,即可求出AB所在直线的表达式,代入x=0即可得出点A的坐标,此题得解.
试题解析:(1)设CD所在直线的表达式为y=kx+b(k≠0),
将点C(2,25)、D(3,12.5)代入y=kx+b,
得,解得:,
∴CD所在直线的表达式为y=﹣12.5x+50.
(2)当y=0时,有﹣12.5x+50=0,
解得:x=4,
∴原计划4小时到达.
设AB所在直线的表达式为y=mx+n(m≠0),
将点(1.5,25)、(4,0)代入y=mx+n,
得,解得:,
∴AB所在直线的表达式为y=﹣10x+40.
当x=0时,y=﹣10x+40=40,
∴点A的坐标为(0,40),
∴招待所离哨所的距离为40km.
点睛:本题考查了一次函数的应用、待定系 ( http: / / www.21cnjy.com )数法求一次函数解析式以及一次函数图象上点的坐标特征,解题的关键是:(1)利用待定系数法求出CD所在直线的表达式;(2)利用待定系数法求出AB所在直线的表达式.21教育网
20.(1)y=-x+4;(2) S=-x+6;(3) (3,2)
【解析】(1)运用待定系数法即可求出解析式;
(2)利用三角形面积公式即可建立函数关系式;
(3)利用(2)中的函数关系式即可得出答案.
解:(1)设直线BC的函数关系式为y=kx+b(k≠0),
由题意,得方程组,,
解得,
所以,函数y与x的函数关系式为y=-x+4;
(2)由题意,P(x,y)是直线BC在第一象限的点,
∴y>0,且y=-x+4,
又,点A的坐标为(-2,0),点D的坐标为(1,0),
∴AD=3,
∴S△ADP=×3×〔-x+4 〕=-x+6,
即S=-x+6;
(3)当S=3时,
-x+6=3,
解得x=3,
所以y=-×3+4=2,
此时,点P的坐标为(3,2).
点睛:本题主要考查一次函数与几何图形的关系.将点的坐标转化为线段的长是解题的关键.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
