4.3 探索三角形全等的条件(1)同步练习
文档属性
| 名称 | 4.3 探索三角形全等的条件(1)同步练习 |  | |
| 格式 | docx | ||
| 文件大小 | 467.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-29 16:34:21 | ||
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
4.3 探索三角形全等的条件(1)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.三边对应相等的两个三角形全等,简写成边边边(或SSS).
2.三角形具有稳定性,四边形具有不稳定性 .
3.三个内角相等的两个三角形不一定全等
全等基础知识和能力拓展精练
一、选择题
1.如图,AB=AC,D为BC边上一点,且BD=DC,则下列结论不正确的是( )
A. △ABD≌△ACD B. ∠ADB=90° C. ∠BAD=∠B D. AD平分∠BAC
2.如图,AB=CD,AD=CB,那么下列结论中错误的是( )
A. ∠A=∠C B. AB=AD C. AD∥BC D. AB∥CD
3.如图,点A,E,B,F在一条直线上,在△ABC和△FED中,AC=FD,BC=DE,要利用“SSS”来判定△ABC≌△FED时,下面4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE.可利用的是( )
A. ①或② B. ②或③ C. ③或① D. ①或④
4.△ABC和△DEF中,AB=2,BC=3,CA=4,DE=4,EF=3,要使△ABC与△DEF全等,则DF等于( )
A. 2 B. 3 C. 4 D. 不能确定
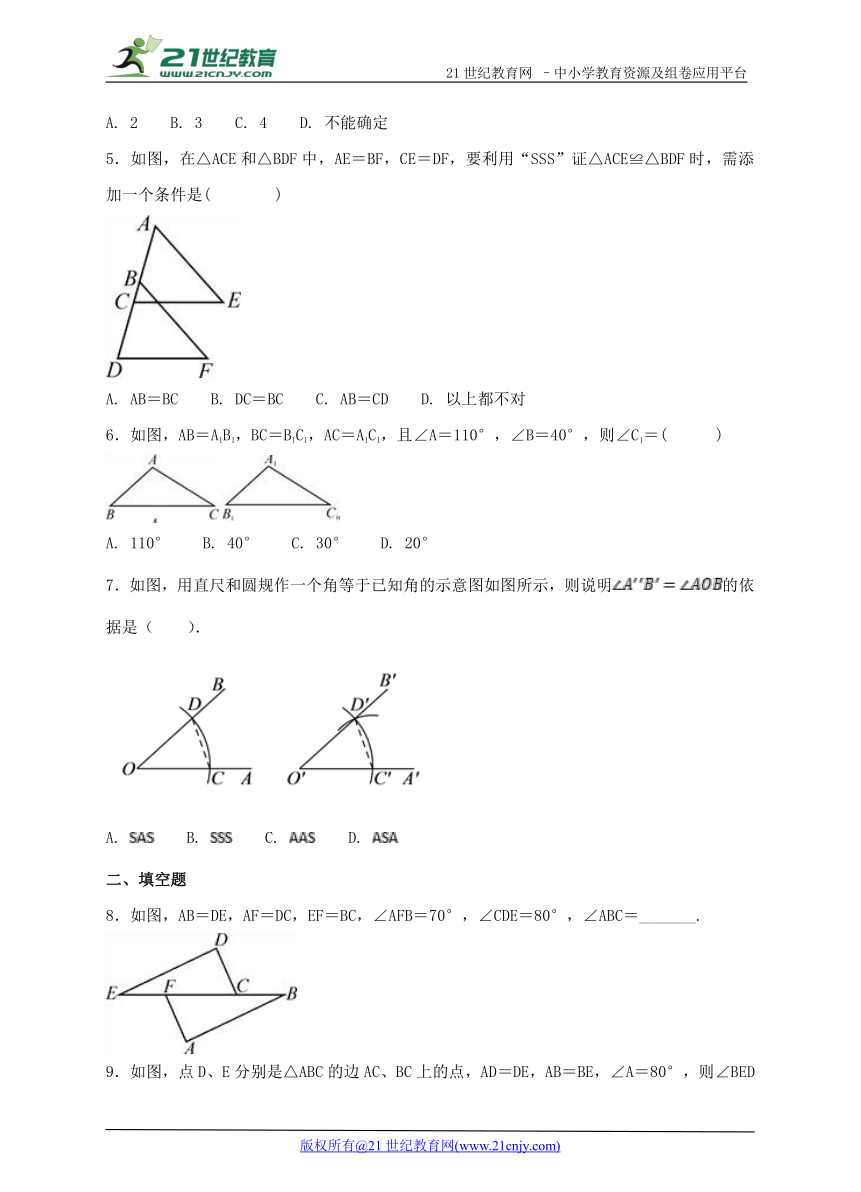
5.如图,在△ACE和△BDF中,AE=BF,CE=DF,要利用“SSS”证△ACE≌△BDF时,需添加一个条件是( )
A. AB=BC B. DC=BC C. AB=CD D. 以上都不对
6.如图,AB=A1B1,BC=B1C1,AC=A1C1,且∠A=110°,∠B=40°,则∠C1=( )
A. 110° B. 40° C. 30° D. 20°
7.如图,用直尺和圆规作一个角等于已知角的示意图如图所示,则说明的依据是( ).
A. B. C. D.
二、填空题
8.如图,AB=DE,AF=DC,EF=BC,∠AFB=70°,∠CDE=80°,∠ABC=_______.
9.如图,点D、E分别是△ABC的边AC、BC上的点,AD=DE,AB=BE,∠A=80°,则∠BED=____°.
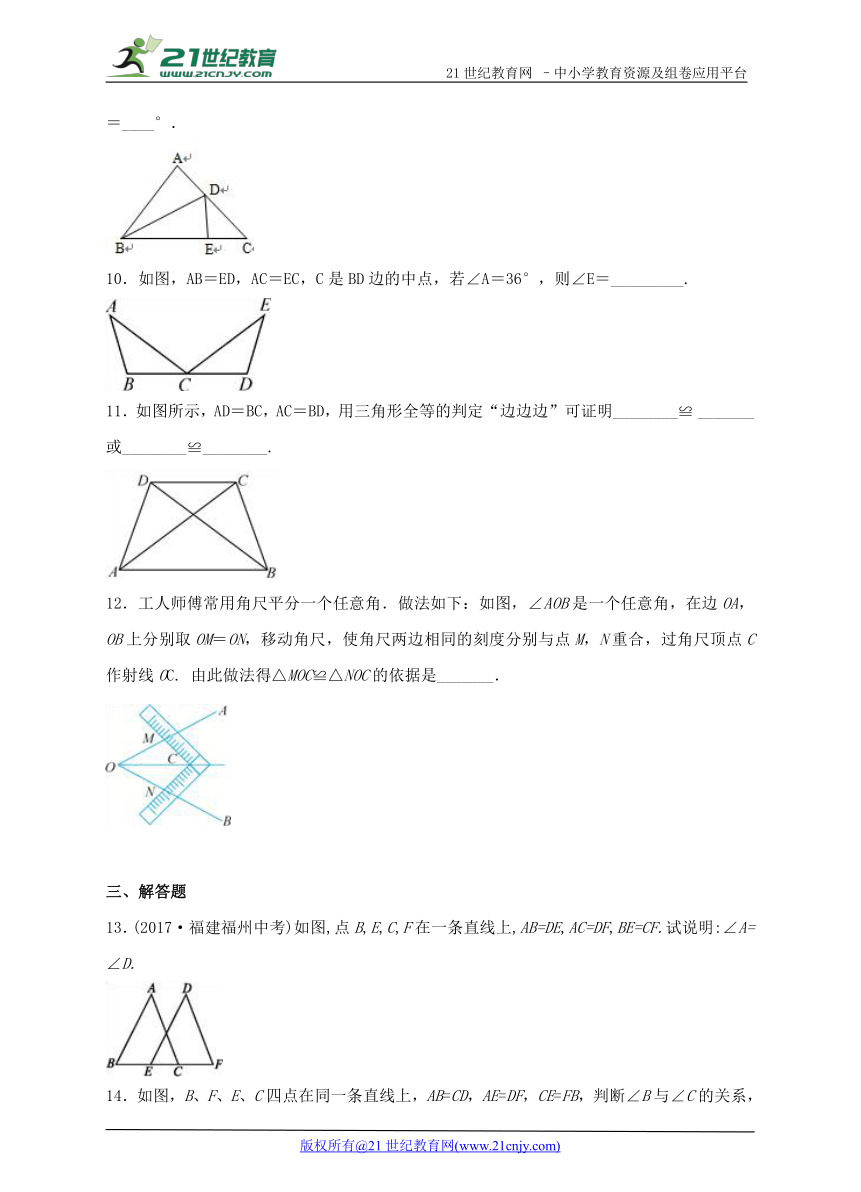
10.如图,AB=ED,AC=EC,C是BD边的中点,若∠A=36°,则∠E=_________.
11.如图所示,AD=BC,AC=BD,用三角形全等的判定“边边边”可证明________≌ _______或________≌________.
12.工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C作射线OC. 由此做法得△MOC≌△NOC的依据是_______.
三、解答题
13.(2017·福建福州中考)如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.试说明:∠A=∠D.
14.如图,B、F、E、C四点在同一条直线上,AB=CD,AE=DF,CE=FB,判断∠B与∠C的关系,并证明.
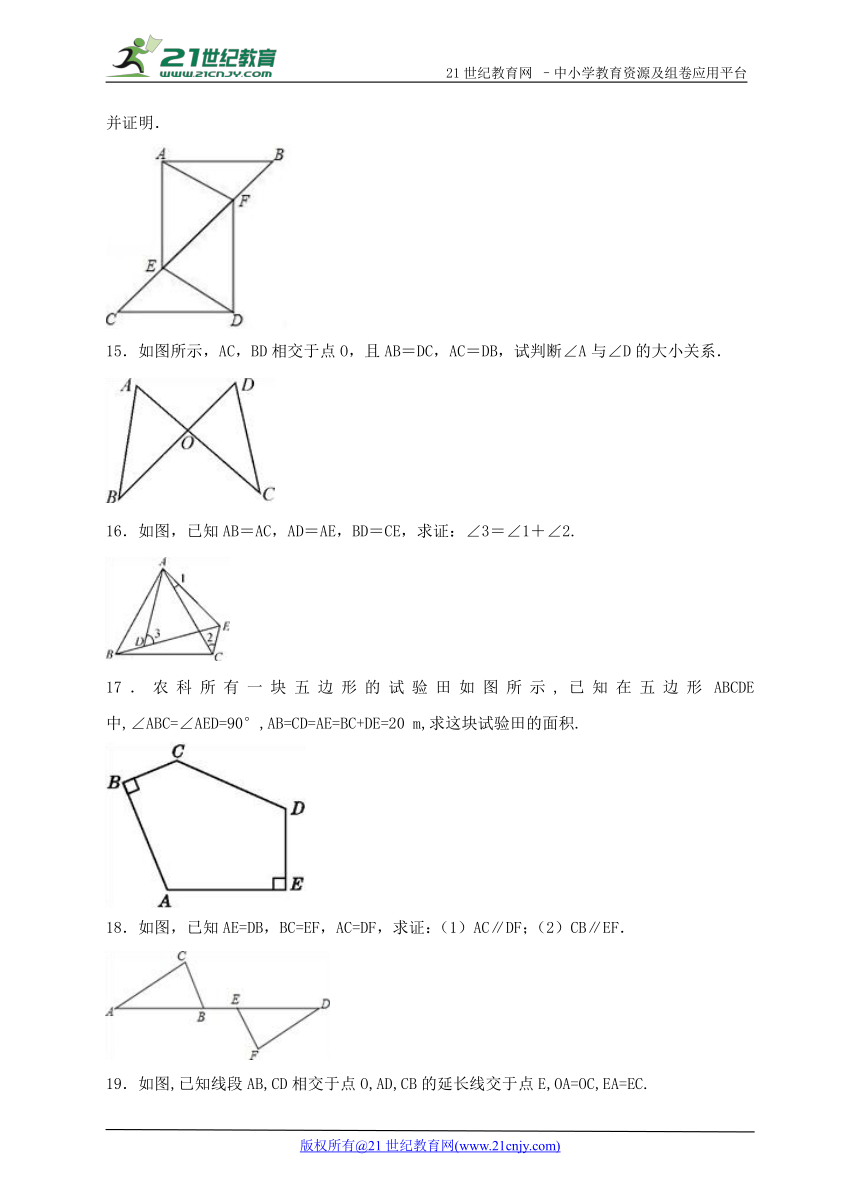
15.如图所示,AC,BD相交于点O,且AB=DC,AC=DB,试判断∠A与∠D的大小关系.
16.如图,已知AB=AC,AD=AE,BD=CE,求证:∠3=∠1+∠2.
17.农科所有一块五边形的试验田如图所示,已知在五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=20 m,求这块试验田的面积.
18.如图,已知AE=DB,BC=EF,AC=DF,求证:(1)AC∥DF;(2)CB∥EF.
19.如图,已知线段AB,CD相交于点O,AD,CB的延长线交于点E,OA=OC,EA=EC.
(1)试说明:∠A=∠C;
(2)在(1)的解答过程中,需要作辅助线,它的意图是什么
参考答案
1.C
【解析】试题解析:在与中,
∴≌,
又
∴ AD平分
故选C.
2.B
【解析】∵在△ABD和△CDB中,
,
∴△ABD≌△CDB,
∴∠ADB=∠CBD,∠ABD=∠CDB,∠A=∠C
∴AD∥BC,AB∥CD,
∴A、C、D选项正确.
故选:B.
3.A
【解析】试题解析:由题意可得,要用SSS进行△ABC和△FED全等的判定,需要AB=FE,
若添加①AE=FB,则可得AE+BE=FB+BE,即AB=FE,
故①可以;
若添加AB=FE,则可直接证明两三角形的全等,故②可以,
若添加AE=BE,或BF=BE,均不能得出AB=FE,不可以利用SSS进行全等的证明,故③④不可以.
故选A.
4.A
【解析】试题解析:根据题意得: 所以如果要使与 全等,那么
故选A.
5.C
【解析】试题解析:要利用“SSS”证明≌时,需
故选C.
6.C
【解析】试题解析:∵在中,
∴≌ ,
故选C.
7.B
【解析】由作图过程可知:,,
在和中,
,
∴≌,
∴.
即能说明:的依据是“SSS”.
故选B.
8.30°
【解析】试题解析:∵CF=BE,
∴CF+EF=BE+EF,
∴CE=BF,
在△AFB和△DEC中,
∴△AFB≌△DEC(SSS),
∴在△AFB中,
故答案为:
9.80
【解析】由边边边定理可得
10.36°
【解析】试题解析:∵C是BD的中点,
∴BC=CD,
∵AB=ED,AC=EC,
∴△ABC≌△EDC(SSS),
故答案为:
11. △ADC, △BCD , △ADB, △BCA
【解析】试题解析:在△ADC和△BCD中;
∴△ADC≌△BCD(SSS).
在△ADB和△BCA中;
∴△ADB≌△BCA(SSS).
故答案为:△ADC,△BCD;△ADB,△BCA.
点睛:三条边对应相等,两个三角形全等.
12.SSS
【解析】由作图可知,OM=ON,CM=CN,OC=OC,所以△MOC≌△NOC(SSS),故答案为SSS.
13.理由见解析.
【解析】试题分析:根据题意得出BC=EF,然后结合已知条件得出△ABC和△DEF全等,从而得出答案.
试题解析:因为BE=CF,所以BE+CE=CF+CE, 所以BC=EF.
在△ABC和△DEF中, 所以△ABC≌△DEF(SSS),所以∠A=∠D.
14.∠B=∠C.
【解析】试题分析:根据已知条件证明△ABE≌△DCF,根据全等三角形的性质即可得结论.
试题解析:
结论:∠B=∠C.
理由:∵CE=BF,
∴CE+EF=EF+BF,即CF=BE,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(SSS),
∴∠B=∠C.
15.证明见解析
【解析】试题分析:连接BC.根据SSS证明≌,即可证明.
试题解析:证明:连接BC.
在和中,
∴≌(SSS),
16.证明见解析
【解析】试题分析:根据全等三角形的判定定理SSS证得对应角相等,然后通过外角的性质即可得到结论.
试题解析:证明:在△ABD与△ACE中,
∴△ABD≌△ACE,
∴∠BAD=∠1,∠ABD=∠2,
∵∠3=∠BAD+∠ABD,
∴∠3=∠1+∠2.
17.400m2.
【解析】试题分析:可延长DE至F,使EF=BC,可得△ABC≌△AEF,连AC,AD,AF,可将五边形ABCDE的面积转化为两个△ADF的面积,进而求出结论.
试题解析:如图,延长DE至点F,使EF=BC,连接AC,AD,AF.易得CD=FD.
因为
所以△ABC≌△AEF(SAS).
所以AC=AF.
在△ACD与△AFD中,因为
所以△ACD≌△AFD(SSS).
所以五边形ABCDE的面积是
2S△ADF=2×·DF·AE=2××20×20=400(m2).
18.(1)证明见解析(2)证明见解析
【解析】试题分析:(1)由SSS证明△ABC≌△DEF,得出对应角相等∠A=∠D,∠ABC=∠DEF,由内错角相等即可得出结论;
(2)由(1)得:∠ABC=∠DEF,得出∠CBE=∠FEB,由内错角相等即可得出结论.
试题解析:(1)∵AE=DB,
∴AE-BE=DB-BE,
即AB=DE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS),
∴∠A=∠D,∠ABC=∠DEF,
∴AC∥DF;
(2)由(1)得:∠ABC=∠DEF,
∴∠CBE=∠FEB,
∴CB∥EF.
19.(1)见解析;(2)构造全等三角形.
【解析】分析:(1)根据题意,没有证明两三角形全等的条件,所以要作条辅助线,连接OE;然后就可以利用SSS全等判定定理证明两三角形全等,继而∠A=∠C,本题即可证明(1),(2),说明OE的意义即可.
本题解析:
(1)如图,连接OE.
在△EAO和△ECO中,
所以△EAO≌△ECO(SSS).
所以∠A=∠C(全等三角形的对应角相等).
(2)构造全等三角形.
意图:本题运用了构造法,通过连接OE,构造△OAE,△OCE,将欲说明相等的∠A,∠C分别置于这两个三角形中,然后通过说明全等可得∠A=∠C.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
版权所有@21世纪教育网(www.21cnjy.com)
4.3 探索三角形全等的条件(1)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.三边对应相等的两个三角形全等,简写成边边边(或SSS).
2.三角形具有稳定性,四边形具有不稳定性 .
3.三个内角相等的两个三角形不一定全等
全等基础知识和能力拓展精练
一、选择题
1.如图,AB=AC,D为BC边上一点,且BD=DC,则下列结论不正确的是( )
A. △ABD≌△ACD B. ∠ADB=90° C. ∠BAD=∠B D. AD平分∠BAC
2.如图,AB=CD,AD=CB,那么下列结论中错误的是( )
A. ∠A=∠C B. AB=AD C. AD∥BC D. AB∥CD
3.如图,点A,E,B,F在一条直线上,在△ABC和△FED中,AC=FD,BC=DE,要利用“SSS”来判定△ABC≌△FED时,下面4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE.可利用的是( )
A. ①或② B. ②或③ C. ③或① D. ①或④
4.△ABC和△DEF中,AB=2,BC=3,CA=4,DE=4,EF=3,要使△ABC与△DEF全等,则DF等于( )
A. 2 B. 3 C. 4 D. 不能确定
5.如图,在△ACE和△BDF中,AE=BF,CE=DF,要利用“SSS”证△ACE≌△BDF时,需添加一个条件是( )
A. AB=BC B. DC=BC C. AB=CD D. 以上都不对
6.如图,AB=A1B1,BC=B1C1,AC=A1C1,且∠A=110°,∠B=40°,则∠C1=( )
A. 110° B. 40° C. 30° D. 20°
7.如图,用直尺和圆规作一个角等于已知角的示意图如图所示,则说明的依据是( ).
A. B. C. D.
二、填空题
8.如图,AB=DE,AF=DC,EF=BC,∠AFB=70°,∠CDE=80°,∠ABC=_______.
9.如图,点D、E分别是△ABC的边AC、BC上的点,AD=DE,AB=BE,∠A=80°,则∠BED=____°.
10.如图,AB=ED,AC=EC,C是BD边的中点,若∠A=36°,则∠E=_________.
11.如图所示,AD=BC,AC=BD,用三角形全等的判定“边边边”可证明________≌ _______或________≌________.
12.工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C作射线OC. 由此做法得△MOC≌△NOC的依据是_______.
三、解答题
13.(2017·福建福州中考)如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.试说明:∠A=∠D.
14.如图,B、F、E、C四点在同一条直线上,AB=CD,AE=DF,CE=FB,判断∠B与∠C的关系,并证明.
15.如图所示,AC,BD相交于点O,且AB=DC,AC=DB,试判断∠A与∠D的大小关系.
16.如图,已知AB=AC,AD=AE,BD=CE,求证:∠3=∠1+∠2.
17.农科所有一块五边形的试验田如图所示,已知在五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=20 m,求这块试验田的面积.
18.如图,已知AE=DB,BC=EF,AC=DF,求证:(1)AC∥DF;(2)CB∥EF.
19.如图,已知线段AB,CD相交于点O,AD,CB的延长线交于点E,OA=OC,EA=EC.
(1)试说明:∠A=∠C;
(2)在(1)的解答过程中,需要作辅助线,它的意图是什么
参考答案
1.C
【解析】试题解析:在与中,
∴≌,
又
∴ AD平分
故选C.
2.B
【解析】∵在△ABD和△CDB中,
,
∴△ABD≌△CDB,
∴∠ADB=∠CBD,∠ABD=∠CDB,∠A=∠C
∴AD∥BC,AB∥CD,
∴A、C、D选项正确.
故选:B.
3.A
【解析】试题解析:由题意可得,要用SSS进行△ABC和△FED全等的判定,需要AB=FE,
若添加①AE=FB,则可得AE+BE=FB+BE,即AB=FE,
故①可以;
若添加AB=FE,则可直接证明两三角形的全等,故②可以,
若添加AE=BE,或BF=BE,均不能得出AB=FE,不可以利用SSS进行全等的证明,故③④不可以.
故选A.
4.A
【解析】试题解析:根据题意得: 所以如果要使与 全等,那么
故选A.
5.C
【解析】试题解析:要利用“SSS”证明≌时,需
故选C.
6.C
【解析】试题解析:∵在中,
∴≌ ,
故选C.
7.B
【解析】由作图过程可知:,,
在和中,
,
∴≌,
∴.
即能说明:的依据是“SSS”.
故选B.
8.30°
【解析】试题解析:∵CF=BE,
∴CF+EF=BE+EF,
∴CE=BF,
在△AFB和△DEC中,
∴△AFB≌△DEC(SSS),
∴在△AFB中,
故答案为:
9.80
【解析】由边边边定理可得
10.36°
【解析】试题解析:∵C是BD的中点,
∴BC=CD,
∵AB=ED,AC=EC,
∴△ABC≌△EDC(SSS),
故答案为:
11. △ADC, △BCD , △ADB, △BCA
【解析】试题解析:在△ADC和△BCD中;
∴△ADC≌△BCD(SSS).
在△ADB和△BCA中;
∴△ADB≌△BCA(SSS).
故答案为:△ADC,△BCD;△ADB,△BCA.
点睛:三条边对应相等,两个三角形全等.
12.SSS
【解析】由作图可知,OM=ON,CM=CN,OC=OC,所以△MOC≌△NOC(SSS),故答案为SSS.
13.理由见解析.
【解析】试题分析:根据题意得出BC=EF,然后结合已知条件得出△ABC和△DEF全等,从而得出答案.
试题解析:因为BE=CF,所以BE+CE=CF+CE, 所以BC=EF.
在△ABC和△DEF中, 所以△ABC≌△DEF(SSS),所以∠A=∠D.
14.∠B=∠C.
【解析】试题分析:根据已知条件证明△ABE≌△DCF,根据全等三角形的性质即可得结论.
试题解析:
结论:∠B=∠C.
理由:∵CE=BF,
∴CE+EF=EF+BF,即CF=BE,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(SSS),
∴∠B=∠C.
15.证明见解析
【解析】试题分析:连接BC.根据SSS证明≌,即可证明.
试题解析:证明:连接BC.
在和中,
∴≌(SSS),
16.证明见解析
【解析】试题分析:根据全等三角形的判定定理SSS证得对应角相等,然后通过外角的性质即可得到结论.
试题解析:证明:在△ABD与△ACE中,
∴△ABD≌△ACE,
∴∠BAD=∠1,∠ABD=∠2,
∵∠3=∠BAD+∠ABD,
∴∠3=∠1+∠2.
17.400m2.
【解析】试题分析:可延长DE至F,使EF=BC,可得△ABC≌△AEF,连AC,AD,AF,可将五边形ABCDE的面积转化为两个△ADF的面积,进而求出结论.
试题解析:如图,延长DE至点F,使EF=BC,连接AC,AD,AF.易得CD=FD.
因为
所以△ABC≌△AEF(SAS).
所以AC=AF.
在△ACD与△AFD中,因为
所以△ACD≌△AFD(SSS).
所以五边形ABCDE的面积是
2S△ADF=2×·DF·AE=2××20×20=400(m2).
18.(1)证明见解析(2)证明见解析
【解析】试题分析:(1)由SSS证明△ABC≌△DEF,得出对应角相等∠A=∠D,∠ABC=∠DEF,由内错角相等即可得出结论;
(2)由(1)得:∠ABC=∠DEF,得出∠CBE=∠FEB,由内错角相等即可得出结论.
试题解析:(1)∵AE=DB,
∴AE-BE=DB-BE,
即AB=DE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS),
∴∠A=∠D,∠ABC=∠DEF,
∴AC∥DF;
(2)由(1)得:∠ABC=∠DEF,
∴∠CBE=∠FEB,
∴CB∥EF.
19.(1)见解析;(2)构造全等三角形.
【解析】分析:(1)根据题意,没有证明两三角形全等的条件,所以要作条辅助线,连接OE;然后就可以利用SSS全等判定定理证明两三角形全等,继而∠A=∠C,本题即可证明(1),(2),说明OE的意义即可.
本题解析:
(1)如图,连接OE.
在△EAO和△ECO中,
所以△EAO≌△ECO(SSS).
所以∠A=∠C(全等三角形的对应角相等).
(2)构造全等三角形.
意图:本题运用了构造法,通过连接OE,构造△OAE,△OCE,将欲说明相等的∠A,∠C分别置于这两个三角形中,然后通过说明全等可得∠A=∠C.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
