4.3 探索三角形全等的条件(2)同步练习
文档属性
| 名称 | 4.3 探索三角形全等的条件(2)同步练习 |

|
|
| 格式 | doc | ||
| 文件大小 | 632.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-29 00:00:00 | ||
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
4.3 探索三角形全等的条件(2)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.角和它们的夹边对应相等的两个三角形全等,简写成“角边角 ”或“ASA”.
2.两角和其中一组等角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”.
基础知识和能力拓展精练
一、选择题
1.在下列条件中,不能说明△ABC≌△A’B’C’的是( )
A. ∠A=∠A’,∠C=∠C’,AC=A’C’ B. ∠A=∠A’,AB=A’B’,BC=B’C’
C. ∠B=∠B’,∠C=∠C’,AB=A’B’ D. AB=A’B’, BC=B’ C’AC=A’C’
2.如图,要测量河中礁石A离岸边B点的距 ( http: / / www.21cnjy.com )离,采取的方法如下:顺着河岸的方向任作一条线段BC,作∠CBA'=∠CBA,∠BCA'=∠BCA.可得△A'BC≌△ABC,所以A'B=AB,所以测量A'B的长即可得AB的长.判定图中两个三角形全等的理由是( )21教育网
( http: / / www.21cnjy.com )
A. SAS B. ASA C. SSS D. AAS
3.在△ABC中,AC=BC,∠ACB=9 ( http: / / www.21cnjy.com )0°,CE是过C点的一条直线,AD⊥CE于D,BE⊥CE于E,DE=4cm,AD=2cm,则BE=( )
( http: / / www.21cnjy.com )
A. 2cm B. 4cm C. 6cm或2cm D. 6cm
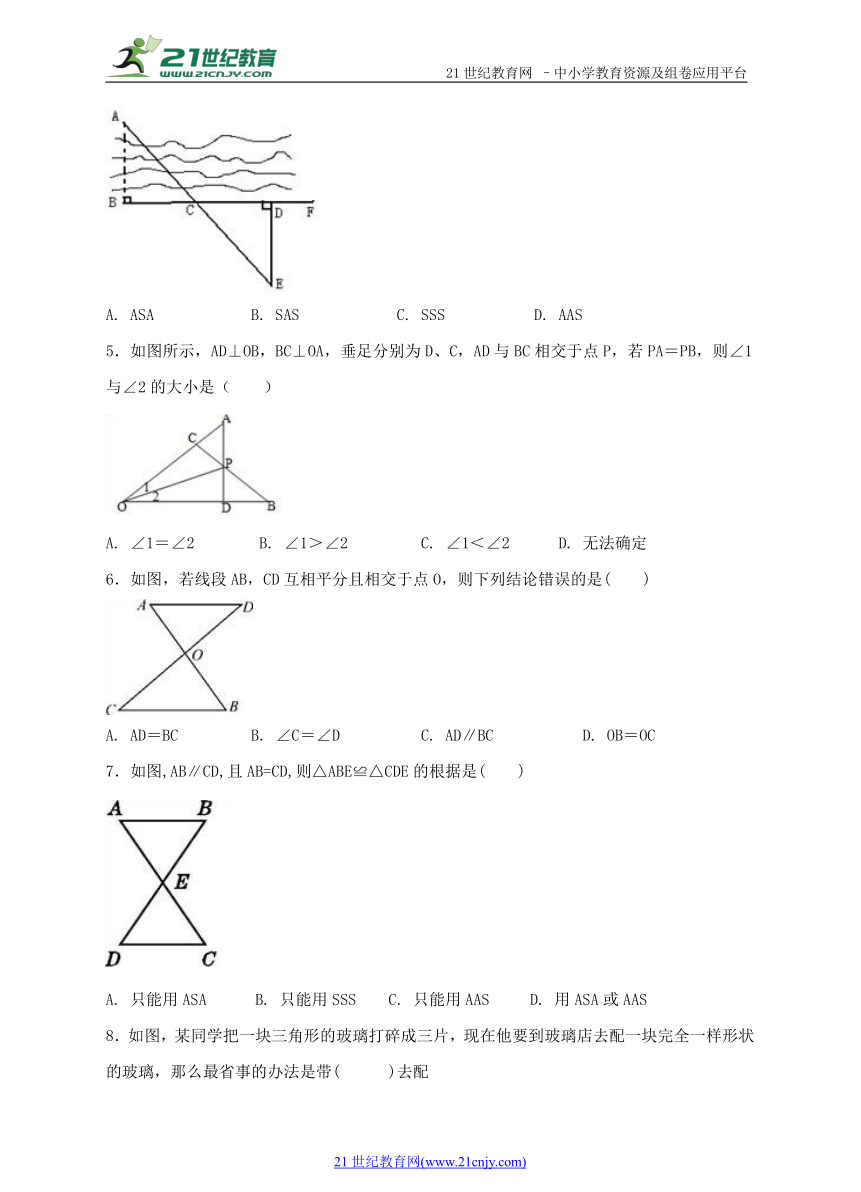
4.如图,要量河两岸相对两点A、B的距离,可以在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在一条直线上,这时可得≌,用于判定全等的最佳依据是( )【版权所有:21教育】
( http: / / www.21cnjy.com )
A. ASA B. SAS C. SSS D. AAS
5.如图所示,AD⊥OB,BC⊥OA,垂足分别为D、C,AD与BC相交于点P,若PA=PB,则∠1与∠2的大小是( )
( http: / / www.21cnjy.com )
A. ∠1=∠2 B. ∠1>∠2 C. ∠1<∠2 D. 无法确定
6.如图,若线段AB,CD互相平分且相交于点O,则下列结论错误的是( )
( http: / / www.21cnjy.com )
A. AD=BC B. ∠C=∠D C. AD∥BC D. OB=OC
7.如图,AB∥CD,且AB=CD,则△ABE≌△CDE的根据是( )
( http: / / www.21cnjy.com )
A. 只能用ASA B. 只能用SSS C. 只能用AAS D. 用ASA或AAS
8.如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块完全一样形状的玻璃,那么最省事的办法是带( )去配
( http: / / www.21cnjy.com )
A. ① B. ② C. ③ D. ①和②
二、填空题
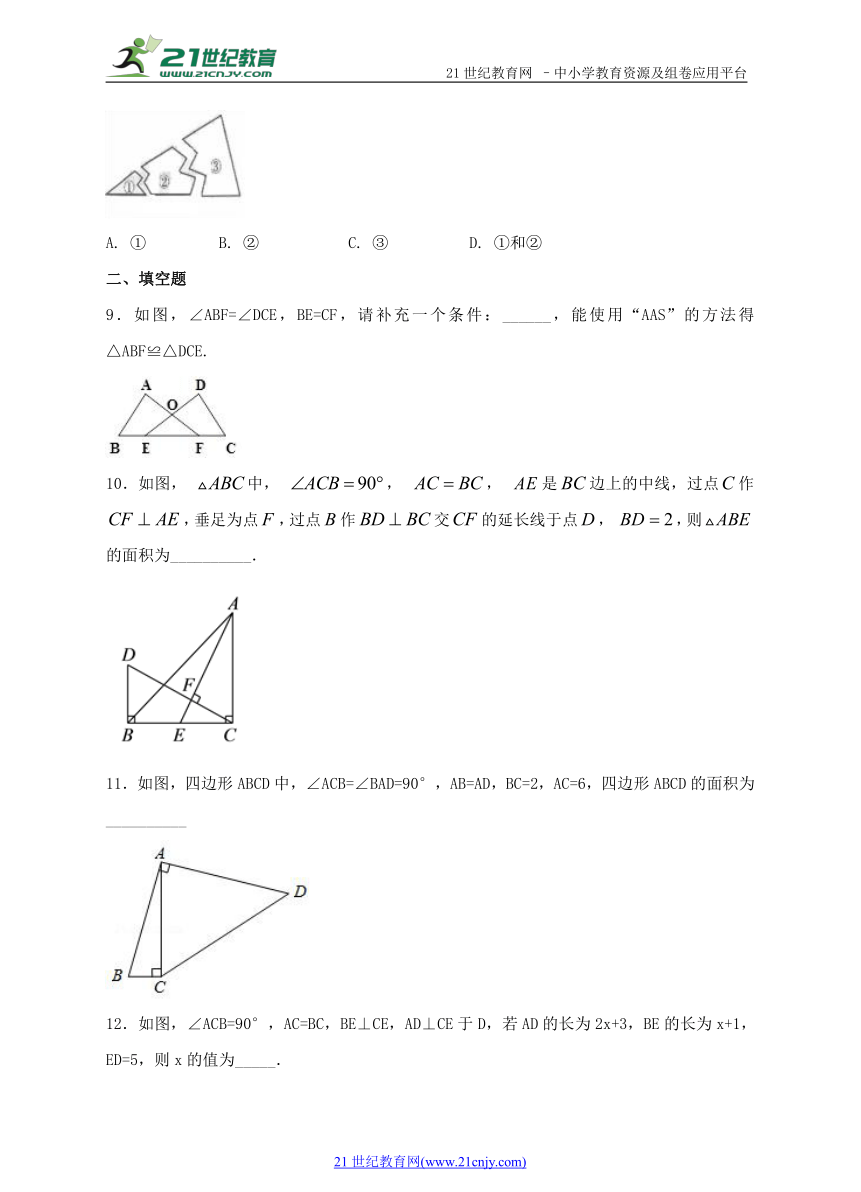
9.如图,∠ABF=∠DCE,BE=CF,请补充一个条件:______,能使用“AAS”的方法得△ABF≌△DCE.
( http: / / www.21cnjy.com )
10.如图, 中, , , 是边上的中线,过点作,垂足为点,过点作交的延长线于点, ,则的面积为__________.
( http: / / www.21cnjy.com )
11.如图,四边形ABCD中,∠ACB=∠BAD=90°,AB=AD,BC=2,AC=6,四边形ABCD的面积为__________21·cn·jy·com
( http: / / www.21cnjy.com )
12.如图,∠ACB=90°,AC=BC, ( http: / / www.21cnjy.com )BE⊥CE,AD⊥CE于D,若AD的长为2x+3,BE的长为x+1,ED=5,则x的值为_____.www.21-cn-jy.com
( http: / / www.21cnjy.com )
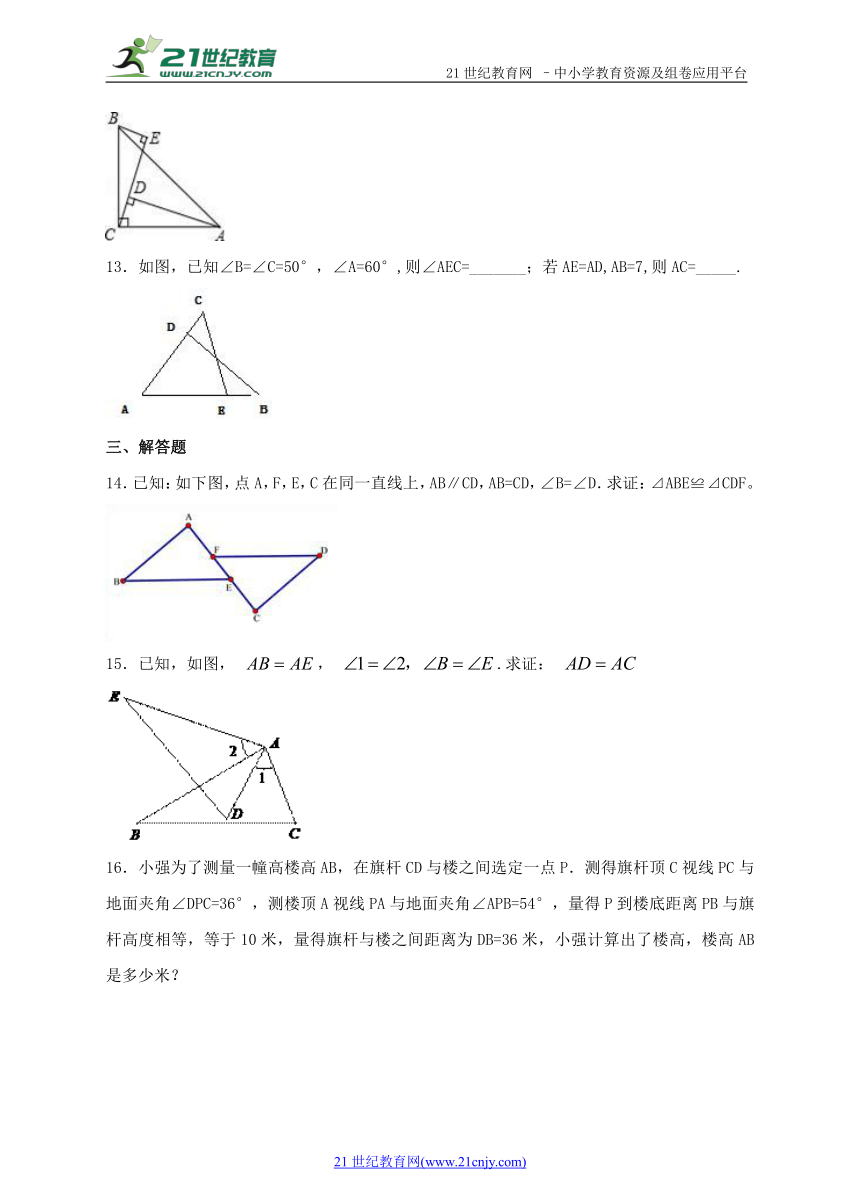
13.如图,已知∠B=∠C=50°,∠A=60°,则∠AEC=_______;若AE=AD,AB=7,则AC=_____.
( http: / / www.21cnjy.com )
三、解答题
14.已知:如下图,点A,F,E,C在同一直线上,AB∥CD,AB=CD,∠B=∠D.求证:⊿ABE≌⊿CDF。
( http: / / www.21cnjy.com )
15.已知,如图, , .求证:
( http: / / www.21cnjy.com )
16.小强为了测量一幢高楼 ( http: / / www.21cnjy.com )高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?www-2-1-cnjy-com
( http: / / www.21cnjy.com )
17.如图,在△ABC中,AD⊥BC,BE⊥AC,AD=BD,求证:BF=AC。
( http: / / www.21cnjy.com )
18. 如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.
( http: / / www.21cnjy.com )
(1)点D在边AB上时,试探究线段BD、AB和AF的数量关系,并证明你的结论;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请直接写出正确结论.
19.已知:如图所示,△ABC中,∠BAC=90°,AB=AC,分别过点B、C作经过点A的直线l的垂线段BD、CE,垂足分别D、E.21cnjy.com
(1)求证:DE=BD+CE.
(2)如果过点A的直线经过∠BAC的内部,那么上述结论还成立吗?请画出图形,直接给出你的结论(不用证明).
( http: / / www.21cnjy.com )
参考答案
1.B
【解析】A、∠A=∠A′,∠C=∠C′,AC=A′C′,可用ASA判定△ABC≌△A′B′C,故选项正确;21*cnjy*com
B、∠A=∠A′,AB=A′B′,BC=B′C′,SSA不能判定两个三角形全等,故选项错误;
C、∠B=∠B′,∠C=∠C′,AB=A′B′,可用AAS判定△ABC≌△A′B′C,故选项正确;
D、AB=A′B′,BC=B′C,AC=A′C′,可用ASA判定△ABC≌△A′B′C,故选项正确.
故选:B.
2.B
【解析】试题解析:在△△A'BC和△ABC中,
∵
∴△A'BC≌△ABC(ASA)
∴A'B=AB.
故选B.
3.C
【解析】试题解析:分为两种情况:
①如图1,当CE在△ABC内.
( http: / / www.21cnjy.com )
∵AD⊥CE,∠BCA=90°,
∴∠ADC=∠BCA=90°,
∴∠DCA+∠BCE=90°,∠DCA+∠DAC=90°,
∴∠DAC=∠BCE,
∵AD⊥CE,BE⊥CE,
∴∠ADC=∠BEC=90°,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS)
∴CE=AD=2cm,CD=BE,
BE=CD=CE+DE=2cm+4cm=6cm;
②如图2,当CE在△ABC外.
( http: / / www.21cnjy.com )
∵在△EBC和△DAC中,
,
∴△ACD≌△CBE(AAS),
∴CE=AD=2cm,BE=CD,
∴BE=CD=DE﹣AD=4cm﹣2cm=2cm,
故答案为:6或2.
故选C.
4.A
【解析】在△ABC和△EDC中, ,∴△ABC≌△ EDC(ASA);故选A.
5.A
【解析】∵AD⊥OB,BC⊥OA,垂足分别为D、C,AD与BC相交于点P,PA=PB,∠CPA=∠DPB,
∴△CPA≌△∠DPB(AAS),
∴PC=PD,
∴∠1=∠2,
故选A.
点睛:本题考查了三角形全等的判定和性质 ( http: / / www.21cnjy.com );主要先利用全等三角形证明CP=DP,再由角平分线的逆定理可知OP是角AOB的平分线,由判定可知∠1=∠2. 2-1-c-n-j-y
6.D
【解析】∵AB、CD互相平分,
∴AO=BO,CO=DO,
在△AOD和△BOC中,
AO=BO,
∠AOD=∠BOC,
CO=DO ,
∴△AOD≌△BOC(SAS),
∴AD=BC,故A选项正确;
∠C=∠D,故B选项正确;
∴AD∥BC,故C选项正确;
OB与OC不是对应边,不一定相等,故D选项错误。
故选D.
点睛:本题考查了全等三角形的判定和性质,在证明三角形全等时,注意隐含条件的应用,如“公共边”、“公共角”、“对顶角相等”.21世纪教育网版权所有
7.D
【解析】解:∵AB∥CD,∴∠A=∠C,∠B=∠D.
又∵∠AEB=∠CED(对顶角相等),AB=CD,∴可用ASA或AAS进行△ABE≌△CDE的判定.故选D.21*cnjy*com
8.C
【解析】第③块玻璃有完整的两角及其所夹边,我们可以根据角边角定理配出另一块玻璃与之全等.
故选C.
点睛:掌握三角形全等的判定方法.
9.∠A=∠D
【解析】∵BE=CF,
∴BE+EF=CF+EF,即BF=CE,
又∵∠ABF=∠DCE,
∴要使用“AAS”证明△ABF≌△DCE.,需添加条件:∠A=∠D.
故答案为:∠A=∠D.
10.4
【解析】∵, , ,
∴,
∵, ,
∴,
∴≌.
∴,
∵, ,
∴.
( http: / / www.21cnjy.com )
故答案为4.
11.24
【解析】作EA⊥AC,DE⊥AE,
( http: / / www.21cnjy.com )
∵∠BAC+∠CAD=90°,∠EAD+∠CAD=90°,
∴∠BAC=∠EAD,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(AAS),
∴AE=AC,
∴四边形ABCD的面积=四边形ACDE的面积,
∵四边形ACDE的面积= (AC+DE)AE=×8×6=24,
∴四边形ABCD的面积=24,
故答案为24.
12.3
【解析】解:∵BE⊥CE,AD⊥CE,
∴∠BCE+∠ACD=90°,∠CAD+∠ACD=90°,
∴∠BCE=∠CAD,
在△BCE与△CAD中
∵AC=BC,
∠BEC=∠CDA,
∠BCE=∠ACD,,
∴△BCE≌△CAD,
∴BE=CD,AD=CE,
又∵AD的长为2x+3,BE的长为x+1,ED=5,
∴CD+DE=CE=AD,即可得出方程x+1+5=2x+3,
解得:x=3.
点睛:首先判断出∠BCE=∠ACD ( http: / / www.21cnjy.com ),再结合AC=BC,∠BEC=∠CDA=90°,可判断△BCE≌△CAD,得出BE=CD,AD=CE,从而根据CD+DE=CE=AD,得出方程x+1+5=2x+3,解出即可得出x的值.
13. 70° 7
【解析】△AEC中,∠AEC=180°-∠A-∠C=180°-60°-50°=70°;
因为∠B=∠C,∠A=∠A,AE=AD,所以△ABD≌△ACE,所以AC=AB=7.
故答案为 (1). 70°;(2). 7.
14.证明见解析.
【解析】试题分析:由AB∥CD可得∠A=∠C,根据ASA可证得△ABE≌△CDF.
试题解析:
证明:∵AB∥DC,
∴∠A=∠C
在⊿ABE和⊿CDF中,
∴△ABE≌△CDF(ASA)
15.证明见解析.
【解析】试题分析:首先根据∠1=∠2可证明,然后可以证明,即可证明.
试题解析:∵,
∴,
即,
在和中, ,
∴,
∴.
16.楼高AB是26米.
【解析】试题分析: 因为∠CPD=36°,∠APB=54°,∠CDP=∠ABP=90°,
所以∠DCP=∠APB=54°,根据, , 判定△CPD≌△PAB,根据全等三角形的性质进而得出AB的长.2·1·c·n·j·y
试题解析:∵∠CPD=36°,∠APB=54°,∠CDP=∠ABP=90°,
∴∠DCP=∠APB=54°,
在△CPD和△PAB中,
∵,
∴△CPD≌△PAB(ASA),
∴DP=AB,
∵DB=36,PB=10,
∴AB=36﹣10=26(m),
答:楼高AB是26米.
17.证明见解析
【解析】分析:先证出∠DBF=∠DAC,再由ASA证明△BDF≌△ADC,得出对应边相等即可.
本题解析:
∵AD⊥BC,BE⊥AC,
∴∠BDF=∠ADC=∠BEC=90°,
∴∠DBF+∠C=90°,∠DAC+∠C=90°,
∴∠DBF=∠DAC,
在△BDF和△ADC中,
∴△BDF≌△ADC(ASA),
∴BF=AC。
点睛:本题考查了全等三角形的判定与性质;熟练掌握三角形全等的方法,找到三角形全等的条件是解决问题的关键.21·世纪*教育网
18.(1)见解析;(2)见解析
【解析】 试题分析:(1)通过三角形全等的判定ASA证明△FAB≌△DAC,然后根据全等三角形的性质可证得结论;【出处:21教育名师】
(2)根据题意,分为:点D在AB的延长线上;点D在AB的反向延长线上,两种情况进行讨论即可.
试题解析:(1)如图1,
( http: / / www.21cnjy.com )
∵BE⊥CD即∠BEC=90°,∠BAC=90°,
∴∠F+∠FBA=90°,∠F+∠FCE=90°.
∴∠FBA=∠FCE.
∵∠FAB=180°-∠DAC=90°,
∴∠FAB=∠DAC.
在△FAB和△DAC中,
( http: / / www.21cnjy.com )
AB=AC
( http: / / www.21cnjy.com )
∴△FAB≌△DAC(ASA).
∴FA=DA.
∴AB=AD+BD=FA+BD.
(2)(1)中的结论不成立.
点D在AB的延长线上时,AB=AF-BD;点D在AB的反向延长线上时,AB=BD-AF.
理由如下:
①当点D在AB的延长线上时,如图2.
( http: / / www.21cnjy.com )
同理可得:FA=DA.
则AB=AD-BD=AF-BD.
②点D在AB的反向延长线上时,如图3.
( http: / / www.21cnjy.com )
同理可得:FA=DA.
则AB=BD-AD=BD-AF.
19.(1)见解析;(2)上述结论不成立.
【解析】试题分析:(1)由垂线的定义和角的互余关系得出 由AAS证明≌,得出对应边相等 由 即可得出结论;
(2)由垂线的定义和角的互余关系得出 由AAS证明≌,得出对应边相等由 之间的和差关系,即可得出结论.【来源:21·世纪·教育·网】
试题解析:(1)∵∠BAC=,
∴∠BAD+∠CAE=,
∵BD⊥l,CE⊥l,
∴∠ADB=∠CEA=,
∴∠BAD+∠ABD=,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AD+AE=DE,
∴BD+CE=DE;
(2)上述结论不成立,
如图所示,BD=DE+CE.
( http: / / www.21cnjy.com )
证明:∵∠BAC=,
∴∠BAD+∠CAE=,
∵BD⊥l,CE⊥l,
∴∠ADB=∠CEA=,
∴∠BAD+∠ABD=,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AD+DE=AE,
∴BD=DE+CE.
如图所示,CE=DE+BD,
( http: / / www.21cnjy.com )
证明:证明:∵∠BAC=,
∴∠BAD+∠CAE=,
∵BD⊥l,CE⊥l,
∴∠ADB=∠CEA=,
∴∠BAD+∠ABD=,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AE+DE=AD,
∴CE=DE+BD.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.3 探索三角形全等的条件(2)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.角和它们的夹边对应相等的两个三角形全等,简写成“角边角 ”或“ASA”.
2.两角和其中一组等角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”.
基础知识和能力拓展精练
一、选择题
1.在下列条件中,不能说明△ABC≌△A’B’C’的是( )
A. ∠A=∠A’,∠C=∠C’,AC=A’C’ B. ∠A=∠A’,AB=A’B’,BC=B’C’
C. ∠B=∠B’,∠C=∠C’,AB=A’B’ D. AB=A’B’, BC=B’ C’AC=A’C’
2.如图,要测量河中礁石A离岸边B点的距 ( http: / / www.21cnjy.com )离,采取的方法如下:顺着河岸的方向任作一条线段BC,作∠CBA'=∠CBA,∠BCA'=∠BCA.可得△A'BC≌△ABC,所以A'B=AB,所以测量A'B的长即可得AB的长.判定图中两个三角形全等的理由是( )21教育网
( http: / / www.21cnjy.com )
A. SAS B. ASA C. SSS D. AAS
3.在△ABC中,AC=BC,∠ACB=9 ( http: / / www.21cnjy.com )0°,CE是过C点的一条直线,AD⊥CE于D,BE⊥CE于E,DE=4cm,AD=2cm,则BE=( )
( http: / / www.21cnjy.com )
A. 2cm B. 4cm C. 6cm或2cm D. 6cm
4.如图,要量河两岸相对两点A、B的距离,可以在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在一条直线上,这时可得≌,用于判定全等的最佳依据是( )【版权所有:21教育】
( http: / / www.21cnjy.com )
A. ASA B. SAS C. SSS D. AAS
5.如图所示,AD⊥OB,BC⊥OA,垂足分别为D、C,AD与BC相交于点P,若PA=PB,则∠1与∠2的大小是( )
( http: / / www.21cnjy.com )
A. ∠1=∠2 B. ∠1>∠2 C. ∠1<∠2 D. 无法确定
6.如图,若线段AB,CD互相平分且相交于点O,则下列结论错误的是( )
( http: / / www.21cnjy.com )
A. AD=BC B. ∠C=∠D C. AD∥BC D. OB=OC
7.如图,AB∥CD,且AB=CD,则△ABE≌△CDE的根据是( )
( http: / / www.21cnjy.com )
A. 只能用ASA B. 只能用SSS C. 只能用AAS D. 用ASA或AAS
8.如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块完全一样形状的玻璃,那么最省事的办法是带( )去配
( http: / / www.21cnjy.com )
A. ① B. ② C. ③ D. ①和②
二、填空题
9.如图,∠ABF=∠DCE,BE=CF,请补充一个条件:______,能使用“AAS”的方法得△ABF≌△DCE.
( http: / / www.21cnjy.com )
10.如图, 中, , , 是边上的中线,过点作,垂足为点,过点作交的延长线于点, ,则的面积为__________.
( http: / / www.21cnjy.com )
11.如图,四边形ABCD中,∠ACB=∠BAD=90°,AB=AD,BC=2,AC=6,四边形ABCD的面积为__________21·cn·jy·com
( http: / / www.21cnjy.com )
12.如图,∠ACB=90°,AC=BC, ( http: / / www.21cnjy.com )BE⊥CE,AD⊥CE于D,若AD的长为2x+3,BE的长为x+1,ED=5,则x的值为_____.www.21-cn-jy.com
( http: / / www.21cnjy.com )
13.如图,已知∠B=∠C=50°,∠A=60°,则∠AEC=_______;若AE=AD,AB=7,则AC=_____.
( http: / / www.21cnjy.com )
三、解答题
14.已知:如下图,点A,F,E,C在同一直线上,AB∥CD,AB=CD,∠B=∠D.求证:⊿ABE≌⊿CDF。
( http: / / www.21cnjy.com )
15.已知,如图, , .求证:
( http: / / www.21cnjy.com )
16.小强为了测量一幢高楼 ( http: / / www.21cnjy.com )高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?www-2-1-cnjy-com
( http: / / www.21cnjy.com )
17.如图,在△ABC中,AD⊥BC,BE⊥AC,AD=BD,求证:BF=AC。
( http: / / www.21cnjy.com )
18. 如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.
( http: / / www.21cnjy.com )
(1)点D在边AB上时,试探究线段BD、AB和AF的数量关系,并证明你的结论;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请直接写出正确结论.
19.已知:如图所示,△ABC中,∠BAC=90°,AB=AC,分别过点B、C作经过点A的直线l的垂线段BD、CE,垂足分别D、E.21cnjy.com
(1)求证:DE=BD+CE.
(2)如果过点A的直线经过∠BAC的内部,那么上述结论还成立吗?请画出图形,直接给出你的结论(不用证明).
( http: / / www.21cnjy.com )
参考答案
1.B
【解析】A、∠A=∠A′,∠C=∠C′,AC=A′C′,可用ASA判定△ABC≌△A′B′C,故选项正确;21*cnjy*com
B、∠A=∠A′,AB=A′B′,BC=B′C′,SSA不能判定两个三角形全等,故选项错误;
C、∠B=∠B′,∠C=∠C′,AB=A′B′,可用AAS判定△ABC≌△A′B′C,故选项正确;
D、AB=A′B′,BC=B′C,AC=A′C′,可用ASA判定△ABC≌△A′B′C,故选项正确.
故选:B.
2.B
【解析】试题解析:在△△A'BC和△ABC中,
∵
∴△A'BC≌△ABC(ASA)
∴A'B=AB.
故选B.
3.C
【解析】试题解析:分为两种情况:
①如图1,当CE在△ABC内.
( http: / / www.21cnjy.com )
∵AD⊥CE,∠BCA=90°,
∴∠ADC=∠BCA=90°,
∴∠DCA+∠BCE=90°,∠DCA+∠DAC=90°,
∴∠DAC=∠BCE,
∵AD⊥CE,BE⊥CE,
∴∠ADC=∠BEC=90°,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS)
∴CE=AD=2cm,CD=BE,
BE=CD=CE+DE=2cm+4cm=6cm;
②如图2,当CE在△ABC外.
( http: / / www.21cnjy.com )
∵在△EBC和△DAC中,
,
∴△ACD≌△CBE(AAS),
∴CE=AD=2cm,BE=CD,
∴BE=CD=DE﹣AD=4cm﹣2cm=2cm,
故答案为:6或2.
故选C.
4.A
【解析】在△ABC和△EDC中, ,∴△ABC≌△ EDC(ASA);故选A.
5.A
【解析】∵AD⊥OB,BC⊥OA,垂足分别为D、C,AD与BC相交于点P,PA=PB,∠CPA=∠DPB,
∴△CPA≌△∠DPB(AAS),
∴PC=PD,
∴∠1=∠2,
故选A.
点睛:本题考查了三角形全等的判定和性质 ( http: / / www.21cnjy.com );主要先利用全等三角形证明CP=DP,再由角平分线的逆定理可知OP是角AOB的平分线,由判定可知∠1=∠2. 2-1-c-n-j-y
6.D
【解析】∵AB、CD互相平分,
∴AO=BO,CO=DO,
在△AOD和△BOC中,
AO=BO,
∠AOD=∠BOC,
CO=DO ,
∴△AOD≌△BOC(SAS),
∴AD=BC,故A选项正确;
∠C=∠D,故B选项正确;
∴AD∥BC,故C选项正确;
OB与OC不是对应边,不一定相等,故D选项错误。
故选D.
点睛:本题考查了全等三角形的判定和性质,在证明三角形全等时,注意隐含条件的应用,如“公共边”、“公共角”、“对顶角相等”.21世纪教育网版权所有
7.D
【解析】解:∵AB∥CD,∴∠A=∠C,∠B=∠D.
又∵∠AEB=∠CED(对顶角相等),AB=CD,∴可用ASA或AAS进行△ABE≌△CDE的判定.故选D.21*cnjy*com
8.C
【解析】第③块玻璃有完整的两角及其所夹边,我们可以根据角边角定理配出另一块玻璃与之全等.
故选C.
点睛:掌握三角形全等的判定方法.
9.∠A=∠D
【解析】∵BE=CF,
∴BE+EF=CF+EF,即BF=CE,
又∵∠ABF=∠DCE,
∴要使用“AAS”证明△ABF≌△DCE.,需添加条件:∠A=∠D.
故答案为:∠A=∠D.
10.4
【解析】∵, , ,
∴,
∵, ,
∴,
∴≌.
∴,
∵, ,
∴.
( http: / / www.21cnjy.com )
故答案为4.
11.24
【解析】作EA⊥AC,DE⊥AE,
( http: / / www.21cnjy.com )
∵∠BAC+∠CAD=90°,∠EAD+∠CAD=90°,
∴∠BAC=∠EAD,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(AAS),
∴AE=AC,
∴四边形ABCD的面积=四边形ACDE的面积,
∵四边形ACDE的面积= (AC+DE)AE=×8×6=24,
∴四边形ABCD的面积=24,
故答案为24.
12.3
【解析】解:∵BE⊥CE,AD⊥CE,
∴∠BCE+∠ACD=90°,∠CAD+∠ACD=90°,
∴∠BCE=∠CAD,
在△BCE与△CAD中
∵AC=BC,
∠BEC=∠CDA,
∠BCE=∠ACD,,
∴△BCE≌△CAD,
∴BE=CD,AD=CE,
又∵AD的长为2x+3,BE的长为x+1,ED=5,
∴CD+DE=CE=AD,即可得出方程x+1+5=2x+3,
解得:x=3.
点睛:首先判断出∠BCE=∠ACD ( http: / / www.21cnjy.com ),再结合AC=BC,∠BEC=∠CDA=90°,可判断△BCE≌△CAD,得出BE=CD,AD=CE,从而根据CD+DE=CE=AD,得出方程x+1+5=2x+3,解出即可得出x的值.
13. 70° 7
【解析】△AEC中,∠AEC=180°-∠A-∠C=180°-60°-50°=70°;
因为∠B=∠C,∠A=∠A,AE=AD,所以△ABD≌△ACE,所以AC=AB=7.
故答案为 (1). 70°;(2). 7.
14.证明见解析.
【解析】试题分析:由AB∥CD可得∠A=∠C,根据ASA可证得△ABE≌△CDF.
试题解析:
证明:∵AB∥DC,
∴∠A=∠C
在⊿ABE和⊿CDF中,
∴△ABE≌△CDF(ASA)
15.证明见解析.
【解析】试题分析:首先根据∠1=∠2可证明,然后可以证明,即可证明.
试题解析:∵,
∴,
即,
在和中, ,
∴,
∴.
16.楼高AB是26米.
【解析】试题分析: 因为∠CPD=36°,∠APB=54°,∠CDP=∠ABP=90°,
所以∠DCP=∠APB=54°,根据, , 判定△CPD≌△PAB,根据全等三角形的性质进而得出AB的长.2·1·c·n·j·y
试题解析:∵∠CPD=36°,∠APB=54°,∠CDP=∠ABP=90°,
∴∠DCP=∠APB=54°,
在△CPD和△PAB中,
∵,
∴△CPD≌△PAB(ASA),
∴DP=AB,
∵DB=36,PB=10,
∴AB=36﹣10=26(m),
答:楼高AB是26米.
17.证明见解析
【解析】分析:先证出∠DBF=∠DAC,再由ASA证明△BDF≌△ADC,得出对应边相等即可.
本题解析:
∵AD⊥BC,BE⊥AC,
∴∠BDF=∠ADC=∠BEC=90°,
∴∠DBF+∠C=90°,∠DAC+∠C=90°,
∴∠DBF=∠DAC,
在△BDF和△ADC中,
∴△BDF≌△ADC(ASA),
∴BF=AC。
点睛:本题考查了全等三角形的判定与性质;熟练掌握三角形全等的方法,找到三角形全等的条件是解决问题的关键.21·世纪*教育网
18.(1)见解析;(2)见解析
【解析】 试题分析:(1)通过三角形全等的判定ASA证明△FAB≌△DAC,然后根据全等三角形的性质可证得结论;【出处:21教育名师】
(2)根据题意,分为:点D在AB的延长线上;点D在AB的反向延长线上,两种情况进行讨论即可.
试题解析:(1)如图1,
( http: / / www.21cnjy.com )
∵BE⊥CD即∠BEC=90°,∠BAC=90°,
∴∠F+∠FBA=90°,∠F+∠FCE=90°.
∴∠FBA=∠FCE.
∵∠FAB=180°-∠DAC=90°,
∴∠FAB=∠DAC.
在△FAB和△DAC中,
( http: / / www.21cnjy.com )
AB=AC
( http: / / www.21cnjy.com )
∴△FAB≌△DAC(ASA).
∴FA=DA.
∴AB=AD+BD=FA+BD.
(2)(1)中的结论不成立.
点D在AB的延长线上时,AB=AF-BD;点D在AB的反向延长线上时,AB=BD-AF.
理由如下:
①当点D在AB的延长线上时,如图2.
( http: / / www.21cnjy.com )
同理可得:FA=DA.
则AB=AD-BD=AF-BD.
②点D在AB的反向延长线上时,如图3.
( http: / / www.21cnjy.com )
同理可得:FA=DA.
则AB=BD-AD=BD-AF.
19.(1)见解析;(2)上述结论不成立.
【解析】试题分析:(1)由垂线的定义和角的互余关系得出 由AAS证明≌,得出对应边相等 由 即可得出结论;
(2)由垂线的定义和角的互余关系得出 由AAS证明≌,得出对应边相等由 之间的和差关系,即可得出结论.【来源:21·世纪·教育·网】
试题解析:(1)∵∠BAC=,
∴∠BAD+∠CAE=,
∵BD⊥l,CE⊥l,
∴∠ADB=∠CEA=,
∴∠BAD+∠ABD=,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AD+AE=DE,
∴BD+CE=DE;
(2)上述结论不成立,
如图所示,BD=DE+CE.
( http: / / www.21cnjy.com )
证明:∵∠BAC=,
∴∠BAD+∠CAE=,
∵BD⊥l,CE⊥l,
∴∠ADB=∠CEA=,
∴∠BAD+∠ABD=,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AD+DE=AE,
∴BD=DE+CE.
如图所示,CE=DE+BD,
( http: / / www.21cnjy.com )
证明:证明:∵∠BAC=,
∴∠BAD+∠CAE=,
∵BD⊥l,CE⊥l,
∴∠ADB=∠CEA=,
∴∠BAD+∠ABD=,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AE+DE=AD,
∴CE=DE+BD.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
