4.5 利用三角形全等测距离同步练习
文档属性
| 名称 | 4.5 利用三角形全等测距离同步练习 |  | |
| 格式 | docx | ||
| 文件大小 | 503.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-29 17:17:07 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
4.5 利用三角形全等测距离同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.利用三角形全等测距离,实际是构建全等三角形,运用全等三角形的对应边相等,把较难测量和无法测量的距离转化成已知线段或较容易测量的线段的长度,从而得到被测距离.
2.数学方法:转化法,即把难以测量或无法测量的线段(或角)转化为易测量的线段(或角).
3. 步骤:①明确实际问题应该用哪些几何知识解决;②根据实际问题抽象出几何图形;③结合图形和题意分析已知条件;④找对解决问题的途径.
基础知识和能力拓展精练
一、选择题
1.利用三角形全等测量距离的原理是( )
A. 全等三角形对应角相等 B. 全等三角形对应边相等
C. 大小和形状相同的两个三角形全等 D. 三边对应相等的两个三角形全等
2.工人师傅常用角尺平分任意角,做法如下:如图,∠AOB是一个任意角,在OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点P的射线OP便是∠AOB的平分线,师傅这么做的依据是( )
A. SAS B. SSS C. 角平分线逆定理 D. AAS
3.如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,如图所示的这种方法,是利用了三角形全等中的( )
A. SSS B. ASA C. AAS D. SAS
4.某大学计划为新生配备如图①所示的折叠凳.图②是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30 cm,则由以上信息可推得CB的长度也为30 cm,依据是( )
A. SAS B. ASA C. SSS D. AAS
5.如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( )
A. SAS B. ASA C. AAS D. SSS
6.如图所示,已知BO=OC,AO=DO,CD=100m,则A,B两点间的距离( )
A. 大于100m B. 等于100m C. 小于100m D. 无法确定
7.如图,要测量河中礁石A离岸边B点的距离,采取的方法如下:顺着河岸的方向任作一条线段BC,作∠CBA'=∠CBA,∠BCA'=∠BCA.可得△A'BC≌△ABC,所以A'B=AB,所以测量A'B的长即可得AB的长.判定图中两个三角形全等的理由是( )
A. SAS B. ASA C. SSS D. AAS
8.如图,AA',BB'表示两根长度相同的木条,若O是AA',BB'的中点,经测量AB=9 cm,则容器的内径A'B'为( )
A. 8 cm B. 9 cm C. 10 cm D. 11 cm
二、填空题
9.如图,有一池塘,要测池塘两端A、B两点的距离,可先在平地上取一个可以直接到达A、B两点的C,连接AC并延长AC到点D,使CD=CA,连结BC并延长BC到点E,使CE=CB,连接DE,那么量出________的长就等于AB的长. 这是因为可根据________方法判定△ABC≌△DEC.
10.“三月三,放风筝”,如图是小明制作的风筝,他根据DE=DF,EH=FH,不用度量,就知道∠DEH=∠DFH,小明是通过全等三角形的识别得到的结论,请问小明用的识别方法是_____(用字母表示).
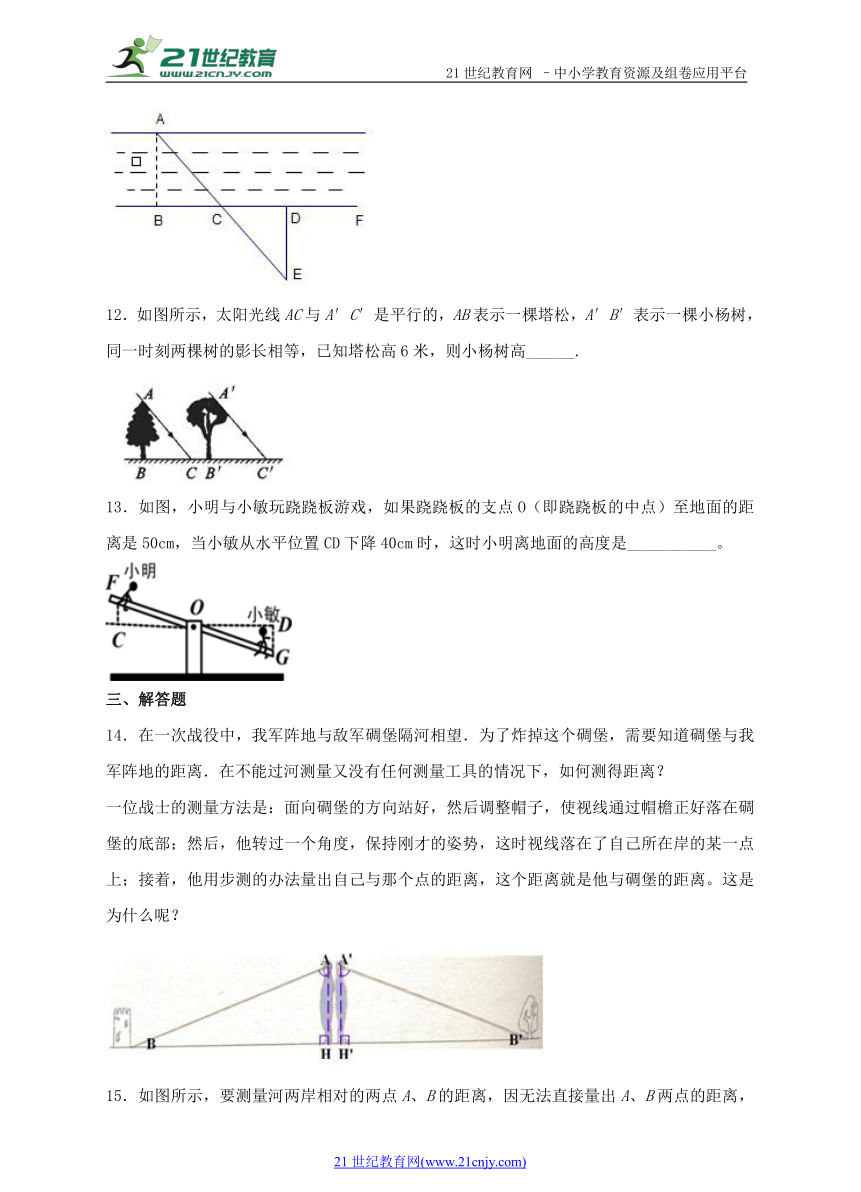
11.如图所示,要测量河宽AB的长,在AB的垂线BF上选取两点C,D,使CD=BC,再作DE⊥BF交BF于点D,且使A,C,E在同一条直线上,这时测得DE的长为30m,则河宽为______m.
12.如图所示,太阳光线AC与A′C′是平行的,AB表示一棵塔松,A′B′表示一棵小杨树,同一时刻两棵树的影长相等,已知塔松高6米,则小杨树高______.
13.如图,小明与小敏玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50cm,当小敏从水平位置CD下降40cm时,这时小明离地面的高度是___________。
三、解答题
14.在一次战役中,我军阵地与敌军碉堡隔河相望.为了炸掉这个碉堡,需要知道碉堡与我军阵地的距离.在不能过河测量又没有任何测量工具的情况下,如何测得距离?
一位战士的测量方法是:面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离。这是为什么呢?
15.如图所示,要测量河两岸相对的两点A、B的距离,因无法直接量出A、B两点的距离,请你设计一种方案,求出A、B的距离,并说明理由.
16.如图,房间内有一架梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为a米,此时梯子的倾斜角为75°,若梯子斜靠在另一面墙时,顶端距地面的垂直距离NB为b米,梯子的倾斜角为45°,则这个房间的宽AB是多少米?为什么?
17.如图,一艘轮船沿AC方向航行,轮船在点A时测得航线两侧的两个灯塔D、E与航线的夹角相等,当轮船到达点B时测得这两个灯塔与航线的夹角仍然相等,这时轮船与两个灯塔的距离是否相等?为什么?
18.在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,
(1)求高台A比矮台B高多少米?
(2)求旗杆的高度OM;
19.如图所示的A、B是两根呈南北方向排列的电线杆,A、B之间有一条小河,小刚想估测这两根电线杆之间的距离,于是小刚从A点开始向正西方向走了20步到达一棵大树C处,接着又向前走了20步到达D处,然后他左转90°直行,当他看到电线杆B、大树C和他自己现在所处的位置E恰在同一条直线上时,他从D位置走到E处恰好走了100步,利用上述数据,小刚测出了A、B两根电线杆之间的距离.
(1)请你根据上述的测量方法在原图上画出示意图;
(2)如果小刚一步大约60厘米,请你求A、B两根电线杆之间的距离并简述理由.
参考答案
1.B
【解析】利用三角形全等测量距离,是指无法直接测量时,我们通过构造全等的方法,然后借助全等三角形对应边相等,间接测量距离,故选B.
2.B
【解析】∵OM=ON,PM=PN,OP为公共边,
∴△MOP≌△NOP(SSS).
故选B.
3.D
【解析】由原题可得:
AC = DC
∠ACB=∠DCB
BC =BC
∴△ACB ≌△DCB(SAS)
∴AB = DB
故选D。
4.A
【解析】试题解析:∵O是AB、CD的中点,
∴OA=OB,OC=OD,
在△AOD和△BOC中,
,
∴△AOD≌△BOC(SAS),
∴CB=AD,
∵AD=30cm,
∴CB=30cm.
故选A.
5.A
【解析】在△COD和△AOB中, ,
∴△COD≌△AOB(SAS),
故选A.
6.B
【解析】∵AC=DB,AO=DO,
∴OB=OC,
又∠AOB=∠DOC,
∴△AOB≌△DOC,
∴AB=CD=100m.
故选B.
7.B
【解析】试题解析:在△△A'BC和△ABC中,
∵
∴△A'BC≌△ABC(ASA)
∴A'B=AB.
故选B.
8.B
【解析】解:由题意知:OA=OA′,∠AOB=∠A′OB′,OB=OB′,∴△AOB≌△A′OB′,∴A′B′=AB=9cm.故选B.
点睛:本题考查了全等三角形的判定及性质的应用;解答本题的关键是设计三角形全等,巧妙地借助两个三角形全等,寻找所求线段与已知线段之间的等量关系.
9. ED SAS
【解析】解:量出DE的长就等于AB的长.这是因为可根据SAS方法判定△ABC≌△DEC.故答案为:DE,SAS.
点睛:本题考查了全等三角形的应用,熟练掌握三角形全等的判定方法是解题的关键.
10.SSS
【解析】因为DE=DF,EH=FH,DH=DH,利用SSS可判定△DEH=△DFH,所以∠DEH=∠DFH,故答案为:SSS.
11.30
【解析】因为AB⊥BF,DE⊥BF,所以∠ABC=∠EDC=90°;
因为CD=BC,对顶角∠ACB=∠ECD,所以△ABC≌△EDC;
所以AB=DE=30,
故答案为:30.
点睛:本题考查全等三角形判定定理,有两角和其中一角的对边对应相等的两个三角形全等.注意隐含条件,对顶角相等.
12.6米
【解析】试题解析:∵ AC∥A′C′
∴∠ACB=∠A′C′B′(两直线平行,同位角相等)
∵ 树木是垂直地面生长的,
∴∠ABC=∠A′B′C′=90°,
∵∠ABC=∠A′B′C′,∠ACB=∠A′C′B′,AC∥A′C′,
∴△ABC≌△A′B′C′(两角及其夹边对应相等的两个三角形全等),
∴AB=A′B′=6米 (全等三角形的对应边相等),
所以小杨树的高为6米.
故答案为:6米.
13.90cm
【解析】试题解析:∵O是CD和FG的中点,
∴FO=OG,CO=DO,
又∠FOC=∠GOD,
∴ΔFOC≌ΔGOD,
∴FC=GD=40cm,
∴小明离地面的高度是:50+40=90cm.
14.见解析
【解析】分析:根据三角形全等的判定方法,得到一些相应线段或角相等,在现实生活中有许多应用的实例.
本题解析:
在本题中,根据题意可以知道,满足了三个条件:
(1)身体高度一定,(2)帽檐处的角度一定,(3)脚下的直角一定,
故根据ASA判定方法,可以得到两个三角形全全等,
∴距离相等。
理由是:在△AHB与中,
∴
点睛:本题主要考查作图—应用与设计作图,根据题意画出示意图,并熟练掌握全等三角形的判定与性质是解题的关键.
15.见解析
【解析】分析:根据题中垂直可得到一组角相等,再根据对顶角相等,已知一组边相等,得到三角形全等的三个条件,于是根据ASA可得到三角形全等,全等三角形的对应边相等,得结论.
本题解析:
在AB的垂线BF上取两点C,D,使CD=BC,
再作出BF的垂线DE,使A,C,E在一条直线上,
这时测得的DE的长就是AB的长.作出的图形如图所示:
∵AB⊥BF ED⊥BF
∴∠ABC=∠EDC=90°
又∵CD=BC
∠ACB=∠ECD
∴△ACB≌△ECD,
∴AB=DE.
点睛:本题主要考查了全等三角形的应用,关键是掌握判定两个三角形全等的判定方法:SSS,SAS,ASA,AAS.
16.a米.
【解析】试题分析:连结BM、MN,由SSS证明≌,可得∠CBM=∠NBM=45°,AB=AM=a.
试题解析:a米.连结BM、MN,
在△MCN中,∠MCN=180°-75°-45°=60°,CM=CN,
∴△MCN是等边三角形,
∴MC=MN,∠CBN=90°,∠BCN=45°,
∴BC=BN,在△MCB和△MNB中,
∴△MCB≌△MNB,
∴∠CBM=∠NBM=45°,
∴∠AMB=90°-45°,即∠ABM=∠AMB,
∴AB=AM=a,即房间的宽AB是a米.
17.见解析
【解析】分析:根据轮船在点A时两个灯塔与航线的夹角相等可得∠DAB=∠EAB,轮船到达点B时两个灯塔与航线的夹角仍然相等可得∠1=∠2,再根据等角的补角相等推出∠3=∠4,然后利用角边角定理证明△ABD与△ABE全等,然后根据全等三角形对应边相等即可证明.
本题解析:
到达点B时轮船与两个灯塔的距离相等。
理由如下:
根据题意得,∠DAB=∠EAB,∠1=∠2,
∵∠1+∠3=180°,∠2+∠4=180°,
∴∠3=∠4,
在△ABD与△ABE, ,
∴△ABD≌△ABE(ASA),
∴BD=BE.
即,到达点B时轮船与两个灯塔的距离相等.
18.(1)7米;(2)OM=15m;(3)玛丽在荡绳索过程中离地面的最低点的高度MN为2米.
【解析】试题分析:(1)作差.(2) 作AE⊥OM,BF⊥OM,证明在△AOE和△OBF相似,可以计算出OE+OF长度,最后算出OM长度.(3)利用勾股定理求出半径长度,作差求MN长度.
试题解析:
(1)10-3=7(米).
(2)作AE⊥OM于E,,BF⊥OM与F,
∵∠AOE+∠BOF=∠BOF+∠OBF=90°,
∴∠AOE=∠OBF,
在△AOE和△OBF中,
,
∴△AOE≌△OBF(AAS),
∴OE=BF,AE=OF,
即OE+OF=AE+BF=CD=17(m)
∵EF=EM﹣FM=AC﹣BD=10﹣3=7(m),
∴2EO+EF=17,
则2EO=10,
所以OE=5m,OF=12m,
所以OM=OF+FM=15m.
19.(1)图略 (2)AB=60m
【解析】分析:(1)认真读题,根据题意画出示意图;(2)结合题意分别求出AC、DC、DE的长,易得:AC=DC,∠BAC=∠EDC,∠DCE=∠ACB,根据全等三角形的判定定理可得△ABC≌△DEC,进而得到AB=DE,据此,可得出结果.
本题解析:(1)根据题意画出图形,如图所示.
(2)A、B两根电线杆之间的距离大约为36m.理由如下.
∵∠BAC=∠EDC=90°,60cm=0.6m,
∴AC=20×0.6=12m,
DC=20×0.6=12m,
DE=100×0.6=60m.
∵点E、C、B在一条直线上,
∴∠DCE=∠ACB.
∵∠BAC=∠EDC=90°,AC=DC,∠DCE=∠ACB,
∴△ABC≌△DEC.
∴AB=DE.
∵AB=DE,DE=60m,
∴AB=60m.
故A、B两根电线杆之间的距离大约为60m.
点睛:本题主要考查了全等三角形的应用,正确画出示意图,得到△ABC≌△DEC是解答此题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.5 利用三角形全等测距离同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.利用三角形全等测距离,实际是构建全等三角形,运用全等三角形的对应边相等,把较难测量和无法测量的距离转化成已知线段或较容易测量的线段的长度,从而得到被测距离.
2.数学方法:转化法,即把难以测量或无法测量的线段(或角)转化为易测量的线段(或角).
3. 步骤:①明确实际问题应该用哪些几何知识解决;②根据实际问题抽象出几何图形;③结合图形和题意分析已知条件;④找对解决问题的途径.
基础知识和能力拓展精练
一、选择题
1.利用三角形全等测量距离的原理是( )
A. 全等三角形对应角相等 B. 全等三角形对应边相等
C. 大小和形状相同的两个三角形全等 D. 三边对应相等的两个三角形全等
2.工人师傅常用角尺平分任意角,做法如下:如图,∠AOB是一个任意角,在OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点P的射线OP便是∠AOB的平分线,师傅这么做的依据是( )
A. SAS B. SSS C. 角平分线逆定理 D. AAS
3.如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,如图所示的这种方法,是利用了三角形全等中的( )
A. SSS B. ASA C. AAS D. SAS
4.某大学计划为新生配备如图①所示的折叠凳.图②是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30 cm,则由以上信息可推得CB的长度也为30 cm,依据是( )
A. SAS B. ASA C. SSS D. AAS
5.如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( )
A. SAS B. ASA C. AAS D. SSS
6.如图所示,已知BO=OC,AO=DO,CD=100m,则A,B两点间的距离( )
A. 大于100m B. 等于100m C. 小于100m D. 无法确定
7.如图,要测量河中礁石A离岸边B点的距离,采取的方法如下:顺着河岸的方向任作一条线段BC,作∠CBA'=∠CBA,∠BCA'=∠BCA.可得△A'BC≌△ABC,所以A'B=AB,所以测量A'B的长即可得AB的长.判定图中两个三角形全等的理由是( )
A. SAS B. ASA C. SSS D. AAS
8.如图,AA',BB'表示两根长度相同的木条,若O是AA',BB'的中点,经测量AB=9 cm,则容器的内径A'B'为( )
A. 8 cm B. 9 cm C. 10 cm D. 11 cm
二、填空题
9.如图,有一池塘,要测池塘两端A、B两点的距离,可先在平地上取一个可以直接到达A、B两点的C,连接AC并延长AC到点D,使CD=CA,连结BC并延长BC到点E,使CE=CB,连接DE,那么量出________的长就等于AB的长. 这是因为可根据________方法判定△ABC≌△DEC.
10.“三月三,放风筝”,如图是小明制作的风筝,他根据DE=DF,EH=FH,不用度量,就知道∠DEH=∠DFH,小明是通过全等三角形的识别得到的结论,请问小明用的识别方法是_____(用字母表示).
11.如图所示,要测量河宽AB的长,在AB的垂线BF上选取两点C,D,使CD=BC,再作DE⊥BF交BF于点D,且使A,C,E在同一条直线上,这时测得DE的长为30m,则河宽为______m.
12.如图所示,太阳光线AC与A′C′是平行的,AB表示一棵塔松,A′B′表示一棵小杨树,同一时刻两棵树的影长相等,已知塔松高6米,则小杨树高______.
13.如图,小明与小敏玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50cm,当小敏从水平位置CD下降40cm时,这时小明离地面的高度是___________。
三、解答题
14.在一次战役中,我军阵地与敌军碉堡隔河相望.为了炸掉这个碉堡,需要知道碉堡与我军阵地的距离.在不能过河测量又没有任何测量工具的情况下,如何测得距离?
一位战士的测量方法是:面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离。这是为什么呢?
15.如图所示,要测量河两岸相对的两点A、B的距离,因无法直接量出A、B两点的距离,请你设计一种方案,求出A、B的距离,并说明理由.
16.如图,房间内有一架梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为a米,此时梯子的倾斜角为75°,若梯子斜靠在另一面墙时,顶端距地面的垂直距离NB为b米,梯子的倾斜角为45°,则这个房间的宽AB是多少米?为什么?
17.如图,一艘轮船沿AC方向航行,轮船在点A时测得航线两侧的两个灯塔D、E与航线的夹角相等,当轮船到达点B时测得这两个灯塔与航线的夹角仍然相等,这时轮船与两个灯塔的距离是否相等?为什么?
18.在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,
(1)求高台A比矮台B高多少米?
(2)求旗杆的高度OM;
19.如图所示的A、B是两根呈南北方向排列的电线杆,A、B之间有一条小河,小刚想估测这两根电线杆之间的距离,于是小刚从A点开始向正西方向走了20步到达一棵大树C处,接着又向前走了20步到达D处,然后他左转90°直行,当他看到电线杆B、大树C和他自己现在所处的位置E恰在同一条直线上时,他从D位置走到E处恰好走了100步,利用上述数据,小刚测出了A、B两根电线杆之间的距离.
(1)请你根据上述的测量方法在原图上画出示意图;
(2)如果小刚一步大约60厘米,请你求A、B两根电线杆之间的距离并简述理由.
参考答案
1.B
【解析】利用三角形全等测量距离,是指无法直接测量时,我们通过构造全等的方法,然后借助全等三角形对应边相等,间接测量距离,故选B.
2.B
【解析】∵OM=ON,PM=PN,OP为公共边,
∴△MOP≌△NOP(SSS).
故选B.
3.D
【解析】由原题可得:
AC = DC
∠ACB=∠DCB
BC =BC
∴△ACB ≌△DCB(SAS)
∴AB = DB
故选D。
4.A
【解析】试题解析:∵O是AB、CD的中点,
∴OA=OB,OC=OD,
在△AOD和△BOC中,
,
∴△AOD≌△BOC(SAS),
∴CB=AD,
∵AD=30cm,
∴CB=30cm.
故选A.
5.A
【解析】在△COD和△AOB中, ,
∴△COD≌△AOB(SAS),
故选A.
6.B
【解析】∵AC=DB,AO=DO,
∴OB=OC,
又∠AOB=∠DOC,
∴△AOB≌△DOC,
∴AB=CD=100m.
故选B.
7.B
【解析】试题解析:在△△A'BC和△ABC中,
∵
∴△A'BC≌△ABC(ASA)
∴A'B=AB.
故选B.
8.B
【解析】解:由题意知:OA=OA′,∠AOB=∠A′OB′,OB=OB′,∴△AOB≌△A′OB′,∴A′B′=AB=9cm.故选B.
点睛:本题考查了全等三角形的判定及性质的应用;解答本题的关键是设计三角形全等,巧妙地借助两个三角形全等,寻找所求线段与已知线段之间的等量关系.
9. ED SAS
【解析】解:量出DE的长就等于AB的长.这是因为可根据SAS方法判定△ABC≌△DEC.故答案为:DE,SAS.
点睛:本题考查了全等三角形的应用,熟练掌握三角形全等的判定方法是解题的关键.
10.SSS
【解析】因为DE=DF,EH=FH,DH=DH,利用SSS可判定△DEH=△DFH,所以∠DEH=∠DFH,故答案为:SSS.
11.30
【解析】因为AB⊥BF,DE⊥BF,所以∠ABC=∠EDC=90°;
因为CD=BC,对顶角∠ACB=∠ECD,所以△ABC≌△EDC;
所以AB=DE=30,
故答案为:30.
点睛:本题考查全等三角形判定定理,有两角和其中一角的对边对应相等的两个三角形全等.注意隐含条件,对顶角相等.
12.6米
【解析】试题解析:∵ AC∥A′C′
∴∠ACB=∠A′C′B′(两直线平行,同位角相等)
∵ 树木是垂直地面生长的,
∴∠ABC=∠A′B′C′=90°,
∵∠ABC=∠A′B′C′,∠ACB=∠A′C′B′,AC∥A′C′,
∴△ABC≌△A′B′C′(两角及其夹边对应相等的两个三角形全等),
∴AB=A′B′=6米 (全等三角形的对应边相等),
所以小杨树的高为6米.
故答案为:6米.
13.90cm
【解析】试题解析:∵O是CD和FG的中点,
∴FO=OG,CO=DO,
又∠FOC=∠GOD,
∴ΔFOC≌ΔGOD,
∴FC=GD=40cm,
∴小明离地面的高度是:50+40=90cm.
14.见解析
【解析】分析:根据三角形全等的判定方法,得到一些相应线段或角相等,在现实生活中有许多应用的实例.
本题解析:
在本题中,根据题意可以知道,满足了三个条件:
(1)身体高度一定,(2)帽檐处的角度一定,(3)脚下的直角一定,
故根据ASA判定方法,可以得到两个三角形全全等,
∴距离相等。
理由是:在△AHB与中,
∴
点睛:本题主要考查作图—应用与设计作图,根据题意画出示意图,并熟练掌握全等三角形的判定与性质是解题的关键.
15.见解析
【解析】分析:根据题中垂直可得到一组角相等,再根据对顶角相等,已知一组边相等,得到三角形全等的三个条件,于是根据ASA可得到三角形全等,全等三角形的对应边相等,得结论.
本题解析:
在AB的垂线BF上取两点C,D,使CD=BC,
再作出BF的垂线DE,使A,C,E在一条直线上,
这时测得的DE的长就是AB的长.作出的图形如图所示:
∵AB⊥BF ED⊥BF
∴∠ABC=∠EDC=90°
又∵CD=BC
∠ACB=∠ECD
∴△ACB≌△ECD,
∴AB=DE.
点睛:本题主要考查了全等三角形的应用,关键是掌握判定两个三角形全等的判定方法:SSS,SAS,ASA,AAS.
16.a米.
【解析】试题分析:连结BM、MN,由SSS证明≌,可得∠CBM=∠NBM=45°,AB=AM=a.
试题解析:a米.连结BM、MN,
在△MCN中,∠MCN=180°-75°-45°=60°,CM=CN,
∴△MCN是等边三角形,
∴MC=MN,∠CBN=90°,∠BCN=45°,
∴BC=BN,在△MCB和△MNB中,
∴△MCB≌△MNB,
∴∠CBM=∠NBM=45°,
∴∠AMB=90°-45°,即∠ABM=∠AMB,
∴AB=AM=a,即房间的宽AB是a米.
17.见解析
【解析】分析:根据轮船在点A时两个灯塔与航线的夹角相等可得∠DAB=∠EAB,轮船到达点B时两个灯塔与航线的夹角仍然相等可得∠1=∠2,再根据等角的补角相等推出∠3=∠4,然后利用角边角定理证明△ABD与△ABE全等,然后根据全等三角形对应边相等即可证明.
本题解析:
到达点B时轮船与两个灯塔的距离相等。
理由如下:
根据题意得,∠DAB=∠EAB,∠1=∠2,
∵∠1+∠3=180°,∠2+∠4=180°,
∴∠3=∠4,
在△ABD与△ABE, ,
∴△ABD≌△ABE(ASA),
∴BD=BE.
即,到达点B时轮船与两个灯塔的距离相等.
18.(1)7米;(2)OM=15m;(3)玛丽在荡绳索过程中离地面的最低点的高度MN为2米.
【解析】试题分析:(1)作差.(2) 作AE⊥OM,BF⊥OM,证明在△AOE和△OBF相似,可以计算出OE+OF长度,最后算出OM长度.(3)利用勾股定理求出半径长度,作差求MN长度.
试题解析:
(1)10-3=7(米).
(2)作AE⊥OM于E,,BF⊥OM与F,
∵∠AOE+∠BOF=∠BOF+∠OBF=90°,
∴∠AOE=∠OBF,
在△AOE和△OBF中,
,
∴△AOE≌△OBF(AAS),
∴OE=BF,AE=OF,
即OE+OF=AE+BF=CD=17(m)
∵EF=EM﹣FM=AC﹣BD=10﹣3=7(m),
∴2EO+EF=17,
则2EO=10,
所以OE=5m,OF=12m,
所以OM=OF+FM=15m.
19.(1)图略 (2)AB=60m
【解析】分析:(1)认真读题,根据题意画出示意图;(2)结合题意分别求出AC、DC、DE的长,易得:AC=DC,∠BAC=∠EDC,∠DCE=∠ACB,根据全等三角形的判定定理可得△ABC≌△DEC,进而得到AB=DE,据此,可得出结果.
本题解析:(1)根据题意画出图形,如图所示.
(2)A、B两根电线杆之间的距离大约为36m.理由如下.
∵∠BAC=∠EDC=90°,60cm=0.6m,
∴AC=20×0.6=12m,
DC=20×0.6=12m,
DE=100×0.6=60m.
∵点E、C、B在一条直线上,
∴∠DCE=∠ACB.
∵∠BAC=∠EDC=90°,AC=DC,∠DCE=∠ACB,
∴△ABC≌△DEC.
∴AB=DE.
∵AB=DE,DE=60m,
∴AB=60m.
故A、B两根电线杆之间的距离大约为60m.
点睛:本题主要考查了全等三角形的应用,正确画出示意图,得到△ABC≌△DEC是解答此题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
