5.2.1平行线 课件
图片预览







文档简介
课件27张PPT。5.2.1平行线想一想: 说一说:下面图片中哪些地方给我们平行的形象?数学来源于生活短池游泳双杠
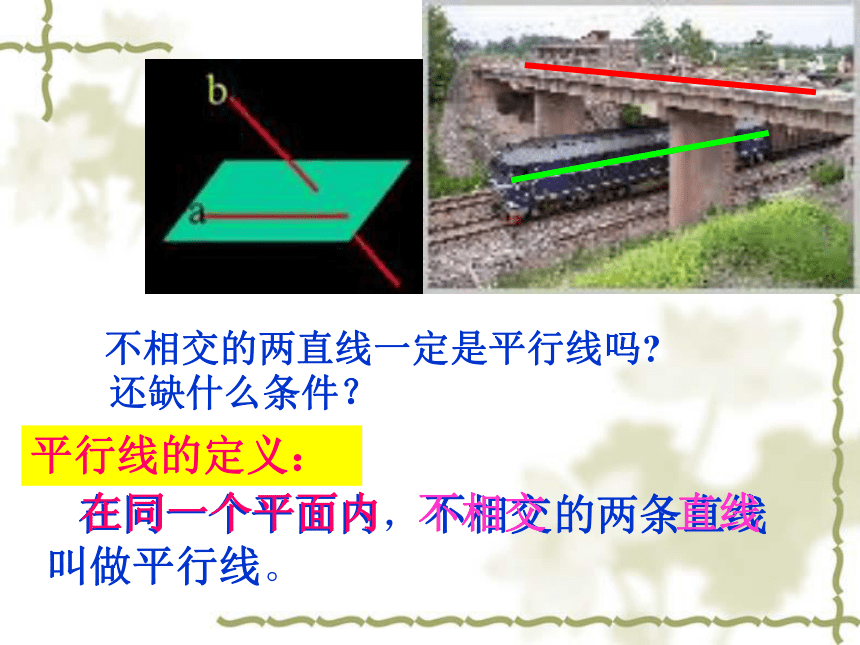
不相交的两直线一定是平行线吗? 平行线的定义: 在同一个平面内,不相交的两条直线叫做平行线。
直线不相交在同一个平面内还缺什么条件?
1、在同 一平面内平行线有什么特征?2、不相交2、既然生活中有这么多的平行线的形象,那么
平行线能给我们什么感受呢?3、如果铁轨、扶梯、做操队伍不平行会怎么样?有感而发:1、在生活中,你还能举出一些平行线的例子吗?生活中的平行线的形象给我们整齐、美观、协调的感觉,因此平时老师总是要求我们桌椅摆放、做操队伍排列都要前后左右对齐。
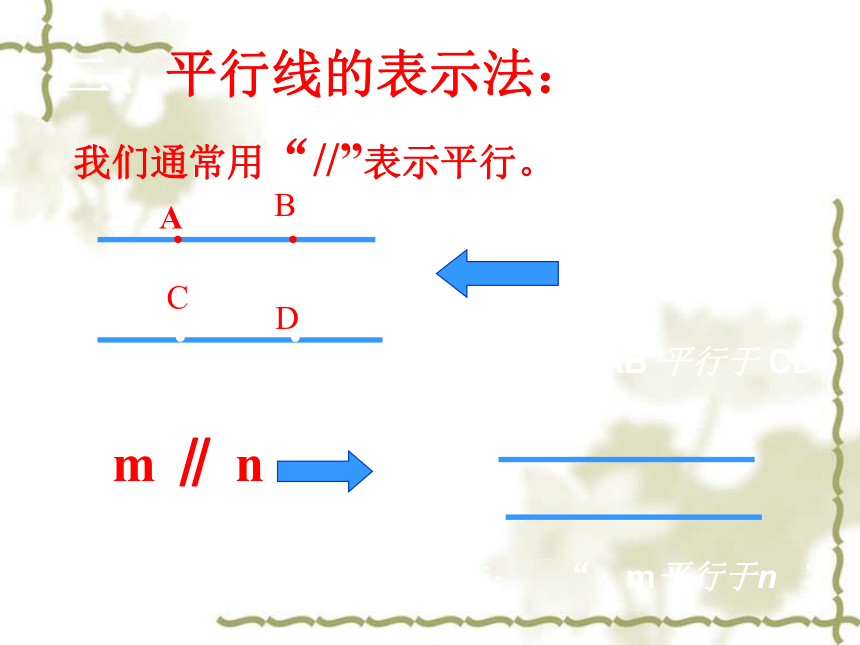
我们通常用“//”表示平行。二、平行线的表示法:读作: “AB 平行于 CD” 读作: “ m平行于n ” 练一练:
用符号“∥”表示图中平行四边形的两组对边分别平行。C D
A B
一个长方体如图,和AA'平行的棱有多少条?和AB平行的棱有多少条?请用符号把它们表示出来。和AA'平行的棱有3条:BB'∥AA', CC'∥AA',
DD'∥AA'.和AB平行的棱有3条:A'B'∥AB, C'D'∥AB,
CD∥AB.讨论与探究1.平行线要求在同一平面内,那么在同一平面内两直线的位置关系一共有几种呢?(小组先讨论再实践)结论:在同一平面内,两直线的位置
关系有平行与相交两种。2、平行线的画法:(1)放(2)靠(3)移(4)画·AAABPCD 如图,在△ABC中,P是边AC上一点.过点P分别画AB、BC的平行线ABC.P现学现卖给你一条直线AB,如何画出它的平行线呢?可以画多少条平行线呢?动手实践:过直线AB外一点P作直线AB的平行线,看看你能作出吗?能作出几条?· A B P动手实践:结 论:经过直线外一点,有且只有一条直线与这条直线平行.(平行公理)说明:人们在长期实践中总结出来的结论叫基本
事实,也称为公理,它可以作为以后推理的依据.如图:三条直线AB、CD、EF。如果AB//EF ,CD//EF,
那么直线AB与CD可能相交吗?FEDCBA假设AB与CD相交,
设AB与CD相交于P因为AB//EF,CD//EF
于是过点P就有两条直线AB
CD都与EF平行。
根据平行公理,这是不可能的
也就是说,AB与CD不能相交,
只能平行。平行公理的推论:如果两条直线都和第三条直线平行,
那么这两条直线也互相平行几何语言表达:
a//c , c//b(已知)
? a//b(如果两条直线都和第三条直线平行,
那么这两条直线也互相平行)?由此可见:平行具有传递性填空
1.在同一平面内,两条直线的位置关系有_____种.两条直线相交,交点的个数是_____个,两条直线平行,交点的个数是_____个.
2.在同一平面内,一条直线和两条平行线中的一条直线相交,那么这条直线与平行线中的另一条必__________.
3、在同一平面内,与已知直线L平行的直线有______条,而经过L外一点,与已知直线L平行的直线有且只有 条。210相交无数一温故而知新:
.4.在同一平面内,三条直线的交点个数可能是 .变式:下列说法正确的个数是( )(1)两条直线不相交就平行。
(2)在同一平面内,两条平行的直线有且只有一个交点
(3)过一点有且只有一条直线与已知直线平行
(4)平行于同一直线的两条直线互相平行
(5)两直线的位置关系只有相交与平行A、0 B、1 C、2 D、4 B温故而知新:
.5、下列推理正确的是( )A、因为a // d,b // c,所以c // d;
B、因为a // c,b // d,所以c // d;
C、因为a // b,a // c,所以b // c;
D、因为a // b,c // d,所以a // c。温故而知新:
.C6.下列说法正确的是( ) A.经过一点有且只有一条直线与已知直线平行 B.经过一点有无数条直线与已知直线平行 C.经过一点有一条直线与已知直线平行 D.经过直线外一点有且只有一条直线与已知直线平行温故而知新:
.D7.温故而知新:
.B9、完成下列推理,并在括号内注明理由。
(1)如图1所示,因为AB // DE,BC // DE(已知)。所以
A,B,C三点___________( )
(2)如图2所示,因为AB // CD,CD // EF(已知),所以
________ // _________( )
在同一直线上经过直线外一点,有且只有一条直线与这条直线平行ABEF如果两条直线都和第三条直线平行,
那么这两条直线也互相平行温故而知新:
.10.若∠ 与∠ 是同旁内角,且 ∠ =50°,则∠ 的度数是( ) A.50° B.130° C.50°或130° D.不能确定 11、在同一平面内,直线a与b满足下列条件,写出其对应的位置关系
(1)a与b没有公共点,则 a与b ;
(2)a与b有且只有一个公共点,则a与b ;温故而知新:
. 本节课你的收获是什么?小结(1) 平行线的定义; (2)平行线的表示方法;(3)两条直线在同一平面内的位置关系。(4)平行线的画法。(5)平行线公理(6)平行线公理的推论。
不相交的两直线一定是平行线吗? 平行线的定义: 在同一个平面内,不相交的两条直线叫做平行线。
直线不相交在同一个平面内还缺什么条件?
1、在同 一平面内平行线有什么特征?2、不相交2、既然生活中有这么多的平行线的形象,那么
平行线能给我们什么感受呢?3、如果铁轨、扶梯、做操队伍不平行会怎么样?有感而发:1、在生活中,你还能举出一些平行线的例子吗?生活中的平行线的形象给我们整齐、美观、协调的感觉,因此平时老师总是要求我们桌椅摆放、做操队伍排列都要前后左右对齐。
我们通常用“//”表示平行。二、平行线的表示法:读作: “AB 平行于 CD” 读作: “ m平行于n ” 练一练:
用符号“∥”表示图中平行四边形的两组对边分别平行。C D
A B
一个长方体如图,和AA'平行的棱有多少条?和AB平行的棱有多少条?请用符号把它们表示出来。和AA'平行的棱有3条:BB'∥AA', CC'∥AA',
DD'∥AA'.和AB平行的棱有3条:A'B'∥AB, C'D'∥AB,
CD∥AB.讨论与探究1.平行线要求在同一平面内,那么在同一平面内两直线的位置关系一共有几种呢?(小组先讨论再实践)结论:在同一平面内,两直线的位置
关系有平行与相交两种。2、平行线的画法:(1)放(2)靠(3)移(4)画·AAABPCD 如图,在△ABC中,P是边AC上一点.过点P分别画AB、BC的平行线ABC.P现学现卖给你一条直线AB,如何画出它的平行线呢?可以画多少条平行线呢?动手实践:过直线AB外一点P作直线AB的平行线,看看你能作出吗?能作出几条?· A B P动手实践:结 论:经过直线外一点,有且只有一条直线与这条直线平行.(平行公理)说明:人们在长期实践中总结出来的结论叫基本
事实,也称为公理,它可以作为以后推理的依据.如图:三条直线AB、CD、EF。如果AB//EF ,CD//EF,
那么直线AB与CD可能相交吗?FEDCBA假设AB与CD相交,
设AB与CD相交于P因为AB//EF,CD//EF
于是过点P就有两条直线AB
CD都与EF平行。
根据平行公理,这是不可能的
也就是说,AB与CD不能相交,
只能平行。平行公理的推论:如果两条直线都和第三条直线平行,
那么这两条直线也互相平行几何语言表达:
a//c , c//b(已知)
? a//b(如果两条直线都和第三条直线平行,
那么这两条直线也互相平行)?由此可见:平行具有传递性填空
1.在同一平面内,两条直线的位置关系有_____种.两条直线相交,交点的个数是_____个,两条直线平行,交点的个数是_____个.
2.在同一平面内,一条直线和两条平行线中的一条直线相交,那么这条直线与平行线中的另一条必__________.
3、在同一平面内,与已知直线L平行的直线有______条,而经过L外一点,与已知直线L平行的直线有且只有 条。210相交无数一温故而知新:
.4.在同一平面内,三条直线的交点个数可能是 .变式:下列说法正确的个数是( )(1)两条直线不相交就平行。
(2)在同一平面内,两条平行的直线有且只有一个交点
(3)过一点有且只有一条直线与已知直线平行
(4)平行于同一直线的两条直线互相平行
(5)两直线的位置关系只有相交与平行A、0 B、1 C、2 D、4 B温故而知新:
.5、下列推理正确的是( )A、因为a // d,b // c,所以c // d;
B、因为a // c,b // d,所以c // d;
C、因为a // b,a // c,所以b // c;
D、因为a // b,c // d,所以a // c。温故而知新:
.C6.下列说法正确的是( ) A.经过一点有且只有一条直线与已知直线平行 B.经过一点有无数条直线与已知直线平行 C.经过一点有一条直线与已知直线平行 D.经过直线外一点有且只有一条直线与已知直线平行温故而知新:
.D7.温故而知新:
.B9、完成下列推理,并在括号内注明理由。
(1)如图1所示,因为AB // DE,BC // DE(已知)。所以
A,B,C三点___________( )
(2)如图2所示,因为AB // CD,CD // EF(已知),所以
________ // _________( )
在同一直线上经过直线外一点,有且只有一条直线与这条直线平行ABEF如果两条直线都和第三条直线平行,
那么这两条直线也互相平行温故而知新:
.10.若∠ 与∠ 是同旁内角,且 ∠ =50°,则∠ 的度数是( ) A.50° B.130° C.50°或130° D.不能确定 11、在同一平面内,直线a与b满足下列条件,写出其对应的位置关系
(1)a与b没有公共点,则 a与b ;
(2)a与b有且只有一个公共点,则a与b ;温故而知新:
. 本节课你的收获是什么?小结(1) 平行线的定义; (2)平行线的表示方法;(3)两条直线在同一平面内的位置关系。(4)平行线的画法。(5)平行线公理(6)平行线公理的推论。
