28.2解直角三角形的应用(方位角) 课件
文档属性
| 名称 | 28.2解直角三角形的应用(方位角) 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-01 20:07:37 | ||
图片预览



文档简介
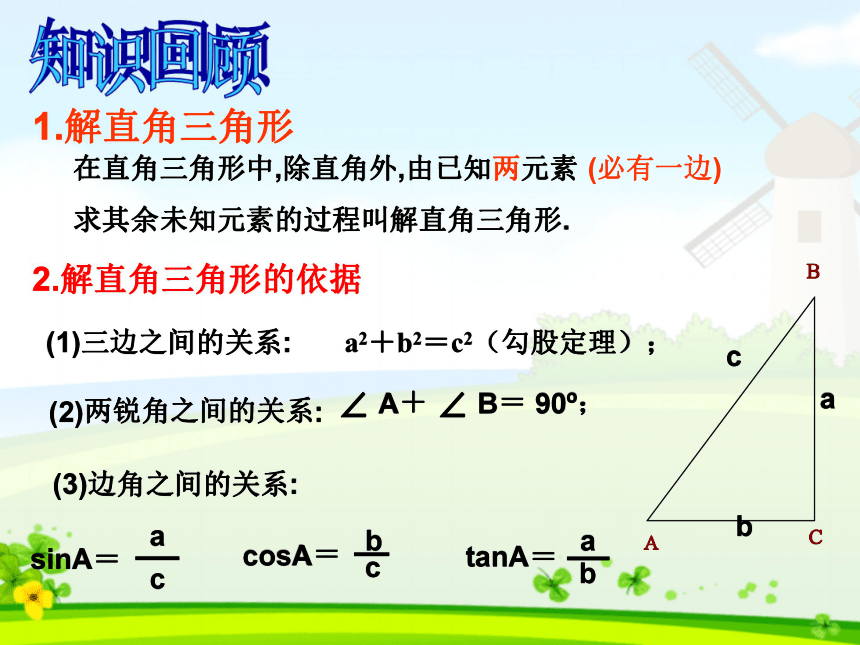
课件19张PPT。28.2解直角三角形的应用(方位角)在直角三角形中,除直角外,由已知两元素
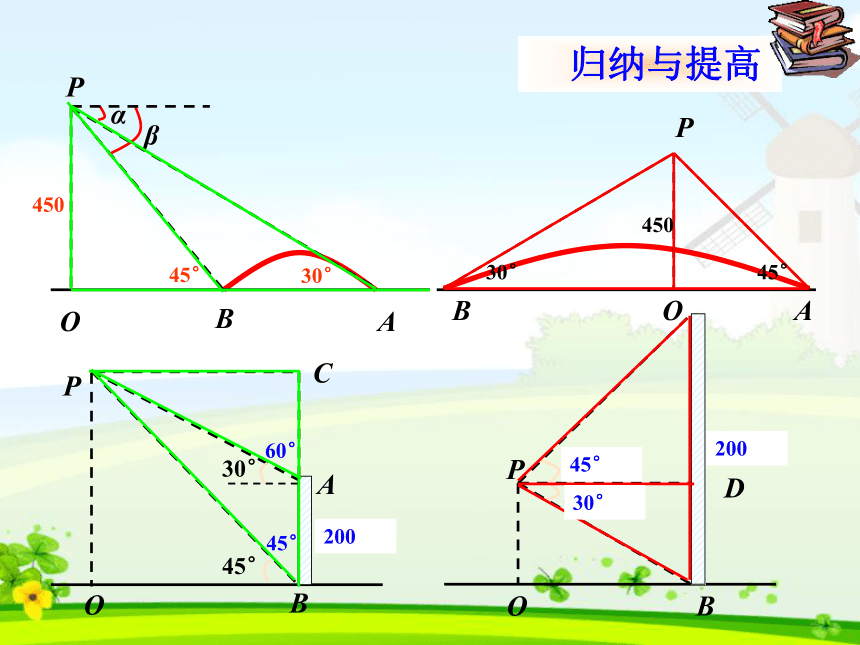
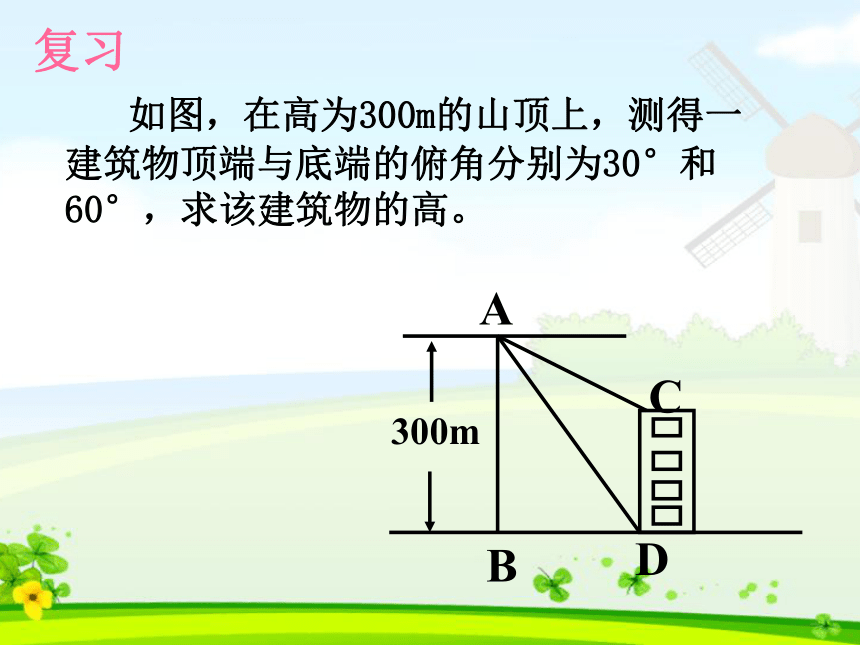
求其余未知元素的过程叫解直角三角形.1.解直角三角形(1)三边之间的关系:a2+b2=c2(勾股定理);2.解直角三角形的依据(2)两锐角之间的关系:∠ A+ ∠ B= 90o;(3)边角之间的关系:sinA=知识回顾(必有一边)45°30°45060°45°20020045°30°30°45°4501.数形结合思想.方法:把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,构造出直角三角形.解题思想与方法小结:2.方程思想.3.转化(化归)思想. 如图,在高为300m的山顶上,测得一建筑物顶端与底端的俯角分别为30°和60°,求该建筑物的高。复习ABCD方位角的定义: 指北或指南方向线与目标方向线所
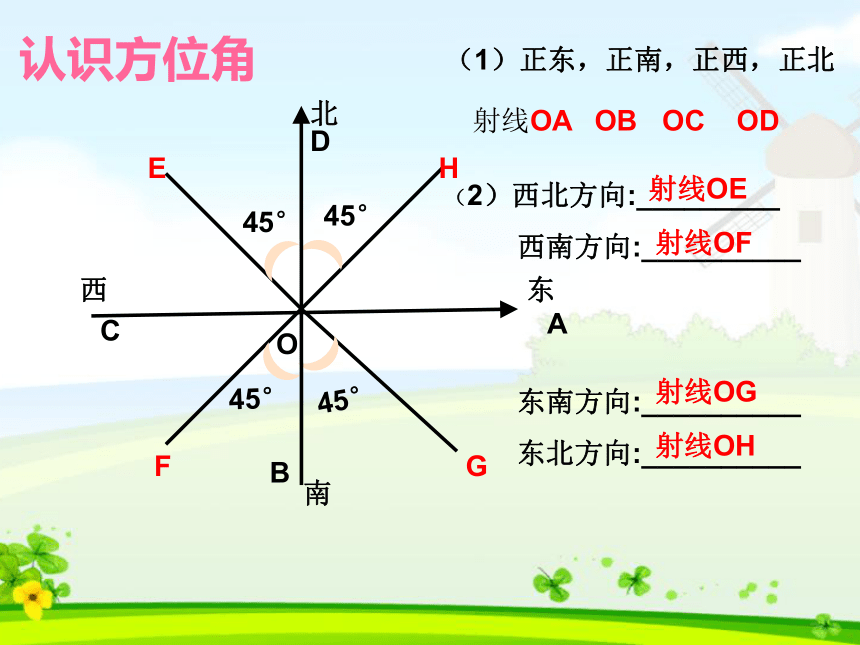
成的小于90°的角叫做方位角。东西北南O(1)正东,正南,正西,正北(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OAABCDOBOCOD45°射线OE射线OF射线OG射线OH45°45°45°认识方位角O北南西东 (3)南偏西25°25° 北偏西70° 南偏东60°射线OA射线OB射线OC70°60°认识方位角归纳方位角问题的实际应用题解法: 直接或间接把问题放在直角三角形中,解题时应善于发现直角三角形,用三角函数等知识解决问题。探究例题:如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它正沿着正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?小结解直角三角形的应用:(1)将实际问题抽象为数学问题(画出平面
图形,转化为解直角三角形的问题);(2)根据条件的特点,适当选用锐角三角
函数等知识去解直角三角形;(3)得到数学问题答案;(4)得到实际问题答案;1、海中有一个小岛A,它的周围8海里内有暗礁,鱼船跟踪鱼群由西向东航行。在B点测得小岛A在北偏东60°方向上,航行12海里到达点D,这时测得小岛A在北偏东30°方向上,如果鱼船不改变航线继续向东航行,有没有触礁的危险?当堂练习答:货轮无触礁危险。在Rt△ADC中,
∵ tan∠DCA=------
∴AD= tan600x= x在Rt△ADB中,
∵ tan30?= ---- = --------AD≈12×1.732 =20.784 > 20 解:过点A作AD⊥BC于D,ABDCNN1二、探究24海里XADDCADBD 3 xX=12X+24设CD=x,则BD=X+24
例、如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,,航行24海里到C,在B处见岛A在北偏西60?.在c见岛A在北偏西30?,货轮继续向西航行,有无触礁的危险?当堂练习2、如图,某船以29.8海里/时的速度向正北方向航行,在A处测得灯塔C在该船的北偏东32°方向上,半小时后该船航行到点B处,发现此时灯塔C与船的距离最短。
(1)在图上标出点B的位置;
(2)求灯塔C到B处的距离(精确到0.1海里)。
3、如图,小岛A在港口P的南偏西45°方向,距离港口81海里处,甲船从小岛A出发,沿AP方向以9海里/时的速度驶向港口;乙船从港口P出发,沿南偏东60°方向,以18海里/时的速度驶离港口。已知两船同时出发。
(1)出发后几小时两船与港口P的距离相等?
(2)出发后几小时乙船在甲船的正东方向?
当堂练习4、如图,海关缉私艇在A处接到情报,在A的北偏西60°方向的B处发现一可疑船只正以24海里/时的速度向正东方向航行,于是该艇立即沿北偏西45°方向前进,经过1小时航行,恰好在C处截住可疑船只,求缉私艇的速度。当堂练习
5.国外船只,除特许外,不得进入我国海洋100海里以内的区域,如图,设A、B是我们的观察站,A和B 之间的距离为157.73海里,海岸线是过A、B的一条直线,一外国船只在P点,在A点测得∠BAP=450,同时在B点测得∠ABP=600,问此时是否要向外国船只发出警告,令其退出我国海域.挑战自我谈谈本节课你的收获作业:书93页9.10(认真画图,其实很简单哟)练习:专题训练测试题请认真独立完成!相信你是最棒的!!加油
求其余未知元素的过程叫解直角三角形.1.解直角三角形(1)三边之间的关系:a2+b2=c2(勾股定理);2.解直角三角形的依据(2)两锐角之间的关系:∠ A+ ∠ B= 90o;(3)边角之间的关系:sinA=知识回顾(必有一边)45°30°45060°45°20020045°30°30°45°4501.数形结合思想.方法:把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,构造出直角三角形.解题思想与方法小结:2.方程思想.3.转化(化归)思想. 如图,在高为300m的山顶上,测得一建筑物顶端与底端的俯角分别为30°和60°,求该建筑物的高。复习ABCD方位角的定义: 指北或指南方向线与目标方向线所
成的小于90°的角叫做方位角。东西北南O(1)正东,正南,正西,正北(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OAABCDOBOCOD45°射线OE射线OF射线OG射线OH45°45°45°认识方位角O北南西东 (3)南偏西25°25° 北偏西70° 南偏东60°射线OA射线OB射线OC70°60°认识方位角归纳方位角问题的实际应用题解法: 直接或间接把问题放在直角三角形中,解题时应善于发现直角三角形,用三角函数等知识解决问题。探究例题:如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它正沿着正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?小结解直角三角形的应用:(1)将实际问题抽象为数学问题(画出平面
图形,转化为解直角三角形的问题);(2)根据条件的特点,适当选用锐角三角
函数等知识去解直角三角形;(3)得到数学问题答案;(4)得到实际问题答案;1、海中有一个小岛A,它的周围8海里内有暗礁,鱼船跟踪鱼群由西向东航行。在B点测得小岛A在北偏东60°方向上,航行12海里到达点D,这时测得小岛A在北偏东30°方向上,如果鱼船不改变航线继续向东航行,有没有触礁的危险?当堂练习答:货轮无触礁危险。在Rt△ADC中,
∵ tan∠DCA=------
∴AD= tan600x= x在Rt△ADB中,
∵ tan30?= ---- = --------AD≈12×1.732 =20.784 > 20 解:过点A作AD⊥BC于D,ABDCNN1二、探究24海里XADDCADBD 3 xX=12X+24设CD=x,则BD=X+24
例、如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,,航行24海里到C,在B处见岛A在北偏西60?.在c见岛A在北偏西30?,货轮继续向西航行,有无触礁的危险?当堂练习2、如图,某船以29.8海里/时的速度向正北方向航行,在A处测得灯塔C在该船的北偏东32°方向上,半小时后该船航行到点B处,发现此时灯塔C与船的距离最短。
(1)在图上标出点B的位置;
(2)求灯塔C到B处的距离(精确到0.1海里)。
3、如图,小岛A在港口P的南偏西45°方向,距离港口81海里处,甲船从小岛A出发,沿AP方向以9海里/时的速度驶向港口;乙船从港口P出发,沿南偏东60°方向,以18海里/时的速度驶离港口。已知两船同时出发。
(1)出发后几小时两船与港口P的距离相等?
(2)出发后几小时乙船在甲船的正东方向?
当堂练习4、如图,海关缉私艇在A处接到情报,在A的北偏西60°方向的B处发现一可疑船只正以24海里/时的速度向正东方向航行,于是该艇立即沿北偏西45°方向前进,经过1小时航行,恰好在C处截住可疑船只,求缉私艇的速度。当堂练习
5.国外船只,除特许外,不得进入我国海洋100海里以内的区域,如图,设A、B是我们的观察站,A和B 之间的距离为157.73海里,海岸线是过A、B的一条直线,一外国船只在P点,在A点测得∠BAP=450,同时在B点测得∠ABP=600,问此时是否要向外国船只发出警告,令其退出我国海域.挑战自我谈谈本节课你的收获作业:书93页9.10(认真画图,其实很简单哟)练习:专题训练测试题请认真独立完成!相信你是最棒的!!加油
