1.4 二次函数与一元二次方程的联系课件 (共49张PPT)
文档属性
| 名称 | 1.4 二次函数与一元二次方程的联系课件 (共49张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 801.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-01 00:00:00 | ||
图片预览







文档简介
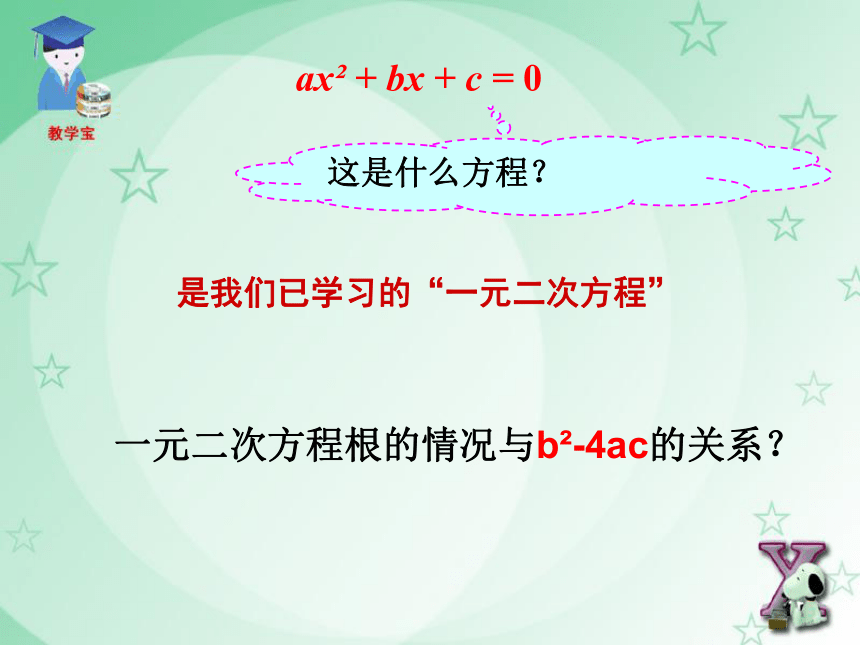
课件49张PPT。二次函数与一元二次方程二次函数的一般式:(a≠0)______是自变量,____是____的函数。xyx 当 y = 0 时,ax2 + bx + c = 0ax2 + bx + c = 0这是什么方程? 是我们已学习的“一元二次方程”一元二次方程根的情况与b2-4ac的关系?我们知道:代数式b2-4ac对于方程的根起着关键的作用.一元二次方程根的情况与b2-4ac的关系探究一:二次函数y=ax2+bx+c与一元二次方程ax2+bx+c=0有什么关系?1、一次函数y=kx+b与一元一次方程kx+b=0有什么关系?
2、你能否用类比的方法猜想二次函数y=ax2+bx+c与
一元二次方程ax2+bx+c=0的关系?
以 40 m /s的速度将小球沿与地面成 30°角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气阻力,球的飞行高度 h (单位:m)与飞行时间 t (单位:s)之间具有关系:h= 20 t – 5 t 2
考虑下列问题:
(1)球的飞行高度能否达到 15 m? 若能,需要多少时间?
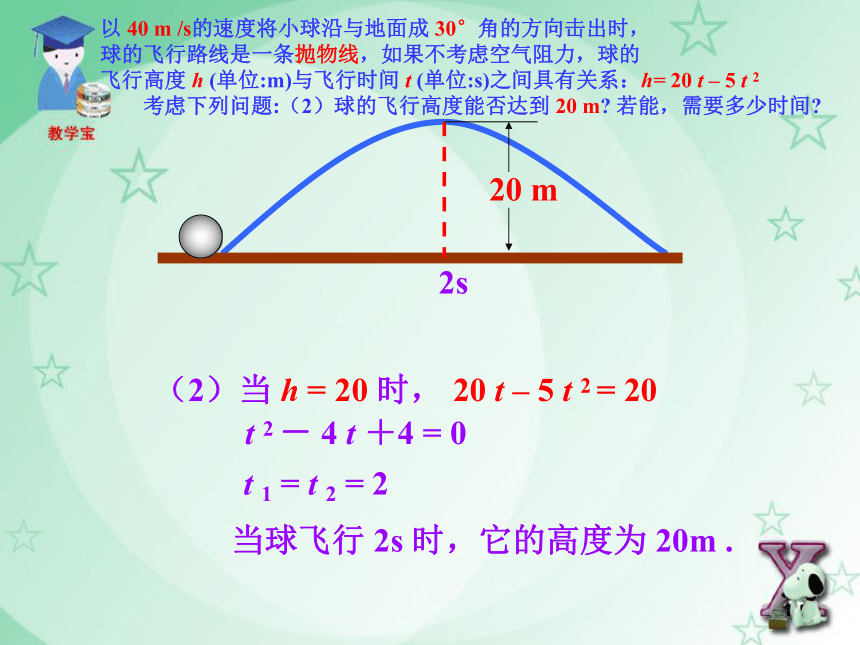
(2)球的飞行高度能否达到 20 m? 若能,需要多少时间?
(3)球的飞行高度能否达到 20.5 m?为什么?
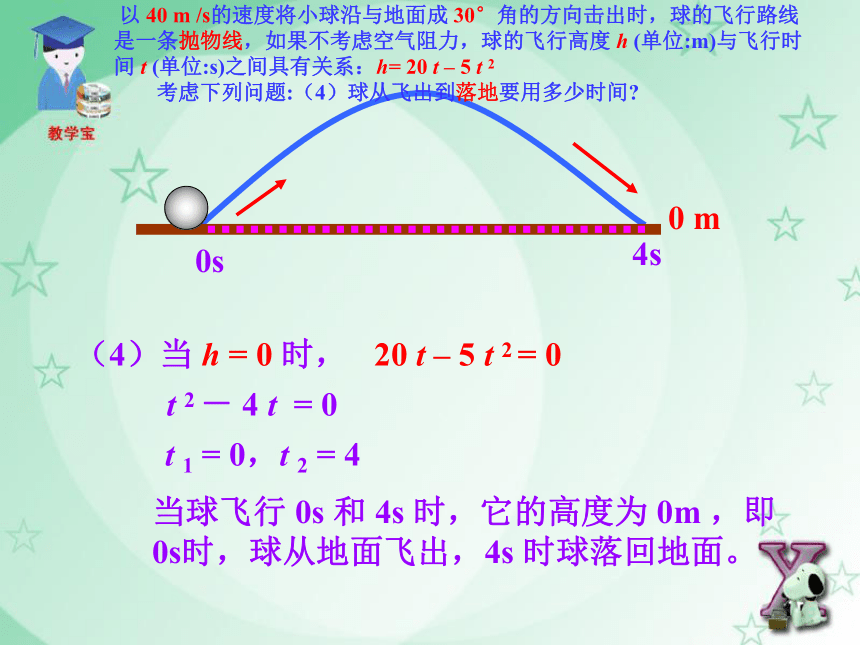
(4)球从飞出到落地要用多少时间?解:(1)当 h = 15 时,20 t – 5 t 2 = 15t 2 - 4 t +3 = 0t 1 = 1,t 2 = 3当球飞行 1s 和 3s 时,它的高度为 15m .1s3s15 m 以 40 m /s的速度将小球沿与地面成 30°角的方向击出时,
球的飞行路线是一条抛物线,如果不考虑空气阻力,球
的飞行高度 h (单位:m)与飞行时间 t (单位:s)之间具有关系:h= 20 t – 5 t 2
考虑下列问题:
(1)球的飞行高度能否达到 15 m? 若能,需要多少时间?
(2)当 h = 20 时,20 t – 5 t 2 = 20t 2 - 4 t +4 = 0t 1 = t 2 = 2当球飞行 2s 时,它的高度为 20m .2s20 m以 40 m /s的速度将小球沿与地面成 30°角的方向击出时,
球的飞行路线是一条抛物线,如果不考虑空气阻力,球的
飞行高度 h (单位:m)与飞行时间 t (单位:s)之间具有关系:h= 20 t – 5 t 2
考虑下列问题:(2)球的飞行高度能否达到 20 m? 若能,需要多少时间?
(3)当 h = 20.5 时,20 t – 5 t 2 = 20.5t 2 - 4 t +4.1 = 0因为(-4)2-4×4.1 < 0 ,所以方程无实根。
球的飞行高度达不到 20.5 m.20.5 m以 40 m /s的速度将小球沿与地面成 30°角的方向击出时,球的飞行路线
是一条抛物线,如果不考虑空气阻力,球的飞行高度 h (单位:m)与飞行
时间 t (单位:s)之间具有关系:h= 20 t – 5 t 2
考虑下列问题:(3)球的飞行高度能否达到 20.5 m?为什么?
(4)当 h = 0 时,20 t – 5 t 2 = 0t 2 - 4 t = 0t 1 = 0,t 2 = 4当球飞行 0s 和 4s 时,它的高度为 0m ,即 0s时,球从地面飞出,4s 时球落回地面。0s4s0 m 以 40 m /s的速度将小球沿与地面成 30°角的方向击出时,球的飞行路线
是一条抛物线,如果不考虑空气阻力,球的飞行高度 h (单位:m)与飞行时
间 t (单位:s)之间具有关系:h= 20 t – 5 t 2
考虑下列问题:(4)球从飞出到落地要用多少时间?
从上面发现,二次函数y=ax2+bx+c何时为一元二次方程?一般地,当y取定值时,二次函数为一元二次方程。如:y=5时,则5=ax2+bx+c就是一个一元二次方程。
自由讨论例如,已知二次函数y=-X2+4x的值为3,求自变量x的值.就是求方程3=-X2+4x的解,例如,解方程X2-4x+3=0就是已知二次函数y=X2-4x+3的值为0,求自变量x的值.已知二次函数,求自变量的值解一元二次方程的根二次函数与一元二次方程的关系(1)1、二次函数y = x2+x-2 , y = x2 - 6x +9 , y = x2 – x+ 1的图象如图所示。(1).每个图象与x轴有几个交点?
(2).一元二次方程? x2+x-2=0 , x2 - 6x +9=0有几个根?
验证一下一元二次方程x2 – x+ 1 =0有根吗?
(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与
一元二次方程ax2+bx+c=0的根有什么关系?答:2个,1个,0个边观察边思考(3),二次函数y=ax2+bx+c的图象和x轴交点的坐标与 一元二次方程ax2+bx+c=0的根有什么关系?(-2,0),(1,0)x1=-2,x2=1(3,0)x1=x2=3无交点无实根 抛物线y=ax2+bx+c与x轴交点的横坐标是方程ax2+bx+c =0的根。归纳一元二次方程ax2+bx+c=0的两个根为x1,x2 ,则抛物线 y=ax2+bx+c与x轴的交点坐标是(x1,0),(x2,0)
下列二次函数的图象与 x 轴有交点吗? 若有,求出交点坐标.
(1) y = 2x2+x-3
(2) y = 4x2 -4x +1
(3) y = x2 – x+ 1令 y= 0,解一元二次方程的根(1) y = 2x2+x-3解:当 y = 0 时,2x2+x-3 = 0(2x+3)(x-1) = 0x 1 = ,x 2 = 1 所以与 x 轴有交点,有两个交点。y =a(x-x1)(x- x 2)二次函数的交点式 (2) y = 4x2 -4x +1解:当 y = 0 时,4x2 -4x +1 = 0(2x-1)2 = 0x 1 = x 2 = 所以与 x 轴有一个交点。(3) y = x2 – x+ 1解:当 y = 0 时,x2 – x+ 1 = 0 所以与 x 轴没有交点。因为(-1)2-4×1×1 = -3 < 0确定二次函数图象与 x 轴的位置关系解一元二次方程的根二次函数与一元二次方程的关系(2)有两个根
有一个根(两个相同的根)
没有根有两个交点
有一个交点
没有交点b2 – 4ac > 0b2 – 4ac = 0b2 – 4ac < 0二次函数 y=ax2+bx+c 的图象和x轴交点的三种情况与一元二次方程根的关系ax2+bx+c = 0 的根 y=ax2+bx+c 的图象与x轴 若抛物线 y=ax2+bx+c 与 x 轴有交点,则________________ 。b2 – 4ac ≥ 0△>0△=0△<0oxy△ = b2 – 4ac△>0△=0△<0oxy△ = b2 – 4ac 二次函数 y=ax2+bx+c 的图象和x轴交点的三种情况与一元二次方程根的关系:有两个交点有两个不相等的实数根只有一个交点有两个相等的实数根没有交点没有实数根b2 – 4ac > 0b2 – 4ac = 0b2 – 4ac < 0与x轴有两个不
同的交点
(x1,0)
(x2,0)有两个不同的解x=x1,x=x2b2-4ac>0与x轴有唯一个
交点有两个相等的解
x1=x2=b2-4ac=0与x轴没有
交点没有实数根b2-4ac<02.抛物线y=2x2-3x-5 与x轴有无交点?若无说出理由,若有求出交点坐标?1.一元二次方程 3 x2+x-10=0的两个根是x1= -2 ,x2=5/3, 那么二次函数y= 3 x2+x-10与x轴的交点坐标是_____.归纳:一元二次方程ax2+bx+c=0的两个根为x1,x2 ,则抛物线 y=ax2+bx+c与x轴的交点坐标是(x1,0),(x2,0)(2.5,0), (-1,0)(-2,0) (5/3,0)有牛刀小试1.不与x轴相交的抛物线是( )
A. y = 2x2 – 3 B. y=-2 x2 + 3
C. y= -x2 – 3x D. y=-2(x+1)2 -3 2.若抛物线 y = ax2+bx+c= 0,当 a>0,c<0时,图象与x轴交点情况是( )
A. 无交点 B. 只有一个交点
C. 有两个交点 D. 不能确定DC 3. 如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m=___,此时抛物线 y=x2-2x+m与x轴有__个交点. 4.已知抛物线 y=x2 – 8x + c的顶点在 x轴上,则 c =__.1116 5.若抛物线 y=x2 + bx+ c 的顶点在第一象限,则方程 x2 + bx+ c =0 的根的情况是_____.b2-4ac < 0 无实数根 6.抛物线 y=2x2-3x-5 与y轴交于点____,与x轴交于点 . 7.一元二次方程 3 x2+x-10=0的两个根是x1=-2 ,x2=5/3,那么二次函数 y= 3 x2+x-10与x轴的交点坐标是________.(0,-5)(5/2,0) (-1,0)(-2,0) (5/3,0) 8.已知抛物线y = ax2+bx+c的图象如图,则关于x的方程ax2 + bx + c-3 = 0根的情况是( )
A. 有两个不相等的实数根
B. 有两个异号绝对值相等的实数根
C. 有两个相等的实数根
D. 没有实数根xA1.3. 9.根据下列表格的对应值:
判断方程 ax2+bx+c =0 (a≠0,a,b,c为常数)一个解x的范围是( )
A. 3< x < 3.23 B. 3.23 < x < 3.24
C. 3.24 相交于点P(3,4m)。
(1)求这两个函数的关系式;
(2)当x取何值时,抛物线与直线相交,并求交点坐标。解:(1)因为点P(3,4m)在直线 上,所以 ,解得m=1
所以 ,P(3,4)。因为点P(3,4)在抛物线 上,所以有4=18-24+k+8 解得 k=2
所以
(2)依题意,得
解这个方程组,得
所以抛物线与直线的两个交点坐标分别是(3,4),(1.5,2.5)。用图像法求一元二次方程的近似解例方法: (1)先作出图象;
(2)写出交点的坐标;
(-1.3、0)、(2.3、0)
(3)得出方程的解.
x =-1.3,x =2.3。利用二次函数的图象求方程x2-x-3=0的实数根(精确到0.1). xy用你学过的一元二次方程的解法来解,
准确答案是什么?【例1】你能利用二次函数的图象估计一元二次方程
的两根吗?其基本步骤是什么?解:1、画出函数的图象。2、由图象可知方程有两个根,一个根在-5和-4之间,一个在2和3之间。3、探求其解的十分位。∴ 方程的两个近似根为x1≈-4.3,x2≈2.3。基本步骤:
1、画出函数的图象;
2、根据图象确定抛物线
与x轴的交点分别在哪两
个相邻的整数之间;
3、利用计算器探索其解
的十分位数字,从而确定
方程的近似根。试一试CA(4)已知二次函数y=ax+bx+c的图象如图所示,则
一元二次方程ax+bx+c=0的解是 .
XY0522(5)若抛物线y=ax2+bx+c,当 a>0,c<0时,图象与x轴交点情况是( )
A 无交点 B 只有一个交点
C 有两个交点 D不能确定CX1=0,x2=5(6)如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m=____,此时抛物线 y=x2-2x+m与x轴有____个交点.(7)已知抛物线 y=x2 – 8x +c的顶点在 x轴上,则c=____.1116 (8)一元二次方程 3 x2+x-10=0的两个根是x1= -2 ,x2=5/3, 那么二次函数y= 3 x2+x-10与x轴的交点坐标是____.(-2、0)(5/3、0)(9)根据下列表格的对应值:
判断方程ax2+bx+c=0 (a≠0,a,b,c为常数)一个解x的范围是( )
A 3< X < 3.23 B 3.23 < X < 3.24
C 3.24则m的取值范围是 。2、如果关于x的方程x2-2x+m=0有两个相等
的实数根,此时抛物线y=x2-2x+m与x轴有
个交点。3、抛物线y=x2-kx+k-2与x轴交点个数为( )
A、0个 B、1个 C、2个 D、无法确定亮出你的风采4、已知二次函数y=-x2+2x+k+2
与x轴的公共点有两个,
(1)求k的取值范围;
(2)当k=1时,求抛物线与
x轴的公共点A和B的坐标及顶点C的坐标;
(3)观察图象,当x取何值时,y=0,y>0,y<0?
(4)在x轴下方的抛物线上是否存在点P,使S⊿ABP是S⊿ABC的一半,若存在,求出P点的坐标,若不存在,请说明理由.亮出你的风采yx亮出你的风采5、已知二次函数y=x2-mx-m2
(1)求证:对于任意实数m,该二次函数的图像与x轴总有公共点;
(2)该二次函数的图像与x轴有两个公共点A、B,且A点坐标为(1、0),求B点坐标。
2、你能否用类比的方法猜想二次函数y=ax2+bx+c与
一元二次方程ax2+bx+c=0的关系?
以 40 m /s的速度将小球沿与地面成 30°角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气阻力,球的飞行高度 h (单位:m)与飞行时间 t (单位:s)之间具有关系:h= 20 t – 5 t 2
考虑下列问题:
(1)球的飞行高度能否达到 15 m? 若能,需要多少时间?
(2)球的飞行高度能否达到 20 m? 若能,需要多少时间?
(3)球的飞行高度能否达到 20.5 m?为什么?
(4)球从飞出到落地要用多少时间?解:(1)当 h = 15 时,20 t – 5 t 2 = 15t 2 - 4 t +3 = 0t 1 = 1,t 2 = 3当球飞行 1s 和 3s 时,它的高度为 15m .1s3s15 m 以 40 m /s的速度将小球沿与地面成 30°角的方向击出时,
球的飞行路线是一条抛物线,如果不考虑空气阻力,球
的飞行高度 h (单位:m)与飞行时间 t (单位:s)之间具有关系:h= 20 t – 5 t 2
考虑下列问题:
(1)球的飞行高度能否达到 15 m? 若能,需要多少时间?
(2)当 h = 20 时,20 t – 5 t 2 = 20t 2 - 4 t +4 = 0t 1 = t 2 = 2当球飞行 2s 时,它的高度为 20m .2s20 m以 40 m /s的速度将小球沿与地面成 30°角的方向击出时,
球的飞行路线是一条抛物线,如果不考虑空气阻力,球的
飞行高度 h (单位:m)与飞行时间 t (单位:s)之间具有关系:h= 20 t – 5 t 2
考虑下列问题:(2)球的飞行高度能否达到 20 m? 若能,需要多少时间?
(3)当 h = 20.5 时,20 t – 5 t 2 = 20.5t 2 - 4 t +4.1 = 0因为(-4)2-4×4.1 < 0 ,所以方程无实根。
球的飞行高度达不到 20.5 m.20.5 m以 40 m /s的速度将小球沿与地面成 30°角的方向击出时,球的飞行路线
是一条抛物线,如果不考虑空气阻力,球的飞行高度 h (单位:m)与飞行
时间 t (单位:s)之间具有关系:h= 20 t – 5 t 2
考虑下列问题:(3)球的飞行高度能否达到 20.5 m?为什么?
(4)当 h = 0 时,20 t – 5 t 2 = 0t 2 - 4 t = 0t 1 = 0,t 2 = 4当球飞行 0s 和 4s 时,它的高度为 0m ,即 0s时,球从地面飞出,4s 时球落回地面。0s4s0 m 以 40 m /s的速度将小球沿与地面成 30°角的方向击出时,球的飞行路线
是一条抛物线,如果不考虑空气阻力,球的飞行高度 h (单位:m)与飞行时
间 t (单位:s)之间具有关系:h= 20 t – 5 t 2
考虑下列问题:(4)球从飞出到落地要用多少时间?
从上面发现,二次函数y=ax2+bx+c何时为一元二次方程?一般地,当y取定值时,二次函数为一元二次方程。如:y=5时,则5=ax2+bx+c就是一个一元二次方程。
自由讨论例如,已知二次函数y=-X2+4x的值为3,求自变量x的值.就是求方程3=-X2+4x的解,例如,解方程X2-4x+3=0就是已知二次函数y=X2-4x+3的值为0,求自变量x的值.已知二次函数,求自变量的值解一元二次方程的根二次函数与一元二次方程的关系(1)1、二次函数y = x2+x-2 , y = x2 - 6x +9 , y = x2 – x+ 1的图象如图所示。(1).每个图象与x轴有几个交点?
(2).一元二次方程? x2+x-2=0 , x2 - 6x +9=0有几个根?
验证一下一元二次方程x2 – x+ 1 =0有根吗?
(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与
一元二次方程ax2+bx+c=0的根有什么关系?答:2个,1个,0个边观察边思考(3),二次函数y=ax2+bx+c的图象和x轴交点的坐标与 一元二次方程ax2+bx+c=0的根有什么关系?(-2,0),(1,0)x1=-2,x2=1(3,0)x1=x2=3无交点无实根 抛物线y=ax2+bx+c与x轴交点的横坐标是方程ax2+bx+c =0的根。归纳一元二次方程ax2+bx+c=0的两个根为x1,x2 ,则抛物线 y=ax2+bx+c与x轴的交点坐标是(x1,0),(x2,0)
下列二次函数的图象与 x 轴有交点吗? 若有,求出交点坐标.
(1) y = 2x2+x-3
(2) y = 4x2 -4x +1
(3) y = x2 – x+ 1令 y= 0,解一元二次方程的根(1) y = 2x2+x-3解:当 y = 0 时,2x2+x-3 = 0(2x+3)(x-1) = 0x 1 = ,x 2 = 1 所以与 x 轴有交点,有两个交点。y =a(x-x1)(x- x 2)二次函数的交点式 (2) y = 4x2 -4x +1解:当 y = 0 时,4x2 -4x +1 = 0(2x-1)2 = 0x 1 = x 2 = 所以与 x 轴有一个交点。(3) y = x2 – x+ 1解:当 y = 0 时,x2 – x+ 1 = 0 所以与 x 轴没有交点。因为(-1)2-4×1×1 = -3 < 0确定二次函数图象与 x 轴的位置关系解一元二次方程的根二次函数与一元二次方程的关系(2)有两个根
有一个根(两个相同的根)
没有根有两个交点
有一个交点
没有交点b2 – 4ac > 0b2 – 4ac = 0b2 – 4ac < 0二次函数 y=ax2+bx+c 的图象和x轴交点的三种情况与一元二次方程根的关系ax2+bx+c = 0 的根 y=ax2+bx+c 的图象与x轴 若抛物线 y=ax2+bx+c 与 x 轴有交点,则________________ 。b2 – 4ac ≥ 0△>0△=0△<0oxy△ = b2 – 4ac△>0△=0△<0oxy△ = b2 – 4ac 二次函数 y=ax2+bx+c 的图象和x轴交点的三种情况与一元二次方程根的关系:有两个交点有两个不相等的实数根只有一个交点有两个相等的实数根没有交点没有实数根b2 – 4ac > 0b2 – 4ac = 0b2 – 4ac < 0与x轴有两个不
同的交点
(x1,0)
(x2,0)有两个不同的解x=x1,x=x2b2-4ac>0与x轴有唯一个
交点有两个相等的解
x1=x2=b2-4ac=0与x轴没有
交点没有实数根b2-4ac<02.抛物线y=2x2-3x-5 与x轴有无交点?若无说出理由,若有求出交点坐标?1.一元二次方程 3 x2+x-10=0的两个根是x1= -2 ,x2=5/3, 那么二次函数y= 3 x2+x-10与x轴的交点坐标是_____.归纳:一元二次方程ax2+bx+c=0的两个根为x1,x2 ,则抛物线 y=ax2+bx+c与x轴的交点坐标是(x1,0),(x2,0)(2.5,0), (-1,0)(-2,0) (5/3,0)有牛刀小试1.不与x轴相交的抛物线是( )
A. y = 2x2 – 3 B. y=-2 x2 + 3
C. y= -x2 – 3x D. y=-2(x+1)2 -3 2.若抛物线 y = ax2+bx+c= 0,当 a>0,c<0时,图象与x轴交点情况是( )
A. 无交点 B. 只有一个交点
C. 有两个交点 D. 不能确定DC 3. 如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m=___,此时抛物线 y=x2-2x+m与x轴有__个交点. 4.已知抛物线 y=x2 – 8x + c的顶点在 x轴上,则 c =__.1116 5.若抛物线 y=x2 + bx+ c 的顶点在第一象限,则方程 x2 + bx+ c =0 的根的情况是_____.b2-4ac < 0 无实数根 6.抛物线 y=2x2-3x-5 与y轴交于点____,与x轴交于点 . 7.一元二次方程 3 x2+x-10=0的两个根是x1=-2 ,x2=5/3,那么二次函数 y= 3 x2+x-10与x轴的交点坐标是________.(0,-5)(5/2,0) (-1,0)(-2,0) (5/3,0) 8.已知抛物线y = ax2+bx+c的图象如图,则关于x的方程ax2 + bx + c-3 = 0根的情况是( )
A. 有两个不相等的实数根
B. 有两个异号绝对值相等的实数根
C. 有两个相等的实数根
D. 没有实数根xA1.3. 9.根据下列表格的对应值:
判断方程 ax2+bx+c =0 (a≠0,a,b,c为常数)一个解x的范围是( )
A. 3< x < 3.23 B. 3.23 < x < 3.24
C. 3.24
(1)求这两个函数的关系式;
(2)当x取何值时,抛物线与直线相交,并求交点坐标。解:(1)因为点P(3,4m)在直线 上,所以 ,解得m=1
所以 ,P(3,4)。因为点P(3,4)在抛物线 上,所以有4=18-24+k+8 解得 k=2
所以
(2)依题意,得
解这个方程组,得
所以抛物线与直线的两个交点坐标分别是(3,4),(1.5,2.5)。用图像法求一元二次方程的近似解例方法: (1)先作出图象;
(2)写出交点的坐标;
(-1.3、0)、(2.3、0)
(3)得出方程的解.
x =-1.3,x =2.3。利用二次函数的图象求方程x2-x-3=0的实数根(精确到0.1). xy用你学过的一元二次方程的解法来解,
准确答案是什么?【例1】你能利用二次函数的图象估计一元二次方程
的两根吗?其基本步骤是什么?解:1、画出函数的图象。2、由图象可知方程有两个根,一个根在-5和-4之间,一个在2和3之间。3、探求其解的十分位。∴ 方程的两个近似根为x1≈-4.3,x2≈2.3。基本步骤:
1、画出函数的图象;
2、根据图象确定抛物线
与x轴的交点分别在哪两
个相邻的整数之间;
3、利用计算器探索其解
的十分位数字,从而确定
方程的近似根。试一试CA(4)已知二次函数y=ax+bx+c的图象如图所示,则
一元二次方程ax+bx+c=0的解是 .
XY0522(5)若抛物线y=ax2+bx+c,当 a>0,c<0时,图象与x轴交点情况是( )
A 无交点 B 只有一个交点
C 有两个交点 D不能确定CX1=0,x2=5(6)如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m=____,此时抛物线 y=x2-2x+m与x轴有____个交点.(7)已知抛物线 y=x2 – 8x +c的顶点在 x轴上,则c=____.1116 (8)一元二次方程 3 x2+x-10=0的两个根是x1= -2 ,x2=5/3, 那么二次函数y= 3 x2+x-10与x轴的交点坐标是____.(-2、0)(5/3、0)(9)根据下列表格的对应值:
判断方程ax2+bx+c=0 (a≠0,a,b,c为常数)一个解x的范围是( )
A 3< X < 3.23 B 3.23 < X < 3.24
C 3.24
的实数根,此时抛物线y=x2-2x+m与x轴有
个交点。3、抛物线y=x2-kx+k-2与x轴交点个数为( )
A、0个 B、1个 C、2个 D、无法确定亮出你的风采4、已知二次函数y=-x2+2x+k+2
与x轴的公共点有两个,
(1)求k的取值范围;
(2)当k=1时,求抛物线与
x轴的公共点A和B的坐标及顶点C的坐标;
(3)观察图象,当x取何值时,y=0,y>0,y<0?
(4)在x轴下方的抛物线上是否存在点P,使S⊿ABP是S⊿ABC的一半,若存在,求出P点的坐标,若不存在,请说明理由.亮出你的风采yx亮出你的风采5、已知二次函数y=x2-mx-m2
(1)求证:对于任意实数m,该二次函数的图像与x轴总有公共点;
(2)该二次函数的图像与x轴有两个公共点A、B,且A点坐标为(1、0),求B点坐标。
