4.1 函数和它的表示法(1)同步练习
文档属性
| 名称 | 4.1 函数和它的表示法(1)同步练习 |

|
|
| 格式 | doc | ||
| 文件大小 | 544.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-02 15:06:07 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
4.1 函数和它的表示法(1)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.在某一变化过程中,取值 发生变化的量称为变量,取值固定不变的量称为常量或常数.
①常量与变量必须存在于同一个变化过程中, ( http: / / www.21cnjy.com )判断一个量是常量还是变量,需要看两个方面:一是它是否在一个变化过程中;二是看它在这个变化过程中的取值情况是否发生变化;
②常量和变量是相对于变化过程而言的.可以互相转化;
③不要认为字母就是变量,例如π是常量. 【来源:21cnj*y.co*m】
2.一般地,如果变量y随着变量x 而变化,并且对于x 取的每一个值,y都有唯一的一个值与它对应,那么称y是x的函数,记作y=f(x).【出处:21教育名师】
对于函数概念的理解:①有两个变量;②一个变 ( http: / / www.21cnjy.com )量的数值随着另一个变量的数值的变化而发生变化;③对于自变量的每一个确定的值,函数值有且只有一个值与之对应,即单对应.
3.对于自变量x取的每一个值a,因变量y 的对应值称为函数值,记为 f(a) .
①当已知函数解析式时,求函数值就是求 ( http: / / www.21cnjy.com )代数式的值;当已知函数解析式,给出函数值时,求相应的自变量的值就是解方程;
②当自变量确定时,函数值是唯一确定的.但当函数值唯一确定时,对应的自变量可以是多个.
4.自变量的取值范围必须 ( http: / / www.21cnjy.com )使含有自变量的表达式都有意义.
①当表达式的分母不含有自变量时,自变量取全体实数.例如y=2x+13中的x.
②当表达式的分母中含有自变量时,自变量取值要使分母不为零.例如y=x+2x-1.
③当函数的表达式是偶次根式时,自变量的取值范围必须使被开方数不小于零.
④对于实际问题中的函数关系式,自变量的取值除必须使表达式有意义外,还要保证实际问题有意义.
基础知识和能力拓展精练
一、选择题
1.在圆的面积公式S=πr2中,是常量的是( )
A. S B. π C. R D. S和r
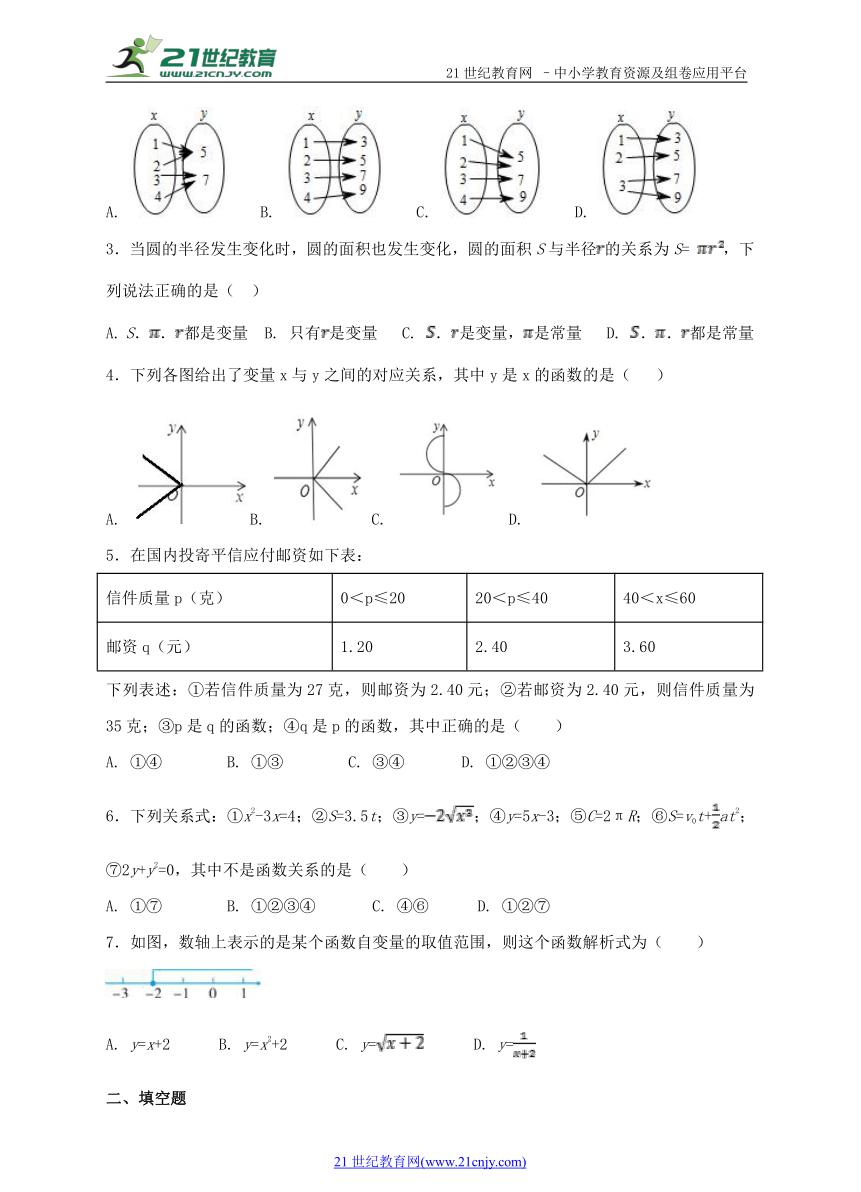
2.下列关于变量x,y的关系,其中y不是x的函数的是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
3.当圆的半径发生变化时,圆的面积也发生变化,圆的面积S与半径的关系为S= ,下列说法正确的是( )
A. S..都是变量 B. 只有是变量 C. .是变量,是常量 D. ..都是常量
4.下列各图给出了变量x与y之间的对应关系,其中y是x的函数的是( )
A. ( http: / / www.21cnjy.com )B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
5.在国内投寄平信应付邮资如下表:
信件质量p(克) 0<p≤20 20<p≤40 40<x≤60
邮资q(元) 1.20 2.40 3.60
下列表述:①若信件质量为27克,则邮资 ( http: / / www.21cnjy.com )为2.40元;②若邮资为2.40元,则信件质量为35克;③p是q的函数;④q是p的函数,其中正确的是( )
A. ①④ B. ①③ C. ③④ D. ①②③④
6.下列关系式:①x2-3x=4;②S=3.5t;③y=;④y=5x-3;⑤C=2πR;⑥S=v0t+at2;⑦2y+y2=0,其中不是函数关系的是( )
A. ①⑦ B. ①②③④ C. ④⑥ D. ①②⑦
7.如图,数轴上表示的是某个函数自变量的取值范围,则这个函数解析式为( )
( http: / / www.21cnjy.com )
A. y=x+2 B. y=x2+2 C. y= D. y=
二、填空题
8.如图是济南市8月2日的气温随时间变化的图象,根据图象可知:在这一天中,气温T(℃)____(填“是”或“不是”)时间t(时)的函数.
( http: / / www.21cnjy.com )
9.完成以下问题:
(1)某人持续以a米/分钟的速度t分钟内跑了s米,其中常量是_______________ ,变量是_______________;
(2)在t分钟内,不同的人以不同的速度a米/分钟跑了s米,其中常量是______________,变量是 _______________;
(3)s米的路程不同的人以不同的速度a米/分钟各需跑t分钟,其中常量是 ____________,变量是 _______________;
(4)根据以上叙述,写一句关于常量与变量的结论: _________________________.
10.在函数中,自变量的取值范围是__________.
11.如图所示,梯形的上底长是厘米,下底长是厘米,当梯形的高由大变小时,梯形的面积也随之发生变化.21*cnjy*com
( http: / / www.21cnjy.com )
()在这个变化过程中,自变量是__________,因变量是__________.
()梯形的面积与高(厘米)之间的关系式为__________.
()当梯形的高由厘米变化到厘米时,梯形的面积由__________变化到__________.
12.下列变量间的关系是函数关系的有_____________________(填序号)
①正方形的周长与边长;②圆的面积与半径;
③;④商场中某种商品的单价为a元,销售总额与销售数量
三、解答题
13.写出下列各问题中的关系式中的常量与变量:
(1)时针旋转一周内,旋转的角度n(度)与旋转所需要的时间t(分)之间的关系式n=6t;
(2)一辆汽车以40千米/时的速度向前匀速直线行驶时,汽车行驶的路程S(千米)与行驶时间t(时)之间的关系式s=40t。【来源:21·世纪·教育·网】
14.求下列函数中自变量的取值范围.
;
;
;
;
.
15.某影碟出租店开设两种租 ( http: / / www.21cnjy.com )碟方式:一种是零星租碟,每张收费 1 元;另一种是会员卡租碟,办 卡费每月 12 元,租碟费每张 0.4 元.小彬经常来该店租碟,且每月租碟数量为 x 张.21·世纪*教育网
(1) 写出零星租碟方式应付金额 y1 (元)与租碟数量 x(张)之间的关系式;
(2) 写出会员卡租碟方式应付金额 y2 (元)与租碟数量 x(张)之间的关系;
(3) 当 x = 22 张时,小彬选取哪种租碟方式更合算
16.青春期男、女生身高变化情况不尽相同,如图是小军和小蕊青春期身高的变化情况.
( http: / / www.21cnjy.com )
(1)如图反映了哪两个变量之间的关系 自变量是什么 因变量是什么
(2)A,B两点表示什么
(3)小蕊10岁时身高多少
17.下表是橘子的卖钱额随橘子卖出质量的变化表:
质量/千克 1 2 3 4 5 6 7 8 9
卖钱额/元 2 4 6 8 10 12 14 16 18
(1)在这个表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用x表示橘子的卖出质量,y表示卖钱额,按表中给出的关系,用一个式子把y与x之间的关系表示出来;21世纪教育网版权所有
(3)当橘子卖出50千克时,预测卖钱额是多少?
18.如图, 的底边BC的长是12cm,当顶点A在BC的垂线PD上由点D向上移动时,三角形的面积起了变化,21教育名师原创作品
(1)在这个变化的过程中,自变量是 ,因变量是 .
(2)如果AD为x(cm),面积为y(),可表示为y=
(3)当AD=BC时 , 的面积为
( http: / / www.21cnjy.com )
19.如图,长方形ABCD中,AB=4,BC=8.点P在AB上运动,设PB=x,图中阴影部分的面积为y.
( http: / / www.21cnjy.com )
(1)写出阴影部分的面积y与x之间的函数解析式和自变量x的取值范围;
(2)点P在什么位置时,阴影部分的面积等于20?
参考答案
1.B
【解析】S=πr2中,是常量的是π.
故选B.
点睛:常量是指不变化的量.
2.D
【解析】函数的定义:一般地,在一个 ( http: / / www.21cnjy.com )变化过程中有两个变量x、y,如果对于x在某一范围内的每一个确定的值,y都有唯一确定的值与它对应,那么就称y是x的函数.
D选项中,当x=3时,y有两个确定的值与之对应,不是唯一确定的,所以D选项y不是x的函数.
故选D.
点睛:对于函数概念的理解主要抓住以下三点:① ( http: / / www.21cnjy.com )有两个变量;②一个变量的每一个数值随着另一个变量的数值的变化而变化;③对于自变量每一个确定的值,函数有且只有一个值与之对应.www.21-cn-jy.com
3.C
【解析】在变化过程中,某量 ( http: / / www.21cnjy.com )若保持不变,则称之为常量;反之,则称之为变量.π是常数,约等于3.14,是不变的常数,所以它是常量;S和r是变化的量,故是变量,
故选C.
4.D
【解析】根据函数的意义可知:对于自变量x的任何值,y都有唯一的值与之相对应,只有选项D符合要求,故选D.21·cn·jy·com
5.A
【解析】①若信件质量为2 ( http: / / www.21cnjy.com )7克,则邮资为2.40元,故正确;②若邮资为2.40元,则信件质量在20克到40克之间,故错误;q是p的函数,所以③错误,④正确.
故选A.
6.A
【解析】函数是指两个变量之间的关系,而 ( http: / / www.21cnjy.com )①⑦只有一个变量,故①⑦不是函数;②③④⑤都有两个变量,并且给等号右边的变量一个确定的值,等号左边的变量都只有唯一的值与之对应,所以②③④⑤都是函数;⑥是以后将要学习的一个物理公式,对于一个确定的运动过程而言,v0和a都是不变的,只有S和t两个变量,并且满足一一对应,故⑥也是函数,
故选A.
7.C
【解析】解:观察数轴可知:x≥-2.
A、y=x+2,x为任意实数,故错误;
B、y=x2+2,x为任意实数,故错误;
C、,x+2≥0,即x≥-2,故正确;
D、y=,x+2≠0,即x≠-2,故错误。
故选C.
8.是
【解析】由题意得,气温T(℃)是时间t(时)的函数.
9. (1)a;t,s;(2)t;a ( http: / / www.21cnjy.com ),s;(3)s;t,a;(4)在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量. 21cnjy.com
【解析】(1)某人持续以a米/分钟 ( http: / / www.21cnjy.com )的速度t分钟内跑了s米,其中常量是a,变量是t,s;(2)在t分钟内,不同的人以不同的速度a米/分钟跑了s米,其中常量是t,变量是a,s;(3)s米的路程不同的人以不同的速度a米/分钟各需跑t分钟,其中常量是s,变量是t,a;(4)在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量.
故答案为(1).a;t,s;(2).t; ( http: / / www.21cnjy.com )a,s;(3).s;t,a;(4).在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量.2·1·c·n·j·y
10.
【解析】根据分式的分母不等于零,得,解得.
故答案为:.
11. 梯形的高 梯形的面积 90 9
【解析】(1)自变量是梯形的高,因变量是梯形的面积;
(2)梯形的面积y(cm )与高x(cm)之间的关系式为:y=(5+13)x×=9x;
(3)当梯形的高是l0cm时,y=9×10=90,
当梯形的高是l0cm时,y=9×1=9,
梯形的面积由90cm 变化到9cm .故答案为:梯形的高, 梯形的面积, y=9x, 90, 9.
12.①②④.
【解析】在一个变化过程中,有两个变量 ( http: / / www.21cnjy.com )x和y,对于x的每一个确定值,y都有唯一的值与之对应,则称y是x的函数,在③中,当x取一个值时,对应的y值有两个,故不是函数,
故答案为:①②④.
13.(1)常量:6;变量:n,t;(2)常量:40;变量:s,t。
【解析】试题分析:根据在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常.据此判断即可.www-2-1-cnjy-com
解:(1)∵n=6t,∴常量是6,变量是n,t;
(2)∵s=40t,∴常量是40,变量是s,t.
14.(1)全体实数;(2);(3);(4);(5)
【解析】分析:根据当函数表达式是整式时 ( http: / / www.21cnjy.com ),自变量可取全体实数,当函数表达式是分式时,考虑分式的分母不能为0,当函数表达式是二次根式时,被开方数非负进行解答.
本题解析: 的取值范围为全体实数;
解不等式,得,故x的取值范围为;
解不等式,得,故x的取值范围为;
解不等式,得,故x的取值范围为;
解不等式组得,故x的取值范围为.
点睛:本题考查的是函数自变量的 ( http: / / www.21cnjy.com )取值范围的确定,函数自变量的范围一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数为非负数.【版权所有:21教育】
15.(1) y1 = x;(2) y2 = 0.4x + 12;(3)会员卡方式租碟更合算,理由见解析
【解析】试题分析:
(1)根据题中所给数量关系列出y1与x间的函数关系式即可;
(2)根据题中所给数量关系列出y2与x间的函数关系式即可;
(3)把x=22分别代入(1)和(2)中所得函数关系式分别计算出对应的y1和y2,并比较两者的大小关系即可得出结论.21*cnjy*com
试题解析:
(1)由题意可得:y1=x;
(2)由题意可得:y2=0.4x+12;
(3)当x=22时,y1=22(元);
当x=22时,y2=0.4×22+12=20.8(元);
∵22>20.8,
∴会员卡方式租碟更合算.
16.(1)反映了身高和年龄的关系,自 ( http: / / www.21cnjy.com )变量是年龄,因变量是身高;(2)A点表示小军和小蕊在11岁半时身高都是143 cm,B点表示小军和小蕊在15岁时身高都是156 cm;(3)127cm
【解析】试题分析:(1)根据横坐标与纵坐标表示的量解答;
(2)根据交点的纵坐标相等可知二人身高相等;
(3)根据平面直角坐标系确定横坐标为10时的身高值即可.
试题解析:
解:(1)反映了身高随年龄的变化而变化的关系,自变量是年龄,因变量是身高;
(2)A点表示小军和小蕊在11岁半时身高都是143厘米,B点表示小军和小蕊在15岁时身高都是156厘米;
(3)小蕊10岁时身高127厘米.
( http: / / www.21cnjy.com )
点睛:本题考查利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的解决.
17.(1)质量和卖钱额都是变量,质量是自变量;(2)y=2x;(3)100元.
【解析】试题分析: 根据表格的第一列确定变量,再结合自变量及因变量的定义确定自变量与因变量;
(2)根据表格可知销售单价,由“单价×数量=总价”即可求出y与x的关系;
(3)将x=50代入(2)中的关系式,即可求得卖出50千克时的卖钱额.
试题解析:
(1) 卖钱额是随卖出质量的变化而变化,所以质量和卖钱额都是变量,质量是自变量,卖钱额是因变量;
(2) y与x之间的关系: y=2x;
(3)当时,
即当橘子卖出50千克时,预测卖钱额是100元.
18.(1)△ABC是底边BC边上的高AD的长,△ABC的面积;(2);(3).
【解析】试题分析:(1)根据函数的概念即可得;
(2)根据三角形的面积公式,可得三角形的面积与高的关系,可得答案.
(3)由面积公式即可得到.
试题解析:(1)自变量是△ABC是底边BC边上的高AD的长,因变量是△ABC的面积;
(2)如果AD为x(cm),面积为y (),可表示为;
(3)当AD=BC时,△ABC的面积为.
( http: / / www.21cnjy.com )
19.(1)阴影部分的面积为:y=32-4x(0<x≤4);(2)PB=3
【解析】试题分析:(1)根据梯形的面积公式得出y与x的函数关系式即可;
(2)利用(1)中所求得出y=20,求出x即可得出答案.21教育网
试题解析:(1)设PB=x,长方形ABCD中,AB=4,BC=8,
则图中阴影部分的面积为:y=(4-x+4)×8=32-4x(0≤x≤4).
(2)当y=20时,20=32-4x,解得x=3,即PB=3.2-1-c-n-j-y
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.1 函数和它的表示法(1)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.在某一变化过程中,取值 发生变化的量称为变量,取值固定不变的量称为常量或常数.
①常量与变量必须存在于同一个变化过程中, ( http: / / www.21cnjy.com )判断一个量是常量还是变量,需要看两个方面:一是它是否在一个变化过程中;二是看它在这个变化过程中的取值情况是否发生变化;
②常量和变量是相对于变化过程而言的.可以互相转化;
③不要认为字母就是变量,例如π是常量. 【来源:21cnj*y.co*m】
2.一般地,如果变量y随着变量x 而变化,并且对于x 取的每一个值,y都有唯一的一个值与它对应,那么称y是x的函数,记作y=f(x).【出处:21教育名师】
对于函数概念的理解:①有两个变量;②一个变 ( http: / / www.21cnjy.com )量的数值随着另一个变量的数值的变化而发生变化;③对于自变量的每一个确定的值,函数值有且只有一个值与之对应,即单对应.
3.对于自变量x取的每一个值a,因变量y 的对应值称为函数值,记为 f(a) .
①当已知函数解析式时,求函数值就是求 ( http: / / www.21cnjy.com )代数式的值;当已知函数解析式,给出函数值时,求相应的自变量的值就是解方程;
②当自变量确定时,函数值是唯一确定的.但当函数值唯一确定时,对应的自变量可以是多个.
4.自变量的取值范围必须 ( http: / / www.21cnjy.com )使含有自变量的表达式都有意义.
①当表达式的分母不含有自变量时,自变量取全体实数.例如y=2x+13中的x.
②当表达式的分母中含有自变量时,自变量取值要使分母不为零.例如y=x+2x-1.
③当函数的表达式是偶次根式时,自变量的取值范围必须使被开方数不小于零.
④对于实际问题中的函数关系式,自变量的取值除必须使表达式有意义外,还要保证实际问题有意义.
基础知识和能力拓展精练
一、选择题
1.在圆的面积公式S=πr2中,是常量的是( )
A. S B. π C. R D. S和r
2.下列关于变量x,y的关系,其中y不是x的函数的是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
3.当圆的半径发生变化时,圆的面积也发生变化,圆的面积S与半径的关系为S= ,下列说法正确的是( )
A. S..都是变量 B. 只有是变量 C. .是变量,是常量 D. ..都是常量
4.下列各图给出了变量x与y之间的对应关系,其中y是x的函数的是( )
A. ( http: / / www.21cnjy.com )B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
5.在国内投寄平信应付邮资如下表:
信件质量p(克) 0<p≤20 20<p≤40 40<x≤60
邮资q(元) 1.20 2.40 3.60
下列表述:①若信件质量为27克,则邮资 ( http: / / www.21cnjy.com )为2.40元;②若邮资为2.40元,则信件质量为35克;③p是q的函数;④q是p的函数,其中正确的是( )
A. ①④ B. ①③ C. ③④ D. ①②③④
6.下列关系式:①x2-3x=4;②S=3.5t;③y=;④y=5x-3;⑤C=2πR;⑥S=v0t+at2;⑦2y+y2=0,其中不是函数关系的是( )
A. ①⑦ B. ①②③④ C. ④⑥ D. ①②⑦
7.如图,数轴上表示的是某个函数自变量的取值范围,则这个函数解析式为( )
( http: / / www.21cnjy.com )
A. y=x+2 B. y=x2+2 C. y= D. y=
二、填空题
8.如图是济南市8月2日的气温随时间变化的图象,根据图象可知:在这一天中,气温T(℃)____(填“是”或“不是”)时间t(时)的函数.
( http: / / www.21cnjy.com )
9.完成以下问题:
(1)某人持续以a米/分钟的速度t分钟内跑了s米,其中常量是_______________ ,变量是_______________;
(2)在t分钟内,不同的人以不同的速度a米/分钟跑了s米,其中常量是______________,变量是 _______________;
(3)s米的路程不同的人以不同的速度a米/分钟各需跑t分钟,其中常量是 ____________,变量是 _______________;
(4)根据以上叙述,写一句关于常量与变量的结论: _________________________.
10.在函数中,自变量的取值范围是__________.
11.如图所示,梯形的上底长是厘米,下底长是厘米,当梯形的高由大变小时,梯形的面积也随之发生变化.21*cnjy*com
( http: / / www.21cnjy.com )
()在这个变化过程中,自变量是__________,因变量是__________.
()梯形的面积与高(厘米)之间的关系式为__________.
()当梯形的高由厘米变化到厘米时,梯形的面积由__________变化到__________.
12.下列变量间的关系是函数关系的有_____________________(填序号)
①正方形的周长与边长;②圆的面积与半径;
③;④商场中某种商品的单价为a元,销售总额与销售数量
三、解答题
13.写出下列各问题中的关系式中的常量与变量:
(1)时针旋转一周内,旋转的角度n(度)与旋转所需要的时间t(分)之间的关系式n=6t;
(2)一辆汽车以40千米/时的速度向前匀速直线行驶时,汽车行驶的路程S(千米)与行驶时间t(时)之间的关系式s=40t。【来源:21·世纪·教育·网】
14.求下列函数中自变量的取值范围.
;
;
;
;
.
15.某影碟出租店开设两种租 ( http: / / www.21cnjy.com )碟方式:一种是零星租碟,每张收费 1 元;另一种是会员卡租碟,办 卡费每月 12 元,租碟费每张 0.4 元.小彬经常来该店租碟,且每月租碟数量为 x 张.21·世纪*教育网
(1) 写出零星租碟方式应付金额 y1 (元)与租碟数量 x(张)之间的关系式;
(2) 写出会员卡租碟方式应付金额 y2 (元)与租碟数量 x(张)之间的关系;
(3) 当 x = 22 张时,小彬选取哪种租碟方式更合算
16.青春期男、女生身高变化情况不尽相同,如图是小军和小蕊青春期身高的变化情况.
( http: / / www.21cnjy.com )
(1)如图反映了哪两个变量之间的关系 自变量是什么 因变量是什么
(2)A,B两点表示什么
(3)小蕊10岁时身高多少
17.下表是橘子的卖钱额随橘子卖出质量的变化表:
质量/千克 1 2 3 4 5 6 7 8 9
卖钱额/元 2 4 6 8 10 12 14 16 18
(1)在这个表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用x表示橘子的卖出质量,y表示卖钱额,按表中给出的关系,用一个式子把y与x之间的关系表示出来;21世纪教育网版权所有
(3)当橘子卖出50千克时,预测卖钱额是多少?
18.如图, 的底边BC的长是12cm,当顶点A在BC的垂线PD上由点D向上移动时,三角形的面积起了变化,21教育名师原创作品
(1)在这个变化的过程中,自变量是 ,因变量是 .
(2)如果AD为x(cm),面积为y(),可表示为y=
(3)当AD=BC时 , 的面积为
( http: / / www.21cnjy.com )
19.如图,长方形ABCD中,AB=4,BC=8.点P在AB上运动,设PB=x,图中阴影部分的面积为y.
( http: / / www.21cnjy.com )
(1)写出阴影部分的面积y与x之间的函数解析式和自变量x的取值范围;
(2)点P在什么位置时,阴影部分的面积等于20?
参考答案
1.B
【解析】S=πr2中,是常量的是π.
故选B.
点睛:常量是指不变化的量.
2.D
【解析】函数的定义:一般地,在一个 ( http: / / www.21cnjy.com )变化过程中有两个变量x、y,如果对于x在某一范围内的每一个确定的值,y都有唯一确定的值与它对应,那么就称y是x的函数.
D选项中,当x=3时,y有两个确定的值与之对应,不是唯一确定的,所以D选项y不是x的函数.
故选D.
点睛:对于函数概念的理解主要抓住以下三点:① ( http: / / www.21cnjy.com )有两个变量;②一个变量的每一个数值随着另一个变量的数值的变化而变化;③对于自变量每一个确定的值,函数有且只有一个值与之对应.www.21-cn-jy.com
3.C
【解析】在变化过程中,某量 ( http: / / www.21cnjy.com )若保持不变,则称之为常量;反之,则称之为变量.π是常数,约等于3.14,是不变的常数,所以它是常量;S和r是变化的量,故是变量,
故选C.
4.D
【解析】根据函数的意义可知:对于自变量x的任何值,y都有唯一的值与之相对应,只有选项D符合要求,故选D.21·cn·jy·com
5.A
【解析】①若信件质量为2 ( http: / / www.21cnjy.com )7克,则邮资为2.40元,故正确;②若邮资为2.40元,则信件质量在20克到40克之间,故错误;q是p的函数,所以③错误,④正确.
故选A.
6.A
【解析】函数是指两个变量之间的关系,而 ( http: / / www.21cnjy.com )①⑦只有一个变量,故①⑦不是函数;②③④⑤都有两个变量,并且给等号右边的变量一个确定的值,等号左边的变量都只有唯一的值与之对应,所以②③④⑤都是函数;⑥是以后将要学习的一个物理公式,对于一个确定的运动过程而言,v0和a都是不变的,只有S和t两个变量,并且满足一一对应,故⑥也是函数,
故选A.
7.C
【解析】解:观察数轴可知:x≥-2.
A、y=x+2,x为任意实数,故错误;
B、y=x2+2,x为任意实数,故错误;
C、,x+2≥0,即x≥-2,故正确;
D、y=,x+2≠0,即x≠-2,故错误。
故选C.
8.是
【解析】由题意得,气温T(℃)是时间t(时)的函数.
9. (1)a;t,s;(2)t;a ( http: / / www.21cnjy.com ),s;(3)s;t,a;(4)在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量. 21cnjy.com
【解析】(1)某人持续以a米/分钟 ( http: / / www.21cnjy.com )的速度t分钟内跑了s米,其中常量是a,变量是t,s;(2)在t分钟内,不同的人以不同的速度a米/分钟跑了s米,其中常量是t,变量是a,s;(3)s米的路程不同的人以不同的速度a米/分钟各需跑t分钟,其中常量是s,变量是t,a;(4)在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量.
故答案为(1).a;t,s;(2).t; ( http: / / www.21cnjy.com )a,s;(3).s;t,a;(4).在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量.2·1·c·n·j·y
10.
【解析】根据分式的分母不等于零,得,解得.
故答案为:.
11. 梯形的高 梯形的面积 90 9
【解析】(1)自变量是梯形的高,因变量是梯形的面积;
(2)梯形的面积y(cm )与高x(cm)之间的关系式为:y=(5+13)x×=9x;
(3)当梯形的高是l0cm时,y=9×10=90,
当梯形的高是l0cm时,y=9×1=9,
梯形的面积由90cm 变化到9cm .故答案为:梯形的高, 梯形的面积, y=9x, 90, 9.
12.①②④.
【解析】在一个变化过程中,有两个变量 ( http: / / www.21cnjy.com )x和y,对于x的每一个确定值,y都有唯一的值与之对应,则称y是x的函数,在③中,当x取一个值时,对应的y值有两个,故不是函数,
故答案为:①②④.
13.(1)常量:6;变量:n,t;(2)常量:40;变量:s,t。
【解析】试题分析:根据在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常.据此判断即可.www-2-1-cnjy-com
解:(1)∵n=6t,∴常量是6,变量是n,t;
(2)∵s=40t,∴常量是40,变量是s,t.
14.(1)全体实数;(2);(3);(4);(5)
【解析】分析:根据当函数表达式是整式时 ( http: / / www.21cnjy.com ),自变量可取全体实数,当函数表达式是分式时,考虑分式的分母不能为0,当函数表达式是二次根式时,被开方数非负进行解答.
本题解析: 的取值范围为全体实数;
解不等式,得,故x的取值范围为;
解不等式,得,故x的取值范围为;
解不等式,得,故x的取值范围为;
解不等式组得,故x的取值范围为.
点睛:本题考查的是函数自变量的 ( http: / / www.21cnjy.com )取值范围的确定,函数自变量的范围一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数为非负数.【版权所有:21教育】
15.(1) y1 = x;(2) y2 = 0.4x + 12;(3)会员卡方式租碟更合算,理由见解析
【解析】试题分析:
(1)根据题中所给数量关系列出y1与x间的函数关系式即可;
(2)根据题中所给数量关系列出y2与x间的函数关系式即可;
(3)把x=22分别代入(1)和(2)中所得函数关系式分别计算出对应的y1和y2,并比较两者的大小关系即可得出结论.21*cnjy*com
试题解析:
(1)由题意可得:y1=x;
(2)由题意可得:y2=0.4x+12;
(3)当x=22时,y1=22(元);
当x=22时,y2=0.4×22+12=20.8(元);
∵22>20.8,
∴会员卡方式租碟更合算.
16.(1)反映了身高和年龄的关系,自 ( http: / / www.21cnjy.com )变量是年龄,因变量是身高;(2)A点表示小军和小蕊在11岁半时身高都是143 cm,B点表示小军和小蕊在15岁时身高都是156 cm;(3)127cm
【解析】试题分析:(1)根据横坐标与纵坐标表示的量解答;
(2)根据交点的纵坐标相等可知二人身高相等;
(3)根据平面直角坐标系确定横坐标为10时的身高值即可.
试题解析:
解:(1)反映了身高随年龄的变化而变化的关系,自变量是年龄,因变量是身高;
(2)A点表示小军和小蕊在11岁半时身高都是143厘米,B点表示小军和小蕊在15岁时身高都是156厘米;
(3)小蕊10岁时身高127厘米.
( http: / / www.21cnjy.com )
点睛:本题考查利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的解决.
17.(1)质量和卖钱额都是变量,质量是自变量;(2)y=2x;(3)100元.
【解析】试题分析: 根据表格的第一列确定变量,再结合自变量及因变量的定义确定自变量与因变量;
(2)根据表格可知销售单价,由“单价×数量=总价”即可求出y与x的关系;
(3)将x=50代入(2)中的关系式,即可求得卖出50千克时的卖钱额.
试题解析:
(1) 卖钱额是随卖出质量的变化而变化,所以质量和卖钱额都是变量,质量是自变量,卖钱额是因变量;
(2) y与x之间的关系: y=2x;
(3)当时,
即当橘子卖出50千克时,预测卖钱额是100元.
18.(1)△ABC是底边BC边上的高AD的长,△ABC的面积;(2);(3).
【解析】试题分析:(1)根据函数的概念即可得;
(2)根据三角形的面积公式,可得三角形的面积与高的关系,可得答案.
(3)由面积公式即可得到.
试题解析:(1)自变量是△ABC是底边BC边上的高AD的长,因变量是△ABC的面积;
(2)如果AD为x(cm),面积为y (),可表示为;
(3)当AD=BC时,△ABC的面积为.
( http: / / www.21cnjy.com )
19.(1)阴影部分的面积为:y=32-4x(0<x≤4);(2)PB=3
【解析】试题分析:(1)根据梯形的面积公式得出y与x的函数关系式即可;
(2)利用(1)中所求得出y=20,求出x即可得出答案.21教育网
试题解析:(1)设PB=x,长方形ABCD中,AB=4,BC=8,
则图中阴影部分的面积为:y=(4-x+4)×8=32-4x(0≤x≤4).
(2)当y=20时,20=32-4x,解得x=3,即PB=3.2-1-c-n-j-y
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
