4.1 函数和它的表示法(2)同步练习
文档属性
| 名称 | 4.1 函数和它的表示法(2)同步练习 |

|
|
| 格式 | doc | ||
| 文件大小 | 585.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-02 00:00:00 | ||
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
4.1 函数和它的表示法(2)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.函数的三种表示方法是图象法 、列表法、公式法.
2.用图象法表示函数关系,可以直观地看出因变量如何随自变量变化而变化.
3.用列表法表示函数关系,可以很清楚地看出自变量取的值与因变量的对应值.
4.用公式法表示函数关系,可以方便地计算函数值.
5.函数图象是典型的数形结合,图象应用 ( http: / / www.21cnjy.com )信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.
用图象解决问题时,要理清图象的含义即会识图.
基础知识和能力拓展精练
一、选择题
1.远通工程队承建一条长30km的乡村公路,预计工期为120天,若每天修建公路的长度保持不变,则还未完成的公路长度与施工时间天之间的关系式为( )
A. B. C. D.
2.弹簧挂上物体后会伸长,测得一根弹簧的长度y(cm)与所挂物体的质量x(kg)间有下面的关系:
( http: / / www.21cnjy.com )
下列说法中,不正确的是( )
A. x是自变量,y是x的函数
B. 弹簧不挂重物时长度为0 cm
C. 物体质量每增加1 kg,弹簧长度y增加0.5 cm
D. 所挂物体质量为7 kg时,弹簧长度为13.5 cm
3.一家校办工厂2013年的年产值是15万元,计划从2014年开始,每年增加2万元,则年产值(从2013年开始)(万元)与年数的函数关系式是( )21·世纪*教育网
A. (的整数) B. (的整数)
C. (的整数) D. (的整数)
4.观察表格,则变量y与x的关系式为( )
x 1 2 3 4 …
y 3 4 5 6 …
A. y=3x B. y=x+2 C. y=x﹣2 D. y=x+1
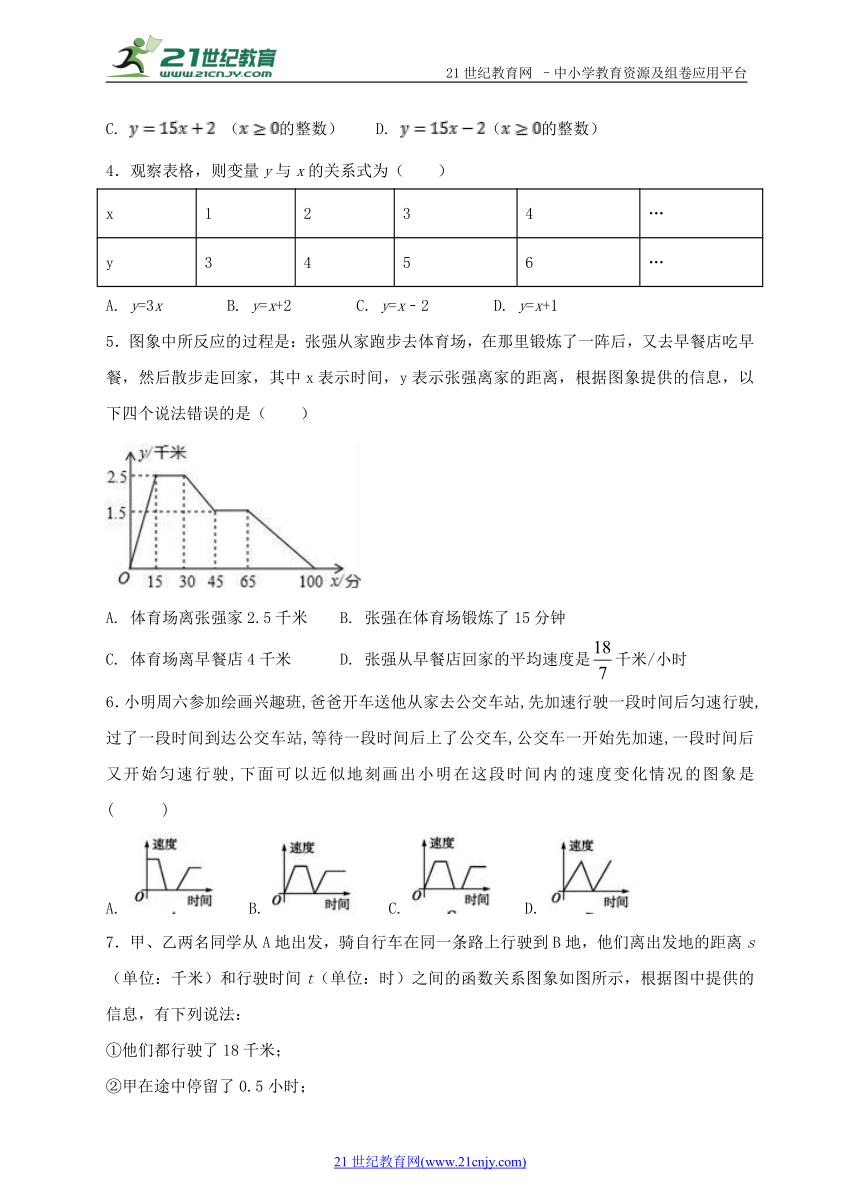
5.图象中所反应的过程是:张强从家跑步去体 ( http: / / www.21cnjy.com )育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法错误的是( )21教育网
( http: / / www.21cnjy.com )
A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是千米/小时
6.小明周六参加绘画兴趣班,爸爸开车送他从 ( http: / / www.21cnjy.com )家去公交车站,先加速行驶一段时间后匀速行驶,过了一段时间到达公交车站,等待一段时间后上了公交车,公交车一开始先加速,一段时间后又开始匀速行驶,下面可以近似地刻画出小明在这段时间内的速度变化情况的图象是( )21教育名师原创作品
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
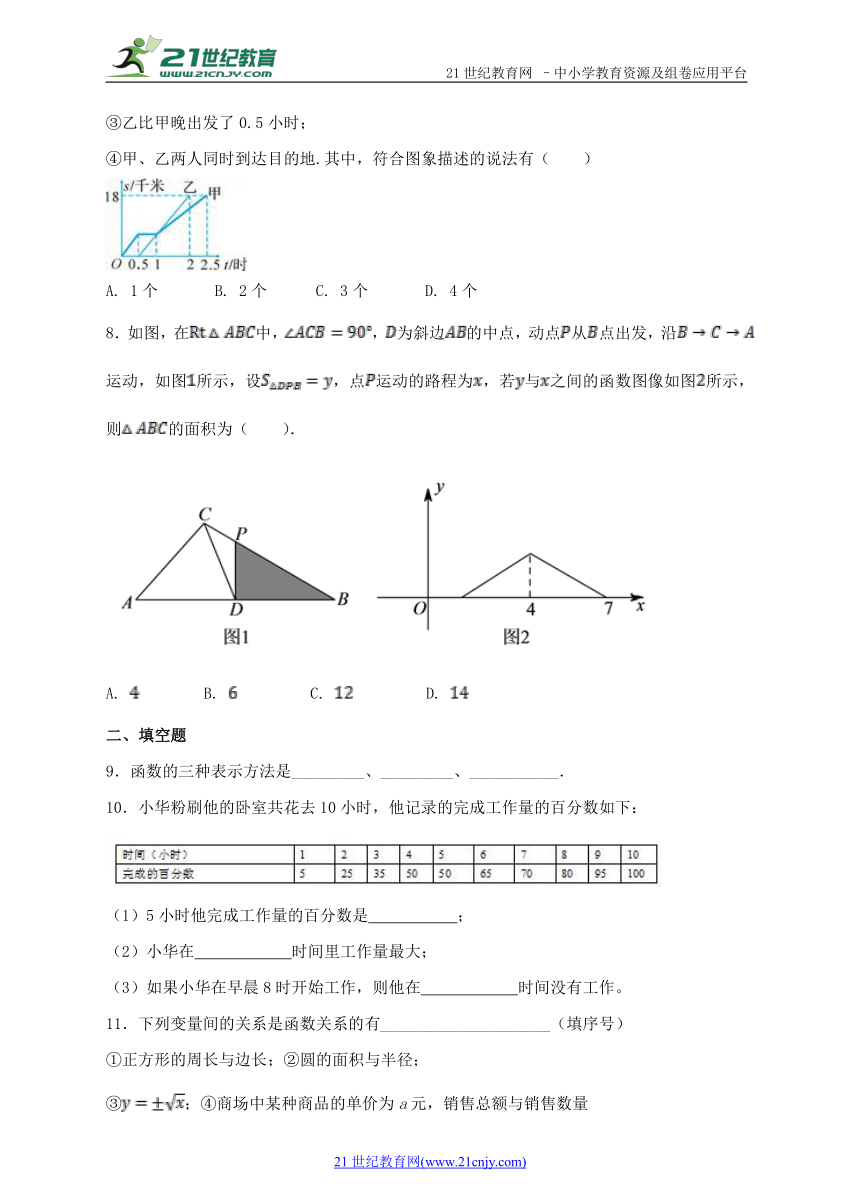
7.甲、乙两名同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(单位:千米)和行驶时间t(单位:时)之间的函数关系图象如图所示,根据图中提供的信息,有下列说法:
①他们都行驶了18千米;
②甲在途中停留了0.5小时;
③乙比甲晚出发了0.5小时;
④甲、乙两人同时到达目的地.其中,符合图象描述的说法有( )
( http: / / www.21cnjy.com )
A. 1个 B. 2个 C. 3个 D. 4个
8.如图,在中,,为斜边的中点,动点从点出发,沿运动,如图所示,设,点运动的路程为,若与之间的函数图像如图所示,则的面积为( ).
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
A. B. C. D.
二、填空题
9.函数的三种表示方法是_________、_________、___________.
10.小华粉刷他的卧室共花去10小时,他记录的完成工作量的百分数如下:
( http: / / www.21cnjy.com )
(1)5小时他完成工作量的百分数是 ;
(2)小华在 时间里工作量最大;
(3)如果小华在早晨8时开始工作,则他在 时间没有工作。
11.下列变量间的关系是函数关系的有_____________________(填序号)
①正方形的周长与边长;②圆的面积与半径;
③;④商场中某种商品的单价为a元,销售总额与销售数量
12.如图所示的函数图象反 ( http: / / www.21cnjy.com )映的过程是:小红从家去书店,又去学校取封信后马上回家,其中x表示时间,y表示小红离她家的距离,则小红从学校回家的平均速度为_______________千米/小时.
( http: / / www.21cnjy.com )
13.某龙舟队参加“国际龙舟节”100 ( http: / / www.21cnjy.com )0 米比赛项目时,路程 y(米)与时间 x(分钟)之间的图象如图所示.根据图中提供的信息,该龙舟队的比赛成绩_____ 分钟.
( http: / / www.21cnjy.com )
14.如图,长方形ABCD中,AB ( http: / / www.21cnjy.com )=5,AD=3,点P从点A出发,沿长方形ABCD的边逆时针运动,设点P运动的距离为x;△APC的面积为y,如果5<x<8,那么y关于x的函数关系式为_____.
( http: / / www.21cnjy.com )
三、解答题
15.下表是某公共电话亭打长途电话的几次收费记录:
时间(分) 1 2 3 4 5 6 7
电话费(元) 0.6 1.2 1.8 2.4 3.0 3.6 4.2
(1) 上表反映了哪两个变量间的关系 哪个是自变量 哪个是因变量
(2) 如果用 x 表示时间,y 表示电话费,那么随 x 的变化,y 的变化趋势是什么
(3) 丽丽打了 5 分钟电话,那么电话费需付多少元
(4) 你能写出 y 与 x 之间的关系式吗
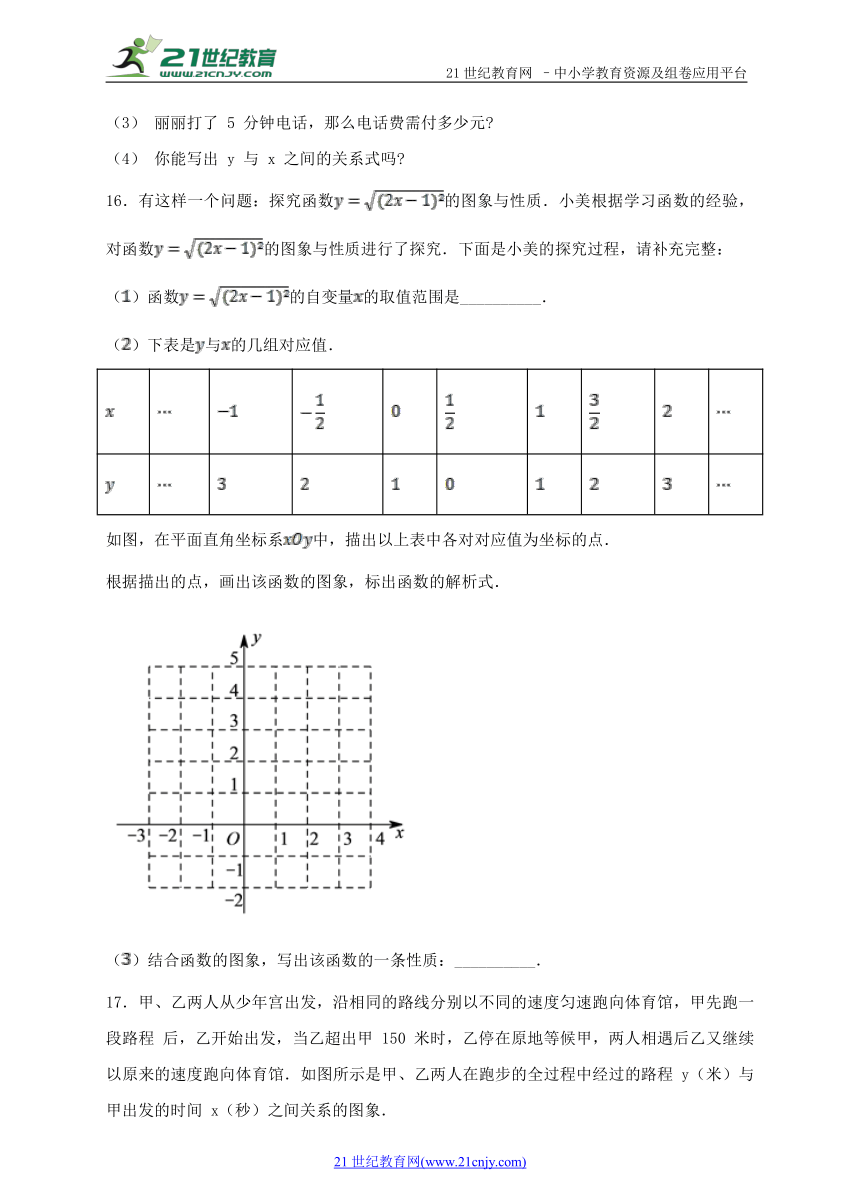
16.有这样一个问题:探究函数的图象与性质.小美根据学习函数的经验,对函数的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
()函数的自变量的取值范围是__________.
()下表是与的几组对应值.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
如图,在平面直角坐标系中,描出以上表中各对对应值为坐标的点.
根据描出的点,画出该函数的图象,标出函数的解析式.
( http: / / www.21cnjy.com )
()结合函数的图象,写出该函数的一条性质:__________.
17.甲、乙两人从少年宫出发,沿相 ( http: / / www.21cnjy.com )同的路线分别以不同的速度匀速跑向体育馆,甲先跑一段路程 后,乙开始出发,当乙超出甲 150 米时,乙停在原地等候甲,两人相遇后乙又继续以原来的速度跑向体育馆.如图所示是甲、乙两人在跑步的全过程中经过的路程 y(米)与甲出发的时间 x(秒)之间关系的图象.21世纪教育网版权所有
( http: / / www.21cnjy.com )
(1) 在跑步的全过程中,甲一共跑了 米,甲的速度为 米/秒.
(2) 求图中标注的 a 的值及乙跑步的速度.
(3) 乙在途中等候了多少时间
18.如图,正方形ABCD的边长为4,动点E ( http: / / www.21cnjy.com )从点A出发,以每秒2个单位的速度沿A→D→A运动,动点G从点A出发,以每秒1个单位的速度沿A→B运动,当有一个点到达终点时,另一点随之也停止运动.过点G作FG⊥AB交AC于点F.设运动时间为t(单位:秒).以FG为一直角边向右作等腰直角三角形FGH,△FGH与正方形ABCD重叠部分的面积为S.
(1)当t=1.5时,S=________;当t=3时,S=________.
(2)设DE=y1,AG=y2,在如图所示的网格坐标系中,画出y1与y2关于t的函数图象.并求当t为何值时,四边形DEGF是平行四边形?21cnjy.com
( http: / / www.21cnjy.com )
参考答案
1.A
【解析】由未完成的公路长度=30-已经完成的公路长度可得:
,即.
故选A.
2.B
【解析】A. 由表中数据知,x是自变量,y是x的函数,正确;
B. ∵由表中数据知,弹簧不挂重物时长度为10 cm,故不正确;
C. 由表中数据知,物体质量每增加1 kg,弹簧长度y增加0.5 cm,正确;
D. 由表中数据知,所挂物体质量为7 kg时,弹簧长度为10+7×0.5=13.5 cm,正确;
故选B.
3.B
【解析】由题意可知,从20 ( http: / / www.21cnjy.com )14年开始,每年在2013年的基础上产值增加2万元,2013年的产值基数是15万元,故之后的每一年都是在前一年的基础上增加2万元,
所以(的整数),
故选B.
【点睛】本题考查了列函数解析式,解题的关键是审清题意,明白增长基数是哪一个,增长幅度是多少.
4.B
【解析】观察图表可知,每对x,y的对应值,y比x大2,
故变量y与x之间的函数关系式:y=x+2.
故选:B.
点睛:本题主要考查了根据条件写出函数关系式.认真审题是解题的关键.
5.C
【解析】试题解析:A、由纵坐标看出,体育场离张强家2.5千米,故A正确;
B、由横坐标看出,30-15=15分钟,张强在体育场锻炼了15分钟,故B正确;
C、由纵坐标看出,2.5-1.5=1千米,体育场离早餐店1千米,故C错误;
D、由纵坐标看出早餐店离家1.5千米,由横坐标看出从早餐店回家用了100-65=35分钟=小时,1.5÷千米/小时,故D正确.【来源:21·世纪·教育·网】
故选C.
【点睛】本题图中折线反映 ( http: / / www.21cnjy.com )的是张强离家的距离y与时间x之间的关系,根据横轴和纵轴上的数据不难解答有关问题.需注意理解时间增多,路程没有变化的函数图象是与x轴平行的一段线段.平均速度=总路程÷总时间.21*cnjy*com
6.C
【解析】试题分析:先加速行驶,可得速度 ( http: / / www.21cnjy.com )变快,图象从原点开始,成上升趋势;再匀速行驶,可得速度不变,图象平行于x轴;到达公交车站,汽车减速,速度变慢,直至变为0,图象成下降趋势;根据等车,可得速度为零;根据公交加速,可得速度变快,图象成上升趋势;根据匀速行驶,可得速度不变,图象平行于x轴.由此可知只有选项C符合题意.
故选C.
点睛:本题考查了函数图象,正确理解函数图象横纵坐标表示的意义,理解问题的过程,能够通过图象得到函数值随自变量的增大是增大还是减小.【出处:21教育名师】
7.C
【解析】解:根据题意和图象可知:①他们都行驶了18千米.②甲车停留了0.5小时.③乙比甲晚出发了0.5小时.故只有④不正确.故选C.【版权所有:21教育】
8.B
【解析】∵是斜边的中点,
∴根据函数的图像可知:,,
∵,
∴,,
故答案为:.
9. 图象法 列表法 解析式法
【解析】函数有三种表示方法——图象法、列表法、解析式法,
故答案为:图象法、列表法、解析式法.
【点睛】本题考查了函数的表达方式,是概念性问题,熟知课本中的概念是解题的关键.
10.50%;第二小时;12~13小时.
【解析】(1)观察表格可得:5小时他完 ( http: / / www.21cnjy.com )成工作量的百分数是50%;(2)由图表可知,在第二小时完成的总工作量的20%,所以在第二小时时间里工作量最大;(3)观察表格可知:开始工作4~5小时工作量都是50%没有发生变化,由小华从早晨8时开始工作,可得小华在12~13小时时间没有工作.21*cnjy*com
点睛:本题考查了函数的表示方法——表格法,比较简单,阅读图表数据,准确获取信息是解题的关键.
11.①②④.
【解析】在一个变化过程中,有两个变 ( http: / / www.21cnjy.com )量x和y,对于x的每一个确定值,y都有唯一的值与之对应,则称y是x的函数,在③中,当x取一个值时,对应的y值有两个,故不是函数,
故答案为:①②④.
12.6.
【解析】小红家与学校的距离为6km,从图象可知她从学校到家用时为3-2=1小时,故从学校到家的平均速度等于6÷1=6 km/h,2-1-c-n-j-y
故答案为:6.
【点睛】本题考查了函数的图象,分段函数,解此题的关键是找到相应的路程与时间,根据速度=路程÷时间得到相应的速度.www.21-cn-jy.com
13.4.8
【解析】由图中的信息可知,该龙舟队前4分钟航行了800米,从第4分钟开始,速度为:(925-800)÷0.5=250(米/分),
∴该龙舟队的比赛成绩为:4+(1000-800)÷250=4+0.8=4.8(分钟).
故答案为:4.8.
14.y=﹣x+20
【解析】试题解析:当5<x<8时,点P在线段BC上,PC=8﹣x,
∴y=PC AB=﹣x+20.
故答案为:y=﹣x+20.
15.(1) 反映的是电话费和时间两个变 ( http: / / www.21cnjy.com )量之间的关系,时间是自变量,电话费是因变量.(2) 每增加 1 分钟,电话费增加 0.6 元.(3) 电话费需付 3 元.(4) y = 0.6x.
【解析】试题分析:
(1)观察、分析所给记录可知,上表反映的是“电话费”和“打电话时间”两个变量之间的关系,其中“时间”是自变量,“电话费”是因变量;
(2)由表中的数据可知,电话费y随通话时间x的增大而增大,x每增加1分钟,y增加0.6元;
(3)由表中信息可知,通话5分钟需付电话费3元;
(4)由表中信息可知,y=0.6x.
试题解析:
(1)表中反映的是:“电话费”和“打电话时间”两个变量之间的关系,其中“时间”是自变量,“电话费”是因变量;2·1·c·n·j·y
(2)若用 x 表示时间,y 表示电话费,则由表中信息可知:电话费y随通话时间x的增大而增大,x每增加1分钟,y增加0.6元;
(3)由表中信息可知,当x=5时,y=3,即通话5分钟需付费3元;
(4)由表中信息可得:y=0.6x.
16.()任意实数()见解析()当时,随增大而增大
【解析】试题分析:
(1)由可知可取任意实数;
(2)根据表格中的数据描点、连线画出图形即可;
(3)本题答案不唯一,只要符合图象所反映的实际情况都可以.
试题解析:
()取值范围是全体实数.
()根据表格中所提供的数据,描点、连线,画出该函数的图象如下图所示:
( http: / / www.21cnjy.com )
()由图可得:当时,随增大而增大(答案不唯一).
17.(1) 900;1.5;(2)a 的值为 750 米,乙的跑步速度为 2.5(米 / 秒);(3)100 秒
【解析】试题分析:
(1)由图中信息可知,甲一共跑了900米,用时600秒,由此即可求得甲的速度为1.5米/秒;
(2)由图中的信息可知,第500秒时,甲共跑了a米,由此结合(1)中所得甲的速度即可求得a的值;
(3)由图中信息结合(2)中所得a的 ( http: / / www.21cnjy.com )值,可知乙在60秒内跑了150米,由此可得乙的速度为:2.5米/秒,由此即可计算出乙从出发到休息时所用时间为750÷2.5=300(秒);由图中信息结合(1)中所得甲的速度可知,乙是在甲出发100秒后出发的;这样结合图中信息就可得乙在中途等候的时间为:500-100-300=100(秒).21·cn·jy·com
试题解析:
(1)由图中信息可知,甲一共跑了900米,用时600秒,
∴甲的速度为:900÷600=1.5(米/秒);
(2)由图中信息可得,图中:a=1.5×500=750(米);
(3)由图中信息结合a=750可得:乙的速度为:(900-750)÷(560-500)=2.5(米/秒),
由图中信息可得:乙出发时甲已经跑了:150÷1.5=100(秒),乙从出发到中途等候时共跑了750÷2.5=300(秒),www-2-1-cnjy-com
∴乙在中途等候的时间为:500-100-300=100(秒).
点睛:本题解题的要点是弄清函数图象中以 ( http: / / www.21cnjy.com )下几个点的实际意义:(1)点A表示甲跑完150米时所用的时间,也是乙出发的时间;(2)B表示乙跑完a米,开始休息时的时间;(3)C点表示甲跑完a米,追上乙时所对应的时间为500秒;(4)D表示乙跑完全程900米时,所对应的时间是第560秒;(5)E表示甲跑完全程900米,用时600秒.
18.(1); ;(2)当t=或t=4时,四边形DEGF是平行四边形.
【解析】试题分析:(1)当t= ( http: / / www.21cnjy.com )1.5时,如图①,重叠部分的面积是△FGH的面积,求出即可;当t=3时,如图②,重叠部分的面积是四边形FGBK的面积,也就是△FGH的面积减去△KBH的面积,求出即可;【来源:21cnj*y.co*m】
(2)进行分类讨论,列出方程即可求出t的值.
试题解析:当t=1.5时,如图①,重叠部分的面积是△FGH的面积,所以S=;
当t=3时,如图②,重叠部分的面积是四边形FGBK的面积,也就是△FGH的面积减去△KBH的面积,所以S=×3×3-×2×2=.
(2)由题意可以求得
y1= ;y2=t(0≤t≤4).<
所以y1与y2关于t的函数图象如图③所示.
因为运动过程中,DE∥FG,所以当DE=FG时,四边形DEGF是平行四边形.
∵FG=AG,
∴DE=AG,
∴y1=y2.由图象可知,有两个t值满足条件:
①当0≤t≤2时,由4-2t=t,解得t= ( http: / / www.21cnjy.com );
②当2所以当t= ( http: / / www.21cnjy.com )或t=4时,四边形DEGF是平行四边形.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.1 函数和它的表示法(2)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.函数的三种表示方法是图象法 、列表法、公式法.
2.用图象法表示函数关系,可以直观地看出因变量如何随自变量变化而变化.
3.用列表法表示函数关系,可以很清楚地看出自变量取的值与因变量的对应值.
4.用公式法表示函数关系,可以方便地计算函数值.
5.函数图象是典型的数形结合,图象应用 ( http: / / www.21cnjy.com )信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.
用图象解决问题时,要理清图象的含义即会识图.
基础知识和能力拓展精练
一、选择题
1.远通工程队承建一条长30km的乡村公路,预计工期为120天,若每天修建公路的长度保持不变,则还未完成的公路长度与施工时间天之间的关系式为( )
A. B. C. D.
2.弹簧挂上物体后会伸长,测得一根弹簧的长度y(cm)与所挂物体的质量x(kg)间有下面的关系:
( http: / / www.21cnjy.com )
下列说法中,不正确的是( )
A. x是自变量,y是x的函数
B. 弹簧不挂重物时长度为0 cm
C. 物体质量每增加1 kg,弹簧长度y增加0.5 cm
D. 所挂物体质量为7 kg时,弹簧长度为13.5 cm
3.一家校办工厂2013年的年产值是15万元,计划从2014年开始,每年增加2万元,则年产值(从2013年开始)(万元)与年数的函数关系式是( )21·世纪*教育网
A. (的整数) B. (的整数)
C. (的整数) D. (的整数)
4.观察表格,则变量y与x的关系式为( )
x 1 2 3 4 …
y 3 4 5 6 …
A. y=3x B. y=x+2 C. y=x﹣2 D. y=x+1
5.图象中所反应的过程是:张强从家跑步去体 ( http: / / www.21cnjy.com )育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法错误的是( )21教育网
( http: / / www.21cnjy.com )
A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是千米/小时
6.小明周六参加绘画兴趣班,爸爸开车送他从 ( http: / / www.21cnjy.com )家去公交车站,先加速行驶一段时间后匀速行驶,过了一段时间到达公交车站,等待一段时间后上了公交车,公交车一开始先加速,一段时间后又开始匀速行驶,下面可以近似地刻画出小明在这段时间内的速度变化情况的图象是( )21教育名师原创作品
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
7.甲、乙两名同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(单位:千米)和行驶时间t(单位:时)之间的函数关系图象如图所示,根据图中提供的信息,有下列说法:
①他们都行驶了18千米;
②甲在途中停留了0.5小时;
③乙比甲晚出发了0.5小时;
④甲、乙两人同时到达目的地.其中,符合图象描述的说法有( )
( http: / / www.21cnjy.com )
A. 1个 B. 2个 C. 3个 D. 4个
8.如图,在中,,为斜边的中点,动点从点出发,沿运动,如图所示,设,点运动的路程为,若与之间的函数图像如图所示,则的面积为( ).
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
A. B. C. D.
二、填空题
9.函数的三种表示方法是_________、_________、___________.
10.小华粉刷他的卧室共花去10小时,他记录的完成工作量的百分数如下:
( http: / / www.21cnjy.com )
(1)5小时他完成工作量的百分数是 ;
(2)小华在 时间里工作量最大;
(3)如果小华在早晨8时开始工作,则他在 时间没有工作。
11.下列变量间的关系是函数关系的有_____________________(填序号)
①正方形的周长与边长;②圆的面积与半径;
③;④商场中某种商品的单价为a元,销售总额与销售数量
12.如图所示的函数图象反 ( http: / / www.21cnjy.com )映的过程是:小红从家去书店,又去学校取封信后马上回家,其中x表示时间,y表示小红离她家的距离,则小红从学校回家的平均速度为_______________千米/小时.
( http: / / www.21cnjy.com )
13.某龙舟队参加“国际龙舟节”100 ( http: / / www.21cnjy.com )0 米比赛项目时,路程 y(米)与时间 x(分钟)之间的图象如图所示.根据图中提供的信息,该龙舟队的比赛成绩_____ 分钟.
( http: / / www.21cnjy.com )
14.如图,长方形ABCD中,AB ( http: / / www.21cnjy.com )=5,AD=3,点P从点A出发,沿长方形ABCD的边逆时针运动,设点P运动的距离为x;△APC的面积为y,如果5<x<8,那么y关于x的函数关系式为_____.
( http: / / www.21cnjy.com )
三、解答题
15.下表是某公共电话亭打长途电话的几次收费记录:
时间(分) 1 2 3 4 5 6 7
电话费(元) 0.6 1.2 1.8 2.4 3.0 3.6 4.2
(1) 上表反映了哪两个变量间的关系 哪个是自变量 哪个是因变量
(2) 如果用 x 表示时间,y 表示电话费,那么随 x 的变化,y 的变化趋势是什么
(3) 丽丽打了 5 分钟电话,那么电话费需付多少元
(4) 你能写出 y 与 x 之间的关系式吗
16.有这样一个问题:探究函数的图象与性质.小美根据学习函数的经验,对函数的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
()函数的自变量的取值范围是__________.
()下表是与的几组对应值.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
如图,在平面直角坐标系中,描出以上表中各对对应值为坐标的点.
根据描出的点,画出该函数的图象,标出函数的解析式.
( http: / / www.21cnjy.com )
()结合函数的图象,写出该函数的一条性质:__________.
17.甲、乙两人从少年宫出发,沿相 ( http: / / www.21cnjy.com )同的路线分别以不同的速度匀速跑向体育馆,甲先跑一段路程 后,乙开始出发,当乙超出甲 150 米时,乙停在原地等候甲,两人相遇后乙又继续以原来的速度跑向体育馆.如图所示是甲、乙两人在跑步的全过程中经过的路程 y(米)与甲出发的时间 x(秒)之间关系的图象.21世纪教育网版权所有
( http: / / www.21cnjy.com )
(1) 在跑步的全过程中,甲一共跑了 米,甲的速度为 米/秒.
(2) 求图中标注的 a 的值及乙跑步的速度.
(3) 乙在途中等候了多少时间
18.如图,正方形ABCD的边长为4,动点E ( http: / / www.21cnjy.com )从点A出发,以每秒2个单位的速度沿A→D→A运动,动点G从点A出发,以每秒1个单位的速度沿A→B运动,当有一个点到达终点时,另一点随之也停止运动.过点G作FG⊥AB交AC于点F.设运动时间为t(单位:秒).以FG为一直角边向右作等腰直角三角形FGH,△FGH与正方形ABCD重叠部分的面积为S.
(1)当t=1.5时,S=________;当t=3时,S=________.
(2)设DE=y1,AG=y2,在如图所示的网格坐标系中,画出y1与y2关于t的函数图象.并求当t为何值时,四边形DEGF是平行四边形?21cnjy.com
( http: / / www.21cnjy.com )
参考答案
1.A
【解析】由未完成的公路长度=30-已经完成的公路长度可得:
,即.
故选A.
2.B
【解析】A. 由表中数据知,x是自变量,y是x的函数,正确;
B. ∵由表中数据知,弹簧不挂重物时长度为10 cm,故不正确;
C. 由表中数据知,物体质量每增加1 kg,弹簧长度y增加0.5 cm,正确;
D. 由表中数据知,所挂物体质量为7 kg时,弹簧长度为10+7×0.5=13.5 cm,正确;
故选B.
3.B
【解析】由题意可知,从20 ( http: / / www.21cnjy.com )14年开始,每年在2013年的基础上产值增加2万元,2013年的产值基数是15万元,故之后的每一年都是在前一年的基础上增加2万元,
所以(的整数),
故选B.
【点睛】本题考查了列函数解析式,解题的关键是审清题意,明白增长基数是哪一个,增长幅度是多少.
4.B
【解析】观察图表可知,每对x,y的对应值,y比x大2,
故变量y与x之间的函数关系式:y=x+2.
故选:B.
点睛:本题主要考查了根据条件写出函数关系式.认真审题是解题的关键.
5.C
【解析】试题解析:A、由纵坐标看出,体育场离张强家2.5千米,故A正确;
B、由横坐标看出,30-15=15分钟,张强在体育场锻炼了15分钟,故B正确;
C、由纵坐标看出,2.5-1.5=1千米,体育场离早餐店1千米,故C错误;
D、由纵坐标看出早餐店离家1.5千米,由横坐标看出从早餐店回家用了100-65=35分钟=小时,1.5÷千米/小时,故D正确.【来源:21·世纪·教育·网】
故选C.
【点睛】本题图中折线反映 ( http: / / www.21cnjy.com )的是张强离家的距离y与时间x之间的关系,根据横轴和纵轴上的数据不难解答有关问题.需注意理解时间增多,路程没有变化的函数图象是与x轴平行的一段线段.平均速度=总路程÷总时间.21*cnjy*com
6.C
【解析】试题分析:先加速行驶,可得速度 ( http: / / www.21cnjy.com )变快,图象从原点开始,成上升趋势;再匀速行驶,可得速度不变,图象平行于x轴;到达公交车站,汽车减速,速度变慢,直至变为0,图象成下降趋势;根据等车,可得速度为零;根据公交加速,可得速度变快,图象成上升趋势;根据匀速行驶,可得速度不变,图象平行于x轴.由此可知只有选项C符合题意.
故选C.
点睛:本题考查了函数图象,正确理解函数图象横纵坐标表示的意义,理解问题的过程,能够通过图象得到函数值随自变量的增大是增大还是减小.【出处:21教育名师】
7.C
【解析】解:根据题意和图象可知:①他们都行驶了18千米.②甲车停留了0.5小时.③乙比甲晚出发了0.5小时.故只有④不正确.故选C.【版权所有:21教育】
8.B
【解析】∵是斜边的中点,
∴根据函数的图像可知:,,
∵,
∴,,
故答案为:.
9. 图象法 列表法 解析式法
【解析】函数有三种表示方法——图象法、列表法、解析式法,
故答案为:图象法、列表法、解析式法.
【点睛】本题考查了函数的表达方式,是概念性问题,熟知课本中的概念是解题的关键.
10.50%;第二小时;12~13小时.
【解析】(1)观察表格可得:5小时他完 ( http: / / www.21cnjy.com )成工作量的百分数是50%;(2)由图表可知,在第二小时完成的总工作量的20%,所以在第二小时时间里工作量最大;(3)观察表格可知:开始工作4~5小时工作量都是50%没有发生变化,由小华从早晨8时开始工作,可得小华在12~13小时时间没有工作.21*cnjy*com
点睛:本题考查了函数的表示方法——表格法,比较简单,阅读图表数据,准确获取信息是解题的关键.
11.①②④.
【解析】在一个变化过程中,有两个变 ( http: / / www.21cnjy.com )量x和y,对于x的每一个确定值,y都有唯一的值与之对应,则称y是x的函数,在③中,当x取一个值时,对应的y值有两个,故不是函数,
故答案为:①②④.
12.6.
【解析】小红家与学校的距离为6km,从图象可知她从学校到家用时为3-2=1小时,故从学校到家的平均速度等于6÷1=6 km/h,2-1-c-n-j-y
故答案为:6.
【点睛】本题考查了函数的图象,分段函数,解此题的关键是找到相应的路程与时间,根据速度=路程÷时间得到相应的速度.www.21-cn-jy.com
13.4.8
【解析】由图中的信息可知,该龙舟队前4分钟航行了800米,从第4分钟开始,速度为:(925-800)÷0.5=250(米/分),
∴该龙舟队的比赛成绩为:4+(1000-800)÷250=4+0.8=4.8(分钟).
故答案为:4.8.
14.y=﹣x+20
【解析】试题解析:当5<x<8时,点P在线段BC上,PC=8﹣x,
∴y=PC AB=﹣x+20.
故答案为:y=﹣x+20.
15.(1) 反映的是电话费和时间两个变 ( http: / / www.21cnjy.com )量之间的关系,时间是自变量,电话费是因变量.(2) 每增加 1 分钟,电话费增加 0.6 元.(3) 电话费需付 3 元.(4) y = 0.6x.
【解析】试题分析:
(1)观察、分析所给记录可知,上表反映的是“电话费”和“打电话时间”两个变量之间的关系,其中“时间”是自变量,“电话费”是因变量;
(2)由表中的数据可知,电话费y随通话时间x的增大而增大,x每增加1分钟,y增加0.6元;
(3)由表中信息可知,通话5分钟需付电话费3元;
(4)由表中信息可知,y=0.6x.
试题解析:
(1)表中反映的是:“电话费”和“打电话时间”两个变量之间的关系,其中“时间”是自变量,“电话费”是因变量;2·1·c·n·j·y
(2)若用 x 表示时间,y 表示电话费,则由表中信息可知:电话费y随通话时间x的增大而增大,x每增加1分钟,y增加0.6元;
(3)由表中信息可知,当x=5时,y=3,即通话5分钟需付费3元;
(4)由表中信息可得:y=0.6x.
16.()任意实数()见解析()当时,随增大而增大
【解析】试题分析:
(1)由可知可取任意实数;
(2)根据表格中的数据描点、连线画出图形即可;
(3)本题答案不唯一,只要符合图象所反映的实际情况都可以.
试题解析:
()取值范围是全体实数.
()根据表格中所提供的数据,描点、连线,画出该函数的图象如下图所示:
( http: / / www.21cnjy.com )
()由图可得:当时,随增大而增大(答案不唯一).
17.(1) 900;1.5;(2)a 的值为 750 米,乙的跑步速度为 2.5(米 / 秒);(3)100 秒
【解析】试题分析:
(1)由图中信息可知,甲一共跑了900米,用时600秒,由此即可求得甲的速度为1.5米/秒;
(2)由图中的信息可知,第500秒时,甲共跑了a米,由此结合(1)中所得甲的速度即可求得a的值;
(3)由图中信息结合(2)中所得a的 ( http: / / www.21cnjy.com )值,可知乙在60秒内跑了150米,由此可得乙的速度为:2.5米/秒,由此即可计算出乙从出发到休息时所用时间为750÷2.5=300(秒);由图中信息结合(1)中所得甲的速度可知,乙是在甲出发100秒后出发的;这样结合图中信息就可得乙在中途等候的时间为:500-100-300=100(秒).21·cn·jy·com
试题解析:
(1)由图中信息可知,甲一共跑了900米,用时600秒,
∴甲的速度为:900÷600=1.5(米/秒);
(2)由图中信息可得,图中:a=1.5×500=750(米);
(3)由图中信息结合a=750可得:乙的速度为:(900-750)÷(560-500)=2.5(米/秒),
由图中信息可得:乙出发时甲已经跑了:150÷1.5=100(秒),乙从出发到中途等候时共跑了750÷2.5=300(秒),www-2-1-cnjy-com
∴乙在中途等候的时间为:500-100-300=100(秒).
点睛:本题解题的要点是弄清函数图象中以 ( http: / / www.21cnjy.com )下几个点的实际意义:(1)点A表示甲跑完150米时所用的时间,也是乙出发的时间;(2)B表示乙跑完a米,开始休息时的时间;(3)C点表示甲跑完a米,追上乙时所对应的时间为500秒;(4)D表示乙跑完全程900米时,所对应的时间是第560秒;(5)E表示甲跑完全程900米,用时600秒.
18.(1); ;(2)当t=或t=4时,四边形DEGF是平行四边形.
【解析】试题分析:(1)当t= ( http: / / www.21cnjy.com )1.5时,如图①,重叠部分的面积是△FGH的面积,求出即可;当t=3时,如图②,重叠部分的面积是四边形FGBK的面积,也就是△FGH的面积减去△KBH的面积,求出即可;【来源:21cnj*y.co*m】
(2)进行分类讨论,列出方程即可求出t的值.
试题解析:当t=1.5时,如图①,重叠部分的面积是△FGH的面积,所以S=;
当t=3时,如图②,重叠部分的面积是四边形FGBK的面积,也就是△FGH的面积减去△KBH的面积,所以S=×3×3-×2×2=.
(2)由题意可以求得
y1= ;y2=t(0≤t≤4).<
所以y1与y2关于t的函数图象如图③所示.
因为运动过程中,DE∥FG,所以当DE=FG时,四边形DEGF是平行四边形.
∵FG=AG,
∴DE=AG,
∴y1=y2.由图象可知,有两个t值满足条件:
①当0≤t≤2时,由4-2t=t,解得t= ( http: / / www.21cnjy.com );
②当2
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
