23.1图形的旋转 课件
图片预览





文档简介
课件25张PPT。23.1 图形的旋转感受旋转水
车 以上情景中的转动现象,有什么共同特征? 钟表的指针在转动过程中,其形状、
大小、位置是否发生改变?
飞机的螺旋桨、电风扇的叶轮的转动呢?观察思考图形的旋转︵
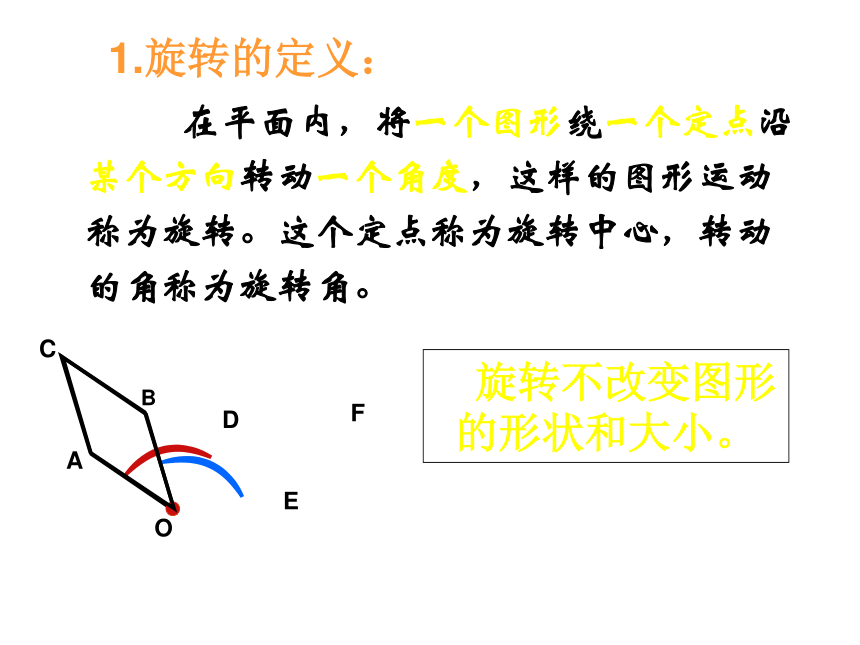
︵FABCDEO 旋转不改变图形的形状和大小。 1.旋转的定义:
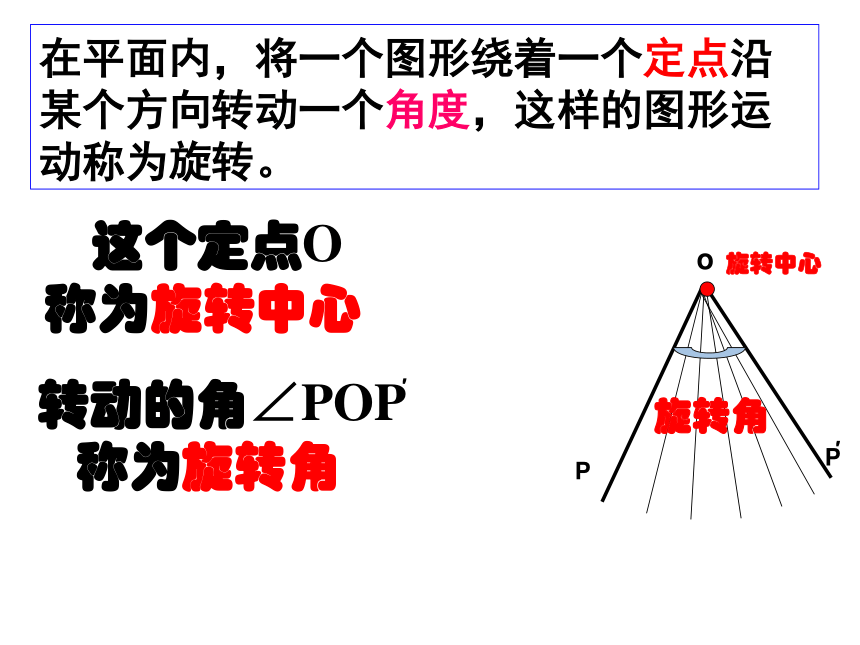
在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。这个定点称为旋转中心,转动的角称为旋转角。 这个定点O
称为旋转中心旋转角旋转中心在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。Po转动的角∠POP
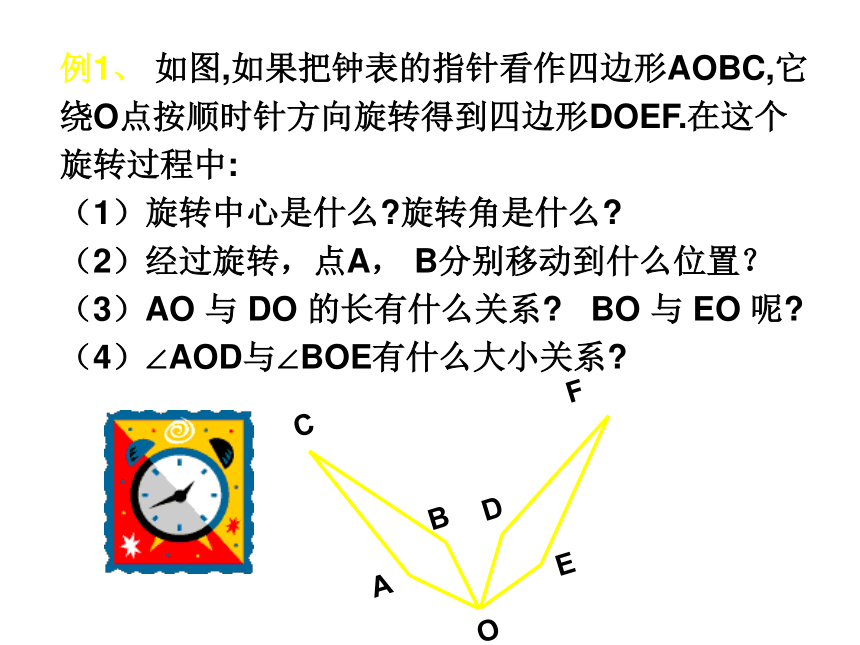
称为旋转角′例1、 如图,如果把钟表的指针看作四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中:
(1)旋转中心是什么?旋转角是什么?
(2)经过旋转,点A, B分别移动到什么位置?
(3)AO 与 DO 的长有什么关系? BO 与 EO 呢?
(4)∠AOD与∠BOE有什么大小关系?
◆旋转前、后的图形 . ◆对应点到旋转中心的距离 . ◆对应点与旋转中心所连线段的夹角等于 . ◆图形的旋转是由 和旋转的______决定. 相等旋转角全等旋转中心角度﹑方向 旋转的基本性质动态演示OP′P 钟表的分针匀速旋转一周需要60分钟.
(1)指出它的旋转中心是( )
(2)经过20分钟,分针旋转了( )度?想一想点O 如图,如果把四边形AOBC绕着O点旋转得到四边形DOEF. 在这个旋转过程中:
⑴旋转中心是( )。
⑵经过旋转,点A和点B分别移动到( )的位置。
⑶旋转角是( )。
⑷AO与DO的长度关系是( )。
⑸∠AOD与∠BOE的
大小关系是( )旋转中心是O点D和点EAO=DO;BO=EO∠AOD=∠BOE∠AOD和∠BOEBACODEF议一议0ABC·A′B′C′90°做一做如图,如果旋转中心在△ABC的外面点O处,逆时针转动90°,将整个△ABC旋转到△ ABC 的位置,那么这两个三角形的顶点、边与角是如何对应的呢?′′′例1、如图,△ABC是等边三角形,D是BC上一点,△ABD经过旋转后到达△ACE的位置。
(1)旋转中心是哪一点? (2)旋转了多少度? (3)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?研讨应用解 (1)旋转中心是点A.(3)点M 转到了AC的中点位置上例3、如图11.2.7(1)点M是线段AB上一点,将线段AB绕着点M顺时针方向旋转90,旋转后的线段与原线段的位置有何关系?,如果逆时针方向旋转90呢?研讨应用例2、如图,正方形ABCD和正方形CDEF有公共边CD,请设计方案,使正方形ABCD旋转后能与正方形CDEF重合,你能写出几种方案?ABCDEF·O解:方案一:把正方形ABCD绕点D顺时针旋转90°.方案二:把正方形ABCD绕点C逆时针旋转90°.方案三:把正方形ABCD绕CD的中点O旋转180°.研讨应用动动脑筋 每组图形中的一个,是怎样旋转变换成另一个的?两个直角三角形两个等腰直角三角形1、旋转的概念2、旋转中心与旋转角3、旋转的性质总结梳理 内化目标CA达标检测 反思目标A454上交作业:
教科书第62页习题23.1第3,4,5题 .
车 以上情景中的转动现象,有什么共同特征? 钟表的指针在转动过程中,其形状、
大小、位置是否发生改变?
飞机的螺旋桨、电风扇的叶轮的转动呢?观察思考图形的旋转︵
︵FABCDEO 旋转不改变图形的形状和大小。 1.旋转的定义:
在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。这个定点称为旋转中心,转动的角称为旋转角。 这个定点O
称为旋转中心旋转角旋转中心在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。Po转动的角∠POP
称为旋转角′例1、 如图,如果把钟表的指针看作四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中:
(1)旋转中心是什么?旋转角是什么?
(2)经过旋转,点A, B分别移动到什么位置?
(3)AO 与 DO 的长有什么关系? BO 与 EO 呢?
(4)∠AOD与∠BOE有什么大小关系?
◆旋转前、后的图形 . ◆对应点到旋转中心的距离 . ◆对应点与旋转中心所连线段的夹角等于 . ◆图形的旋转是由 和旋转的______决定. 相等旋转角全等旋转中心角度﹑方向 旋转的基本性质动态演示OP′P 钟表的分针匀速旋转一周需要60分钟.
(1)指出它的旋转中心是( )
(2)经过20分钟,分针旋转了( )度?想一想点O 如图,如果把四边形AOBC绕着O点旋转得到四边形DOEF. 在这个旋转过程中:
⑴旋转中心是( )。
⑵经过旋转,点A和点B分别移动到( )的位置。
⑶旋转角是( )。
⑷AO与DO的长度关系是( )。
⑸∠AOD与∠BOE的
大小关系是( )旋转中心是O点D和点EAO=DO;BO=EO∠AOD=∠BOE∠AOD和∠BOEBACODEF议一议0ABC·A′B′C′90°做一做如图,如果旋转中心在△ABC的外面点O处,逆时针转动90°,将整个△ABC旋转到△ ABC 的位置,那么这两个三角形的顶点、边与角是如何对应的呢?′′′例1、如图,△ABC是等边三角形,D是BC上一点,△ABD经过旋转后到达△ACE的位置。
(1)旋转中心是哪一点? (2)旋转了多少度? (3)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?研讨应用解 (1)旋转中心是点A.(3)点M 转到了AC的中点位置上例3、如图11.2.7(1)点M是线段AB上一点,将线段AB绕着点M顺时针方向旋转90,旋转后的线段与原线段的位置有何关系?,如果逆时针方向旋转90呢?研讨应用例2、如图,正方形ABCD和正方形CDEF有公共边CD,请设计方案,使正方形ABCD旋转后能与正方形CDEF重合,你能写出几种方案?ABCDEF·O解:方案一:把正方形ABCD绕点D顺时针旋转90°.方案二:把正方形ABCD绕点C逆时针旋转90°.方案三:把正方形ABCD绕CD的中点O旋转180°.研讨应用动动脑筋 每组图形中的一个,是怎样旋转变换成另一个的?两个直角三角形两个等腰直角三角形1、旋转的概念2、旋转中心与旋转角3、旋转的性质总结梳理 内化目标CA达标检测 反思目标A454上交作业:
教科书第62页习题23.1第3,4,5题 .
同课章节目录
