26.1.2反比例函数的图象与性质综合运用 课件
文档属性
| 名称 | 26.1.2反比例函数的图象与性质综合运用 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 800.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-02 11:06:03 | ||
图片预览



文档简介
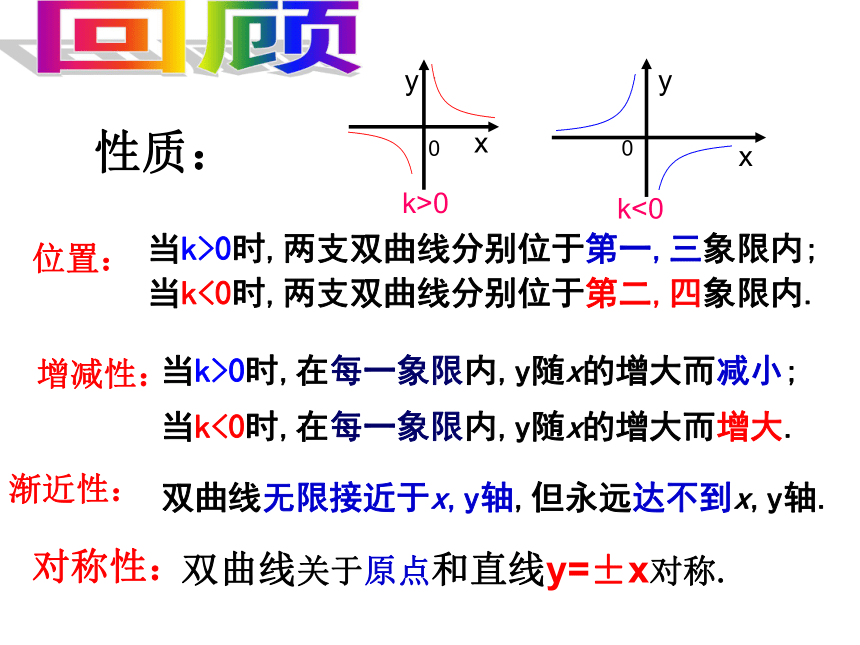
课件32张PPT。26.1.2反比例函数的图像与性质综合运用(2)性质:当k>0时,两支双曲线分别位于第一,三象限内;
当k<0时,两支双曲线分别位于第二,四象限内.双曲线关于原点和直线y=±x对称.双曲线无限接近于x,y轴,但永远达不到x,y轴.当k>0时,在每一象限内,y随x的增大而减小;
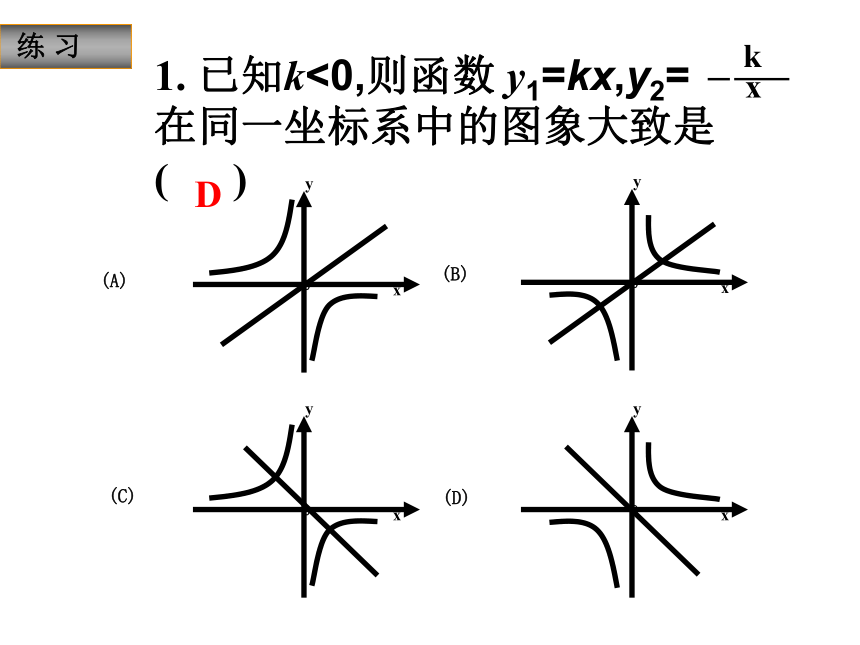
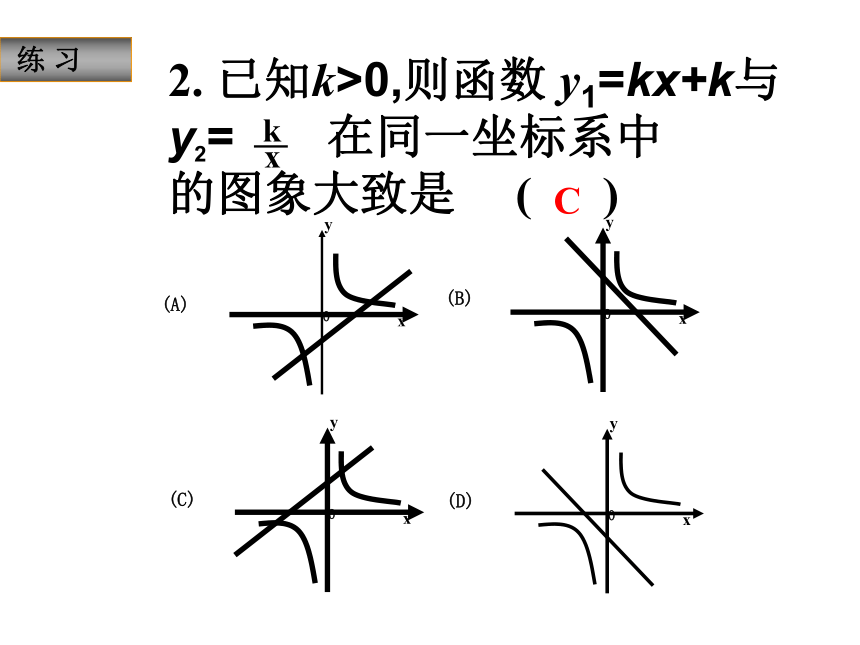
当k<0时,在每一象限内,y随x的增大而增大.位置:增减性:渐近性:对称性:回顾 练 习 1. 已知k<0,则函数 y1=kx,y2= 在同一坐标系中的图象大致是 ( )D 练 习 2. 已知k>0,则函数 y1=kx+k与y2= 在同一坐标系中
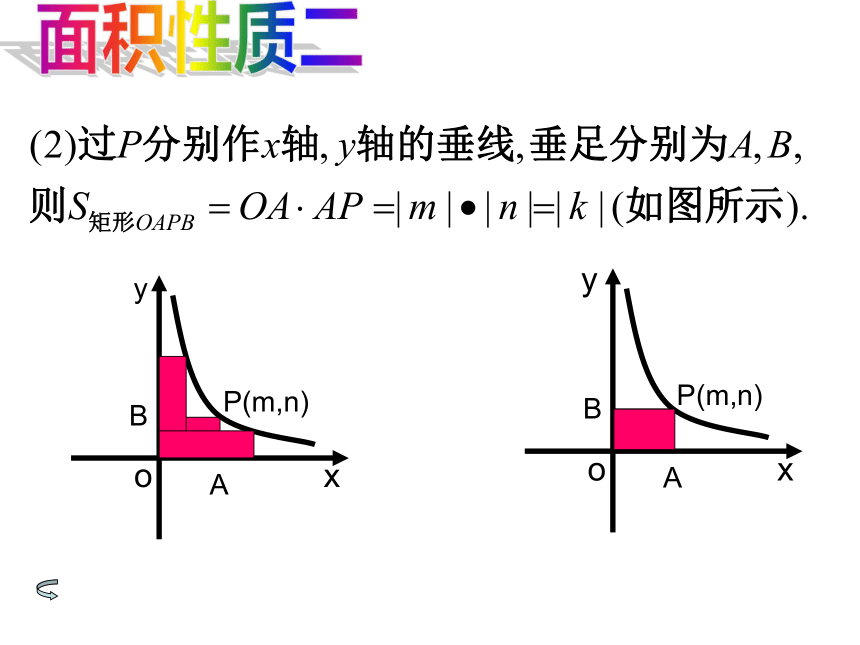
的图象大致是 ( )C如图函数
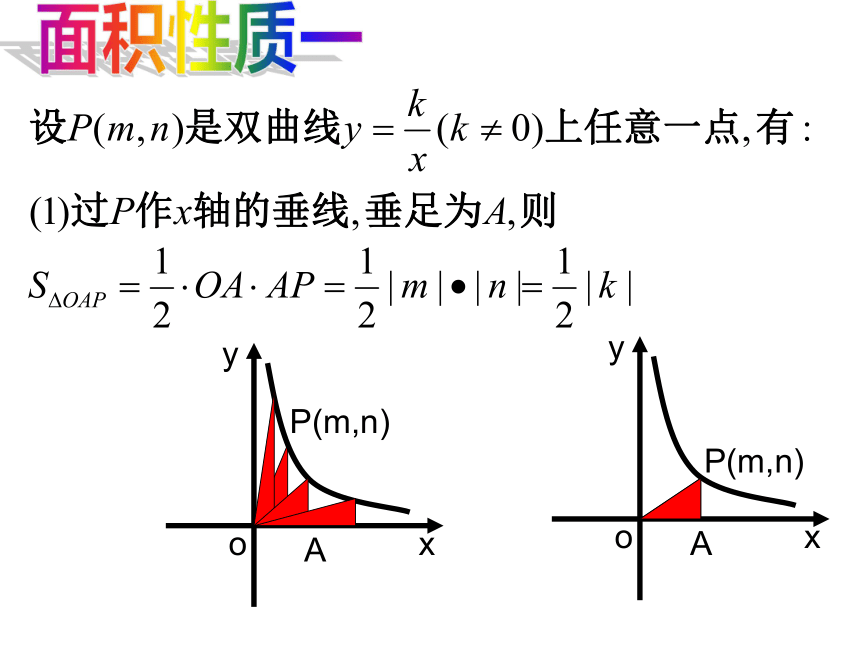
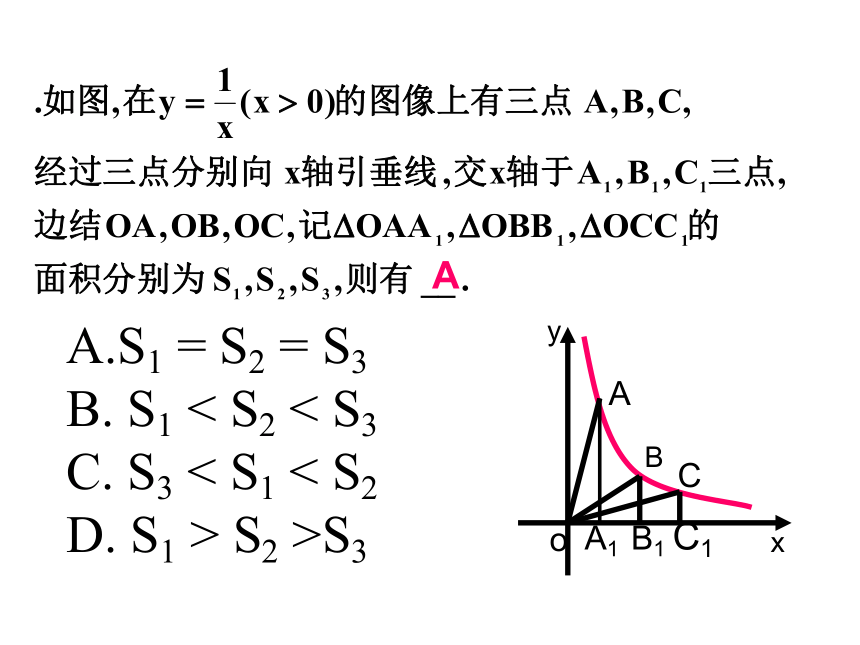
在同一坐标系中的大致图象是( )D面积性质一面积性质二A.S1 = S2 = S3
B. S1 < S2 < S3
C. S3 < S1 < S2
D. S1 > S2 >S3 S2A如图所示,A(x1 ,y1)、B(x2 ,y2)、
C(x3 ,y3)是函数y= 的图象在第一象限分支上的三个点,且 x1< x2 < x3 ,过A、B、C三点分别作坐标轴的垂线,得矩形ADOH、BEON、CFOP,它们的面积分别为S1、S2、S3,则下列结论中正确的是( ) 1A、S1B、S3 C、S2< S3< S1
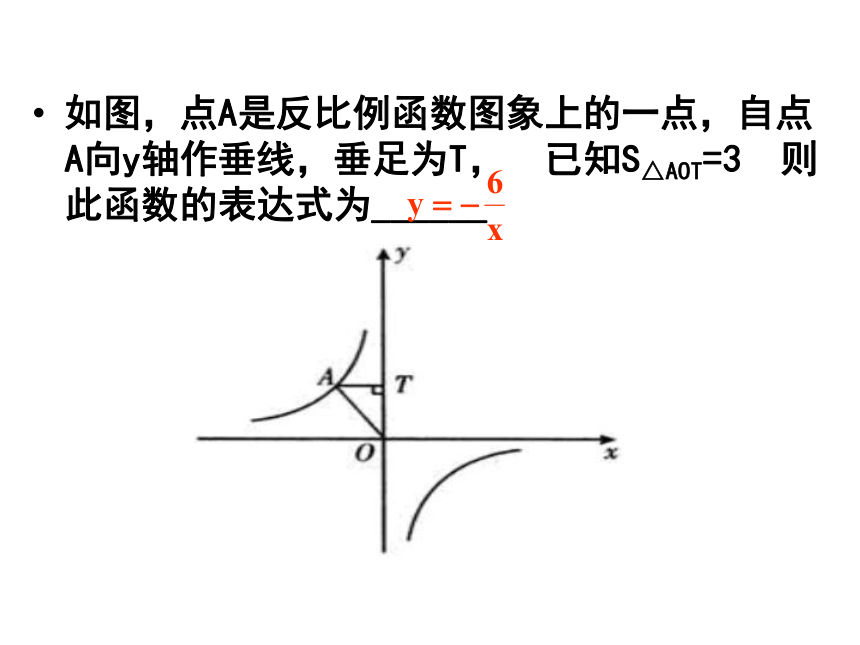
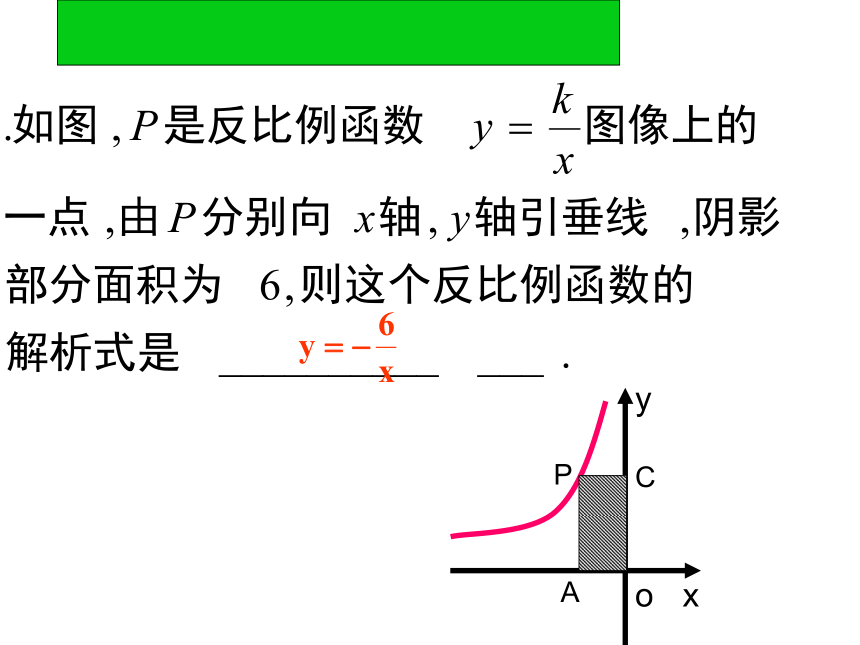
D、S1= S2 = S3D如图,点A是反比例函数图象上的一点,自点A向y轴作垂线,垂足为T,已知S△AOT=3 则此函数的表达式为______面积性质三A.S = 2 B.2C.S = 4 D.S>4解:由上述性质(3)可知,
S△ABC = 2|k| = 4C6C考察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .-1-10如图,已知一次函数y=kx+b(k≠0)的图象与
x轴.y轴分别交于A.B两点,且与反比例函数
y=m/x(m≠0)的图象在第一象限内交于C点,CD
垂直于x轴,垂足为点D,若OA=OB=OD=1.
(1)求点A.B.D的坐标;
(2)求一次函数和
反比例函数的解析式D学以致用解(1)A(-1,0)B(1,0)
C(1,0)(2)把A(-1,1)B(1,0)代入y=kx+b中得 b=1 -k+b=0 ∴k=1 ∴y=x+1
当x=1时,y=1+1=2 ∴C(1,2)
把C(1,2)代入y=m/x中 2=m/1
∴m=2 ∴y=2/x 如图:一次函数y=ax+b的图象与反比例函数
y= 交于M (2,m) 、N (-1,-4)两点
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出反比例函数的值大于一次函数的值的x的取值范围。N(-1,-4)M(2,m)(1)求反比例函数和一次函数的解析式;解(1)∵点N(-1,-4)在反比例函数图象上
∴k=4, ∴y=
又∵点M(2,m)在反比例函数图象上
∴m=2 ∴M(2,2)
∵点M、N都y=ax+b的图象上
∴解得a=2,b= -2
∴y= 2x-2N(-1,-4)M(2,m)(2)观察图象得:
当x<-1或0y2.(2)求出点D的坐标;(1)分别求直线AB与双曲线的解析式;求(1)一次函数的解析式
(2)根据图像写出使一 次函数的值小于反比例函数的值的x的取值范围。超越自我23.(10分)如图,已知正比例函数y=2x和反比例函数的图象交于点 A(m,-2). (1)求反比例函数的解析式; (2)观察图象,直接写出正比例函数值大于反比例函数值时自变量的取值范围; (3)若双曲线上点C(2,n)沿OA方向平移 个单位长度得到点B,判断四边形OABC的形状并证明你的结论. 23.(8分)如图,点B(3,3)在双曲线(x>0)上,点D在双曲线 (x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
(1)求的值;
(2)求点A的坐标. EF……请谈谈你的收获
当k<0时,两支双曲线分别位于第二,四象限内.双曲线关于原点和直线y=±x对称.双曲线无限接近于x,y轴,但永远达不到x,y轴.当k>0时,在每一象限内,y随x的增大而减小;
当k<0时,在每一象限内,y随x的增大而增大.位置:增减性:渐近性:对称性:回顾 练 习 1. 已知k<0,则函数 y1=kx,y2= 在同一坐标系中的图象大致是 ( )D 练 习 2. 已知k>0,则函数 y1=kx+k与y2= 在同一坐标系中
的图象大致是 ( )C如图函数
在同一坐标系中的大致图象是( )D面积性质一面积性质二A.S1 = S2 = S3
B. S1 < S2 < S3
C. S3 < S1 < S2
D. S1 > S2 >S3 S2A如图所示,A(x1 ,y1)、B(x2 ,y2)、
C(x3 ,y3)是函数y= 的图象在第一象限分支上的三个点,且 x1< x2 < x3 ,过A、B、C三点分别作坐标轴的垂线,得矩形ADOH、BEON、CFOP,它们的面积分别为S1、S2、S3,则下列结论中正确的是( ) 1A、S1
D、S1= S2 = S3D如图,点A是反比例函数图象上的一点,自点A向y轴作垂线,垂足为T,已知S△AOT=3 则此函数的表达式为______面积性质三A.S = 2 B.2
S△ABC = 2|k| = 4C6C考察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .-1-1
x轴.y轴分别交于A.B两点,且与反比例函数
y=m/x(m≠0)的图象在第一象限内交于C点,CD
垂直于x轴,垂足为点D,若OA=OB=OD=1.
(1)求点A.B.D的坐标;
(2)求一次函数和
反比例函数的解析式D学以致用解(1)A(-1,0)B(1,0)
C(1,0)(2)把A(-1,1)B(1,0)代入y=kx+b中得 b=1 -k+b=0 ∴k=1 ∴y=x+1
当x=1时,y=1+1=2 ∴C(1,2)
把C(1,2)代入y=m/x中 2=m/1
∴m=2 ∴y=2/x 如图:一次函数y=ax+b的图象与反比例函数
y= 交于M (2,m) 、N (-1,-4)两点
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出反比例函数的值大于一次函数的值的x的取值范围。N(-1,-4)M(2,m)(1)求反比例函数和一次函数的解析式;解(1)∵点N(-1,-4)在反比例函数图象上
∴k=4, ∴y=
又∵点M(2,m)在反比例函数图象上
∴m=2 ∴M(2,2)
∵点M、N都y=ax+b的图象上
∴解得a=2,b= -2
∴y= 2x-2N(-1,-4)M(2,m)(2)观察图象得:
当x<-1或0
(2)根据图像写出使一 次函数的值小于反比例函数的值的x的取值范围。超越自我23.(10分)如图,已知正比例函数y=2x和反比例函数的图象交于点 A(m,-2). (1)求反比例函数的解析式; (2)观察图象,直接写出正比例函数值大于反比例函数值时自变量的取值范围; (3)若双曲线上点C(2,n)沿OA方向平移 个单位长度得到点B,判断四边形OABC的形状并证明你的结论. 23.(8分)如图,点B(3,3)在双曲线(x>0)上,点D在双曲线 (x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
(1)求的值;
(2)求点A的坐标. EF……请谈谈你的收获
