26.1.2反比例函数的图象和性质(1) 课件
文档属性
| 名称 | 26.1.2反比例函数的图象和性质(1) 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 711.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-02 10:57:48 | ||
图片预览




文档简介
课件31张PPT。26.1.2
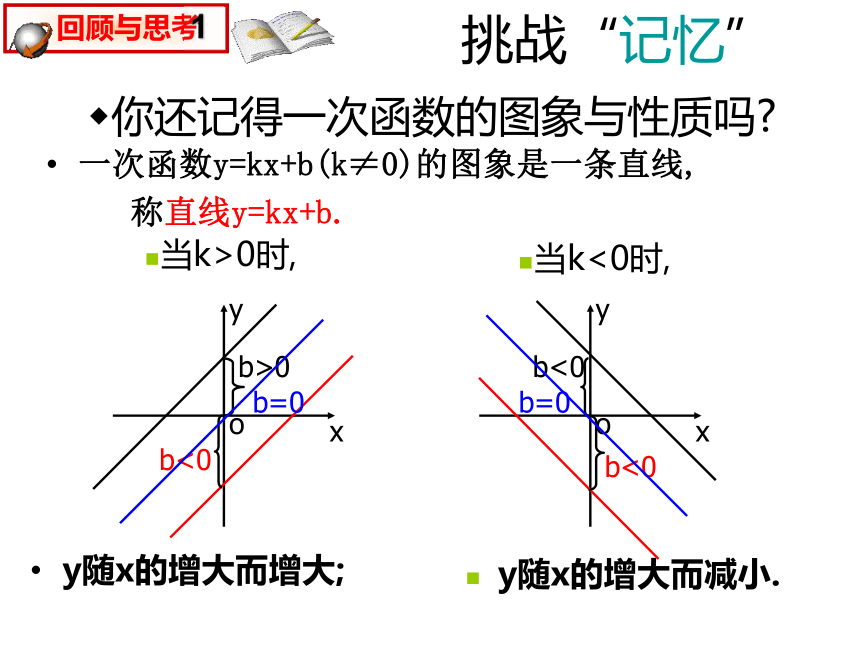
反比例函数的图象和性质(1)(2)你还记得正比例函数y=kx (k≠0)的图像和性质吗?温故导新(1)根据上节课的学习,说说你记忆中的反比例函数.挑战“记忆”你还记得一次函数的图象与性质吗?一次函数y=kx+b(k≠0)的图象是一条直线,
称直线y=kx+b.y随x的增大而增大;y随x的增大而减小.当k>0时,当k<0时,位置增减性位置增减性y=kx ( k≠0 ) 直线一、三象限从左到右上升
y随x的增大而增大二、四象限 从左到右下降
y随x的增大而减小
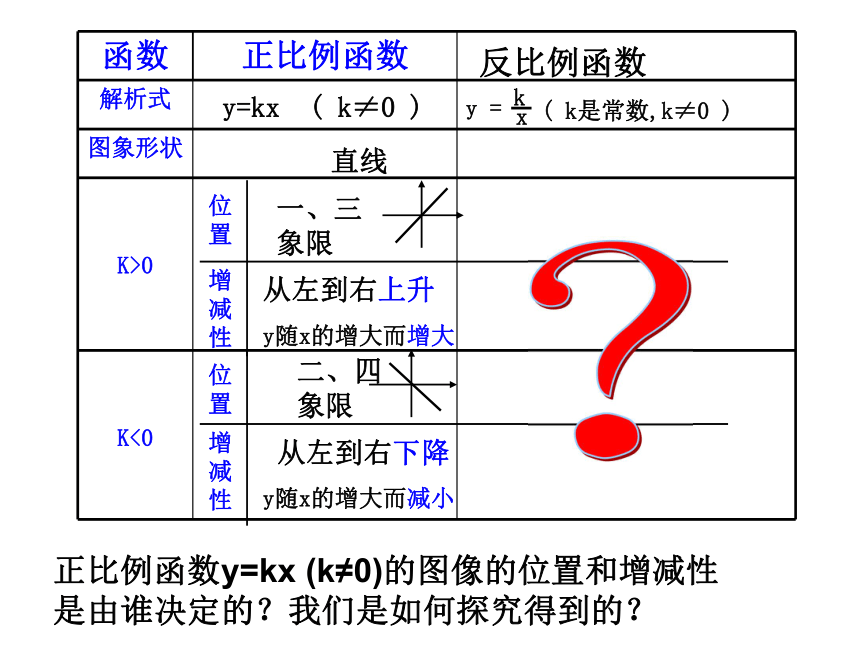
反比例函数?正比例函数y=kx (k≠0)的图像的位置和增减性是由谁决定的?我们是如何探究得到的?
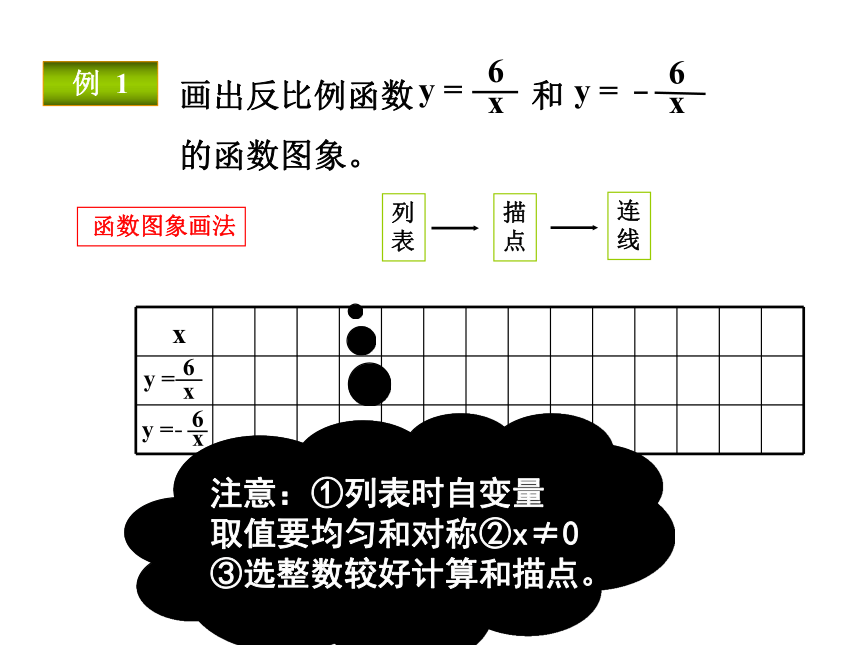
“预见性”,猜一猜反比例函数的图象又会是什么样子呢?你还记得作函数图象的一般步骤吗?用图象法表示函数关系时,首先在自变量的取值范围内取一些值,列表,描点,连线(按自变量从小到大的顺序,用一条平滑的曲线连接起来). 函数图象画法列
表描
点连
线 描点法注意:①列表时自变量
取值要均匀和对称②x≠0
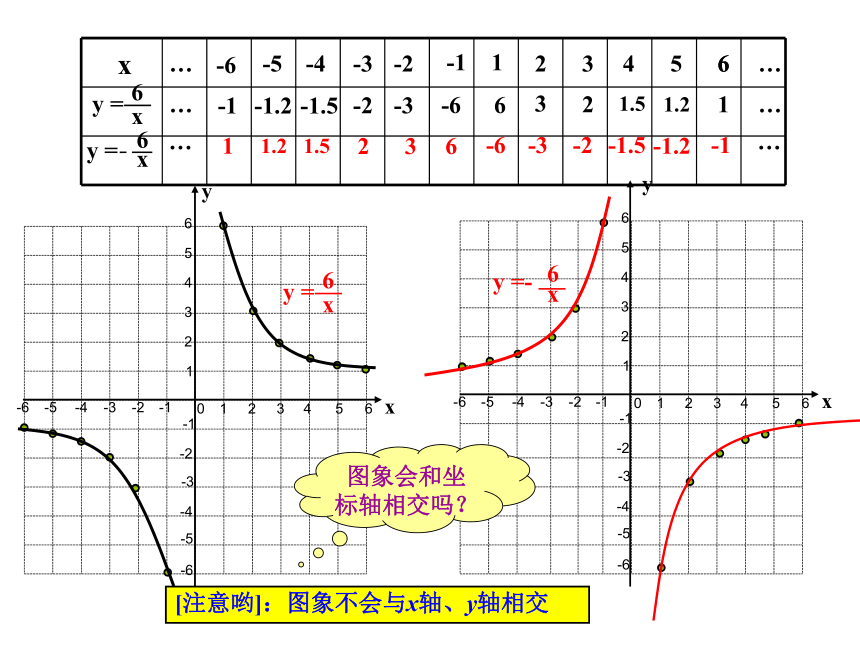
③选整数较好计算和描点。例 1123456-1-3-2-4-5-61234-1-2-3-40-6-556yx123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………-663-32-21.5-1.51.2-1.21-1……图象会和坐标轴相交吗?[注意哟]:图象不会与x轴、y轴相交你认为作反比例函数图象时应注意哪些问题?列表时,自变量的值可以选取一些互为相反数的值,这样既可简化计算,又便于对称性描点;
列表描点时,要尽量多取一些数值,多描一些点,这样既可以方便连线,又较准确地表达函数的变化趋势;
连线时一定要养成按自变量从小到大的顺序,依次用平滑的曲线连接,从中体会函数的增减性;
……“心动”不如行动操作: 函数图象画法列
表描
点连
线 描点法反比例函数的
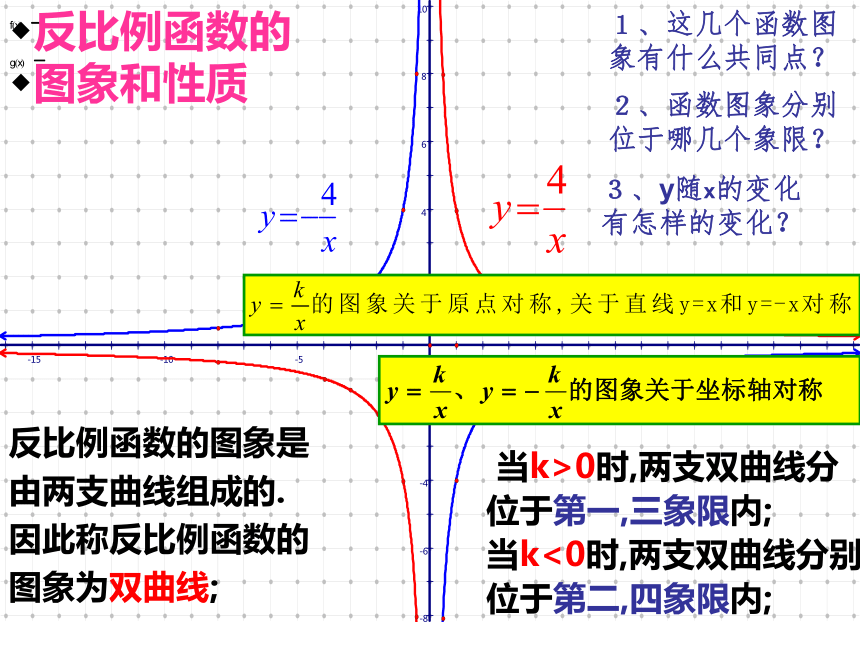
图象和性质反比例函数的图象是
由两支曲线组成的.
因此称反比例函数的
图象为双曲线; 当k>0时,两支双曲线分
位于第一,三象限内;
当k<0时,两支双曲线分别
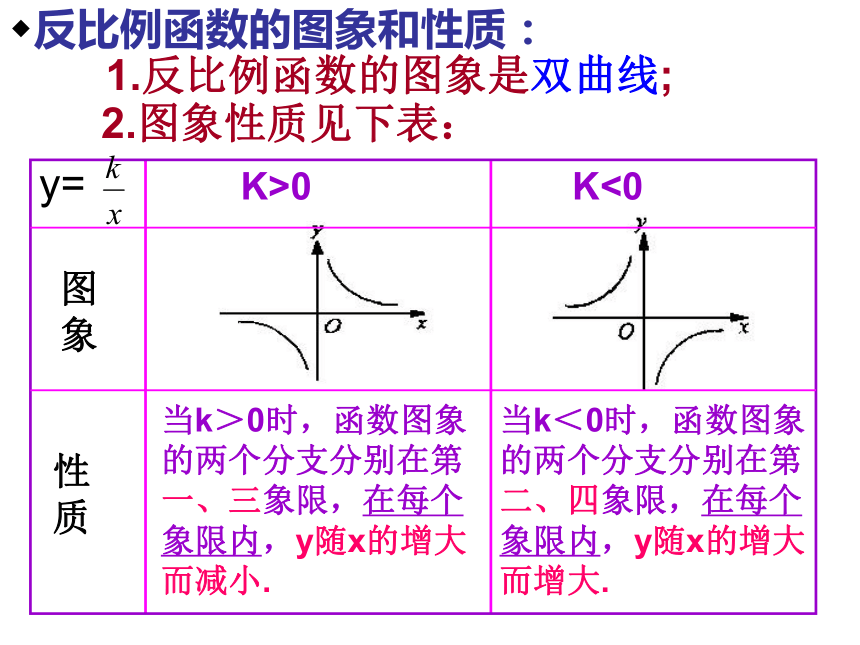
位于第二,四象限内;1、这几个函数图象有什么共同点?2、函数图象分别位于哪几个象限?3、y随x的变化有怎样的变化?K>0K<0当k>0时,函数图象
的两个分支分别在第
一、三象限,在每个
象限内,y随x的增大
而减小.
当k<0时,函数图象
的两个分支分别在第
二、四象限,在每个
象限内,y随x的增大
而增大.
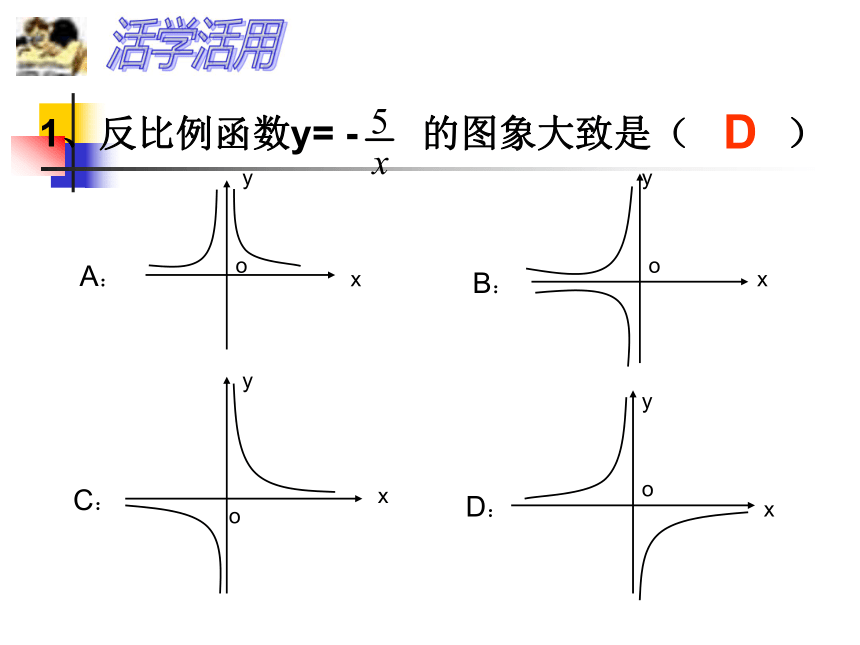
1.反比例函数的图象是双曲线; 2.图象性质见下表:反比例函数的图象和性质:D活学活用CD1、函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
2、 函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
3、函数 ,当x>0时,图象在第____象限,
y随x 的增大而_________.
一、三二、四一减小增大减小1、已知反比例函数
若函数的图象位于第一三象限, 则k______;
若在每一象限内,y随x增大而增大, 则k______.< 4> 42. 反比例函数 (K为常数)图象位于( )
A.第一、二象限 B.第一、三象限
C.第二、四象限 D.第三、四象限C 1、已知反比例函数 的函数图象位于第一、三象限,
则m的取值范围是 。m<2会自编类似问题吗?①②反馈练习:如: 若函数 是反比例函数,且图象位于第一、三象限,则m的值为 。m=26、 下列函数中,其图象位于第二、四象限的有 ,
在其图象所在的象限内,y随x的增大而减小的有 。7、正比例函数y=x与反比例函数 图象交点有 个, 正比例函数y=x与反比例函数 图象交点有 个。5、任意写出一个在每一个象限内y随x的增大而减小的反比例函数 。(只需k>0)(1),(4)(2),(3)两零 1 已知圆柱的侧面积是10πcm2,若圆柱底面半径为rcm,高为hcm,则h与r的函数图象大致是( ).C 函数y=kx-k 与 在同一条直角坐标系中的 图象可能是 :DB例2 已知反比例函数的图象经过点(2,6)
(1)这个函数的图象位于哪些象限?y随x的增大如何变化?
(2)点B(3,4), D(2,5)是否在这个函数的图象上?例题讲解拓展提升11、若点(-2,y1)、(-1,y2)、(2,y3)在
反比例函数 的图象上,则( )A、y1>y2>y3 B、y2>y1>y3
C、y3>y1>y2 D、y3>y2>y1B(A)图像位于同样的象限 (B)自变量取值是全体实数
(C)图像都不与坐标轴相交 (D)函数值都大于0( )C 考察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .-1-102.如图是三个反比例函数在x轴上方的图像, 由此观察得到( )
A k1>k2>k3 B k3>k2>k1
C k2>k1>k3 D k3>k1>k21k2k3B 练 习 1. 已知k<0,则函数 y1=kx,y2= 在同一坐标系中的图象大致是 ( )2. 已知k>0,则函数 y1=kx+k与y2= 在同一坐标系中
的图象大致是 ( )3.设x为一切实数,在下列函数中,当x减小时,y的值总是增大的函数是( )(A) y = -5x -1 ( B)y = (C)y=-2x+2; (D)y=4x.DCC5.点(23,-3)在反比例函数y=k/x的图象上,则k=______。
该函数的图象位于第_______象限,y随x增大而_______,若点
P(a, 2)是该函数上的一点,则a=_______.6.反比例函数y=k2/x( x<0)的图象位于_______象限。y随x增大而________.7.若点A ( 1, a), B(2,b), C(-3, c)在反比例函数
y=1/x 的图象上,则__________(判断a,b,c的大小关系)。8.已知反比例函数y =m+1 / x 的图象在所在象限内y随x
增大而增大,则m的取值范围是___________.-69增大-69/2三减小a>b>cm<-1二,四①如果y与z成正比例, z 与x成正比例,则 y 与x 的函数关系是: ③如果y与z成反比例, z 与x成正比例,则 y 与x 的函数关系是: 练 习12②如果y与z成正比例, z 与x成反比例,则 y 与x 的函数关系是: ④如果y与z成反比例, z 与x成反比例,则 y 与x 的函数关系是: Y与x成正比例Y与x成反比例Y与x成反比例Y与x成正比例课堂小结:反比例函数 (k为常数,k≠0)双曲线图象性质k>0k<0双曲线的两支所在象限在每个象限内的增减性内容1、进一步巩固复习了作函数图象的一般方法和步骤2、亲手画出函数的图象,用类比的方法,数形结合的思想,有了对图形进行观察、分析和归纳的体验,掌握了反比例函数的图象和性质当k>0时,双曲线的两支分别位于第一、第三象限, 在每个象限内y值随x值的增大而减小。当k<0时,双曲线的两支分别位于第二、第四象限, 在每个象限内y值随x值的增大而增大。
反比例函数的图象和性质(1)(2)你还记得正比例函数y=kx (k≠0)的图像和性质吗?温故导新(1)根据上节课的学习,说说你记忆中的反比例函数.挑战“记忆”你还记得一次函数的图象与性质吗?一次函数y=kx+b(k≠0)的图象是一条直线,
称直线y=kx+b.y随x的增大而增大;y随x的增大而减小.当k>0时,当k<0时,位置增减性位置增减性y=kx ( k≠0 ) 直线一、三象限从左到右上升
y随x的增大而增大二、四象限 从左到右下降
y随x的增大而减小
反比例函数?正比例函数y=kx (k≠0)的图像的位置和增减性是由谁决定的?我们是如何探究得到的?
“预见性”,猜一猜反比例函数的图象又会是什么样子呢?你还记得作函数图象的一般步骤吗?用图象法表示函数关系时,首先在自变量的取值范围内取一些值,列表,描点,连线(按自变量从小到大的顺序,用一条平滑的曲线连接起来). 函数图象画法列
表描
点连
线 描点法注意:①列表时自变量
取值要均匀和对称②x≠0
③选整数较好计算和描点。例 1123456-1-3-2-4-5-61234-1-2-3-40-6-556yx123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………-663-32-21.5-1.51.2-1.21-1……图象会和坐标轴相交吗?[注意哟]:图象不会与x轴、y轴相交你认为作反比例函数图象时应注意哪些问题?列表时,自变量的值可以选取一些互为相反数的值,这样既可简化计算,又便于对称性描点;
列表描点时,要尽量多取一些数值,多描一些点,这样既可以方便连线,又较准确地表达函数的变化趋势;
连线时一定要养成按自变量从小到大的顺序,依次用平滑的曲线连接,从中体会函数的增减性;
……“心动”不如行动操作: 函数图象画法列
表描
点连
线 描点法反比例函数的
图象和性质反比例函数的图象是
由两支曲线组成的.
因此称反比例函数的
图象为双曲线; 当k>0时,两支双曲线分
位于第一,三象限内;
当k<0时,两支双曲线分别
位于第二,四象限内;1、这几个函数图象有什么共同点?2、函数图象分别位于哪几个象限?3、y随x的变化有怎样的变化?K>0K<0当k>0时,函数图象
的两个分支分别在第
一、三象限,在每个
象限内,y随x的增大
而减小.
当k<0时,函数图象
的两个分支分别在第
二、四象限,在每个
象限内,y随x的增大
而增大.
1.反比例函数的图象是双曲线; 2.图象性质见下表:反比例函数的图象和性质:D活学活用CD1、函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
2、 函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
3、函数 ,当x>0时,图象在第____象限,
y随x 的增大而_________.
一、三二、四一减小增大减小1、已知反比例函数
若函数的图象位于第一三象限, 则k______;
若在每一象限内,y随x增大而增大, 则k______.< 4> 42. 反比例函数 (K为常数)图象位于( )
A.第一、二象限 B.第一、三象限
C.第二、四象限 D.第三、四象限C 1、已知反比例函数 的函数图象位于第一、三象限,
则m的取值范围是 。m<2会自编类似问题吗?①②反馈练习:如: 若函数 是反比例函数,且图象位于第一、三象限,则m的值为 。m=26、 下列函数中,其图象位于第二、四象限的有 ,
在其图象所在的象限内,y随x的增大而减小的有 。7、正比例函数y=x与反比例函数 图象交点有 个, 正比例函数y=x与反比例函数 图象交点有 个。5、任意写出一个在每一个象限内y随x的增大而减小的反比例函数 。(只需k>0)(1),(4)(2),(3)两零 1 已知圆柱的侧面积是10πcm2,若圆柱底面半径为rcm,高为hcm,则h与r的函数图象大致是( ).C 函数y=kx-k 与 在同一条直角坐标系中的 图象可能是 :DB例2 已知反比例函数的图象经过点(2,6)
(1)这个函数的图象位于哪些象限?y随x的增大如何变化?
(2)点B(3,4), D(2,5)是否在这个函数的图象上?例题讲解拓展提升11、若点(-2,y1)、(-1,y2)、(2,y3)在
反比例函数 的图象上,则( )A、y1>y2>y3 B、y2>y1>y3
C、y3>y1>y2 D、y3>y2>y1B(A)图像位于同样的象限 (B)自变量取值是全体实数
(C)图像都不与坐标轴相交 (D)函数值都大于0( )C 考察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .-1-1
A k1>k2>k3 B k3>k2>k1
C k2>k1>k3 D k3>k1>k21k2k3B 练 习 1. 已知k<0,则函数 y1=kx,y2= 在同一坐标系中的图象大致是 ( )2. 已知k>0,则函数 y1=kx+k与y2= 在同一坐标系中
的图象大致是 ( )3.设x为一切实数,在下列函数中,当x减小时,y的值总是增大的函数是( )(A) y = -5x -1 ( B)y = (C)y=-2x+2; (D)y=4x.DCC5.点(23,-3)在反比例函数y=k/x的图象上,则k=______。
该函数的图象位于第_______象限,y随x增大而_______,若点
P(a, 2)是该函数上的一点,则a=_______.6.反比例函数y=k2/x( x<0)的图象位于_______象限。y随x增大而________.7.若点A ( 1, a), B(2,b), C(-3, c)在反比例函数
y=1/x 的图象上,则__________(判断a,b,c的大小关系)。8.已知反比例函数y =m+1 / x 的图象在所在象限内y随x
增大而增大,则m的取值范围是___________.-69增大-69/2三减小a>b>cm<-1二,四①如果y与z成正比例, z 与x成正比例,则 y 与x 的函数关系是: ③如果y与z成反比例, z 与x成正比例,则 y 与x 的函数关系是: 练 习12②如果y与z成正比例, z 与x成反比例,则 y 与x 的函数关系是: ④如果y与z成反比例, z 与x成反比例,则 y 与x 的函数关系是: Y与x成正比例Y与x成反比例Y与x成反比例Y与x成正比例课堂小结:反比例函数 (k为常数,k≠0)双曲线图象性质k>0k<0双曲线的两支所在象限在每个象限内的增减性内容1、进一步巩固复习了作函数图象的一般方法和步骤2、亲手画出函数的图象,用类比的方法,数形结合的思想,有了对图形进行观察、分析和归纳的体验,掌握了反比例函数的图象和性质当k>0时,双曲线的两支分别位于第一、第三象限, 在每个象限内y值随x值的增大而减小。当k<0时,双曲线的两支分别位于第二、第四象限, 在每个象限内y值随x值的增大而增大。
