26.1.2 反比例函数的图象和性质(1) 课件
文档属性
| 名称 | 26.1.2 反比例函数的图象和性质(1) 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 829.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-02 00:00:00 | ||
图片预览





文档简介
课件29张PPT。26.1.2 反比例函数的
图 象 和 性 质(1)1.进一步熟悉作函数图象的步骤,会画反比例函数的图象.
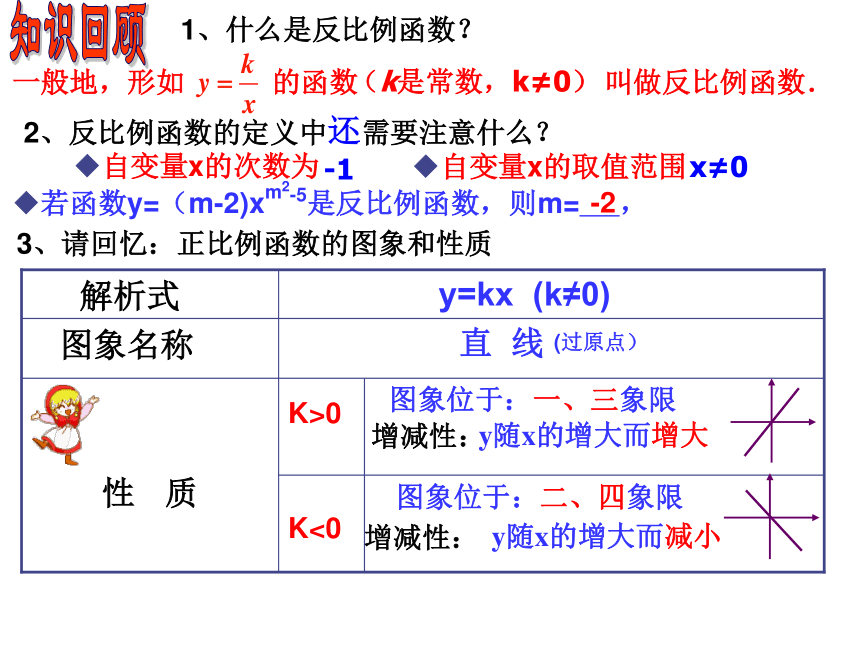
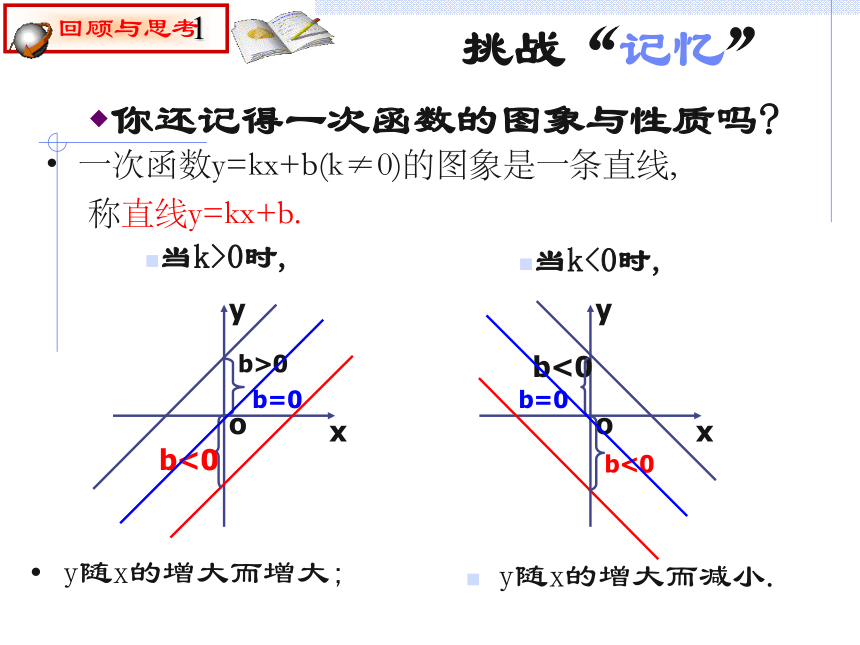
2.体会函数的三种表示方法的相互转换,逐步提高从函数图象获取信息的能力,探索并掌握反比例函数的主要性质.知识回顾1、什么是反比例函数? 2、反比例函数的定义中还需要注意什么?◆自变量x的取值范围◆自变量x的次数为 3、请回忆:正比例函数的图象和性质-2 (k是常数,k≠0)-1x≠0◆若函数y=(m-2)xm2-5是反比例函数,则m= , 挑战“记忆”你还记得一次函数的图象与性质吗?一次函数y=kx+b(k≠0)的图象是一条直线,
称直线y=kx+b.y随x的增大而增大;y随x的增大而减小.当k>0时,当k<0时,研究反比例函数的图象和性质1、列表2、描点3、连线画函数图象的一般步骤:y123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………你认为作反比例函数图象时应注意哪些问题?列表时,自变量的值可以选取一些互为相反数的值,这样既可简化计算,又便于对称性描点;
列表描点时,要尽量多取一些数值,多描一些点,这样既可以方便连线,又较准确地表达函数的变化趋势;
连线时一定要养成按自变量从小到大的顺序,依次用平滑的曲线连接,从中体会函数的增减性;
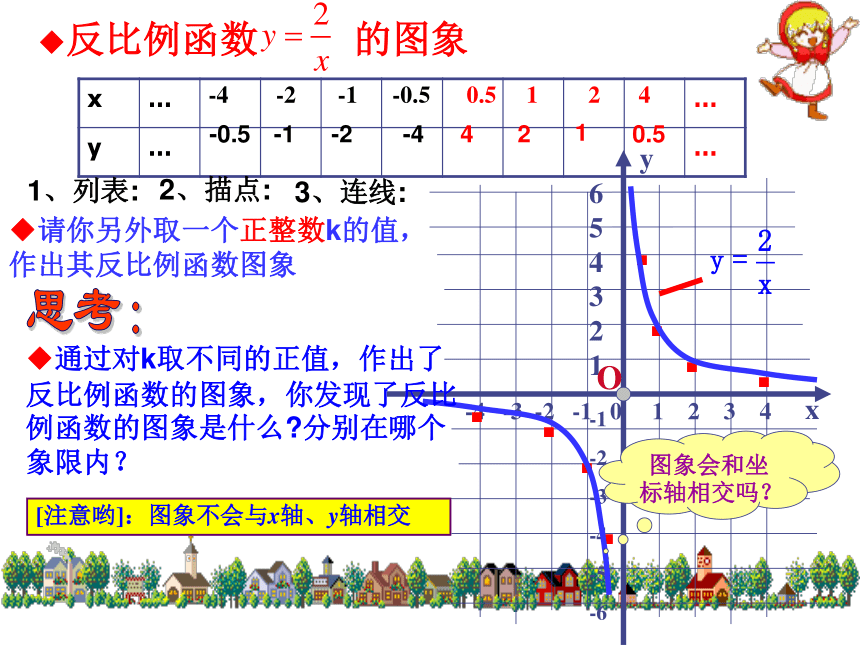
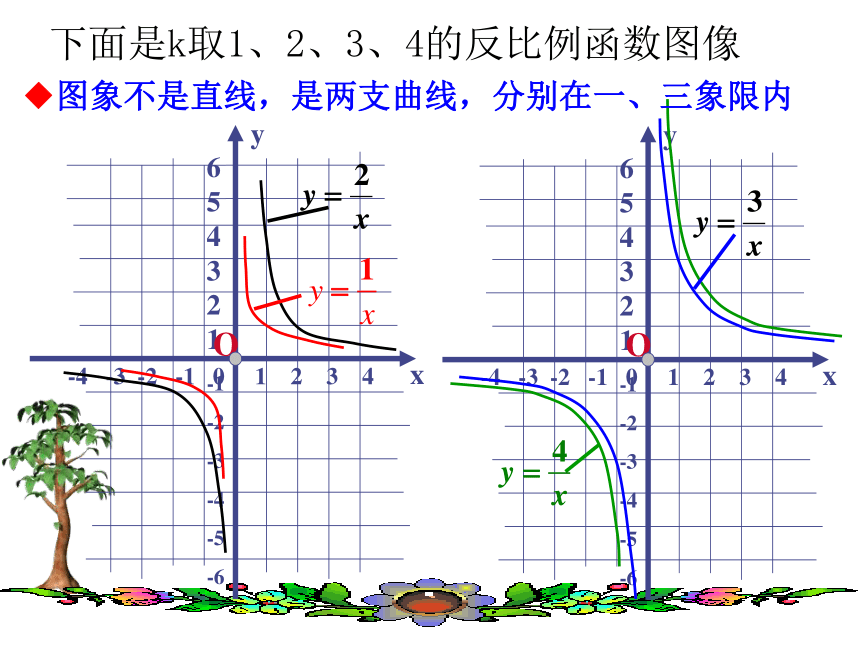
……◆反比例函数 的图象1、列表:2、描点:3、连线:········-0.5-1-2-44210.5◆请你另外取一个正整数k的值,作出其反比例函数图象图象会和坐标轴相交吗?◆通过对k取不同的正值,作出了反比例函数的图象,你发现了反比例函数的图象是什么?分别在哪个象限内?思考:-4 -2 -1 -0.5 0.5 1 2 4[注意哟]:图象不会与x轴、y轴相交◆图象不是直线,是两支曲线,分别在一、三象限内123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………◆图象由两条曲线组成,叫做双曲线,◆只要k取正值,图象都位于第一、三象限内◆K的值还可以取其他一些什么值?说说看①列表、描点、连线②对称性123456-1-3-2-4-5-61234-1-2-3-40-6-556yx123456-1-3-2-4-5-61234-1-2-3-40-6-556xy发现函数值y怎样随着自变量x的变化而变化?·AB·如图xB< xA但yB< yAD·C·xAxB1、在每一个象限内2、在整个自变量的取值范围内在每个象限内在每个象限内yXOk>0K<0反比例函数的图象和性质双曲线的两支分别双曲线的两支分别双曲线k>0k<0位于第一、第三象限,位于第二、第四象限,y值随x值的增大而减小。y值随x值的增大而增大。1、反比例函数 (k为常数,k≠0)
的图象是双曲线2、当k>0时,双曲线的两支分别位于第一、第三象限, 在每个象限内y值随x值的增大而减小。3、当k<0时,双曲线的两支分别位于第二、第四象限, 在每个象限内y值随x值的增大而增大。K>0K<0当k>0时,函数图象
的两个分支分别在第
一、三象限,在每个
象限内,y随x的增大
而减小.
当k<0时,函数图象
的两个分支分别在第
二、四象限,在每个
象限内,y随x的增大
而增大.
1.反比例函数的图象是双曲线; 2.图象性质见下表:反比例函数的图象和性质:D活学活用1、函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
2、 函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
3、函数 ,当x>0时,图象在第____象限,
y随x 的增大而_________.
一、三二、四一减小增大减小已知反比例函数
若函数的图象位于第一三象限,
则k_____________;
若在每一象限内,y随x增大而增大,
则k_____________.< 4> 4 函数y=kx-k 与 在同一条直角坐标系中的 图象可能是 :D 考察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .-1-10若点(-2,y1)、(-1,y2)、(2,y3)在
反比例函数 的图象上,则( )A、y1>y2>y3 B、y2>y1>y3
C、y3>y1>y2 D、y3>y2>y1B 已知圆柱的侧面积是10πcm2,若圆柱底面半径为rcm,高为hcm,则h与r的函数图象大致是( ).Cm<23、下列反比例函数图像的一个分支,在第三象限的是( )二、四B2、 下列函数中,其图象位于第二、四象限的有 ,
在其图象所在的象限内,y随x的减小而增大的有 。(1),(4)(2),(3)解:不一定y1>y2则y1>y2则y1 2.你对自己本节课的表现满意吗?为什么?及时小结,自我评价数缺形时少直觉,形少数时难入微.1、进一步巩固复习了作函数图象的一般方法和步骤2、亲手画出函数的图象,用类比的方法,数形结合的思想,有了对图形进行观察、分析和归纳的体验,掌握了反比例函数的图象和性质当k>0时,双曲线的两支分别位于第一、第三象限, 在每个象限内y值随x值的增大而减小。当k<0时,双曲线的两支分别位于第二、第四象限, 在每个象限内y值随x值的增大而增大。作业:课本46页第3、8题和课本60页第10题3.已知反比例函数 的图象在
第二、四象限,那么一次函数y=kx-k的图象经过( )A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限C4.甲乙两地相距100km,一辆汽车从甲地开往乙地,把汽
车到达乙地所用的时间y(h)表示为汽车的平均速度x(km/h)
的函数,则这个函数的图象大致是( )C提示:在实际问题中图象只有一支曲线. 7、考察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .-1-105.若关于x,y的函数 图象位于第一、三象限,
则k的取值范围是_________.k>-1
图 象 和 性 质(1)1.进一步熟悉作函数图象的步骤,会画反比例函数的图象.
2.体会函数的三种表示方法的相互转换,逐步提高从函数图象获取信息的能力,探索并掌握反比例函数的主要性质.知识回顾1、什么是反比例函数? 2、反比例函数的定义中还需要注意什么?◆自变量x的取值范围◆自变量x的次数为 3、请回忆:正比例函数的图象和性质-2 (k是常数,k≠0)-1x≠0◆若函数y=(m-2)xm2-5是反比例函数,则m= , 挑战“记忆”你还记得一次函数的图象与性质吗?一次函数y=kx+b(k≠0)的图象是一条直线,
称直线y=kx+b.y随x的增大而增大;y随x的增大而减小.当k>0时,当k<0时,研究反比例函数的图象和性质1、列表2、描点3、连线画函数图象的一般步骤:y123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………你认为作反比例函数图象时应注意哪些问题?列表时,自变量的值可以选取一些互为相反数的值,这样既可简化计算,又便于对称性描点;
列表描点时,要尽量多取一些数值,多描一些点,这样既可以方便连线,又较准确地表达函数的变化趋势;
连线时一定要养成按自变量从小到大的顺序,依次用平滑的曲线连接,从中体会函数的增减性;
……◆反比例函数 的图象1、列表:2、描点:3、连线:········-0.5-1-2-44210.5◆请你另外取一个正整数k的值,作出其反比例函数图象图象会和坐标轴相交吗?◆通过对k取不同的正值,作出了反比例函数的图象,你发现了反比例函数的图象是什么?分别在哪个象限内?思考:-4 -2 -1 -0.5 0.5 1 2 4[注意哟]:图象不会与x轴、y轴相交◆图象不是直线,是两支曲线,分别在一、三象限内123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………◆图象由两条曲线组成,叫做双曲线,◆只要k取正值,图象都位于第一、三象限内◆K的值还可以取其他一些什么值?说说看①列表、描点、连线②对称性123456-1-3-2-4-5-61234-1-2-3-40-6-556yx123456-1-3-2-4-5-61234-1-2-3-40-6-556xy发现函数值y怎样随着自变量x的变化而变化?·AB·如图xB< xA但yB< yAD·C·xAxB1、在每一个象限内2、在整个自变量的取值范围内在每个象限内在每个象限内yXOk>0K<0反比例函数的图象和性质双曲线的两支分别双曲线的两支分别双曲线k>0k<0位于第一、第三象限,位于第二、第四象限,y值随x值的增大而减小。y值随x值的增大而增大。1、反比例函数 (k为常数,k≠0)
的图象是双曲线2、当k>0时,双曲线的两支分别位于第一、第三象限, 在每个象限内y值随x值的增大而减小。3、当k<0时,双曲线的两支分别位于第二、第四象限, 在每个象限内y值随x值的增大而增大。K>0K<0当k>0时,函数图象
的两个分支分别在第
一、三象限,在每个
象限内,y随x的增大
而减小.
当k<0时,函数图象
的两个分支分别在第
二、四象限,在每个
象限内,y随x的增大
而增大.
1.反比例函数的图象是双曲线; 2.图象性质见下表:反比例函数的图象和性质:D活学活用1、函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
2、 函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
3、函数 ,当x>0时,图象在第____象限,
y随x 的增大而_________.
一、三二、四一减小增大减小已知反比例函数
若函数的图象位于第一三象限,
则k_____________;
若在每一象限内,y随x增大而增大,
则k_____________.< 4> 4 函数y=kx-k 与 在同一条直角坐标系中的 图象可能是 :D 考察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .-1-1
反比例函数 的图象上,则( )A、y1>y2>y3 B、y2>y1>y3
C、y3>y1>y2 D、y3>y2>y1B 已知圆柱的侧面积是10πcm2,若圆柱底面半径为rcm,高为hcm,则h与r的函数图象大致是( ).Cm<23、下列反比例函数图像的一个分支,在第三象限的是( )二、四B2、 下列函数中,其图象位于第二、四象限的有 ,
在其图象所在的象限内,y随x的减小而增大的有 。(1),(4)(2),(3)解:不一定y1>y2则y1>y2则y1
第二、四象限,那么一次函数y=kx-k的图象经过( )A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限C4.甲乙两地相距100km,一辆汽车从甲地开往乙地,把汽
车到达乙地所用的时间y(h)表示为汽车的平均速度x(km/h)
的函数,则这个函数的图象大致是( )C提示:在实际问题中图象只有一支曲线. 7、考察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .-1-1
则k的取值范围是_________.k>-1
