26.1.2 反比例函数的图象和性质强化练习 课件
文档属性
| 名称 | 26.1.2 反比例函数的图象和性质强化练习 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 333.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-02 11:14:40 | ||
图片预览




文档简介
课件20张PPT。26.1.2 反比例函数的图象和性质
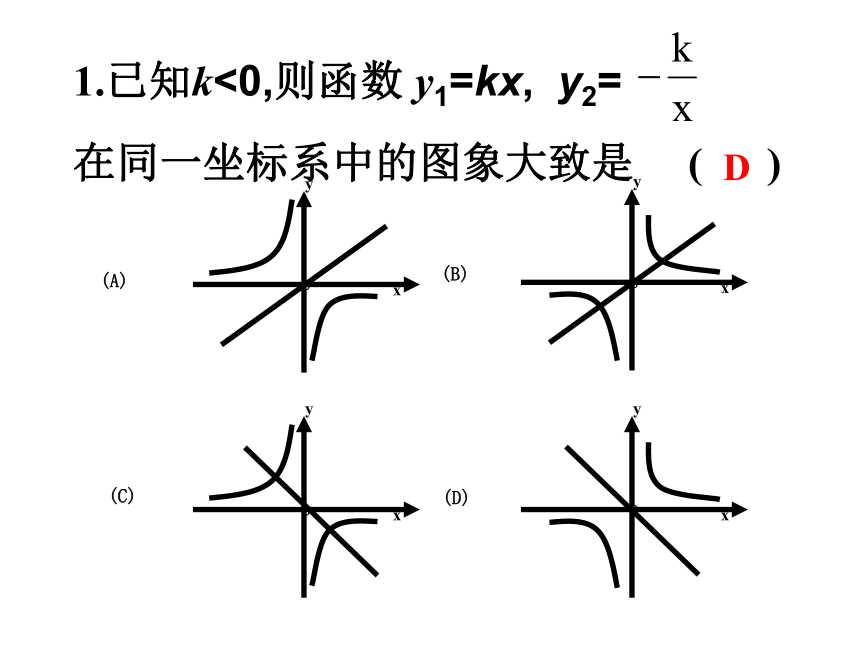
强化练习填一填反比例双曲线2x≠ 0一、三减小>一二、四增大<四已知k<0,则函数 y1=kx, y2=
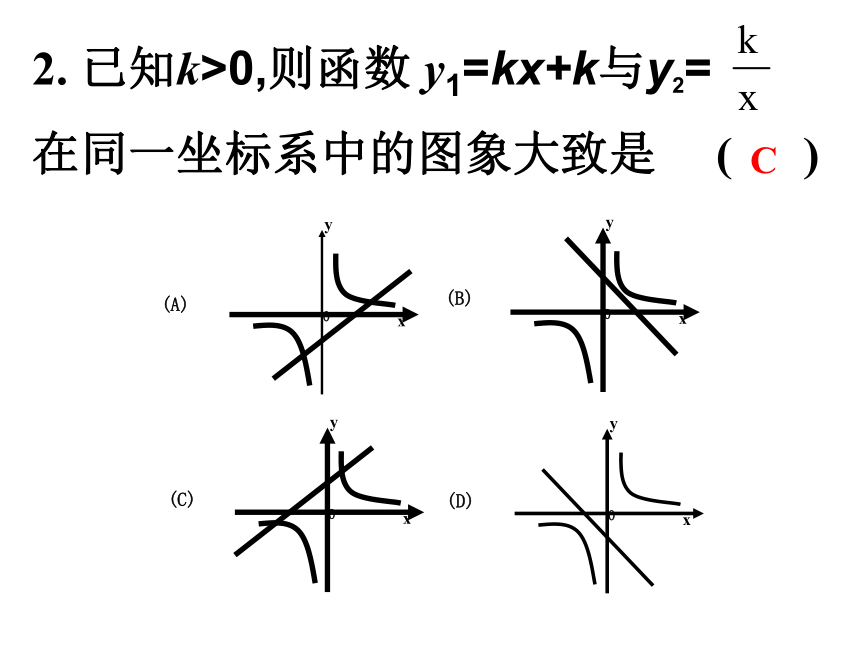
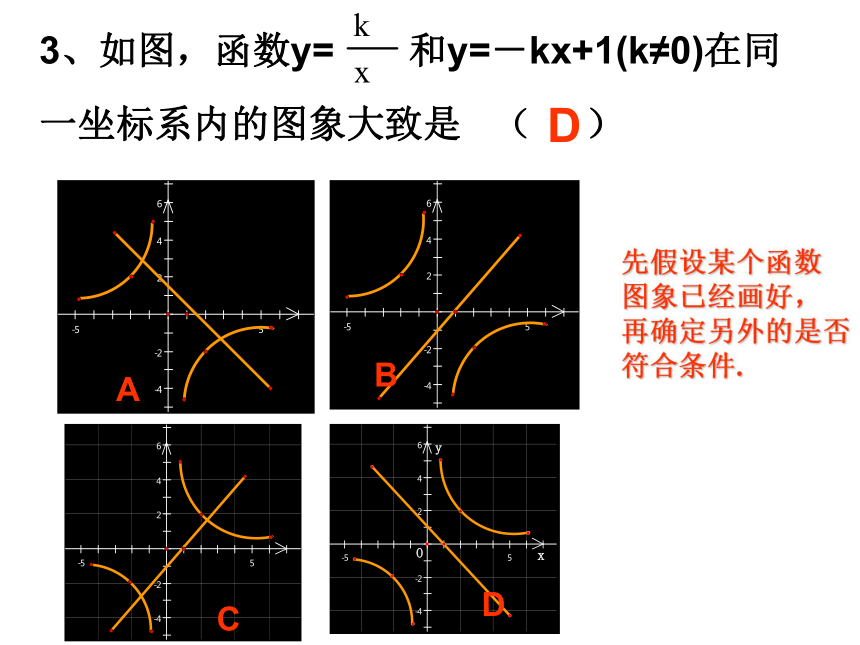
在同一坐标系中的图象大致是 ( )D2. 已知k>0,则函数 y1=kx+k与y2= 在同一坐标系中的图象大致是 ( )CBACDD先假设某个函数
图象已经画好,
再确定另外的是否
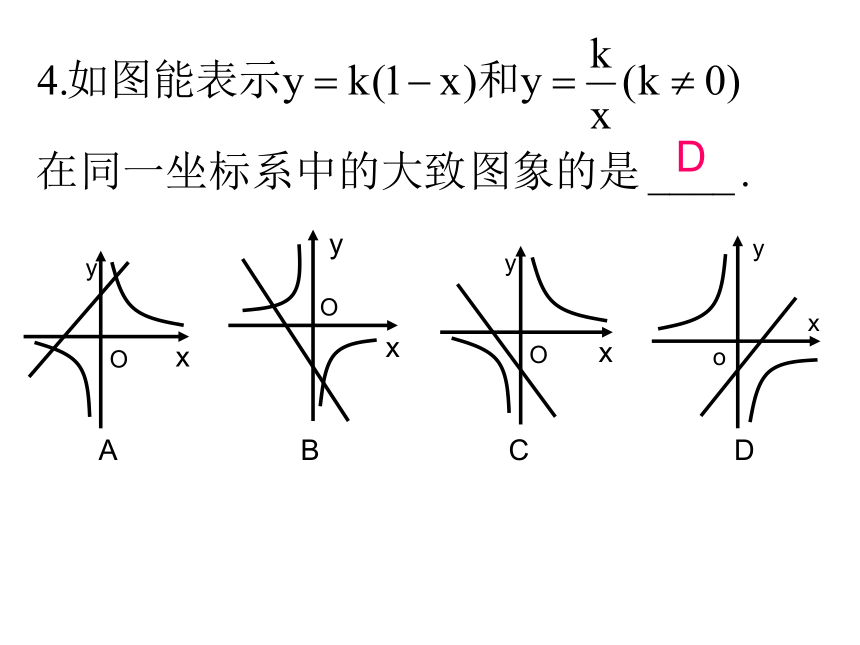
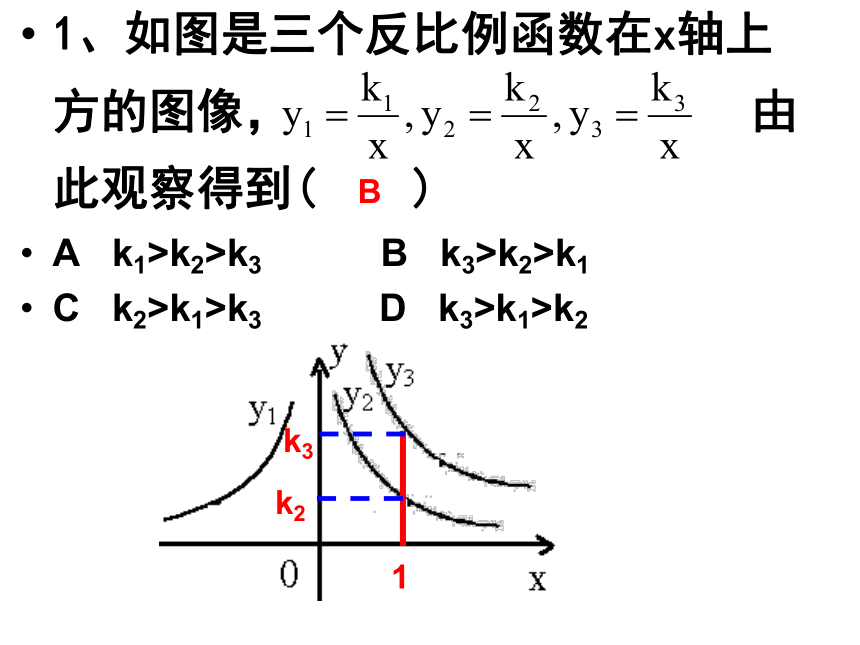
符合条件.D1、如图是三个反比例函数在x轴上方的图像, 由此观察得到( )
A k1>k2>k3 B k3>k2>k1
C k2>k1>k3 D k3>k1>k21k2k3B2.表示下面四个关系式的图像有图像与性质 2.如图:一次函数y=ax+b的图象与反比例函数
y= 交于M (2,m) 、N (-1,-4)两点
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出反比例函数的值大于一次函数的值的x的取值范围。N(-1,-4)M(2,m)(3)利用图象直接写出当x在什么范围内取何值时,y1>y2.(2)求出点D的坐标;(1)分别求直线AB与双曲线的解析式;如图,已知一次函数y=kx+b(k≠0)的图象与
x轴.y轴分别交于A.B两点,且与反比例函数
y=m/x(m≠0)的图象在第一象限内交于C点,CD
垂直于x轴,垂足为点D,若OA=OB=OD=1.
(1)求点A.B.D的坐标;
(2)求一次函数和
反比例函数的解析式D学以致用例:王先生驾车从A地前往300km外的B地,他的车速平均每小时v(km),A地到B地的时间为t(h)。
(1)以时间为横轴,速度为纵轴,画出反映v、t之间的变化关系的图象。
(2)观察图象,回答:①当v>100时,t的取值范围是什么?②如果平均速度控制在第每小时60km至每小时150km之间,王先生到达B地至少花费多少小时?(05江西省中考题)已知甲,乙两地相距skm,汽车从甲地匀速行驶到乙地.如果汽车每小时耗油量为aL,那么从甲地到乙地的总耗油量y(L)与汽车的行驶速度v(km/h)的函数图象大致是( ).实际应用反比例函数的图象既是轴对称图形又是中心对称图形。
有两条对称轴:直线y=x和 y=-x。对称中心是:原点xy012求(1)一次函数的解析式
(2)根据图像写出使一 次函数的值小于反比例函数的值的x的取值范围。
强化练习填一填反比例双曲线2x≠ 0一、三减小>一二、四增大<四已知k<0,则函数 y1=kx, y2=
在同一坐标系中的图象大致是 ( )D2. 已知k>0,则函数 y1=kx+k与y2= 在同一坐标系中的图象大致是 ( )CBACDD先假设某个函数
图象已经画好,
再确定另外的是否
符合条件.D1、如图是三个反比例函数在x轴上方的图像, 由此观察得到( )
A k1>k2>k3 B k3>k2>k1
C k2>k1>k3 D k3>k1>k21k2k3B2.表示下面四个关系式的图像有图像与性质 2.如图:一次函数y=ax+b的图象与反比例函数
y= 交于M (2,m) 、N (-1,-4)两点
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出反比例函数的值大于一次函数的值的x的取值范围。N(-1,-4)M(2,m)(3)利用图象直接写出当x在什么范围内取何值时,y1>y2.(2)求出点D的坐标;(1)分别求直线AB与双曲线的解析式;如图,已知一次函数y=kx+b(k≠0)的图象与
x轴.y轴分别交于A.B两点,且与反比例函数
y=m/x(m≠0)的图象在第一象限内交于C点,CD
垂直于x轴,垂足为点D,若OA=OB=OD=1.
(1)求点A.B.D的坐标;
(2)求一次函数和
反比例函数的解析式D学以致用例:王先生驾车从A地前往300km外的B地,他的车速平均每小时v(km),A地到B地的时间为t(h)。
(1)以时间为横轴,速度为纵轴,画出反映v、t之间的变化关系的图象。
(2)观察图象,回答:①当v>100时,t的取值范围是什么?②如果平均速度控制在第每小时60km至每小时150km之间,王先生到达B地至少花费多少小时?(05江西省中考题)已知甲,乙两地相距skm,汽车从甲地匀速行驶到乙地.如果汽车每小时耗油量为aL,那么从甲地到乙地的总耗油量y(L)与汽车的行驶速度v(km/h)的函数图象大致是( ).实际应用反比例函数的图象既是轴对称图形又是中心对称图形。
有两条对称轴:直线y=x和 y=-x。对称中心是:原点xy012求(1)一次函数的解析式
(2)根据图像写出使一 次函数的值小于反比例函数的值的x的取值范围。
