4.3 平行线的性质同步练习
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
4.3 平行线的性质同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.平行线的性质1:两条平行直线被第三条直线所截,同位角相等.可简说成两直线平行,同位角相等.
2.平行线的性质2:两条平行直线被第三条直线所截,内错角相等.可简说成两直线平行,内错角相等.
3.平行线的性质3:两条平行直线被第三条直线所截,同旁内角互补.可简说成两直线平行,同旁内角互补 .
基础知识和能力拓展精练
一、选择题
1.如图,已知∠AOB=70°,OC平分∠AOB,DC∥OB,则∠C为( )
A. 20° B. 35° C. 45° D. 70°
2.如图, 下列各式中正确的是( )
A. B.
C. D.
3.如图,如果AB∥CD,那么图中相等的内错角是( )
A. ∠1与∠5,∠2与∠6; B. ∠3与∠7,∠4与∠8;
C. ∠5与∠1,∠4与∠8; D. ∠2与∠6,∠7与∠3
4.如图,AC∥DF,AB∥EF,若∠2=50°,则∠1的大小是( )
A. 60° B. 50° C. 40° D. 30°
5.如图,AB∥CD,EF交AB、CD于点E、F,EG平分∠BEF,交CD于点G.若∠1=40°,则∠EGF=( )
A. 20° B. 40° C. 70° D. 110°
6.如图,将三角板的直角顶点放在直尺的一边上,若,则的度数为( )
A. B. C. D.
7.如图所示,下列推理不正确的是( ).
A. 若,则 B. 若,则
C. 若,则 D. 若,则
8.如图,由AC∥ED,可知相等的角有( )
A. 6对 B. 5对 C. 4对 D. 3对
二、填空题
9.如图为某条公路的示意图,两次拐弯后和原来的方向相同,即拐弯前后的两条路互相平行,第一次拐的角为∠M=150°,则第二次拐的角∠N=_________.
10.如图,直线a∥b,直线a,b被直线c所截,∠1=37°,则∠2=________.
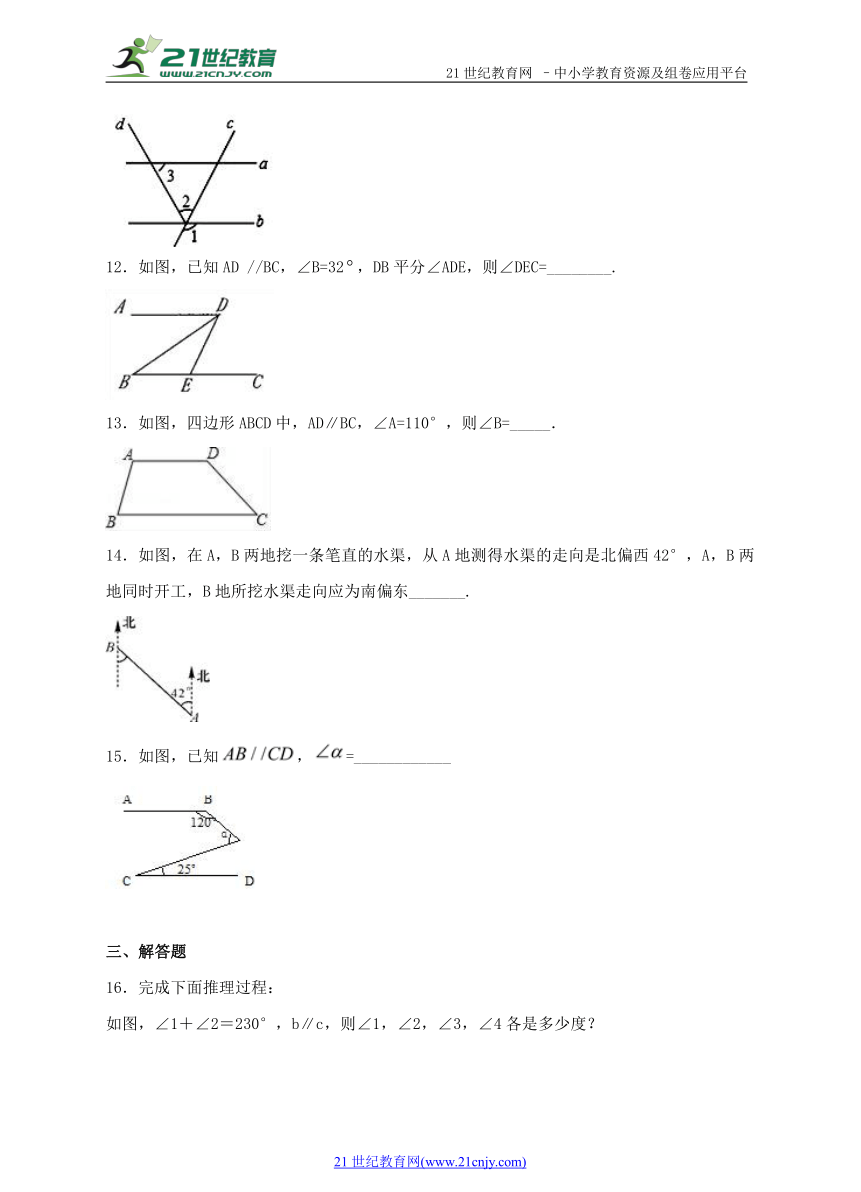
11.如图,a∥b,∠1=110°,∠3=40°,则∠2=_________°
12.如图,已知AD //BC,∠B=32,DB平分∠ADE,则∠DEC=________.
13.如图,四边形ABCD中,AD∥BC,∠A=110°,则∠B=_____.
14.如图,在A,B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42°,A,B两地同时开工,B地所挖水渠走向应为南偏东_______.
15.如图,已知,=____________
三、解答题
16.完成下面推理过程:
如图,∠1+∠2=230°,b∥c,则∠1,∠2,∠3,∠4各是多少度?
解:∵∠1=∠2(__________________),
∠1+∠2=230°,
∴∠1=∠2=___________(填度数).
∵b∥c,
∴∠4=∠2=_______(填度数)(_______________________________),
∠2+∠3=180°(________________________________),
∴∠3=180°-∠2=____________(填度数).
17.如图,直线,求证: .
18.如图,AB∥CD,∠1=∠2,∠BDF与 ∠EFC相等吗?为什么?
19.已知:如图,AB∥DE,CM平分∠BCE,CN⊥CM.求证:∠B=2∠DCN.
20.阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
参考答案
1.B
【解析】解:∵OC平分∠AOB,∴∠AOC=∠BOC=∠AOB=35°,∵CD∥OB,∴∠BOC=∠C=35°,故选B.
2.D
【解析】∵OP//QR//ST,∴∠2+∠PRQ=180°,∠3=∠SRQ=∠1+∠PRQ,
∴∠PRQ=180°-∠2,
∴∠3=∠1+180°-∠2,即∠2+∠3-∠1=180°.
故选D.
点睛:本题关键利用平行线的性质解题.
3.D
【解析】AB∥CD,所以∠2与∠6,∠7与∠3.故选D.
4.B
【解析】根据平行线的性质即可求解.
解:∵AC∥DF,
∴∠F=∠2=50°,
∵AB∥EF,
∴∠1=∠F=50°.
故选B.
5.C
【解析】∵∠1=40°,∴∠BEF=140°,
∵EG平分∠BEF,∴∠BEG=∠GEF=70°,
∵AB∥CD,∴∠BEG=∠EGF=70°.
故选C.
点睛:掌握平行线的性质以及角平分线的性质.
6.C
【解析】如图,因为AD∥BC,所以∠1=∠3=65°,因为∠2+∠3+90°=180°,所以∠2=90°-∠3=90°-65°=25°,故选C.
7.D
【解析】A. ∵∠1=∠C,∴AE ∥ CD( 同位角相等 , 两直线平行 ) ,故正确;
B. ∵∠2=∠BAE,∴AB ∥ DE( 内错角相等 , 两直线平行 ) ,故正确;
C. ∵∠B+∠BAD=180 ,∴AD ∥ BC( 同旁内角互补 , 两直线平行 ) ,故正确;
D. ∵∠C+∠ADC=180 ,∴AD ∥ BC( 同旁内角互补 , 两直线平行 ) ,故错误。
故选D.
8.B
【解析】试题解析:如图,
∵AC∥ED,
∴∠BED=∠BAC,∠FAC=∠FED,∠EDF=∠1,∠1=∠2,∠C=∠BDE.共5对.
故选B.
9.150°
【解析】∵AM∥BN,
∴∠AMN=∠BNM=150°.
故答案为150°.
10.143°
【解析】
∵a∥b,∴∠1=∠3=37°,∴∠2=180°-37°=143°.
故答案为143°.
11.70
【解析】试题解析:如图,
∵a∥b,∠3=40°,
∴∠4=∠3=40°.
∵∠1=∠2+∠4=110°,
∴∠2=110°-∠4=110°-40°=70°.
故答案为:70.
12.
【解析】∵AD //BC,
∴∠ADB=∠B=32°.
∵DB平分∠ADE,
∴∠ADB=∠EDB=∠B=32°,
∴∠ADE=32°+32°=64°,
∴∠DEC=∠ADE=64°.
13.70°
【解析】因为AD∥BC,所以∠A+∠B=180°,因为∠A=110°,所以∠B=70°,故答案为70°.
14.42°
【解析】试题解析:
因为两个北方向是平行的,即AC∥BD,
所以A点北偏西的角与B点南偏东的角是内错角,
因此它们都等于42°.
故答案为:42°.
15.
【解析】试题解析:如图,
过E点作EF∥AB,
∵AB∥CD
∴EF∥AB∥CD
∴∠ABE+∠FEB=180°
∠DCE=∠FEC
∵∠ABE=120°, ∠DCE=25°
∴∠BEF=60°∠FEC=25°
∴∠a=60°+25°=85°
16.对顶角相等;115°;115°;两直线平行,内错角相等;两直线平行,同旁内角互补;65°
【解析】试题分析:根据对顶角相等求出∠1和∠2,根据平行线的性质求出∠4=∠2,2+∠3=180°,代入求出即可.
试题解析:∵∠1=∠2(对顶角相等),∠1+∠2=230°,
∴∠1=∠2=115°,
∵b∥c,
∴∠4=∠2=115°,(两直线平行,内错角相等),
∠2+∠3=180°,(两直线平行,同旁内角互补),
∴∠3=180° ∠2=65°,
故答案为:对顶角相等,115°,115°,两直线平行,内错角相等,两直线平行,同旁内角互补,65°.
17.证明见解析
【解析】试题分析:根据两直线平行,同位角相等,可得到∠1与∠3的关系,再根据对顶角相等可证明。
试题解析:∵a∥b
∴∠1=∠3(两直线平行,同位角相等)
又∵∠2=∠3(对顶角相等)
∴∠1=∠2.
18.∠BEF=∠EFC,理由详见解析.
【解析】试题解析:延长BE交直线CD于G,根据两直线平行,内错角相等可得∠1=∠3,从而得到∠2=∠3,再根据同位角相等,两直线平行可得BG∥CF,然后根据两直线平行,内错角相等可得∠BEF=∠EFC.
试题解析:∠BEF=∠EFC.
理由如下:如图,延长BE交直线CD于G,
∵AB∥CD,
∴∠1=∠3,
∵∠1=∠2,
∴∠2=∠3,
∴BG∥CF,
∴∠BEF=∠EFC.
19.见解析
【解析】试题分析:先根据平行线的性质得出∠B+∠BCE=180°,∠B=∠BCD,再根据CM平分∠BCE可知∠1=∠2,再由CN⊥CM可知,∠2+∠3=90°,故∠1+∠4=90°,所以∠3=∠4,故可得出结论.
试题解析:∵AB∥DE,
∴∠B+∠BCE=180°,∠B=∠BCD,
∵CM平分∠BCE,
∴∠1=∠2,
∵CN⊥CM,
∴∠2+∠3=90°,∠1+∠4=90°,
∴∠3=∠4,
∵∠3+∠4=∠BCD,
∴∠B=2∠DCN.
20.见解析
【解析】试题分析:甲可以运用两直线平行,同旁内角互补进行分析得到 乙丙结合两直线平行,内错角相等进行分析,即可求解.
试题解析:
甲: 理由如下:
如图,过点P作PE∥AB,
∵AB∥CD,PE∥AB,
∴AB∥CD∥PE,
乙: 理由如下:
如图,过点P作PE∥AB,
∵AB∥CD,PE∥AB,
∴AB∥CD∥PE,
丙: 理由如下:
如图,过点P作PE∥AB,
∵AB∥CD,
∴PF∥CD,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.3 平行线的性质同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.平行线的性质1:两条平行直线被第三条直线所截,同位角相等.可简说成两直线平行,同位角相等.
2.平行线的性质2:两条平行直线被第三条直线所截,内错角相等.可简说成两直线平行,内错角相等.
3.平行线的性质3:两条平行直线被第三条直线所截,同旁内角互补.可简说成两直线平行,同旁内角互补 .
基础知识和能力拓展精练
一、选择题
1.如图,已知∠AOB=70°,OC平分∠AOB,DC∥OB,则∠C为( )
A. 20° B. 35° C. 45° D. 70°
2.如图, 下列各式中正确的是( )
A. B.
C. D.
3.如图,如果AB∥CD,那么图中相等的内错角是( )
A. ∠1与∠5,∠2与∠6; B. ∠3与∠7,∠4与∠8;
C. ∠5与∠1,∠4与∠8; D. ∠2与∠6,∠7与∠3
4.如图,AC∥DF,AB∥EF,若∠2=50°,则∠1的大小是( )
A. 60° B. 50° C. 40° D. 30°
5.如图,AB∥CD,EF交AB、CD于点E、F,EG平分∠BEF,交CD于点G.若∠1=40°,则∠EGF=( )
A. 20° B. 40° C. 70° D. 110°
6.如图,将三角板的直角顶点放在直尺的一边上,若,则的度数为( )
A. B. C. D.
7.如图所示,下列推理不正确的是( ).
A. 若,则 B. 若,则
C. 若,则 D. 若,则
8.如图,由AC∥ED,可知相等的角有( )
A. 6对 B. 5对 C. 4对 D. 3对
二、填空题
9.如图为某条公路的示意图,两次拐弯后和原来的方向相同,即拐弯前后的两条路互相平行,第一次拐的角为∠M=150°,则第二次拐的角∠N=_________.
10.如图,直线a∥b,直线a,b被直线c所截,∠1=37°,则∠2=________.
11.如图,a∥b,∠1=110°,∠3=40°,则∠2=_________°
12.如图,已知AD //BC,∠B=32,DB平分∠ADE,则∠DEC=________.
13.如图,四边形ABCD中,AD∥BC,∠A=110°,则∠B=_____.
14.如图,在A,B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42°,A,B两地同时开工,B地所挖水渠走向应为南偏东_______.
15.如图,已知,=____________
三、解答题
16.完成下面推理过程:
如图,∠1+∠2=230°,b∥c,则∠1,∠2,∠3,∠4各是多少度?
解:∵∠1=∠2(__________________),
∠1+∠2=230°,
∴∠1=∠2=___________(填度数).
∵b∥c,
∴∠4=∠2=_______(填度数)(_______________________________),
∠2+∠3=180°(________________________________),
∴∠3=180°-∠2=____________(填度数).
17.如图,直线,求证: .
18.如图,AB∥CD,∠1=∠2,∠BDF与 ∠EFC相等吗?为什么?
19.已知:如图,AB∥DE,CM平分∠BCE,CN⊥CM.求证:∠B=2∠DCN.
20.阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
参考答案
1.B
【解析】解:∵OC平分∠AOB,∴∠AOC=∠BOC=∠AOB=35°,∵CD∥OB,∴∠BOC=∠C=35°,故选B.
2.D
【解析】∵OP//QR//ST,∴∠2+∠PRQ=180°,∠3=∠SRQ=∠1+∠PRQ,
∴∠PRQ=180°-∠2,
∴∠3=∠1+180°-∠2,即∠2+∠3-∠1=180°.
故选D.
点睛:本题关键利用平行线的性质解题.
3.D
【解析】AB∥CD,所以∠2与∠6,∠7与∠3.故选D.
4.B
【解析】根据平行线的性质即可求解.
解:∵AC∥DF,
∴∠F=∠2=50°,
∵AB∥EF,
∴∠1=∠F=50°.
故选B.
5.C
【解析】∵∠1=40°,∴∠BEF=140°,
∵EG平分∠BEF,∴∠BEG=∠GEF=70°,
∵AB∥CD,∴∠BEG=∠EGF=70°.
故选C.
点睛:掌握平行线的性质以及角平分线的性质.
6.C
【解析】如图,因为AD∥BC,所以∠1=∠3=65°,因为∠2+∠3+90°=180°,所以∠2=90°-∠3=90°-65°=25°,故选C.
7.D
【解析】A. ∵∠1=∠C,∴AE ∥ CD( 同位角相等 , 两直线平行 ) ,故正确;
B. ∵∠2=∠BAE,∴AB ∥ DE( 内错角相等 , 两直线平行 ) ,故正确;
C. ∵∠B+∠BAD=180 ,∴AD ∥ BC( 同旁内角互补 , 两直线平行 ) ,故正确;
D. ∵∠C+∠ADC=180 ,∴AD ∥ BC( 同旁内角互补 , 两直线平行 ) ,故错误。
故选D.
8.B
【解析】试题解析:如图,
∵AC∥ED,
∴∠BED=∠BAC,∠FAC=∠FED,∠EDF=∠1,∠1=∠2,∠C=∠BDE.共5对.
故选B.
9.150°
【解析】∵AM∥BN,
∴∠AMN=∠BNM=150°.
故答案为150°.
10.143°
【解析】
∵a∥b,∴∠1=∠3=37°,∴∠2=180°-37°=143°.
故答案为143°.
11.70
【解析】试题解析:如图,
∵a∥b,∠3=40°,
∴∠4=∠3=40°.
∵∠1=∠2+∠4=110°,
∴∠2=110°-∠4=110°-40°=70°.
故答案为:70.
12.
【解析】∵AD //BC,
∴∠ADB=∠B=32°.
∵DB平分∠ADE,
∴∠ADB=∠EDB=∠B=32°,
∴∠ADE=32°+32°=64°,
∴∠DEC=∠ADE=64°.
13.70°
【解析】因为AD∥BC,所以∠A+∠B=180°,因为∠A=110°,所以∠B=70°,故答案为70°.
14.42°
【解析】试题解析:
因为两个北方向是平行的,即AC∥BD,
所以A点北偏西的角与B点南偏东的角是内错角,
因此它们都等于42°.
故答案为:42°.
15.
【解析】试题解析:如图,
过E点作EF∥AB,
∵AB∥CD
∴EF∥AB∥CD
∴∠ABE+∠FEB=180°
∠DCE=∠FEC
∵∠ABE=120°, ∠DCE=25°
∴∠BEF=60°∠FEC=25°
∴∠a=60°+25°=85°
16.对顶角相等;115°;115°;两直线平行,内错角相等;两直线平行,同旁内角互补;65°
【解析】试题分析:根据对顶角相等求出∠1和∠2,根据平行线的性质求出∠4=∠2,2+∠3=180°,代入求出即可.
试题解析:∵∠1=∠2(对顶角相等),∠1+∠2=230°,
∴∠1=∠2=115°,
∵b∥c,
∴∠4=∠2=115°,(两直线平行,内错角相等),
∠2+∠3=180°,(两直线平行,同旁内角互补),
∴∠3=180° ∠2=65°,
故答案为:对顶角相等,115°,115°,两直线平行,内错角相等,两直线平行,同旁内角互补,65°.
17.证明见解析
【解析】试题分析:根据两直线平行,同位角相等,可得到∠1与∠3的关系,再根据对顶角相等可证明。
试题解析:∵a∥b
∴∠1=∠3(两直线平行,同位角相等)
又∵∠2=∠3(对顶角相等)
∴∠1=∠2.
18.∠BEF=∠EFC,理由详见解析.
【解析】试题解析:延长BE交直线CD于G,根据两直线平行,内错角相等可得∠1=∠3,从而得到∠2=∠3,再根据同位角相等,两直线平行可得BG∥CF,然后根据两直线平行,内错角相等可得∠BEF=∠EFC.
试题解析:∠BEF=∠EFC.
理由如下:如图,延长BE交直线CD于G,
∵AB∥CD,
∴∠1=∠3,
∵∠1=∠2,
∴∠2=∠3,
∴BG∥CF,
∴∠BEF=∠EFC.
19.见解析
【解析】试题分析:先根据平行线的性质得出∠B+∠BCE=180°,∠B=∠BCD,再根据CM平分∠BCE可知∠1=∠2,再由CN⊥CM可知,∠2+∠3=90°,故∠1+∠4=90°,所以∠3=∠4,故可得出结论.
试题解析:∵AB∥DE,
∴∠B+∠BCE=180°,∠B=∠BCD,
∵CM平分∠BCE,
∴∠1=∠2,
∵CN⊥CM,
∴∠2+∠3=90°,∠1+∠4=90°,
∴∠3=∠4,
∵∠3+∠4=∠BCD,
∴∠B=2∠DCN.
20.见解析
【解析】试题分析:甲可以运用两直线平行,同旁内角互补进行分析得到 乙丙结合两直线平行,内错角相等进行分析,即可求解.
试题解析:
甲: 理由如下:
如图,过点P作PE∥AB,
∵AB∥CD,PE∥AB,
∴AB∥CD∥PE,
乙: 理由如下:
如图,过点P作PE∥AB,
∵AB∥CD,PE∥AB,
∴AB∥CD∥PE,
丙: 理由如下:
如图,过点P作PE∥AB,
∵AB∥CD,
∴PF∥CD,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
