人教A版高中数学必修五2.5.1《等比数列》获奖课件(46张)
文档属性
| 名称 | 人教A版高中数学必修五2.5.1《等比数列》获奖课件(46张) |  | |
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-02 10:37:41 | ||
图片预览











文档简介
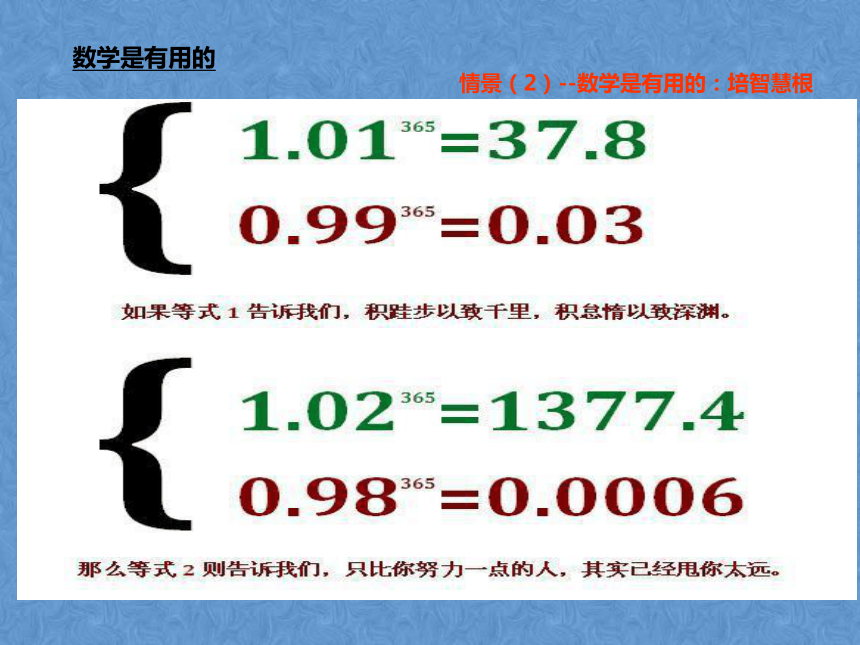
课件46张PPT。中国梦·全国优秀多媒体教学课件评选大赛课件等比数列数学是有用的---陈省身语 数学是有用的 古埃及国王拉阿乌斯有位能干的文书阿默斯.他用象形文字写了一部《算书》,记录了公元前2000年—前1700年间数学研究的一些成果.其中有这样一题,题中画了一个阶梯,其各级注数为7,49,343,2401,16807.并在数旁依次画了人、猫、鼠、大麦和量器.原书上并无任何说明,遂成为数学史上的一个难解谜.2000多年中无人能解释.你能解释吗?情景(1)--懂圣贤语
数学是有用的曰:“一尺之棰,日取其半,万世不竭.”庄子意思:“一尺长的木棒,每日取其一半,永远也取不完” 。如果将“一尺之棰”视为一份,
则每日剩下的部分依次为:情景(1)--懂圣贤语 数学是有用的给你一张足够大的纸,假设其厚度为0.1毫米,那么当你把这张纸对折了51次的时候,所达到的厚度有多少?? 把一张纸折叠51次,得到的大约是地球与太阳之间的距离!情景(2)--培智慧根 数学是有用的指数爆炸情景(2)--数学是有用的:培智慧根 数学是有用的 一种计算机病毒,可以查找计算机中的地址簿,通过邮件进行传播.如果把病毒制造者发送病毒称为第一轮,邮件接收者发送病毒称为第二轮,依此类推.假设每一轮每一台计算机都感染20台计算机,那么在不重复的情况下,这种病毒感染的计算机数构成一个什么样的数列呢?情景(2)--培智慧根 数学是有用的指数爆炸 一个穷人到富人那里去借钱,原以为富人会不愿意,哪知富人一口应承了下来,但提出了如下条件:在30天中,每天借给穷人10万元.借钱第一天,穷人还1分钱;第二天,还2分钱,以后每天所还的钱数都是前一天的2倍,30天后,互不相欠。穷人听后觉得很划算,本想一口气定下来,但又想到富人平时是吝啬出了名的,怕上当受骗,所以很为难。情景(3)--固君子本 数学是有用的国际象棋起源于印度,关于国际象棋有这样一个传说,国王要奖励国际象棋的发明者,问他有什么要求,发明者说:“请在棋盘上的第一个格子上放1粒麦子,第二个格子上放2粒麦子,第三个格子上放4粒麦子,第四个格子上放8粒麦子,依次类推,直到第64个格子放满为止。” 国王慷慨地答应了他。你认为国王有能力满足上述要求吗?左图为国际象棋的棋盘,棋盘有8x8=64格 1 2 3 4 5 6 7 8情景(3)--固君子本1844,6744,0737,0955,1615 数学是有用的 1 2 3 4 5 6 7 8“复利”是我国现行定期储蓄中的一种支付利息的方式,即把前一期的利息和本金加在一起算作本金,再计算下一期的利息,也就是通常说的“利滚利”.(我国现行定期储蓄中的自动转存业务实际上就是按复利支付利息的)计算本利和的公式:
本利和=本金×(1+利率)存期.
现在银行存入10000元,年利率为1.98%,则按照复利列出5年内各年末得到的本利和分别是多少?
情景(4)--为民生计 数学是有用的“时间”“年初本金”“年末本利和”三个量之间的对应关系,
各年末本利和(单位:元)组成了下面数列:
10 000×1.019 8,10 000×1.019 82,
10 000×1.019 83,10 000×1.019 84,
10 000×1.019 85. 情景(4)--为民生计 数学是有用的复习回顾一 一般地,如果一个数列从第2项起,每一项与前一项的差等于同一个常数,那么这个数列叫做等差数列。这个常数叫做等差数列的公差,用d表示。比较下列数列共同特点?(1) (2) (3)9,92,93,94,95,96, 9736,36×0.9,36×0.92, 36×0.93,…(4) 从第2项起,每一项与前
一项的比都等于同一常数.类比仿写一 一般地,如果一个数列从第2项起,每一项与前一项的差等于同一个常数,那么这个数列叫做等差数列。这个常数叫做等差数列的公差,用d表示。1、文字语言:一般,如果一个数列从第2项起,每一项与它前一项的比等于同一个常数,这个数列就叫做等比数列。这个常数叫做等比数列的公比,公比通常用字母q表示。(q≠0)2、数学符号语言:(递推公式)等比数列的每一项都不为0,即an≠0。等比数列定义如果一个数列从第2项起,每一项与前一项的差都等于同一个常数,那么这个数列叫做等差数列.这个常数叫做等差数列的公差,用d表示如果一个数列从第2项起,每一项与它前一项的比都等于同一个非0常数,那么这个数列叫做等比数列. 这个常数叫做等比数列的公比,用q表示.类比归纳概念内涵与外延一1. 公比是等比数列,从第2项起,
每一项与前一项的比,不能颠倒。2.对于一个给定的等比数列,它的
公比是同一个非零常数。3.等比数列的每一项都不为0,即an≠0。若an+1=anq(n∈N+,q为常数),则数列{an}是否是等比数列?反之能成立吗?概念内涵与外延二不一定是等比数列。这是因为:(1)若an=0,等式an+1=anq对n∈N恒成立,但从第二项起,每一项与它前一项的比就没有意义,故等比数列中任何一项都不能为零;(2)若q=0,等式an+1=anq,对n∈N仍恒成立,此时数列{an}从第二项起均为零,显然也不符合等比数列的定义,故等比数列中的公比q不能为零。
所以,如果an+1=anq(n∈N,q为常数),数列{an}不一定是等比数列。反之能成立。答:等比数列中(1)公比q为什么不能等于0?首项能等于0吗?(2)公比q=1时是什么数列?(3)q>1数列递增吗?q<1数列递减吗?概念内涵与外延三(1)公比q为什么不能等于0?首项能等于0吗?(2)公比q=1时是什么数列?(3)q>1数列递增吗?q<1数列递减吗?说明:(1)公比q≠0,则an≠0(n∈N);(2)既是等差又是等比数列为非零常数列;(3)q=1,常数列;既是等差又是等比数列。q<0,摆动数列;概念内涵与外延四 如果等比数列 {an}的首项是a1 ,公比是q,那么这个等比数列的第n项an如何表示? 概念内涵与外延四当n=1时,(等比数列通项公式)……∵∴……法一:(不完全归纳法)证明:将等式左右两边分别相乘可得:化简得:即:
此式对n=1也成立∵……∴法二:(叠乘法)想一想? 一般形式:1、判别下列数列是否为等比数列?
(2)1.2, 2.4 , -4.8 , -9.6 ……
(3)2, 2, 2, 2, …
(4)1, 0, 1, 0 …………课堂练习等差中项
若a,A,b三个数成等差数列,则A叫做a,b的等差中项。
2A=a+b
复习回顾二 如果在a与b中间插入一个数G,使a,G,b组成一个等比数列,则中间的数G叫做a与b的等比中项。若G2=ab,则a,G,b一定成等比数列吗?2、等比中项:类比仿写二 观察如下的两个数之间,插入一个什么数后,三个数就会成为一个等比数列:(1)1, , 9 (2)-1, ,-4
(3)-12, ,-3 (4)1, ,1±3±2±6±1概念巩固例1、在等比数列{an}中,已知: 求an.
例题剖析解得 因此,例1、在等比数列{an}中,已知: 解:设等比数列{an}的公比为q,由题意得求an.
规范解答求下列等比数列的第4,5项:(2)1.2,2.4,4.8,… (1) 5,-15,45,…课堂练习求下列等比数列的第4,5项:(2)1.2,2.4,4.8,… (1) 5,-15,45,…规范解答从1976年至1999年在我国累计推广种植杂交水稻35亿多亩,增产稻谷3500亿公斤。年增稻谷可养活6000万人口。 西方世界称他的杂交稻是“东方魔稻” ,并认为是解决下个世纪世界性饥饿问题的法宝。例2、袁隆平在培育某水稻新品种时,培育出第一代120粒种子,并且从第一代起,由以后各代的每一粒种子都可以得到下一代的120粒种子,到第5代时大约可以得到这个新品种的种子多少粒(保留两位有效数字)?例题剖析例2、 袁隆平在培育某水稻新品种时,培育出第一代120粒种子,并且从第一代起,由以后各代的每一粒种子都可以得到下一代的120粒种子,到第5代时大约可以得到这个新品种的种子多少粒(保留两位有效数字)?由于每代的种子数是它的前一代种子数的120倍,因此,逐代的种子数组成等比数列,记为 答:到第5代大约可以得到这种新品种的种子2.5×1010粒.解:规范解答例3 已知{an}、{bn}是项数相同的等比数列,试证{anbn}是等比数列. an+1-an=dd 叫公差q叫公比 an+1=an+d an+1=an q an= a1+(n-1)d an=a1qn-1 an=am+(n-m)d an=amqn-m课堂小结1、等比数列的定义;3、等比数列的通项公式及其简单应用:4、类比迁移思想的运用;2、仿写手法在概念定义中的运用;课后作业一变形1:已知{an}、{bn}为等比数列,c是非零常数,则{can}、{an+c}、{an+bn}是否为等比数列?变形3:已知{an} 为等比数列,问a10,a20,a30,…是否为等比数列?变形2:已知{an} 为等比数列,问a2,a4,a6,…是否为等比数列?课后作业二课后作业三(思考题)祝同学们自今日起,学业成正等比数列指数爆炸式递增!
前途焦虑压力成负等比数列指数爆炸式递减!
数学是有用的曰:“一尺之棰,日取其半,万世不竭.”庄子意思:“一尺长的木棒,每日取其一半,永远也取不完” 。如果将“一尺之棰”视为一份,
则每日剩下的部分依次为:情景(1)--懂圣贤语 数学是有用的给你一张足够大的纸,假设其厚度为0.1毫米,那么当你把这张纸对折了51次的时候,所达到的厚度有多少?? 把一张纸折叠51次,得到的大约是地球与太阳之间的距离!情景(2)--培智慧根 数学是有用的指数爆炸情景(2)--数学是有用的:培智慧根 数学是有用的 一种计算机病毒,可以查找计算机中的地址簿,通过邮件进行传播.如果把病毒制造者发送病毒称为第一轮,邮件接收者发送病毒称为第二轮,依此类推.假设每一轮每一台计算机都感染20台计算机,那么在不重复的情况下,这种病毒感染的计算机数构成一个什么样的数列呢?情景(2)--培智慧根 数学是有用的指数爆炸 一个穷人到富人那里去借钱,原以为富人会不愿意,哪知富人一口应承了下来,但提出了如下条件:在30天中,每天借给穷人10万元.借钱第一天,穷人还1分钱;第二天,还2分钱,以后每天所还的钱数都是前一天的2倍,30天后,互不相欠。穷人听后觉得很划算,本想一口气定下来,但又想到富人平时是吝啬出了名的,怕上当受骗,所以很为难。情景(3)--固君子本 数学是有用的国际象棋起源于印度,关于国际象棋有这样一个传说,国王要奖励国际象棋的发明者,问他有什么要求,发明者说:“请在棋盘上的第一个格子上放1粒麦子,第二个格子上放2粒麦子,第三个格子上放4粒麦子,第四个格子上放8粒麦子,依次类推,直到第64个格子放满为止。” 国王慷慨地答应了他。你认为国王有能力满足上述要求吗?左图为国际象棋的棋盘,棋盘有8x8=64格 1 2 3 4 5 6 7 8情景(3)--固君子本1844,6744,0737,0955,1615 数学是有用的 1 2 3 4 5 6 7 8“复利”是我国现行定期储蓄中的一种支付利息的方式,即把前一期的利息和本金加在一起算作本金,再计算下一期的利息,也就是通常说的“利滚利”.(我国现行定期储蓄中的自动转存业务实际上就是按复利支付利息的)计算本利和的公式:
本利和=本金×(1+利率)存期.
现在银行存入10000元,年利率为1.98%,则按照复利列出5年内各年末得到的本利和分别是多少?
情景(4)--为民生计 数学是有用的“时间”“年初本金”“年末本利和”三个量之间的对应关系,
各年末本利和(单位:元)组成了下面数列:
10 000×1.019 8,10 000×1.019 82,
10 000×1.019 83,10 000×1.019 84,
10 000×1.019 85. 情景(4)--为民生计 数学是有用的复习回顾一 一般地,如果一个数列从第2项起,每一项与前一项的差等于同一个常数,那么这个数列叫做等差数列。这个常数叫做等差数列的公差,用d表示。比较下列数列共同特点?(1) (2) (3)9,92,93,94,95,96, 9736,36×0.9,36×0.92, 36×0.93,…(4) 从第2项起,每一项与前
一项的比都等于同一常数.类比仿写一 一般地,如果一个数列从第2项起,每一项与前一项的差等于同一个常数,那么这个数列叫做等差数列。这个常数叫做等差数列的公差,用d表示。1、文字语言:一般,如果一个数列从第2项起,每一项与它前一项的比等于同一个常数,这个数列就叫做等比数列。这个常数叫做等比数列的公比,公比通常用字母q表示。(q≠0)2、数学符号语言:(递推公式)等比数列的每一项都不为0,即an≠0。等比数列定义如果一个数列从第2项起,每一项与前一项的差都等于同一个常数,那么这个数列叫做等差数列.这个常数叫做等差数列的公差,用d表示如果一个数列从第2项起,每一项与它前一项的比都等于同一个非0常数,那么这个数列叫做等比数列. 这个常数叫做等比数列的公比,用q表示.类比归纳概念内涵与外延一1. 公比是等比数列,从第2项起,
每一项与前一项的比,不能颠倒。2.对于一个给定的等比数列,它的
公比是同一个非零常数。3.等比数列的每一项都不为0,即an≠0。若an+1=anq(n∈N+,q为常数),则数列{an}是否是等比数列?反之能成立吗?概念内涵与外延二不一定是等比数列。这是因为:(1)若an=0,等式an+1=anq对n∈N恒成立,但从第二项起,每一项与它前一项的比就没有意义,故等比数列中任何一项都不能为零;(2)若q=0,等式an+1=anq,对n∈N仍恒成立,此时数列{an}从第二项起均为零,显然也不符合等比数列的定义,故等比数列中的公比q不能为零。
所以,如果an+1=anq(n∈N,q为常数),数列{an}不一定是等比数列。反之能成立。答:等比数列中(1)公比q为什么不能等于0?首项能等于0吗?(2)公比q=1时是什么数列?(3)q>1数列递增吗?q<1数列递减吗?概念内涵与外延三(1)公比q为什么不能等于0?首项能等于0吗?(2)公比q=1时是什么数列?(3)q>1数列递增吗?q<1数列递减吗?说明:(1)公比q≠0,则an≠0(n∈N);(2)既是等差又是等比数列为非零常数列;(3)q=1,常数列;既是等差又是等比数列。q<0,摆动数列;概念内涵与外延四 如果等比数列 {an}的首项是a1 ,公比是q,那么这个等比数列的第n项an如何表示? 概念内涵与外延四当n=1时,(等比数列通项公式)……∵∴……法一:(不完全归纳法)证明:将等式左右两边分别相乘可得:化简得:即:
此式对n=1也成立∵……∴法二:(叠乘法)想一想? 一般形式:1、判别下列数列是否为等比数列?
(2)1.2, 2.4 , -4.8 , -9.6 ……
(3)2, 2, 2, 2, …
(4)1, 0, 1, 0 …………课堂练习等差中项
若a,A,b三个数成等差数列,则A叫做a,b的等差中项。
2A=a+b
复习回顾二 如果在a与b中间插入一个数G,使a,G,b组成一个等比数列,则中间的数G叫做a与b的等比中项。若G2=ab,则a,G,b一定成等比数列吗?2、等比中项:类比仿写二 观察如下的两个数之间,插入一个什么数后,三个数就会成为一个等比数列:(1)1, , 9 (2)-1, ,-4
(3)-12, ,-3 (4)1, ,1±3±2±6±1概念巩固例1、在等比数列{an}中,已知: 求an.
例题剖析解得 因此,例1、在等比数列{an}中,已知: 解:设等比数列{an}的公比为q,由题意得求an.
规范解答求下列等比数列的第4,5项:(2)1.2,2.4,4.8,… (1) 5,-15,45,…课堂练习求下列等比数列的第4,5项:(2)1.2,2.4,4.8,… (1) 5,-15,45,…规范解答从1976年至1999年在我国累计推广种植杂交水稻35亿多亩,增产稻谷3500亿公斤。年增稻谷可养活6000万人口。 西方世界称他的杂交稻是“东方魔稻” ,并认为是解决下个世纪世界性饥饿问题的法宝。例2、袁隆平在培育某水稻新品种时,培育出第一代120粒种子,并且从第一代起,由以后各代的每一粒种子都可以得到下一代的120粒种子,到第5代时大约可以得到这个新品种的种子多少粒(保留两位有效数字)?例题剖析例2、 袁隆平在培育某水稻新品种时,培育出第一代120粒种子,并且从第一代起,由以后各代的每一粒种子都可以得到下一代的120粒种子,到第5代时大约可以得到这个新品种的种子多少粒(保留两位有效数字)?由于每代的种子数是它的前一代种子数的120倍,因此,逐代的种子数组成等比数列,记为 答:到第5代大约可以得到这种新品种的种子2.5×1010粒.解:规范解答例3 已知{an}、{bn}是项数相同的等比数列,试证{anbn}是等比数列. an+1-an=dd 叫公差q叫公比 an+1=an+d an+1=an q an= a1+(n-1)d an=a1qn-1 an=am+(n-m)d an=amqn-m课堂小结1、等比数列的定义;3、等比数列的通项公式及其简单应用:4、类比迁移思想的运用;2、仿写手法在概念定义中的运用;课后作业一变形1:已知{an}、{bn}为等比数列,c是非零常数,则{can}、{an+c}、{an+bn}是否为等比数列?变形3:已知{an} 为等比数列,问a10,a20,a30,…是否为等比数列?变形2:已知{an} 为等比数列,问a2,a4,a6,…是否为等比数列?课后作业二课后作业三(思考题)祝同学们自今日起,学业成正等比数列指数爆炸式递增!
前途焦虑压力成负等比数列指数爆炸式递减!
