第七章 相交线与平行线单元检测试题(A卷含解析)
文档属性
| 名称 | 第七章 相交线与平行线单元检测试题(A卷含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-02 16:12:54 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
六年级下册第七章相交线与平行线单元检测
(时间60分钟,分数100分)
一、选择题(共10个小题,每小题3分,共30分)
1.如图,直线AB,CD被直线EF所截,则∠3的同旁内角是( )
A.∠1 B.∠2 C.∠4 D.∠5
2.如图,点C在∠AOB的边OB上,用尺规作出了CN∥OA,作图痕迹中,弧FG是( )
A.以点C为圆心,OD为半径的弧 B.以点C为圆心,DM为半径的弧
C.以点E为圆心,OD为半径的弧 D.以点E为圆心,DM为半径的弧
3.点P为直线l外一点,点A,B,C为直线l上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线l的距离为( )21世纪教育网版权所有
A.4cm B.2 cm C.小于2cm D.不大于2 cm
4.如图,若∠1=70°,∠2=110°,∠3=70°,则有( )
A.a∥b B.c∥d C.a⊥d D.任意两条都无法判定是否平行
5.如图,下列条件:①∠1=∠3;②∠2=∠3;③∠4=∠5;④∠2+
∠4=180°,其中能判断直线l1∥l2的有( )
(A)1个 (B)2个 (C)3个 (D)4个
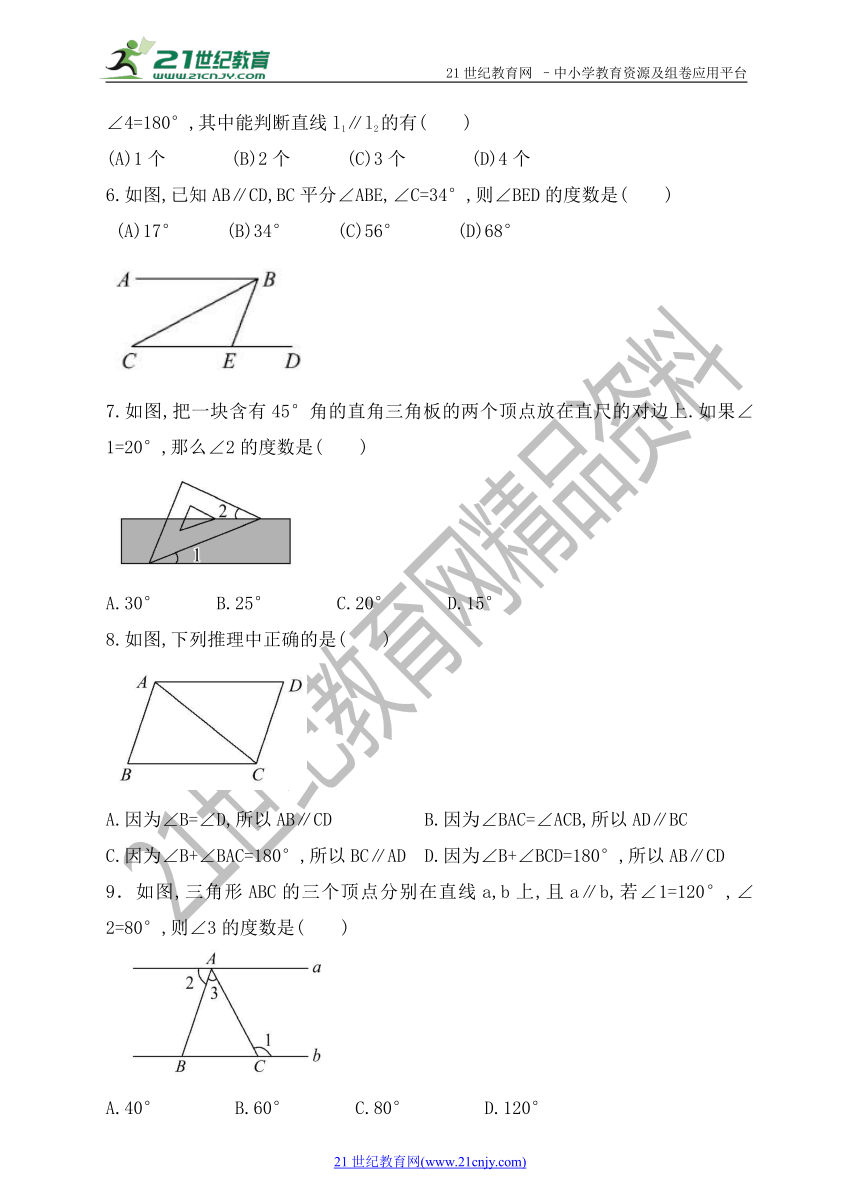
6.如图,已知AB∥CD,BC平分∠ABE,∠C=34°,则∠BED的度数是( )
(A)17° (B)34° (C)56° (D)68°
7.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )21·世纪*教育网
A.30° B.25° C.20° D.15°
8.如图,下列推理中正确的是( )
A.因为∠B=∠D,所以AB∥CD B.因为∠BAC=∠ACB,所以AD∥BC
C.因为∠B+∠BAC=180°,所以BC∥AD D.因为∠B+∠BCD=180°,所以AB∥CD
9.如图,三角形ABC的三个顶点分别在直线a,b上,且a∥b,若∠1=120°,∠2=80°,则∠3的度数是( )21cnjy.com
A.40° B.60° C.80° D.120°
10.一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向平行行驶,那么这两个拐弯的角度可能是( )
A.先向左转130°,再向左转50° B.先向左转50°,再向右转50°
C.先向左转50°,再向右转40° D.先向左转50°,再向左转40°
二、(共8个小题,每小题4分,共32分)
11.尺规作图的画图工具是 .
12.如图,直尺一边AB与量角器的零刻度线CD平行,若量角器的一条刻度线OF的读数为70°,OF与AB交于点E,那么∠AEF= 度.21*cnjy*com
13.如图,OA⊥OC于O,直线BD过点O,∠AOB=40°,则∠COD等于________.
14.如图所示,用直尺和三角尺作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为________.21教育网
15.如图所示,图中的同位角有_______对.
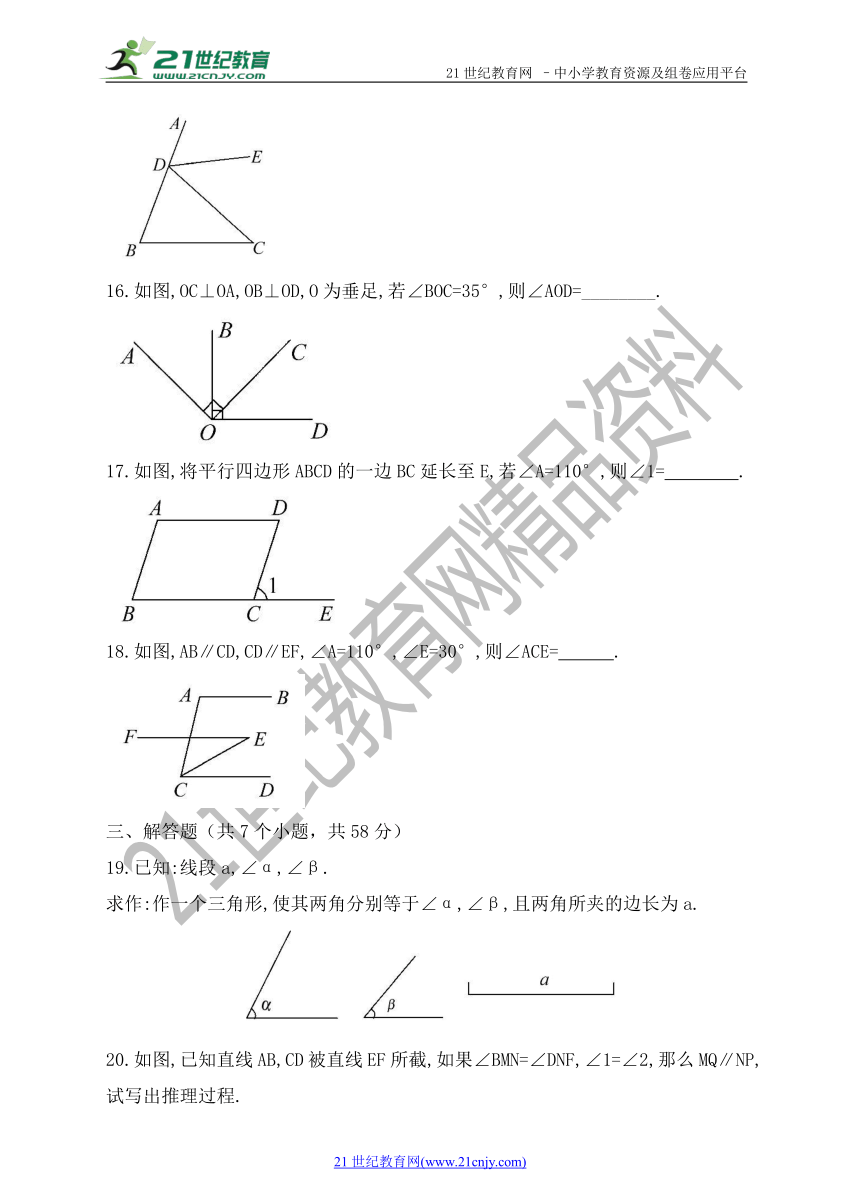
16.如图,OC⊥OA,OB⊥OD,O为垂足,若∠BOC=35°,则∠AOD=________.
17.如图,将平行四边形ABCD的一边BC延长至E,若∠A=110°,则∠1= .
18.如图,AB∥CD,CD∥EF,∠A=110°,∠E=30°,则∠ACE= .
三、解答题(共7个小题,共58分)
19.已知:线段a,∠α,∠β.
求作:作一个三角形,使其两角分别等于∠α,∠β,且两角所夹的边长为a.
20.如图,已知直线AB,CD被直线EF所截,如果∠BMN=∠DNF,∠1=∠2,那么MQ∥NP,试写出推理过程.【来源:21cnj*y.co*m】
21.一辆汽车在直线形的公路上由A向B行驶,M,N分别是位于公路AB两侧的学校,如图所示.
(1)汽车在公路上行驶时,会对两个学校的教学都造成影响,当汽车行驶到何处时,分别对两个学校的影响最大 在图上标出来.【出处:21教育名师】
(2)当汽车从A向B行驶时,在哪一段上对两个学校的影响越来越大 哪一段上对M学校的影响逐渐减小,而对N学校的影响逐渐增大 【版权所有:21教育】
22.如图,∠BAF=46°,∠ACE=136°,CE⊥CD,问CD∥AB吗 为什么
23.如图,点P是线段AB的中点,经过点P画BC的平行线交AC于点Q,再经过点Q画AB的平行线,交BC于点S.2·1·c·n·j·y
(1)用刻度尺度量后确定AQ与QC,CS与BS的长度关系.
(2)用刻度尺度量后确定PQ与BC,QS与AB的长度关系,你发现了什么 用简洁的语言把你发现的规律叙述出来.
24.如图,∠B,∠D的两边分别平行.
在图①中,∠B与∠D的数量关系为 .
在图②中,∠B与∠D的数量关系为 .
试分别说明理由,并用一句话归纳结论.
25.如图,已知AB∥CD,分别探究下面四个图形中∠APC和∠PAB,∠PCD的关系,请从你所得四个关系中选出任意一个,说明你探究的结论的正确性.
结论:(1) . (2) .
(3) .
(4) .
选择结论: ,说明理由.
参考答案:
一、选择题(共10个小题,每小题3分,共30分)
1.如图,直线AB,CD被直线EF所截,则∠3的同旁内角是( )
(A)∠1 (B)∠2 (C)∠4 (D)∠5
【解析】选B.∠3的同旁内角为∠2.
2.如图,点C在∠AOB的边OB上,用尺规作出了CN∥OA,作图痕迹中,弧FG是( )
(A)以点C为圆心,OD为半径的弧 (B)以点C为圆心,DM为半径的弧
(C)以点E为圆心,OD为半径的弧 (D)以点E为圆心,DM为半径的弧
【解析】选D.根据尺规作图中作一个角等于已知角的作图方法,可知D正确.
3.点P为直线l外一点,点A,B,C为直线l上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线l的距离为( )www.21-cn-jy.com
(A)4 cm (B)2 cm (C)小于2 cm (D)不大于2 cm
【解析】选D.由题意知,PC4.如图,若∠1=70°,∠2=110°,∠3=70°,则有( )
A.a∥b B.c∥d C.a⊥d D.任意两条都无法判定是否平行
【解析】选A.如图,由∠2=110°,可得∠2的邻补角∠4等于70°,而∠1=70°,所以∠1=∠4,又因为∠1与∠4是同位角,所以a∥b.21教育名师原创作品
5.如图,下列条件:①∠1=∠3;②∠2=∠3;③∠4=∠5;④∠2+
∠4=180°,其中能判断直线l1∥l2的有( )
(A)1个 (B)2个 (C)3个 (D)4个
【解析】选C.由“内错角相等,两直线平行”得①可以;由“同位角相等,两直线平行”得③可以;由“同旁内角互补,两直线平行”得④可以.
6.如图,已知AB∥CD,BC平分∠ABE,∠C=34°,则∠BED的度数是( )
(A)17° (B)34°(C)56° (D)68°
【解析】选D.因为AB∥CD,所以∠ABC=∠C=34°,
又因为BC平分∠ABE,所以∠ABE=2∠ABC=68°,
所以∠BED=∠ABE=68°.
7.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
(A)30° (B)25° (C)20° (D)15°
【解析】选B.因为a∥b,∠1=20°,
所以∠3=∠1=20°,
所以∠2=45°-20°=25°.
8.如图,下列推理中正确的是( )
A.因为∠B=∠D,所以AB∥CD B.因为∠BAC=∠ACB,所以AD∥BC
C.因为∠B+∠BAC=180°,所以BC∥AD D.因为∠B+∠BCD=180°,所以AB∥CD
【解析】选D.由图得∠B与∠BCD是AB,CD被直线BC所截得到的同旁内角,所以由“同旁内角互补,两直线平行”得D正确.
9.如图,三角形ABC的三个顶点分别在直线a,b上,且a∥b,若∠1=120°,∠2=80°,则∠3的度数是( )
A.40° B.60° C.80° D.120°
【解析】选A.因为a∥b,所以∠1=∠2+∠3=120°,
又因为∠2=80°,所以∠3=120°-∠2=120°-80°=40°.
10.一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向平行行驶,那么这两个拐弯的角度可能是( )
(A)先向左转130°,再向左转50°
(B)先向左转50°,再向右转50°
(C)先向左转50°,再向右转40°
(D)先向左转50°,再向左转40°
【解析】选B.先向左转a°,再向右转b°形成的两个角是同位角关系,因为两次拐弯后,仍在原来的方向平行行驶,即两直线平行,所以a°=b°,故选B.
二、(共8个小题,每小题4分,共32分)
11.尺规作图的画图工具是 .
【解析】尺规作图的画图工具是没有刻度的直尺和圆规.
答案:没有刻度的直尺和圆规
12.如图,直尺一边AB与量角器的零刻度线CD平行,若量角器的一条刻度线OF的读数为70°,OF与AB交于点E,那么∠AEF= 度.www-2-1-cnjy-com
【解析】直尺的对边互相平行,∠COF与∠AEF是同位角,又∠COF=70°,根据两直线平行,同位角相等,得∠AEF=70°.
答案:70
13.如图,OA⊥OC于O,直线BD过点O,∠AOB=40°,则∠COD等于________.
【解析】因为OA⊥OC,所以∠AOC=90°,因为∠AOB=40°,所以∠BOC=50°,所以∠COD=130°.
答案:130°
14.如图所示,用直尺和三角尺作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为________.
【解析】三角尺在平移的过程中,角度没有发生变化,根据同位角相等,两直线平行就能判定直线AB与直线CD的位置关系为平行.2-1-c-n-j-y
答案:平行
15.如图所示,图中的同位角有_______对.
【解析】图中的同位角是∠ADE与∠B,∠ADC与∠B,共2对.
答案:2
16.如图,OC⊥OA,OB⊥OD,O为垂足,若∠BOC=35°,则∠AOD=________.
【解析】因为OC⊥OA,OB⊥OD,
所以∠AOB+∠BOC=90°,∠COD+∠BOC=90°,
所以∠AOB+2∠BOC+∠COD=180°,
即∠AOD+∠BOC=180°,
因为∠BOC=35°,所以∠AOD=145°.
答案:145°
17.如图,将平行四边形ABCD的一边BC延长至E,若∠A=110°,则∠1= .
【解析】因为平行四边形对边平行,所以AD∥BC,AB∥CD.又因为∠A=110°,根据平行线的特征:两直线平行,同旁内角互补,同位角相等,所以∠1=∠B=
180°-∠A=70°.
答案:70°
18.如图,AB∥CD,CD∥EF,∠A=110°,∠E=30°,则∠ACE= .
【解析】因为AB∥CD,∠A=110°,
所以∠ACD=180°-∠A=180°-110°=70°,
因为CD∥EF,∠E=30°,所以∠ECD=∠E=30°,
所以∠ACE=∠ACD-∠ECD=70°-30°=40°.
答案:40°
三、解答题(共7个小题,共58分)
19.已知:线段a,∠α,∠β.
求作:作一个三角形,使其两角分别等于∠α,∠β,且两角所夹的边长为a.
【解析】作法:①作线段AB=a;②过点A作∠CAB=∠α,过点B作∠CBA=∠β,两边交于点C.则△ABC就是要求作的图形.
20.如图,已知直线AB,CD被直线EF所截,如果∠BMN=∠DNF,∠1=∠2,那么MQ∥NP,试写出推理过程.
【解析】因为∠BMN=∠DNF,∠1=∠2,所以∠BMN+∠1=∠DNF+∠2,即∠QMN=
∠PNF,则MQ∥NP.
21.一辆汽车在直线形的公路上由A向B行驶,M,N分别是位于公路AB两侧的学校,如图所示.
(1)汽车在公路上行驶时,会对两个学校的教学都造成影响,当汽车行驶到何处时,分别对两个学校的影响最大 在图上标出来.
(2)当汽车从A向B行驶时,在哪一段上对两个学校的影响越来越大 哪一段上对M学校的影响逐渐减小,而对N学校的影响逐渐增大
【解析】(1)如图,作MC⊥AB于点C,ND⊥AB于点D,根据垂线段最短,所以在点C处对M学校的影响最大,在点D处对N学校的影响最大.
(2)由点A向点C行驶时,对两个学校的影响逐渐增大;由点C向点D行驶时,对M学校的影响逐渐减小,对N学校的影响逐渐增大.
22.如图,∠BAF=46°,∠ACE=136°,CE⊥CD,问CD∥AB吗 为什么
【解析】CD∥AB.
理由:因为∠BAF+∠BAC=180°(邻补角),
∠BAF=46°(已知),
所以∠BAC=180°-∠BAF=180°-46°=134°.
因为CE⊥CD(已知),
所以∠DCE=90°(垂直的性质),
又因为∠FCD+∠DCE+∠ACE=360°,
所以∠FCD=360°-∠DCE-∠ACE
=360°-90°-136°=134°,
所以∠BAC=∠FCD(等量代换),
所以CD∥AB(内错角相等,两直线平行).
23.如图,点P是线段AB的中点,经过点P画BC的平行线交AC于点Q,再经过点Q画AB的平行线,交BC于点S.
(1)用刻度尺度量后确定AQ与QC,CS与BS的长度关系.
(2)用刻度尺度量后确定PQ与BC,QS与AB的长度关系,你发现了什么 用简洁的语言把你发现的规律叙述出来.
【解析】所画的平行线如图所示:
(1)经度量得到AQ=QC,CS=BS.
(2)经度量得到PQ=BC,QS=AB.
经过三角形一边的中点,画另一边的平行线,则这条平行线平分第三边,三角形两边中点之间线段的长度等于第三边长度的一半21*cnjy*com
24.如图,∠B,∠D的两边分别平行.
在图①中,∠B与∠D的数量关系为 .
在图②中,∠B与∠D的数量关系为 .
试分别说明理由,并用一句话归纳结论.
【解析】图①中∠B与∠D相等.理由:
如图(1),因为BE∥DF,所以∠CME=∠D,
因为AB∥DC,所以∠B=∠CME,所以∠B=∠D.
图②中∠B与∠D互补.理由:
如图(2),因为BE∥DF,所以∠BND+∠D=180°,
因为AB∥DC,所以∠B=∠BND,
所以∠B+∠D=180°.
结论:如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补.
25.如图,已知AB∥CD,分别探究下面四个图形中∠APC和∠PAB,∠PCD的关系,请从你所得四个关系中选出任意一个,说明你探究的结论的正确性.
结论:(1) . (2) .
(3) .
(4) .
选择结论: ,说明理由.
【解析】结论:(1)∠PAB+∠APC+∠PCD=360°
(2)∠APC =∠PAB+∠PCD
(3)∠APC =∠PCD-∠PAB
(4)∠APC =∠PAB-∠PCD
选择结论:答案不惟一,
理由:(1)如图(1),过点P作PQ∥AB,因为AB∥CD,所以PQ∥CD,由PQ∥AB可得
∠PAB+∠APQ=180°;由PQ∥CD得∠PCD+∠CPQ=180°,所以∠PAB+∠APQ+∠PCD+∠CPQ=360°,即∠PAB+∠APC+∠PCD=360°.21·cn·jy·com
(2)如图(2),过点P作PQ∥AB,因为AB∥CD,所以PQ∥CD,由PQ∥AB可得∠PAB=∠APQ;由PQ∥CD得∠PCD=∠CPQ,所以∠APC =∠PAB+∠PCD.【来源:21·世纪·教育·网】
(3)因为AB∥CD,所以∠PEB=∠PCD,又因为∠AEP+∠APC+∠PAB=180°,∠PEB+
∠AEP=180°,所以∠APC+∠PAB=∠PCD,
即∠APC =∠PCD-∠PAB.
(4)因为AB∥CD,所以∠PED=∠PAB,又因为∠CEP+∠APC+∠DCP=180°,∠PED+
∠CEP=180°,所以∠APC+∠PCD=∠PAB,
即∠APC =∠PAB-∠PCD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
六年级下册第七章相交线与平行线单元检测
(时间60分钟,分数100分)
一、选择题(共10个小题,每小题3分,共30分)
1.如图,直线AB,CD被直线EF所截,则∠3的同旁内角是( )
A.∠1 B.∠2 C.∠4 D.∠5
2.如图,点C在∠AOB的边OB上,用尺规作出了CN∥OA,作图痕迹中,弧FG是( )
A.以点C为圆心,OD为半径的弧 B.以点C为圆心,DM为半径的弧
C.以点E为圆心,OD为半径的弧 D.以点E为圆心,DM为半径的弧
3.点P为直线l外一点,点A,B,C为直线l上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线l的距离为( )21世纪教育网版权所有
A.4cm B.2 cm C.小于2cm D.不大于2 cm
4.如图,若∠1=70°,∠2=110°,∠3=70°,则有( )
A.a∥b B.c∥d C.a⊥d D.任意两条都无法判定是否平行
5.如图,下列条件:①∠1=∠3;②∠2=∠3;③∠4=∠5;④∠2+
∠4=180°,其中能判断直线l1∥l2的有( )
(A)1个 (B)2个 (C)3个 (D)4个
6.如图,已知AB∥CD,BC平分∠ABE,∠C=34°,则∠BED的度数是( )
(A)17° (B)34° (C)56° (D)68°
7.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )21·世纪*教育网
A.30° B.25° C.20° D.15°
8.如图,下列推理中正确的是( )
A.因为∠B=∠D,所以AB∥CD B.因为∠BAC=∠ACB,所以AD∥BC
C.因为∠B+∠BAC=180°,所以BC∥AD D.因为∠B+∠BCD=180°,所以AB∥CD
9.如图,三角形ABC的三个顶点分别在直线a,b上,且a∥b,若∠1=120°,∠2=80°,则∠3的度数是( )21cnjy.com
A.40° B.60° C.80° D.120°
10.一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向平行行驶,那么这两个拐弯的角度可能是( )
A.先向左转130°,再向左转50° B.先向左转50°,再向右转50°
C.先向左转50°,再向右转40° D.先向左转50°,再向左转40°
二、(共8个小题,每小题4分,共32分)
11.尺规作图的画图工具是 .
12.如图,直尺一边AB与量角器的零刻度线CD平行,若量角器的一条刻度线OF的读数为70°,OF与AB交于点E,那么∠AEF= 度.21*cnjy*com
13.如图,OA⊥OC于O,直线BD过点O,∠AOB=40°,则∠COD等于________.
14.如图所示,用直尺和三角尺作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为________.21教育网
15.如图所示,图中的同位角有_______对.
16.如图,OC⊥OA,OB⊥OD,O为垂足,若∠BOC=35°,则∠AOD=________.
17.如图,将平行四边形ABCD的一边BC延长至E,若∠A=110°,则∠1= .
18.如图,AB∥CD,CD∥EF,∠A=110°,∠E=30°,则∠ACE= .
三、解答题(共7个小题,共58分)
19.已知:线段a,∠α,∠β.
求作:作一个三角形,使其两角分别等于∠α,∠β,且两角所夹的边长为a.
20.如图,已知直线AB,CD被直线EF所截,如果∠BMN=∠DNF,∠1=∠2,那么MQ∥NP,试写出推理过程.【来源:21cnj*y.co*m】
21.一辆汽车在直线形的公路上由A向B行驶,M,N分别是位于公路AB两侧的学校,如图所示.
(1)汽车在公路上行驶时,会对两个学校的教学都造成影响,当汽车行驶到何处时,分别对两个学校的影响最大 在图上标出来.【出处:21教育名师】
(2)当汽车从A向B行驶时,在哪一段上对两个学校的影响越来越大 哪一段上对M学校的影响逐渐减小,而对N学校的影响逐渐增大 【版权所有:21教育】
22.如图,∠BAF=46°,∠ACE=136°,CE⊥CD,问CD∥AB吗 为什么
23.如图,点P是线段AB的中点,经过点P画BC的平行线交AC于点Q,再经过点Q画AB的平行线,交BC于点S.2·1·c·n·j·y
(1)用刻度尺度量后确定AQ与QC,CS与BS的长度关系.
(2)用刻度尺度量后确定PQ与BC,QS与AB的长度关系,你发现了什么 用简洁的语言把你发现的规律叙述出来.
24.如图,∠B,∠D的两边分别平行.
在图①中,∠B与∠D的数量关系为 .
在图②中,∠B与∠D的数量关系为 .
试分别说明理由,并用一句话归纳结论.
25.如图,已知AB∥CD,分别探究下面四个图形中∠APC和∠PAB,∠PCD的关系,请从你所得四个关系中选出任意一个,说明你探究的结论的正确性.
结论:(1) . (2) .
(3) .
(4) .
选择结论: ,说明理由.
参考答案:
一、选择题(共10个小题,每小题3分,共30分)
1.如图,直线AB,CD被直线EF所截,则∠3的同旁内角是( )
(A)∠1 (B)∠2 (C)∠4 (D)∠5
【解析】选B.∠3的同旁内角为∠2.
2.如图,点C在∠AOB的边OB上,用尺规作出了CN∥OA,作图痕迹中,弧FG是( )
(A)以点C为圆心,OD为半径的弧 (B)以点C为圆心,DM为半径的弧
(C)以点E为圆心,OD为半径的弧 (D)以点E为圆心,DM为半径的弧
【解析】选D.根据尺规作图中作一个角等于已知角的作图方法,可知D正确.
3.点P为直线l外一点,点A,B,C为直线l上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线l的距离为( )www.21-cn-jy.com
(A)4 cm (B)2 cm (C)小于2 cm (D)不大于2 cm
【解析】选D.由题意知,PC
A.a∥b B.c∥d C.a⊥d D.任意两条都无法判定是否平行
【解析】选A.如图,由∠2=110°,可得∠2的邻补角∠4等于70°,而∠1=70°,所以∠1=∠4,又因为∠1与∠4是同位角,所以a∥b.21教育名师原创作品
5.如图,下列条件:①∠1=∠3;②∠2=∠3;③∠4=∠5;④∠2+
∠4=180°,其中能判断直线l1∥l2的有( )
(A)1个 (B)2个 (C)3个 (D)4个
【解析】选C.由“内错角相等,两直线平行”得①可以;由“同位角相等,两直线平行”得③可以;由“同旁内角互补,两直线平行”得④可以.
6.如图,已知AB∥CD,BC平分∠ABE,∠C=34°,则∠BED的度数是( )
(A)17° (B)34°(C)56° (D)68°
【解析】选D.因为AB∥CD,所以∠ABC=∠C=34°,
又因为BC平分∠ABE,所以∠ABE=2∠ABC=68°,
所以∠BED=∠ABE=68°.
7.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
(A)30° (B)25° (C)20° (D)15°
【解析】选B.因为a∥b,∠1=20°,
所以∠3=∠1=20°,
所以∠2=45°-20°=25°.
8.如图,下列推理中正确的是( )
A.因为∠B=∠D,所以AB∥CD B.因为∠BAC=∠ACB,所以AD∥BC
C.因为∠B+∠BAC=180°,所以BC∥AD D.因为∠B+∠BCD=180°,所以AB∥CD
【解析】选D.由图得∠B与∠BCD是AB,CD被直线BC所截得到的同旁内角,所以由“同旁内角互补,两直线平行”得D正确.
9.如图,三角形ABC的三个顶点分别在直线a,b上,且a∥b,若∠1=120°,∠2=80°,则∠3的度数是( )
A.40° B.60° C.80° D.120°
【解析】选A.因为a∥b,所以∠1=∠2+∠3=120°,
又因为∠2=80°,所以∠3=120°-∠2=120°-80°=40°.
10.一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向平行行驶,那么这两个拐弯的角度可能是( )
(A)先向左转130°,再向左转50°
(B)先向左转50°,再向右转50°
(C)先向左转50°,再向右转40°
(D)先向左转50°,再向左转40°
【解析】选B.先向左转a°,再向右转b°形成的两个角是同位角关系,因为两次拐弯后,仍在原来的方向平行行驶,即两直线平行,所以a°=b°,故选B.
二、(共8个小题,每小题4分,共32分)
11.尺规作图的画图工具是 .
【解析】尺规作图的画图工具是没有刻度的直尺和圆规.
答案:没有刻度的直尺和圆规
12.如图,直尺一边AB与量角器的零刻度线CD平行,若量角器的一条刻度线OF的读数为70°,OF与AB交于点E,那么∠AEF= 度.www-2-1-cnjy-com
【解析】直尺的对边互相平行,∠COF与∠AEF是同位角,又∠COF=70°,根据两直线平行,同位角相等,得∠AEF=70°.
答案:70
13.如图,OA⊥OC于O,直线BD过点O,∠AOB=40°,则∠COD等于________.
【解析】因为OA⊥OC,所以∠AOC=90°,因为∠AOB=40°,所以∠BOC=50°,所以∠COD=130°.
答案:130°
14.如图所示,用直尺和三角尺作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为________.
【解析】三角尺在平移的过程中,角度没有发生变化,根据同位角相等,两直线平行就能判定直线AB与直线CD的位置关系为平行.2-1-c-n-j-y
答案:平行
15.如图所示,图中的同位角有_______对.
【解析】图中的同位角是∠ADE与∠B,∠ADC与∠B,共2对.
答案:2
16.如图,OC⊥OA,OB⊥OD,O为垂足,若∠BOC=35°,则∠AOD=________.
【解析】因为OC⊥OA,OB⊥OD,
所以∠AOB+∠BOC=90°,∠COD+∠BOC=90°,
所以∠AOB+2∠BOC+∠COD=180°,
即∠AOD+∠BOC=180°,
因为∠BOC=35°,所以∠AOD=145°.
答案:145°
17.如图,将平行四边形ABCD的一边BC延长至E,若∠A=110°,则∠1= .
【解析】因为平行四边形对边平行,所以AD∥BC,AB∥CD.又因为∠A=110°,根据平行线的特征:两直线平行,同旁内角互补,同位角相等,所以∠1=∠B=
180°-∠A=70°.
答案:70°
18.如图,AB∥CD,CD∥EF,∠A=110°,∠E=30°,则∠ACE= .
【解析】因为AB∥CD,∠A=110°,
所以∠ACD=180°-∠A=180°-110°=70°,
因为CD∥EF,∠E=30°,所以∠ECD=∠E=30°,
所以∠ACE=∠ACD-∠ECD=70°-30°=40°.
答案:40°
三、解答题(共7个小题,共58分)
19.已知:线段a,∠α,∠β.
求作:作一个三角形,使其两角分别等于∠α,∠β,且两角所夹的边长为a.
【解析】作法:①作线段AB=a;②过点A作∠CAB=∠α,过点B作∠CBA=∠β,两边交于点C.则△ABC就是要求作的图形.
20.如图,已知直线AB,CD被直线EF所截,如果∠BMN=∠DNF,∠1=∠2,那么MQ∥NP,试写出推理过程.
【解析】因为∠BMN=∠DNF,∠1=∠2,所以∠BMN+∠1=∠DNF+∠2,即∠QMN=
∠PNF,则MQ∥NP.
21.一辆汽车在直线形的公路上由A向B行驶,M,N分别是位于公路AB两侧的学校,如图所示.
(1)汽车在公路上行驶时,会对两个学校的教学都造成影响,当汽车行驶到何处时,分别对两个学校的影响最大 在图上标出来.
(2)当汽车从A向B行驶时,在哪一段上对两个学校的影响越来越大 哪一段上对M学校的影响逐渐减小,而对N学校的影响逐渐增大
【解析】(1)如图,作MC⊥AB于点C,ND⊥AB于点D,根据垂线段最短,所以在点C处对M学校的影响最大,在点D处对N学校的影响最大.
(2)由点A向点C行驶时,对两个学校的影响逐渐增大;由点C向点D行驶时,对M学校的影响逐渐减小,对N学校的影响逐渐增大.
22.如图,∠BAF=46°,∠ACE=136°,CE⊥CD,问CD∥AB吗 为什么
【解析】CD∥AB.
理由:因为∠BAF+∠BAC=180°(邻补角),
∠BAF=46°(已知),
所以∠BAC=180°-∠BAF=180°-46°=134°.
因为CE⊥CD(已知),
所以∠DCE=90°(垂直的性质),
又因为∠FCD+∠DCE+∠ACE=360°,
所以∠FCD=360°-∠DCE-∠ACE
=360°-90°-136°=134°,
所以∠BAC=∠FCD(等量代换),
所以CD∥AB(内错角相等,两直线平行).
23.如图,点P是线段AB的中点,经过点P画BC的平行线交AC于点Q,再经过点Q画AB的平行线,交BC于点S.
(1)用刻度尺度量后确定AQ与QC,CS与BS的长度关系.
(2)用刻度尺度量后确定PQ与BC,QS与AB的长度关系,你发现了什么 用简洁的语言把你发现的规律叙述出来.
【解析】所画的平行线如图所示:
(1)经度量得到AQ=QC,CS=BS.
(2)经度量得到PQ=BC,QS=AB.
经过三角形一边的中点,画另一边的平行线,则这条平行线平分第三边,三角形两边中点之间线段的长度等于第三边长度的一半21*cnjy*com
24.如图,∠B,∠D的两边分别平行.
在图①中,∠B与∠D的数量关系为 .
在图②中,∠B与∠D的数量关系为 .
试分别说明理由,并用一句话归纳结论.
【解析】图①中∠B与∠D相等.理由:
如图(1),因为BE∥DF,所以∠CME=∠D,
因为AB∥DC,所以∠B=∠CME,所以∠B=∠D.
图②中∠B与∠D互补.理由:
如图(2),因为BE∥DF,所以∠BND+∠D=180°,
因为AB∥DC,所以∠B=∠BND,
所以∠B+∠D=180°.
结论:如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补.
25.如图,已知AB∥CD,分别探究下面四个图形中∠APC和∠PAB,∠PCD的关系,请从你所得四个关系中选出任意一个,说明你探究的结论的正确性.
结论:(1) . (2) .
(3) .
(4) .
选择结论: ,说明理由.
【解析】结论:(1)∠PAB+∠APC+∠PCD=360°
(2)∠APC =∠PAB+∠PCD
(3)∠APC =∠PCD-∠PAB
(4)∠APC =∠PAB-∠PCD
选择结论:答案不惟一,
理由:(1)如图(1),过点P作PQ∥AB,因为AB∥CD,所以PQ∥CD,由PQ∥AB可得
∠PAB+∠APQ=180°;由PQ∥CD得∠PCD+∠CPQ=180°,所以∠PAB+∠APQ+∠PCD+∠CPQ=360°,即∠PAB+∠APC+∠PCD=360°.21·cn·jy·com
(2)如图(2),过点P作PQ∥AB,因为AB∥CD,所以PQ∥CD,由PQ∥AB可得∠PAB=∠APQ;由PQ∥CD得∠PCD=∠CPQ,所以∠APC =∠PAB+∠PCD.【来源:21·世纪·教育·网】
(3)因为AB∥CD,所以∠PEB=∠PCD,又因为∠AEP+∠APC+∠PAB=180°,∠PEB+
∠AEP=180°,所以∠APC+∠PAB=∠PCD,
即∠APC =∠PCD-∠PAB.
(4)因为AB∥CD,所以∠PED=∠PAB,又因为∠CEP+∠APC+∠DCP=180°,∠PED+
∠CEP=180°,所以∠APC+∠PCD=∠PAB,
即∠APC =∠PAB-∠PCD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
