4.5 垂线(1)同步练习
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
4.5 垂线(1)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.两条直线相交所成的四个角中,有一个是直角时,就说这两条直线互相垂直,其中的一条直线叫作另一条的垂线,它们的交点叫作垂足;反过来,如果两条直线互相垂直,那么这两条直线 相交所成的四个角都是直角.
2.垂线的性质
在平面内,过一点有且只有一条直线与已知直线垂直.
注意:“有且只有”中,“有”指“存在”,“只有”指“唯一”
“过一点”的点在直线上或直线外都可以.
3.在同一平面内,垂直于同一条直线的两条直线平行;如果一条直线垂直于两平行线中的一条,那么这条直线必垂直于另一条.
基础知识和能力拓展精练
一、选择题
1.画一条线段的垂线,垂足在( )
A. 线段上 B. 线段的端点 C. 线段的延长线上 D. 以上都有可能
2.已知:OA⊥OC,∠AOB∶∠AOC=2∶3,则∠BOC的度数为( ).
A. 30° B. 60° C. 150° D. 30°或150°
3.如图,OA⊥OB,∠BOC=30°,OD平分∠AOC,则∠BOD的大小是( )
A. 20° B. 30° C. 40° D. 60°
4.对于同一平面内的三条直线a,b,c,下列命题中不正确的是( )
A. 若a∥b,b∥c,则a∥c B. 若a⊥b,a⊥c,则b⊥c
C. 若a∥b,a⊥c,则b⊥c D. 若a⊥b,a⊥c,则b∥c
5.下列说法正确的有( )
①不相交的两条直线是平行线;
②经过直线外一点,有且只有一条直线与这条直线平行;
③两条直线被第三条直线所截,同旁内角互补;
④在同一平面内,若直线⊥, ⊥,则直线与不相交.
A. 1个 B. 2个 C. 3个 D. 4个
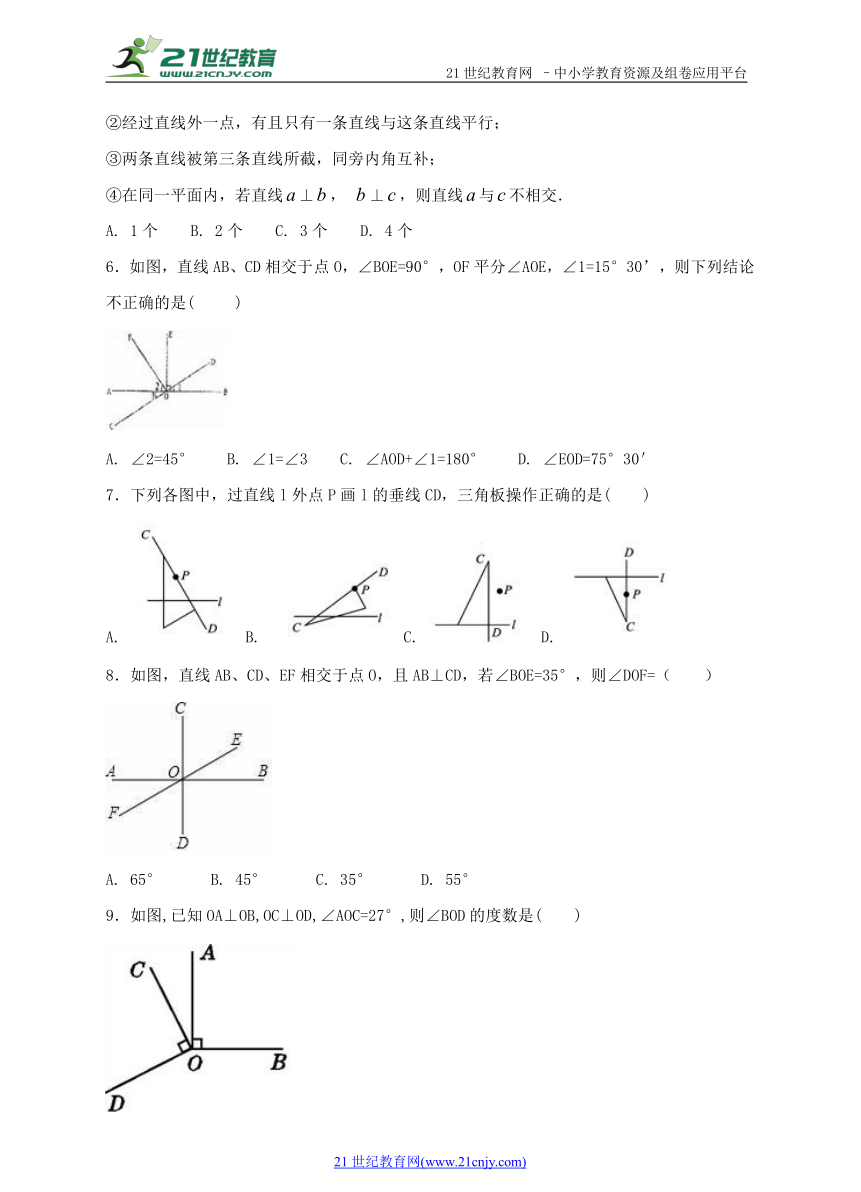
6.如图,直线AB、CD相交于点O,∠BOE=90°,OF平分∠AOE,∠1=15°30’,则下列结论不正确的是( )
A. ∠2=45° B. ∠1=∠3 C. ∠AOD+∠1=180° D. ∠EOD=75°30'
7.下列各图中,过直线l外点P画l的垂线CD,三角板操作正确的是( )
A. B. C. D.
8.如图,直线AB、CD、EF相交于点O,且AB⊥CD,若∠BOE=35°,则∠DOF=( )
A. 65° B. 45° C. 35° D. 55°
9.如图,已知OA⊥OB,OC⊥OD,∠AOC=27°,则∠BOD的度数是( )
A. 117° B. 127° C. 153° D. 163°
10.在同一平面内有直线a1,a2,a3,a4, …, a100,若a1⊥a2,a2∥a3,a3⊥a4,a4∥a5, …,按此规律进行下去,则a1与a100的位置关系是( )
A. 平行 B. 相交 C. 重合 D. 无法判断
二、填空题
11.设a,b,c为平面内三条不同直线:
(1)若a∥b,c⊥a,则b与c的位置关系是______;
(2)若a∥b,b∥c,则a与c的位置关系是______.
12.在同一平面内,OA⊥MN,OB⊥MN,所以OA,OB在同一直线上,理由是________________.
13.如图,直线AB与CD的位置关系是_________,记作_________于点_________,此时∠AOD=_________=_________=_________=90°.
14.如图,直线AB,CD,EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=28°,则∠BOE=____度,∠AOG=____度.
三、解答题
15..如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,求∠2的度数
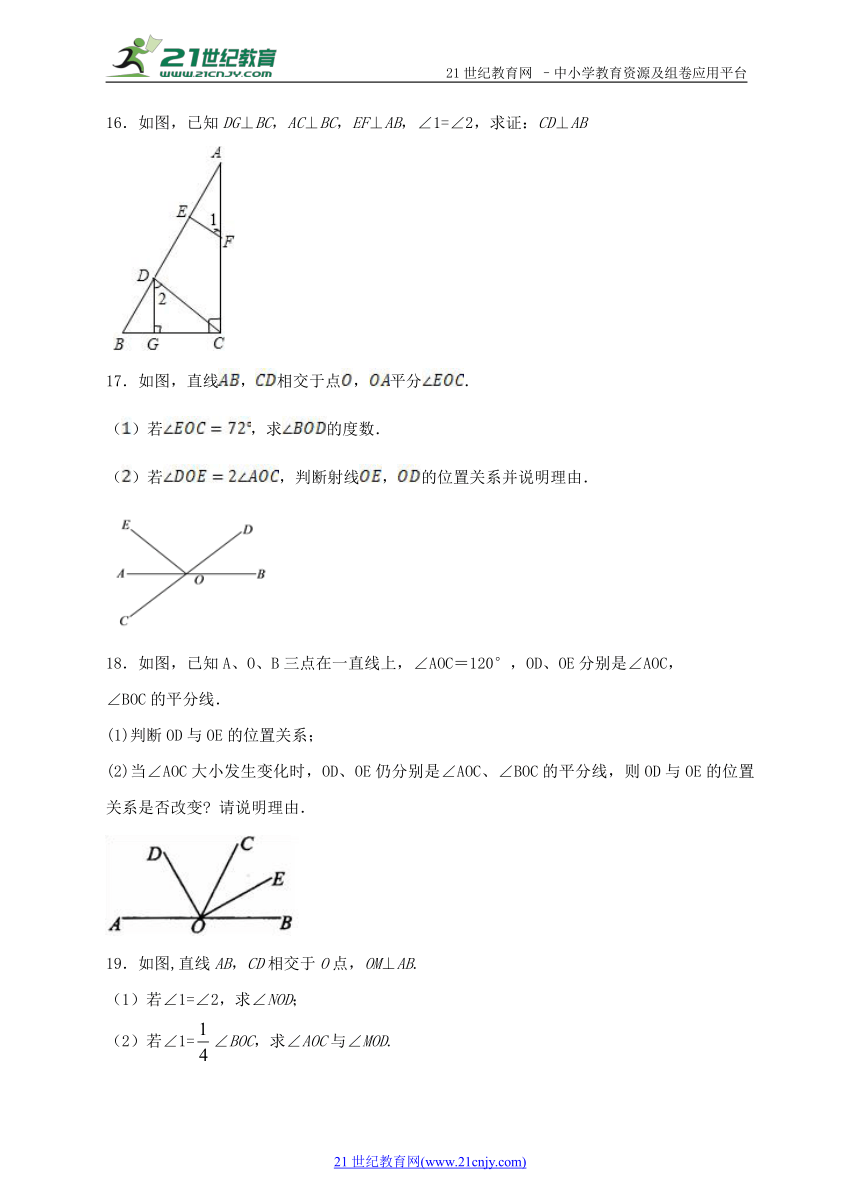
16.如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB
17.如图,直线,相交于点,平分.
()若,求的度数.
()若,判断射线,的位置关系并说明理由.
18.如图,已知A、O、B三点在一直线上,∠AOC=120°,OD、OE分别是∠AOC,
∠BOC的平分线.
(1)判断OD与OE的位置关系;
(2)当∠AOC大小发生变化时,OD、OE仍分别是∠AOC、∠BOC的平分线,则OD与OE的位置关系是否改变 请说明理由.
19.如图,直线AB,CD相交于O点,OM⊥AB.
(1)若∠1=∠2,求∠NOD;
(2)若∠1=∠BOC,求∠AOC与∠MOD.
参考答案
1.D
【解析】解:由垂线的定义可知,画一条线段的垂线,垂足可以在线段上,可以是线段的端点,也可以在线段的延长线上.故选D.
2.D
【解析】∵OA⊥OC,
∴∠AOC=90°,
∵∠AOB:∠AOC=2:3,
∴∠AOB=60°,
因为∠AOB的位置有两种:一种是在∠AOC内,一种是在∠AOC外,
①当在∠AOC内时,∠BOC=90°-60°=30°;
②当在∠AOC外时,∠BOC=90°+60°=150°,
故选D.
3.B
【解析】根据OA⊥OB,∠BOC=30°可求出∠AOC的度数,再根据OD平分∠AOC求出∠DOC的度数,∠DOC与∠BOC作差即可求出∠BOD的度数.
解:∵OA⊥OB,
∴∠BOA=90°,
∵∠BOC=30°,
∴∠AOC=120°,
∵OD平分∠AOC,
∴∠DOC=∠AOC=60°,
∴∠DOC=∠DOC-∠BOC=60°-30°=30°.
故选B.
4.D
【解析】B错误,若a⊥b,a⊥c,则b c
故选B.
5.B
【解析】试题解析:①同一平面内不相交的两条直线是平行线,故错误;
②经过直线外一点,有且只有一条直线与这条直线平行,正确;
③两条平行直线被第三条直线所截,同旁内角互补,故错误;
④在同一平面内,若直线a⊥b,b⊥c,则直线a与c不相交,正确,
故选B.
【点睛】本题考查了命题与定理的知识,解题的关键是能够了解两直线的位置关系、平行线的性质等知识,难度不大.
6.D
【解析】A.∵OE⊥AB于点O,OF平分∠AOE,∴∠2=∠AOE=×90°=45°,本选项正确;
B.∵AB、CD相交于O点,∴∠1=∠3,本选项正确;
C.∵OD过直线AB上一点O,∴∠AOD+∠1=180°,本选项正确;
D.∠1的余角=90°-∠1=90°-15°30’=74°30’,本选项错误;
故选D.
7.D
【解析】解:根据垂线的作法,用直角三角板的一条直角边与l重合,另一条直角边过点P后沿直角边画直线,可得D的画法正确.故选D.
8.D
【解析】∵AB⊥CD,
∴∠BOC=90°,
∵∠BOE=35°,
∴∠COE=∠BOC-∠BOE=90°-35°=55°,
∵直线EF和直线CD相交于点O,
∴∠DOF=∠COE=55°.
故选D.
9.C
【解析】∵OA⊥OB,OC⊥OD,
∴∠AOB=∠DOC=90°,
∵∠BOD=360°-∠AOB-∠DOC-∠AOC, ∠AOC=27°,
∴∠BOD=360°-90°-90°-27°=153°.
故选:C.
10.A
【解析】∵a1⊥a2,a2∥a3,∴a1⊥a3,
∵a3⊥a4,∴a1∥a4.
由此类推:a1⊥a6,a1∥a8
每4条出现重复:与前面的垂直,后面的平行.
∴a1∥a100;
故选A。
点睛:本题考查了平行线,发现规律:每4条出现重复,即与前面的垂直,后面的平行是解题关键。
11. b⊥c a∥c
【解析】(1) ∵a、b、c为平面上三条不同直线,a∥b,c⊥a,
∴b⊥c;
(2) ∵a∥b,b∥c,
∴a∥c
故答案为:b⊥c,a∥c.
12.在同一平面内,过一点有且只有一条直线与已知直线垂直
【解析】因为OA⊥MN,OB⊥MN,所以OA,OB在同一直线上(在同一平面内,过一点有且只有一条直线与已知直线垂直),
故答案为:在同一平面内,过一点有且只有一条直线与已知直线垂直.
13. 垂直; AB⊥CD; O; ∠BOD; ∠BOC; ∠AOC
【解析】试题解析:直线AB与CD的位置关系是垂直,记作AB⊥CD于点O,
此时
故答案为:垂直,AB⊥CD,O,
14. 62 59
【解析】
OG平分
15.解:直线b上在B点右侧一点记为D.
∵a∥b,
∴∠2=∠CBD.
∵AB⊥BC,∠1=55°,
∴∠CBD=90°-55°=35°.
∴∠2=35°.
16.详见解析.
【解析】分析:根据平行线的判定推出DG∥AC,推出∠2=∠1=∠DCA,推出CD∥EF,根据平行线的性质推出CD⊥AB.
本题解析:
证明:∵ DG⊥BC,AC⊥BC(已知),
∴ ∠DGB=∠ACB=90°(垂直的定义),
∴ DG∥AC(同位角相等,两直线平行).
∴ ∠2=∠ACD(两直线平行,内错角相等).
∵ ∠1=∠2(已知),∴ ∠1=∠ACD(等量代换),
∴ EF∥CD(同位角相等,两直线平行).
∴ ∠AEF=∠ADC(两直线平行,同位角相等).
∵ EF⊥AB(已知),∴ ∠AEF=90°(垂直的定义),
∴ ∠ADC=90°(等量代换).
∴ CD⊥AB(垂直的定义).
点睛:本题考查了平行线的性质和判定和垂直定义的应用,主要考查了学生的推理能力.要求学生要牢固掌握平行线的基础含义,能够了然于心,做题时能比较上手.
17.();()
【解析】整体分析:
(1)由角平分线的定义,先求出∠AOC,再由对顶角相等求解;(2)判断出∠DOE=∠COE,即可得到∠DOE=90°.
解:()∵平分且,
∴,
∴.
()射线,的位置关系是垂直.理由如下:
∵平分,
∴,
又∵,
∴,
∵,
∴,
∴.
18.(1)垂直;(2)不变,理由见解析.
【解析】试题分析:(1)OD⊥OE,由∠AOC=120°,可得∠BOC=60°,再根据角平分线的定义可得∠DOC=60°,∠EOC=30°,从而得∠DOE=90°,即OD⊥OE;
(2)不变, 由角平分线的定义可得∠COD=∠AOC,∠COE=∠COB,从而得∠DOE=90°,从而可得OD与OE的位置关系不发生改变.
试题解析:(1)OD⊥OE,理由如下:
∵∠AOC=120°,∴∠BOC=60°,
∵OD是∠AOC的平分线,OE是∠BOC的平分线,
∴∠DOC=60°,∠EOC=30°,
∴∠DOE=60°+30°=90°,
即OD⊥OE;
(2)不变,理由如下:
∵OD,OE分别是∠AOC,∠BOC的平分线,
∴∠COD=∠AOC,∠COE=∠COB,
∴∠DOE= (∠AOC+∠COB)=×180°=90°,
∴OD⊥OE,
即OD与OE的位置关系不发生改变.
【点睛】本题考查了角的计算,考查了角平分线的定义,本题中熟练运用角平分线是解题的关键.
19.(1)90°;(2)∠AOC=60°,∠MOD=150°.
【解析】(1)根据垂直的定义,可得∠AOC+∠1=90°由此易推出∠CON=90°,进而结合平角的定义即可解答本题;
(2)根据垂直可知∠AOM=∠BOM=90°,结合∠1=∠BOC,可得∠1=30°,由此可以得到∠AOC与MOD的度数.
解:(1)∵OM⊥AB,
∴∠AOM=90°,即∠AOC+∠1=90°.
∵∠1=∠2,∠AOC+∠1=90°,
∴∠AOC+∠2=90°,
即∠CON=90°,
∵∠CON+∠NOD=180°,
∴∠NOD=90°.
(2)∵OM⊥AB,
∴∠AOM=∠BOM=90°.
∵∠BOC=∠BOM+∠1,∠BOM=90°,∠1=∠BOC,
∴∠1=30°.
∵∠AOC+∠1=∠AOM=90°,∠1=30°,
∴∠AOC=60°,
∴∠BOD=∠AOC=60°,
∴∠MOD=∠MOB+∠AOC=150°.
点睛:本题主要考查垂线的定义以及角的和差,解题的关键要根据垂直得到90°,再结合角的和、差进行解答.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.5 垂线(1)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.两条直线相交所成的四个角中,有一个是直角时,就说这两条直线互相垂直,其中的一条直线叫作另一条的垂线,它们的交点叫作垂足;反过来,如果两条直线互相垂直,那么这两条直线 相交所成的四个角都是直角.
2.垂线的性质
在平面内,过一点有且只有一条直线与已知直线垂直.
注意:“有且只有”中,“有”指“存在”,“只有”指“唯一”
“过一点”的点在直线上或直线外都可以.
3.在同一平面内,垂直于同一条直线的两条直线平行;如果一条直线垂直于两平行线中的一条,那么这条直线必垂直于另一条.
基础知识和能力拓展精练
一、选择题
1.画一条线段的垂线,垂足在( )
A. 线段上 B. 线段的端点 C. 线段的延长线上 D. 以上都有可能
2.已知:OA⊥OC,∠AOB∶∠AOC=2∶3,则∠BOC的度数为( ).
A. 30° B. 60° C. 150° D. 30°或150°
3.如图,OA⊥OB,∠BOC=30°,OD平分∠AOC,则∠BOD的大小是( )
A. 20° B. 30° C. 40° D. 60°
4.对于同一平面内的三条直线a,b,c,下列命题中不正确的是( )
A. 若a∥b,b∥c,则a∥c B. 若a⊥b,a⊥c,则b⊥c
C. 若a∥b,a⊥c,则b⊥c D. 若a⊥b,a⊥c,则b∥c
5.下列说法正确的有( )
①不相交的两条直线是平行线;
②经过直线外一点,有且只有一条直线与这条直线平行;
③两条直线被第三条直线所截,同旁内角互补;
④在同一平面内,若直线⊥, ⊥,则直线与不相交.
A. 1个 B. 2个 C. 3个 D. 4个
6.如图,直线AB、CD相交于点O,∠BOE=90°,OF平分∠AOE,∠1=15°30’,则下列结论不正确的是( )
A. ∠2=45° B. ∠1=∠3 C. ∠AOD+∠1=180° D. ∠EOD=75°30'
7.下列各图中,过直线l外点P画l的垂线CD,三角板操作正确的是( )
A. B. C. D.
8.如图,直线AB、CD、EF相交于点O,且AB⊥CD,若∠BOE=35°,则∠DOF=( )
A. 65° B. 45° C. 35° D. 55°
9.如图,已知OA⊥OB,OC⊥OD,∠AOC=27°,则∠BOD的度数是( )
A. 117° B. 127° C. 153° D. 163°
10.在同一平面内有直线a1,a2,a3,a4, …, a100,若a1⊥a2,a2∥a3,a3⊥a4,a4∥a5, …,按此规律进行下去,则a1与a100的位置关系是( )
A. 平行 B. 相交 C. 重合 D. 无法判断
二、填空题
11.设a,b,c为平面内三条不同直线:
(1)若a∥b,c⊥a,则b与c的位置关系是______;
(2)若a∥b,b∥c,则a与c的位置关系是______.
12.在同一平面内,OA⊥MN,OB⊥MN,所以OA,OB在同一直线上,理由是________________.
13.如图,直线AB与CD的位置关系是_________,记作_________于点_________,此时∠AOD=_________=_________=_________=90°.
14.如图,直线AB,CD,EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=28°,则∠BOE=____度,∠AOG=____度.
三、解答题
15..如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,求∠2的度数
16.如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB
17.如图,直线,相交于点,平分.
()若,求的度数.
()若,判断射线,的位置关系并说明理由.
18.如图,已知A、O、B三点在一直线上,∠AOC=120°,OD、OE分别是∠AOC,
∠BOC的平分线.
(1)判断OD与OE的位置关系;
(2)当∠AOC大小发生变化时,OD、OE仍分别是∠AOC、∠BOC的平分线,则OD与OE的位置关系是否改变 请说明理由.
19.如图,直线AB,CD相交于O点,OM⊥AB.
(1)若∠1=∠2,求∠NOD;
(2)若∠1=∠BOC,求∠AOC与∠MOD.
参考答案
1.D
【解析】解:由垂线的定义可知,画一条线段的垂线,垂足可以在线段上,可以是线段的端点,也可以在线段的延长线上.故选D.
2.D
【解析】∵OA⊥OC,
∴∠AOC=90°,
∵∠AOB:∠AOC=2:3,
∴∠AOB=60°,
因为∠AOB的位置有两种:一种是在∠AOC内,一种是在∠AOC外,
①当在∠AOC内时,∠BOC=90°-60°=30°;
②当在∠AOC外时,∠BOC=90°+60°=150°,
故选D.
3.B
【解析】根据OA⊥OB,∠BOC=30°可求出∠AOC的度数,再根据OD平分∠AOC求出∠DOC的度数,∠DOC与∠BOC作差即可求出∠BOD的度数.
解:∵OA⊥OB,
∴∠BOA=90°,
∵∠BOC=30°,
∴∠AOC=120°,
∵OD平分∠AOC,
∴∠DOC=∠AOC=60°,
∴∠DOC=∠DOC-∠BOC=60°-30°=30°.
故选B.
4.D
【解析】B错误,若a⊥b,a⊥c,则b c
故选B.
5.B
【解析】试题解析:①同一平面内不相交的两条直线是平行线,故错误;
②经过直线外一点,有且只有一条直线与这条直线平行,正确;
③两条平行直线被第三条直线所截,同旁内角互补,故错误;
④在同一平面内,若直线a⊥b,b⊥c,则直线a与c不相交,正确,
故选B.
【点睛】本题考查了命题与定理的知识,解题的关键是能够了解两直线的位置关系、平行线的性质等知识,难度不大.
6.D
【解析】A.∵OE⊥AB于点O,OF平分∠AOE,∴∠2=∠AOE=×90°=45°,本选项正确;
B.∵AB、CD相交于O点,∴∠1=∠3,本选项正确;
C.∵OD过直线AB上一点O,∴∠AOD+∠1=180°,本选项正确;
D.∠1的余角=90°-∠1=90°-15°30’=74°30’,本选项错误;
故选D.
7.D
【解析】解:根据垂线的作法,用直角三角板的一条直角边与l重合,另一条直角边过点P后沿直角边画直线,可得D的画法正确.故选D.
8.D
【解析】∵AB⊥CD,
∴∠BOC=90°,
∵∠BOE=35°,
∴∠COE=∠BOC-∠BOE=90°-35°=55°,
∵直线EF和直线CD相交于点O,
∴∠DOF=∠COE=55°.
故选D.
9.C
【解析】∵OA⊥OB,OC⊥OD,
∴∠AOB=∠DOC=90°,
∵∠BOD=360°-∠AOB-∠DOC-∠AOC, ∠AOC=27°,
∴∠BOD=360°-90°-90°-27°=153°.
故选:C.
10.A
【解析】∵a1⊥a2,a2∥a3,∴a1⊥a3,
∵a3⊥a4,∴a1∥a4.
由此类推:a1⊥a6,a1∥a8
每4条出现重复:与前面的垂直,后面的平行.
∴a1∥a100;
故选A。
点睛:本题考查了平行线,发现规律:每4条出现重复,即与前面的垂直,后面的平行是解题关键。
11. b⊥c a∥c
【解析】(1) ∵a、b、c为平面上三条不同直线,a∥b,c⊥a,
∴b⊥c;
(2) ∵a∥b,b∥c,
∴a∥c
故答案为:b⊥c,a∥c.
12.在同一平面内,过一点有且只有一条直线与已知直线垂直
【解析】因为OA⊥MN,OB⊥MN,所以OA,OB在同一直线上(在同一平面内,过一点有且只有一条直线与已知直线垂直),
故答案为:在同一平面内,过一点有且只有一条直线与已知直线垂直.
13. 垂直; AB⊥CD; O; ∠BOD; ∠BOC; ∠AOC
【解析】试题解析:直线AB与CD的位置关系是垂直,记作AB⊥CD于点O,
此时
故答案为:垂直,AB⊥CD,O,
14. 62 59
【解析】
OG平分
15.解:直线b上在B点右侧一点记为D.
∵a∥b,
∴∠2=∠CBD.
∵AB⊥BC,∠1=55°,
∴∠CBD=90°-55°=35°.
∴∠2=35°.
16.详见解析.
【解析】分析:根据平行线的判定推出DG∥AC,推出∠2=∠1=∠DCA,推出CD∥EF,根据平行线的性质推出CD⊥AB.
本题解析:
证明:∵ DG⊥BC,AC⊥BC(已知),
∴ ∠DGB=∠ACB=90°(垂直的定义),
∴ DG∥AC(同位角相等,两直线平行).
∴ ∠2=∠ACD(两直线平行,内错角相等).
∵ ∠1=∠2(已知),∴ ∠1=∠ACD(等量代换),
∴ EF∥CD(同位角相等,两直线平行).
∴ ∠AEF=∠ADC(两直线平行,同位角相等).
∵ EF⊥AB(已知),∴ ∠AEF=90°(垂直的定义),
∴ ∠ADC=90°(等量代换).
∴ CD⊥AB(垂直的定义).
点睛:本题考查了平行线的性质和判定和垂直定义的应用,主要考查了学生的推理能力.要求学生要牢固掌握平行线的基础含义,能够了然于心,做题时能比较上手.
17.();()
【解析】整体分析:
(1)由角平分线的定义,先求出∠AOC,再由对顶角相等求解;(2)判断出∠DOE=∠COE,即可得到∠DOE=90°.
解:()∵平分且,
∴,
∴.
()射线,的位置关系是垂直.理由如下:
∵平分,
∴,
又∵,
∴,
∵,
∴,
∴.
18.(1)垂直;(2)不变,理由见解析.
【解析】试题分析:(1)OD⊥OE,由∠AOC=120°,可得∠BOC=60°,再根据角平分线的定义可得∠DOC=60°,∠EOC=30°,从而得∠DOE=90°,即OD⊥OE;
(2)不变, 由角平分线的定义可得∠COD=∠AOC,∠COE=∠COB,从而得∠DOE=90°,从而可得OD与OE的位置关系不发生改变.
试题解析:(1)OD⊥OE,理由如下:
∵∠AOC=120°,∴∠BOC=60°,
∵OD是∠AOC的平分线,OE是∠BOC的平分线,
∴∠DOC=60°,∠EOC=30°,
∴∠DOE=60°+30°=90°,
即OD⊥OE;
(2)不变,理由如下:
∵OD,OE分别是∠AOC,∠BOC的平分线,
∴∠COD=∠AOC,∠COE=∠COB,
∴∠DOE= (∠AOC+∠COB)=×180°=90°,
∴OD⊥OE,
即OD与OE的位置关系不发生改变.
【点睛】本题考查了角的计算,考查了角平分线的定义,本题中熟练运用角平分线是解题的关键.
19.(1)90°;(2)∠AOC=60°,∠MOD=150°.
【解析】(1)根据垂直的定义,可得∠AOC+∠1=90°由此易推出∠CON=90°,进而结合平角的定义即可解答本题;
(2)根据垂直可知∠AOM=∠BOM=90°,结合∠1=∠BOC,可得∠1=30°,由此可以得到∠AOC与MOD的度数.
解:(1)∵OM⊥AB,
∴∠AOM=90°,即∠AOC+∠1=90°.
∵∠1=∠2,∠AOC+∠1=90°,
∴∠AOC+∠2=90°,
即∠CON=90°,
∵∠CON+∠NOD=180°,
∴∠NOD=90°.
(2)∵OM⊥AB,
∴∠AOM=∠BOM=90°.
∵∠BOC=∠BOM+∠1,∠BOM=90°,∠1=∠BOC,
∴∠1=30°.
∵∠AOC+∠1=∠AOM=90°,∠1=30°,
∴∠AOC=60°,
∴∠BOD=∠AOC=60°,
∴∠MOD=∠MOB+∠AOC=150°.
点睛:本题主要考查垂线的定义以及角的和差,解题的关键要根据垂直得到90°,再结合角的和、差进行解答.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
