2018年高考数学(文)三轮复习每日一题2018年4月8日+每周一测
文档属性
| 名称 | 2018年高考数学(文)三轮复习每日一题2018年4月8日+每周一测 | 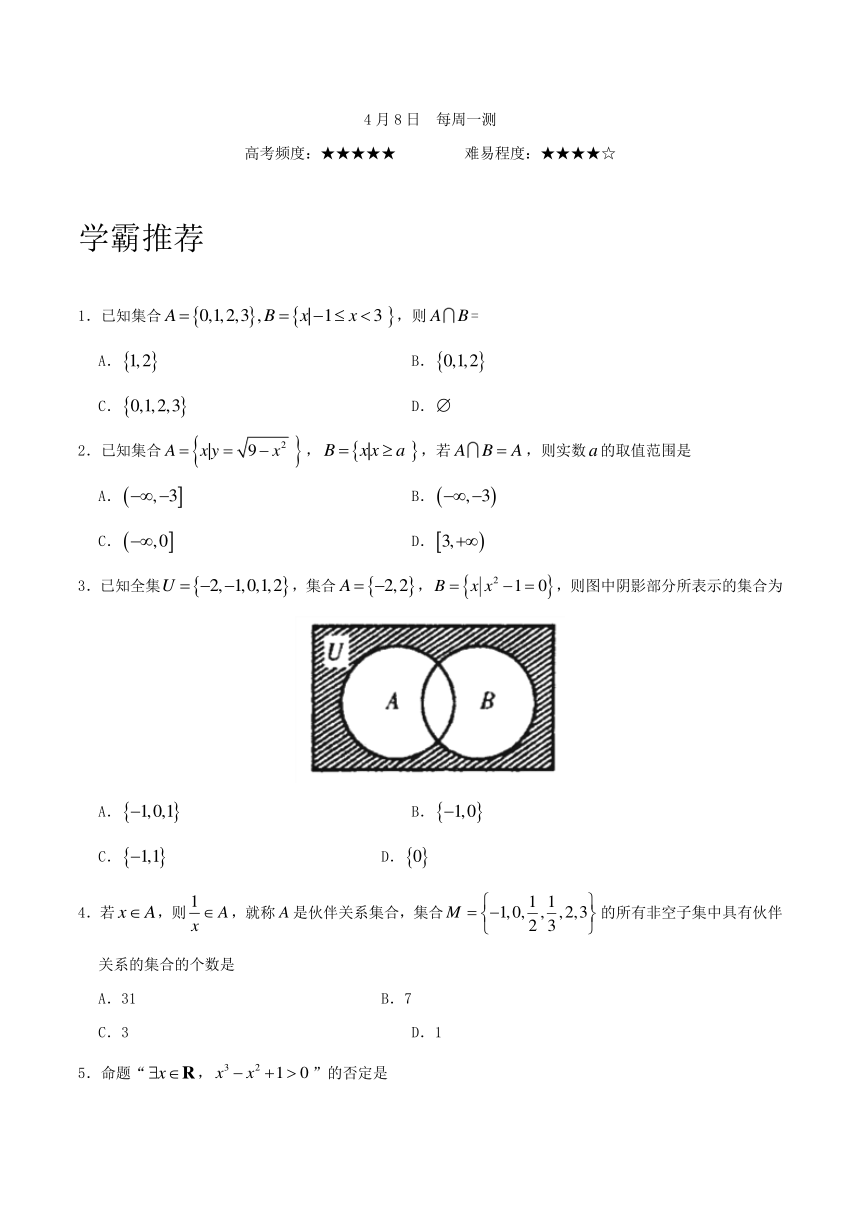 | |
| 格式 | zip | ||
| 文件大小 | 529.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-04 20:49:36 | ||
图片预览





文档简介
4月8日 每周一测
高考频度:★★★★★ 难易程度:★★★★☆
学霸推荐
1.已知集合,则=
A. B.
C. D.
2.已知集合,,若,则实数的取值范围是
A. B.
C. D.
3.已知全集,集合,,则图中阴影部分所表示的集合为
A. B.
C. D.
4.若,则,就称是伙伴关系集合,集合的所有非空子集中具有伙伴关系的集合的个数是
A.31 B.7
C.3 D.1
5.命题“,”的否定是
A., B.,
C., D.不存在,
6.已知,则“”是“是偶函数”的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
7.若是的充分不必要条件,则的取值范围是
A. B.
C. D.
8.已知命题若,,则;命题若,,,则,下列是真命题的是
A. B.
C. D.
9.函数的图象大致为
A. B.
C. D.
10.已知函数为偶函数,当时,,设,,,则
A. B.
C. D.
11.设函数,若互不相等的实数满足,则的取值范围是
A. B.
C. D.
12.已知函数的极大值为4,若函数在上的极小值不大于,则实数的取值范围是
A. B.
C. D.
13.已知定义在上的函数满足恒成立(其中为函数的导函数),则称为函数,例如,便是函数.任给实数,,对于任意的函数,下列不等式一定正确的是
A. B.
C. D.
14.已知函数,则=__________.
15.曲线在点处的切线方程是 ___________.
16.已知函数(为实数).
(1)当曲线与直线切于点时,求,的值;
(2)设,如果在上恒成立,求的取值范围.
17.已知函数.
(1)讨论的单调性;
(2)是否存在实数,使得有三个相异零点?若存在,求出的值;若不存在,说明理由.
1.【答案】B
【解析】由题意得=.故选B.
2.【答案】A
【解析】由已知得,由,得,又,所以.故选A.
4.【答案】B
【解析】集合的所有非空子集中具有伙伴关系的集合为: 故选B.
5.【答案】B
【解析】根据命题的否定知,,的否定为,,故选B.
6.【答案】C
【解析】因为是偶函数,所以,所以.所以“”是“是偶函数”的充要条件.故选C.
7.【答案】D
【解析】解不等式可得:,即是的充分不必要条件,
据此可知:的取值范围是.本题选择D选项.
8.【答案】D
【解析】若,,则 或,故假,真,,,,则,正确,故为真,为假,为真,故选D.
【名师点睛】函数图象的辨识可从以下方面入手:
(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.
(2)从函数的单调性,判断图象的变化趋势.
(3)从函数的奇偶性,判断图象的对称性.
(4)从函数的特征点,排除不合要求的图象.
利用上述方法排除、筛选选项即可顺利解决.
10.【答案】A
【解析】因为在定义域内为增函数,在R上为增函数,所以f(x)在上为增函数,因为函数为偶函数,且,,,故>>,所以,故选A.
11.【答案】B
【解析】画出函数的大致图象如图所示.
不妨令,则,则.结合图象可得,故.
∴.选B.
【名师点睛】解答本题时利用函数图象进行求解,使得解题过程变得直观形象.解题中有两个关键:一是结合图象得到;二是根据图象判断出c的取值范围,进而得到,然后根据不等式的性质可得所求的范围.
12.【答案】B
【名师点睛】本小题主要考查的数学知识是:函数与导数,导数与单调性、极值的关系,考查分类讨论的数学思想方法.涉及函数导数的问题,首先要求函数的定义域,然后求导,令导函数为0,结合函数单调性可得极值,明确极大值和极小值的定义求解.
13.【答案】D
【解析】由题意知,函数在上的每一点处都有导数,且在上恒成立,设在上恒成立,函数在上是增函数,
,,
即,,
两式相加,得,故选D.
【方法点睛】本题主要考查利用导数研究函数的单调性、构造函数比较大小,属于难题.联系已知条件和结论,构造辅助函数是高中数学中一种常用的方法,解题中若遇到有关不等式、方程及最值之类的问题,可设法建立目标函数,并确定变量的限制条件,通过研究函数的单调性、最值等问题,常可使问题变得明了,准确构造出符合题意的函数是解题的关键;解这类不等式的关键点(也是难点)就是构造合适的函数,构造函数时往往从两方面着手:①根据导函数的“形状”变换不等式“形状”;②若是选择题,可根据选项的共性归纳构造恰当的函数.
14.【答案】2
【解析】∵=,∴,故答案为2.
15.【答案】
【解析】∵函数,∴,∴,
∴曲线在点处的切线方程是,即.
故答案为.
【名师点睛】求曲线的切线方程是导数的重要应用之一,用导数求切线方程的关键在于求出切点及斜率,其求法为:设是曲线上的一点,则以为切点的切线方程为.若曲线在点处的切线平行于轴(即导数不存在)时,由切线定义知,切线方程为.
16.【答案】(1),;(2).
【解析】(1),
由曲线与直线切于点,得
解得,.
(2),
∴,且.
①当时,,可知在上单调递增,此时成立;
②当时,,可知在上单调递增,在 上单调递减,此时,不符合条件;
③当时,恒成立,可知在上单调递减,此时成立,不符合条件;
④当时,,可知在上单调递减,此时成立,不符合条件;
⑤当时,,可知在上单调递增,此时成立.
综上所述,,即的取值范围是.
【名师点睛】本小题主要考查导数与切线问题,考查利用导数研究函数的单调性问题,考查了分类讨论的数学思想方法.解答此类问题时,应该首先确定函数的定义域,否则,写出的单调区间易出错;另外,函数的单调区间不能出现“并”的错误写法.分类讨论要做到不重不漏.
(1)根据切点和斜率,列出方程组,解出的值.
(2)化简出的表达式后,求导.注意到,对分类讨论并求函数的单调区间,使得函数的最小值大于,即可求得的取值范围.
17.【答案】(1)见解析;(2)不存在,理由见解析.
【解析】(1)由题可知 .
①当,即时,令得,易知在上单调递减,在上单调递增.
②当,即时,令得或.
当,即时,在,上单调递增,在上单调递减;
当时,,在上单调递增;
当时,在,上单调递增,在上单调递减.
又 ,,
故存在使得,即存在使得.
令,即存在满足.
令,,从而在上单调递增,
所以,
故不存在满足,与假设矛盾,从而不存在使得有三个相异零点.
【名师点睛】(1)求出,分情况讨论的范围,分别令求得的范围,可得函数增区间,求得的范围,可得函数的减区间;
(2)假设有三个相异零点,由(1)的讨论可知,一定有且的极大值大于0,极小值小于0,则取得极大值和极小值时或,注意到此时恒有,则必有为极小值,此时极值点满足,即,还需满足,换元后只需证明即可.
高考频度:★★★★★ 难易程度:★★★★☆
学霸推荐
1.已知集合,则=
A. B.
C. D.
2.已知集合,,若,则实数的取值范围是
A. B.
C. D.
3.已知全集,集合,,则图中阴影部分所表示的集合为
A. B.
C. D.
4.若,则,就称是伙伴关系集合,集合的所有非空子集中具有伙伴关系的集合的个数是
A.31 B.7
C.3 D.1
5.命题“,”的否定是
A., B.,
C., D.不存在,
6.已知,则“”是“是偶函数”的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
7.若是的充分不必要条件,则的取值范围是
A. B.
C. D.
8.已知命题若,,则;命题若,,,则,下列是真命题的是
A. B.
C. D.
9.函数的图象大致为
A. B.
C. D.
10.已知函数为偶函数,当时,,设,,,则
A. B.
C. D.
11.设函数,若互不相等的实数满足,则的取值范围是
A. B.
C. D.
12.已知函数的极大值为4,若函数在上的极小值不大于,则实数的取值范围是
A. B.
C. D.
13.已知定义在上的函数满足恒成立(其中为函数的导函数),则称为函数,例如,便是函数.任给实数,,对于任意的函数,下列不等式一定正确的是
A. B.
C. D.
14.已知函数,则=__________.
15.曲线在点处的切线方程是 ___________.
16.已知函数(为实数).
(1)当曲线与直线切于点时,求,的值;
(2)设,如果在上恒成立,求的取值范围.
17.已知函数.
(1)讨论的单调性;
(2)是否存在实数,使得有三个相异零点?若存在,求出的值;若不存在,说明理由.
1.【答案】B
【解析】由题意得=.故选B.
2.【答案】A
【解析】由已知得,由,得,又,所以.故选A.
4.【答案】B
【解析】集合的所有非空子集中具有伙伴关系的集合为: 故选B.
5.【答案】B
【解析】根据命题的否定知,,的否定为,,故选B.
6.【答案】C
【解析】因为是偶函数,所以,所以.所以“”是“是偶函数”的充要条件.故选C.
7.【答案】D
【解析】解不等式可得:,即是的充分不必要条件,
据此可知:的取值范围是.本题选择D选项.
8.【答案】D
【解析】若,,则 或,故假,真,,,,则,正确,故为真,为假,为真,故选D.
【名师点睛】函数图象的辨识可从以下方面入手:
(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.
(2)从函数的单调性,判断图象的变化趋势.
(3)从函数的奇偶性,判断图象的对称性.
(4)从函数的特征点,排除不合要求的图象.
利用上述方法排除、筛选选项即可顺利解决.
10.【答案】A
【解析】因为在定义域内为增函数,在R上为增函数,所以f(x)在上为增函数,因为函数为偶函数,且,,,故>>,所以,故选A.
11.【答案】B
【解析】画出函数的大致图象如图所示.
不妨令,则,则.结合图象可得,故.
∴.选B.
【名师点睛】解答本题时利用函数图象进行求解,使得解题过程变得直观形象.解题中有两个关键:一是结合图象得到;二是根据图象判断出c的取值范围,进而得到,然后根据不等式的性质可得所求的范围.
12.【答案】B
【名师点睛】本小题主要考查的数学知识是:函数与导数,导数与单调性、极值的关系,考查分类讨论的数学思想方法.涉及函数导数的问题,首先要求函数的定义域,然后求导,令导函数为0,结合函数单调性可得极值,明确极大值和极小值的定义求解.
13.【答案】D
【解析】由题意知,函数在上的每一点处都有导数,且在上恒成立,设在上恒成立,函数在上是增函数,
,,
即,,
两式相加,得,故选D.
【方法点睛】本题主要考查利用导数研究函数的单调性、构造函数比较大小,属于难题.联系已知条件和结论,构造辅助函数是高中数学中一种常用的方法,解题中若遇到有关不等式、方程及最值之类的问题,可设法建立目标函数,并确定变量的限制条件,通过研究函数的单调性、最值等问题,常可使问题变得明了,准确构造出符合题意的函数是解题的关键;解这类不等式的关键点(也是难点)就是构造合适的函数,构造函数时往往从两方面着手:①根据导函数的“形状”变换不等式“形状”;②若是选择题,可根据选项的共性归纳构造恰当的函数.
14.【答案】2
【解析】∵=,∴,故答案为2.
15.【答案】
【解析】∵函数,∴,∴,
∴曲线在点处的切线方程是,即.
故答案为.
【名师点睛】求曲线的切线方程是导数的重要应用之一,用导数求切线方程的关键在于求出切点及斜率,其求法为:设是曲线上的一点,则以为切点的切线方程为.若曲线在点处的切线平行于轴(即导数不存在)时,由切线定义知,切线方程为.
16.【答案】(1),;(2).
【解析】(1),
由曲线与直线切于点,得
解得,.
(2),
∴,且.
①当时,,可知在上单调递增,此时成立;
②当时,,可知在上单调递增,在 上单调递减,此时,不符合条件;
③当时,恒成立,可知在上单调递减,此时成立,不符合条件;
④当时,,可知在上单调递减,此时成立,不符合条件;
⑤当时,,可知在上单调递增,此时成立.
综上所述,,即的取值范围是.
【名师点睛】本小题主要考查导数与切线问题,考查利用导数研究函数的单调性问题,考查了分类讨论的数学思想方法.解答此类问题时,应该首先确定函数的定义域,否则,写出的单调区间易出错;另外,函数的单调区间不能出现“并”的错误写法.分类讨论要做到不重不漏.
(1)根据切点和斜率,列出方程组,解出的值.
(2)化简出的表达式后,求导.注意到,对分类讨论并求函数的单调区间,使得函数的最小值大于,即可求得的取值范围.
17.【答案】(1)见解析;(2)不存在,理由见解析.
【解析】(1)由题可知 .
①当,即时,令得,易知在上单调递减,在上单调递增.
②当,即时,令得或.
当,即时,在,上单调递增,在上单调递减;
当时,,在上单调递增;
当时,在,上单调递增,在上单调递减.
又 ,,
故存在使得,即存在使得.
令,即存在满足.
令,,从而在上单调递增,
所以,
故不存在满足,与假设矛盾,从而不存在使得有三个相异零点.
【名师点睛】(1)求出,分情况讨论的范围,分别令求得的范围,可得函数增区间,求得的范围,可得函数的减区间;
(2)假设有三个相异零点,由(1)的讨论可知,一定有且的极大值大于0,极小值小于0,则取得极大值和极小值时或,注意到此时恒有,则必有为极小值,此时极值点满足,即,还需满足,换元后只需证明即可.
同课章节目录
