第9章 中心对称图形——平行四边形期中复习提优测试题
文档属性
| 名称 | 第9章 中心对称图形——平行四边形期中复习提优测试题 |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-05 11:05:49 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
期中复习(二)
平行四边形提优复习
一.填空题
1.如图1,P是菱形ABCD对角线BD上一点,PE⊥AB于点E,PE=4cm,则点P到BC的距离 是________cm. 21世纪教育网版权所有
图1 图2
2.已知平行四边形三个顶点是(3,-2),(5,2),(-1,4),第四个顶点的坐标为_________
3.如图2,已知△ABC的周长为1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形,…,依此类推,则第10个三角形的周长为 .21·cn·jy·com
4.如图3,直角三角形ABC中,∠ACB=90°,AB=10,AC:AB=3:5,点O是AB的中点,∠DOE=∠A,当∠DOE以点O为旋转中心旋转时,OD交AC的延长线于点D,交边CB于点M,OE交线段BM于点N.CM=2,则线段CD的长为_________;
5.如图4,菱形ABCD中,AB=4,∠ABC=60°,点E、F、G分别为线段BC,CD,BD上的任意一点,则EG+FG的最小值为________
图3 图4
二.选择题
6.如图5,Rt△ABC中,∠BAC=90°,∠B=60°,△ABˊCˊ可以由△ABC绕点A顺时针旋转90°得到(点B'与点B是对应点,点C'与点C是对应点),连接CC',则∠CCˊBˊ的度数是 ( )
A.45° B.30° C.25° D.15°
7.如图6,点D、E、F分别是△ABC三边的中点,则下列判断错误的是 ( )
A.四边形AEDF一定是平行四边形
B.若∠A=90°,则四边形AEDF是矩形
C.若AD平分∠A,则四边形AEDF是正方形
D.若AD⊥BC,则四边形AEDF是菱形
图5 图6
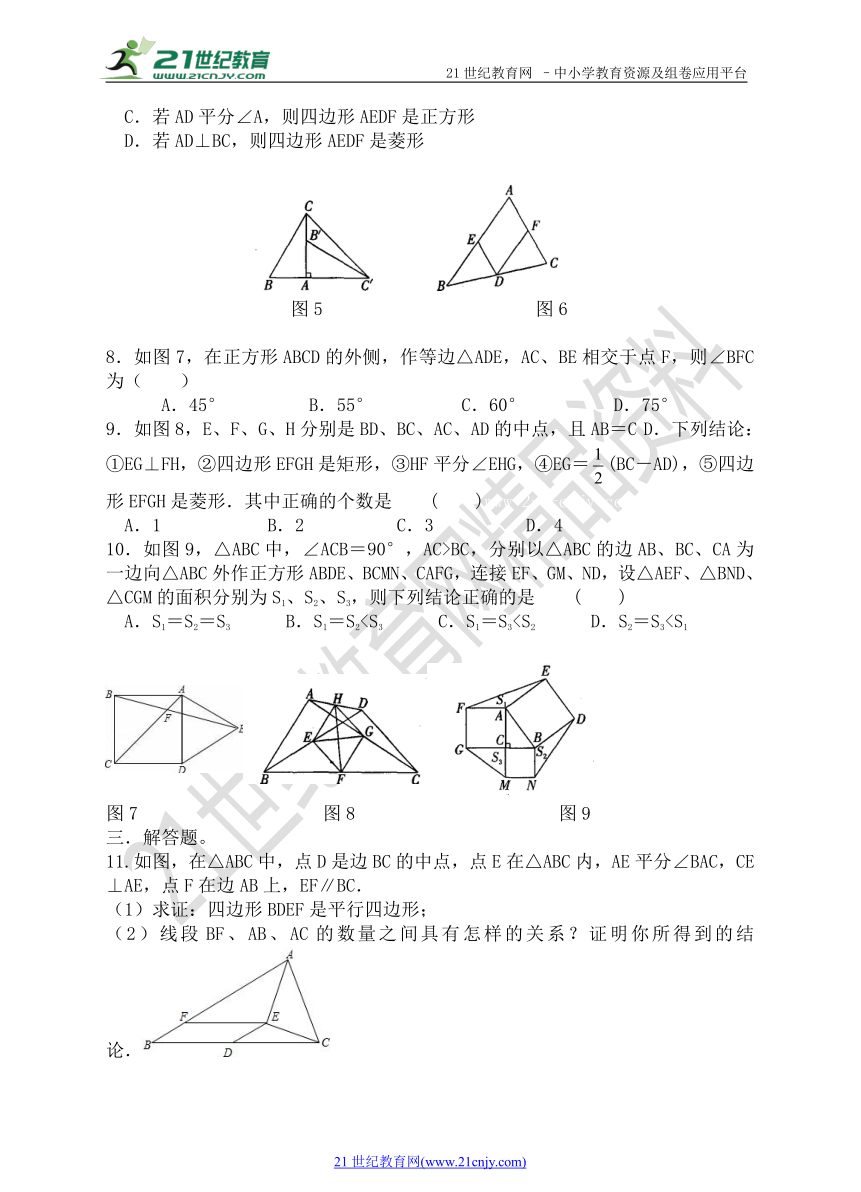
8.如图7,在正方形ABCD的外侧,作等边△ADE,AC、BE相交于点F,则∠BFC为( )
A.45° B.55° C.60° D.75°
9.如图8,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=C D.下列结论:①EG⊥FH,②四边形EFGH是矩形,③HF平分∠EHG,④EG=(BC-AD),⑤四边形EFGH是菱形.其中正确的个数是 ( )www-2-1-cnjy-com
A.1 B.2 C.3 D.4
10.如图9,△ABC中,∠ACB=90°,AC>BC,分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,连接EF、GM、ND,设△AEF、△BND、△CGM的面积分别为S1、S2、S3,则下列结论正确的是 ( )
A.S1=S2=S3 B.S1=S2图7 图8 图9
三.解答题。
11.如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.
(1)求证:四边形BDEF是平行四边形;
(2)线段BF、AB、AC的数量之间具有怎样的关系?证明你所得到的结论.【来源:21cnj*y.co*m】
12.已知:如图,在菱形ABCD中,∠B=60°,点E,F分别是AB,AD上的两个动点,且始终保持∠ECF=60°
(1)试判断△ECF的形状并说明理由;若把∠ECF=60°换成AE=DF,其它条件不变,结论还成立吗?
(2)若菱形的边长为6cm,那么△ECF的周长是否存在最小值 如果存在,请求出来,如果不存在请说明理由.【出处:21教育名师】
13.如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.【版权所有:21教育】
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,当G点在何位置时四边形AEBD是矩形?请说明理由并求出点H的坐标.21*cnjy*com
14.类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.(1)概念,如图1,在四边形ABCD中,添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件,你添加的条件是___.
(2)问题探究:
①小红猜想:对角线互相平分的“等邻边四边形”是菱形.她的猜想正确吗?请说明理由。
②如图2,在“等邻边四边形”ABCD中,∠DAB=60°,∠ABC=∠ADC=90°,AB=AD=6,求对角线AC的长.
(3)拓展应用:如图3,“等邻边四边形”ABCD中,AB=AD,∠BAD=60°,∠BCD=30°,AC为对角线,试探究AC,BC,DC的数量关系.21*cnjy*com
15.如图,已知菱形ABCD,点P、Q在直线BD上,点P在点Q左侧,AP∥CQ.
(1)如图1,当∠ABC=90°,点P、Q在线段BD上时,求证:BP+BQ=BA;
(2)如图2,当∠ABC=60°,点P在线段DB的延长线上时,试探究BP、BQ、BA之间的数量关系,并说明理由.2-1-c-n-j-y
16.以四边形ABCD的边AB,BC,CD,DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E,F,G,H,顺次连接这四个点,得到四边形EFGH.
(1)如图①,当四边形ABCD为正方形时,我们发现四边形EFGH也是正方形;如图②,当四边形ABCD为矩形时,请判断四边形EFGH的形状(不要求证明).
(2)如图③,当四边形ABCD为一般平行四边形时,设∠ADC=α(0°<α<90°).
①试用含α的代数式表示∠HAE;
②求证:HE=HG.
③四边形EFGH是什么四边形?并说明理由.
17.已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.www.21-cn-jy.com
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.
参考答案:
一.填空题
1. 4 2. (9,-4),(-3,0)或(1,8)
3. 4. 3 5.
二.选择题
6—10:D C C C A
三.解答题
11.如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.
(1)求证:四边形BDEF是平行四边形;
(2)线段BF、AB、AC的数量之间具有怎样的关系?证明你所得到的结论.
解:(1)延长CE交AB与G
∵AE⊥CG,AE平分∠BAC
∴△AGE是等腰三角形
∴E是GC的中点
∵D是CB的中点
∴DE//AB
∴DE//BF
∵EF//BD
∴四边形BDEF是平行四边形
(2)2BF+AC=AB,
由(1)知DE是△BCG的中位线
四边形BDEF是平行四边形
∴BF=DE,DE=BG
∴BF=BG
∴BF=FG
∴AB=AG+FG+BF=AC+2BF
即2BF+AC=AB
12. 已知:如图,在菱形ABCD中,∠B=60°,点E,F分别是AB,AD上的两个动点,且始终保持∠ECF=60°
(1)①试判断△ECF的形状并说明理由;②若把∠ECF=60°换成AE=DF,其它条件不变,结论还成立吗?
(2)若菱形的边长为6cm,那么△ECF的周长是否存在最小值 如果存在,请求出来,如果不存在请说明理由.21教育名师原创作品
解:(1)①连接AC,
∵ABCD是菱形,
∴AB=BC=DC,∠B=∠D,
∵∠B=60°,
∴ΔABC是等边三角形,∴
∴AC=BC=CD=AD,
∴ΔACD是等边三角形,
∴ΔACE≌ΔDCF,
∴CE=CF,
∵∠ECF=60°
∴ΔCEF是等边三角形.
②成立
⑵∵ΔACE≌ΔDCF,∴∠ACE=∠DCF,∴∠ECF=∠ACE+∠ACF=∠ACF+∠DCF=60°,
∴ΔCEF是等边三角形,
当CE最小时ΔCEF周长最小,
∴CE⊥AB,这时,CE==
∴ΔCEF周长最小=
13.如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,当G点在何位置时四边形AEBD是矩形?请说明理由并求出点H的坐标.
解:(1)证明:∵正方形ABCO绕点C旋转得到正方形CDEF
∴CD=CB,∠CDG=∠CBG=90°
在Rt△CDG和Rt△CBG中
∴△CDG≌△CBG(HL),
(2)∵△CDG≌△CBG
∴∠DCG=∠BCG,DG=BG
在Rt△CHO和Rt△CHD中
∴△CHO≌△CHD(HL)
∴∠OCH=∠DCH,OH=DH
∴∠HCG=∠HCD+∠GCD= ∠OCD+∠DCB
= ∠OCB=45°
HG=HD+DG=HO+BG
(3)G为AB中点的时四边形AEBD可为矩形
如图,
连接BD、DA、AE、EB
因为四边形AEBD若为矩形,则需先为平行四边形,即要对角线互相平分,合适的点只有G为AB中点的时候.
因为DG=BG,所以此时同时满足DG=AG=EG=BG,即平行四边形AEBD对角线相等,则其为矩形.
所以当G点为AB中点时,四边形AEBD为矩形.
∵四边形DAEB为矩形
∴AG=EG=BG=DG
∵AB=6
∴AG=BG=3
设H点的坐标为(x,0)
则HO=x
∵OH=DH,BG=DG
∴HD=x,DG=3
在Rt△HGA中
∵HG=x+3,GA=3,HA=6-x
∴(x+3)2=32+(6-x)2
∴x=2
∴H点的坐标为(2,0).
14.类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)概念,如图1,在四边形ABCD中,添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件,你添加的条件是___.
(2)问题探究:
①小红猜想:对角线互相平分的“等邻边四边形”是菱形.她的猜想正确吗?请说明理由。
②如图2,在“等邻边四边形”ABCD中,∠DAB=60°,∠ABC=∠ADC=90°,AB=AD=6,求对角线AC的长.
(3)拓展应用:如图3,“等邻边四边形”ABCD中,AB=AD,∠BAD=60°,∠BCD=30°,AC为对角线,试探究AC,BC,DC的数量关系.
解:.(1)根据定义:AB=BC.
(2)
①正确
理由如下:∵四边形的对角线互相平分,
∴这个四边形是平行四边形,小红的结论正确.
∵四边形是“等邻边四边形”,
∴这个四边形有一组邻边相等,
∴这个“等邻边四边形”是菱形,
②连接AC、BD交于点O,
∵AB=AD,∠BAD=60°,
∴△ABD是等边三角形,
∴∠ABD=∠ADB=60°,
∵∠ABC=∠ADC=90°,
∴∠CBD=∠CDB=30°,
∴CB=CD,
∴AC垂直平分BD,
直角△ABC中
AC=
(3)过点C作CE⊥BC于点C,且使得CE=CD,
∵∠BAD+∠BCD=90°,
∴∠DCE=60°,
∴△CDE是等边三角形,
∴DE=CD,∠EDC=60°,
∵AB=AD,∠DAB=60°,
∴△ABD是等边三角形,
∴AD=BD,∠ADB=60°,
在△ADC和△BDE中,
AD=BD∠ADC=∠BDECD=DE
∴△ADC≌△BDE(SAS),
∴AC=BE,
∵∠BCE=90°,
∴BE2=BC2+CE2,
即AC2=BC2+CD2
15.如图,已知菱形ABCD,点P、Q在直线BD上,点P在点Q左侧,AP∥CQ.
(1)如图1,当∠ABC=90°,点P、Q在线段BD上时,求证:BP+BQ=BA;
(2)如图2,当∠ABC=60°,点P在线段DB的延长线上时,试探究BP、BQ、BA之间的数量关系,并说明理由.
解:(1)证明:∵四边形ABCD是菱形,
∴AB=CD,AB∥CD,
∴∠ABP=∠CDQ,
∵AP∥CQ,
∴∠APD=∠CQB,
∴∠APB=∠CQD,
在△ABP和CDQ中,
,
∴△ABP≌CDQ,
∴BP=DQ.
(2)∵∠ABC=90°,
∴菱形ABCD为正方形,
∴∠ABD=45°,∠BAD=90°,
∴在RT△ABD中,由勾股定理得:BD=BA,
由(1)得 BP=DQ,
∴BP+BQ=DQ+BQ=BD,
∴BP+BQ=BA.
(3)BP、BQ、BA之间的数量关系BQ-BP=BA,
理由如下:连接AC交BD于点H,
∵四边形ABCD是菱形,∠ABC=60°,
∴∠ABH=30°,∠AHB=90°,BD=2BH,
∴BH=AB cos∠ABH=BA,
由(1)得,BP=DQ,
∴BQ-BP=BQ-DQ=BD=BA.
16.以四边形ABCD的边AB,BC,CD,DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E,F,G,H,顺次连接这四个点,得到四边形EFGH.
(1)如图①,当四边形ABCD为正方形时,我们发现四边形EFGH也是正方形;如图②,当四边形ABCD为矩形时,请判断四边形EFGH的形状(不要求证明).
(2)如图③,当四边形ABCD为一般平行四边形时,设∠ADC=α(0°<α<90°).
①试用含α的代数式表示∠HAE;
②求证:HE=HG.
③四边形EFGH是什么四边形?并说明理由.
解:(1)解:四边形EFGH是正方形.
(2)①解:在□ABCD中,AB∥CD,所以∠BAD=180°-∠ADC=180°-α.因为△HAD和△EAB都是等腰直角三角形,所以∠HAD=∠EAB=45°.
所以∠HAE=360°-∠HAD-∠EAB-∠BAD=360°-45°-45°-(180°-α)
=90°+α.
②证明:因为△AEB和△DGC都是等腰直角三角形
所以AE=AB,DG=CD.
在□ABCD中,AB=CD,
所以AE=DG.
因为△HAD和△GDC都是等腰直角三角形
所以∠HDA=∠CDG=45°.
所以∠HDG=∠HDA+∠ADC+∠CDG=45°+α+45°=90°+α=∠HAE.
又HA=HD,
所以△HAE≌△HDG,所以HE=HG.
③解:四边形EFGH是正方形.
理由:同②,得GH=GF,FG=FE.
因为HE=HG,所以GH=GF=EF=HE.
所以四边形EFGH是菱形.
因为△HAE≌△HDG,
所以∠DHG=∠AHE.
因为∠AHD=∠AHG+∠DHG=90°,
所以∠EHG=∠AHG+∠AHE=90°.
所以四边形EFGH是正方形.
17.已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.21cnjy.com
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.2·1·c·n·j·y
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.
解:(1)①∵四边形ABCD是矩形,
∴AD∥BC,
∴∠CAD=∠ACB,∠AEF=∠CFE,
∵EF垂直平分AC,垂足为O,
∴OA=OC,
∴△AOE≌△COF,
∴OE=OF,
∴四边形AFCE为平行四边形,
又∵EF⊥AC,
∴四边形AFCE为菱形,
②设菱形的边长AF=CF=xcm,则BF=(8﹣x)cm,
在Rt△ABF中,AB=4cm,
由勾股定理得42+(8﹣x)2=x2,
解得x=5,
∴AF=5cm;
(2)①显然当P点在AF上时,Q点在CD上,此时A、C、P、Q四点不可能构成平行四边形;
同理P点在AB上时,Q点在DE或CE上,也不能构成平行四边形,
因此只有当P点在BF上、Q点在ED上时,才能构成平行四边形,
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,PC=QA,
∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,
∴PC=5t,QA=12﹣4t,
∴5t=12﹣4t,
解得,
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,秒,
②由题意得,以A、C、P、Q四点为顶点的四边形是平行四边形时,点P、Q在互相平行的对应边上,
分三种情况:
(i)如图1,当P点在AF上、Q点在CE上时,AP=CQ,即a=12﹣b,得a+b=12
(ii)如图2,当P点在BF上、Q点在DE上时,AQ=CP,即12﹣b=a,得a+b=12
(iii)如图3,当P点在AB上、Q点在CD上时,AP=CQ,即12﹣a=b,得a+b=12,
综上所述,a与b满足的数量关系式是a+b=12(ab≠0)。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期中复习(二)
平行四边形提优复习
一.填空题
1.如图1,P是菱形ABCD对角线BD上一点,PE⊥AB于点E,PE=4cm,则点P到BC的距离 是________cm. 21世纪教育网版权所有
图1 图2
2.已知平行四边形三个顶点是(3,-2),(5,2),(-1,4),第四个顶点的坐标为_________
3.如图2,已知△ABC的周长为1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形,…,依此类推,则第10个三角形的周长为 .21·cn·jy·com
4.如图3,直角三角形ABC中,∠ACB=90°,AB=10,AC:AB=3:5,点O是AB的中点,∠DOE=∠A,当∠DOE以点O为旋转中心旋转时,OD交AC的延长线于点D,交边CB于点M,OE交线段BM于点N.CM=2,则线段CD的长为_________;
5.如图4,菱形ABCD中,AB=4,∠ABC=60°,点E、F、G分别为线段BC,CD,BD上的任意一点,则EG+FG的最小值为________
图3 图4
二.选择题
6.如图5,Rt△ABC中,∠BAC=90°,∠B=60°,△ABˊCˊ可以由△ABC绕点A顺时针旋转90°得到(点B'与点B是对应点,点C'与点C是对应点),连接CC',则∠CCˊBˊ的度数是 ( )
A.45° B.30° C.25° D.15°
7.如图6,点D、E、F分别是△ABC三边的中点,则下列判断错误的是 ( )
A.四边形AEDF一定是平行四边形
B.若∠A=90°,则四边形AEDF是矩形
C.若AD平分∠A,则四边形AEDF是正方形
D.若AD⊥BC,则四边形AEDF是菱形
图5 图6
8.如图7,在正方形ABCD的外侧,作等边△ADE,AC、BE相交于点F,则∠BFC为( )
A.45° B.55° C.60° D.75°
9.如图8,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=C D.下列结论:①EG⊥FH,②四边形EFGH是矩形,③HF平分∠EHG,④EG=(BC-AD),⑤四边形EFGH是菱形.其中正确的个数是 ( )www-2-1-cnjy-com
A.1 B.2 C.3 D.4
10.如图9,△ABC中,∠ACB=90°,AC>BC,分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,连接EF、GM、ND,设△AEF、△BND、△CGM的面积分别为S1、S2、S3,则下列结论正确的是 ( )
A.S1=S2=S3 B.S1=S2
三.解答题。
11.如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.
(1)求证:四边形BDEF是平行四边形;
(2)线段BF、AB、AC的数量之间具有怎样的关系?证明你所得到的结论.【来源:21cnj*y.co*m】
12.已知:如图,在菱形ABCD中,∠B=60°,点E,F分别是AB,AD上的两个动点,且始终保持∠ECF=60°
(1)试判断△ECF的形状并说明理由;若把∠ECF=60°换成AE=DF,其它条件不变,结论还成立吗?
(2)若菱形的边长为6cm,那么△ECF的周长是否存在最小值 如果存在,请求出来,如果不存在请说明理由.【出处:21教育名师】
13.如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.【版权所有:21教育】
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,当G点在何位置时四边形AEBD是矩形?请说明理由并求出点H的坐标.21*cnjy*com
14.类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.(1)概念,如图1,在四边形ABCD中,添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件,你添加的条件是___.
(2)问题探究:
①小红猜想:对角线互相平分的“等邻边四边形”是菱形.她的猜想正确吗?请说明理由。
②如图2,在“等邻边四边形”ABCD中,∠DAB=60°,∠ABC=∠ADC=90°,AB=AD=6,求对角线AC的长.
(3)拓展应用:如图3,“等邻边四边形”ABCD中,AB=AD,∠BAD=60°,∠BCD=30°,AC为对角线,试探究AC,BC,DC的数量关系.21*cnjy*com
15.如图,已知菱形ABCD,点P、Q在直线BD上,点P在点Q左侧,AP∥CQ.
(1)如图1,当∠ABC=90°,点P、Q在线段BD上时,求证:BP+BQ=BA;
(2)如图2,当∠ABC=60°,点P在线段DB的延长线上时,试探究BP、BQ、BA之间的数量关系,并说明理由.2-1-c-n-j-y
16.以四边形ABCD的边AB,BC,CD,DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E,F,G,H,顺次连接这四个点,得到四边形EFGH.
(1)如图①,当四边形ABCD为正方形时,我们发现四边形EFGH也是正方形;如图②,当四边形ABCD为矩形时,请判断四边形EFGH的形状(不要求证明).
(2)如图③,当四边形ABCD为一般平行四边形时,设∠ADC=α(0°<α<90°).
①试用含α的代数式表示∠HAE;
②求证:HE=HG.
③四边形EFGH是什么四边形?并说明理由.
17.已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.www.21-cn-jy.com
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.
参考答案:
一.填空题
1. 4 2. (9,-4),(-3,0)或(1,8)
3. 4. 3 5.
二.选择题
6—10:D C C C A
三.解答题
11.如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.
(1)求证:四边形BDEF是平行四边形;
(2)线段BF、AB、AC的数量之间具有怎样的关系?证明你所得到的结论.
解:(1)延长CE交AB与G
∵AE⊥CG,AE平分∠BAC
∴△AGE是等腰三角形
∴E是GC的中点
∵D是CB的中点
∴DE//AB
∴DE//BF
∵EF//BD
∴四边形BDEF是平行四边形
(2)2BF+AC=AB,
由(1)知DE是△BCG的中位线
四边形BDEF是平行四边形
∴BF=DE,DE=BG
∴BF=BG
∴BF=FG
∴AB=AG+FG+BF=AC+2BF
即2BF+AC=AB
12. 已知:如图,在菱形ABCD中,∠B=60°,点E,F分别是AB,AD上的两个动点,且始终保持∠ECF=60°
(1)①试判断△ECF的形状并说明理由;②若把∠ECF=60°换成AE=DF,其它条件不变,结论还成立吗?
(2)若菱形的边长为6cm,那么△ECF的周长是否存在最小值 如果存在,请求出来,如果不存在请说明理由.21教育名师原创作品
解:(1)①连接AC,
∵ABCD是菱形,
∴AB=BC=DC,∠B=∠D,
∵∠B=60°,
∴ΔABC是等边三角形,∴
∴AC=BC=CD=AD,
∴ΔACD是等边三角形,
∴ΔACE≌ΔDCF,
∴CE=CF,
∵∠ECF=60°
∴ΔCEF是等边三角形.
②成立
⑵∵ΔACE≌ΔDCF,∴∠ACE=∠DCF,∴∠ECF=∠ACE+∠ACF=∠ACF+∠DCF=60°,
∴ΔCEF是等边三角形,
当CE最小时ΔCEF周长最小,
∴CE⊥AB,这时,CE==
∴ΔCEF周长最小=
13.如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,当G点在何位置时四边形AEBD是矩形?请说明理由并求出点H的坐标.
解:(1)证明:∵正方形ABCO绕点C旋转得到正方形CDEF
∴CD=CB,∠CDG=∠CBG=90°
在Rt△CDG和Rt△CBG中
∴△CDG≌△CBG(HL),
(2)∵△CDG≌△CBG
∴∠DCG=∠BCG,DG=BG
在Rt△CHO和Rt△CHD中
∴△CHO≌△CHD(HL)
∴∠OCH=∠DCH,OH=DH
∴∠HCG=∠HCD+∠GCD= ∠OCD+∠DCB
= ∠OCB=45°
HG=HD+DG=HO+BG
(3)G为AB中点的时四边形AEBD可为矩形
如图,
连接BD、DA、AE、EB
因为四边形AEBD若为矩形,则需先为平行四边形,即要对角线互相平分,合适的点只有G为AB中点的时候.
因为DG=BG,所以此时同时满足DG=AG=EG=BG,即平行四边形AEBD对角线相等,则其为矩形.
所以当G点为AB中点时,四边形AEBD为矩形.
∵四边形DAEB为矩形
∴AG=EG=BG=DG
∵AB=6
∴AG=BG=3
设H点的坐标为(x,0)
则HO=x
∵OH=DH,BG=DG
∴HD=x,DG=3
在Rt△HGA中
∵HG=x+3,GA=3,HA=6-x
∴(x+3)2=32+(6-x)2
∴x=2
∴H点的坐标为(2,0).
14.类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)概念,如图1,在四边形ABCD中,添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件,你添加的条件是___.
(2)问题探究:
①小红猜想:对角线互相平分的“等邻边四边形”是菱形.她的猜想正确吗?请说明理由。
②如图2,在“等邻边四边形”ABCD中,∠DAB=60°,∠ABC=∠ADC=90°,AB=AD=6,求对角线AC的长.
(3)拓展应用:如图3,“等邻边四边形”ABCD中,AB=AD,∠BAD=60°,∠BCD=30°,AC为对角线,试探究AC,BC,DC的数量关系.
解:.(1)根据定义:AB=BC.
(2)
①正确
理由如下:∵四边形的对角线互相平分,
∴这个四边形是平行四边形,小红的结论正确.
∵四边形是“等邻边四边形”,
∴这个四边形有一组邻边相等,
∴这个“等邻边四边形”是菱形,
②连接AC、BD交于点O,
∵AB=AD,∠BAD=60°,
∴△ABD是等边三角形,
∴∠ABD=∠ADB=60°,
∵∠ABC=∠ADC=90°,
∴∠CBD=∠CDB=30°,
∴CB=CD,
∴AC垂直平分BD,
直角△ABC中
AC=
(3)过点C作CE⊥BC于点C,且使得CE=CD,
∵∠BAD+∠BCD=90°,
∴∠DCE=60°,
∴△CDE是等边三角形,
∴DE=CD,∠EDC=60°,
∵AB=AD,∠DAB=60°,
∴△ABD是等边三角形,
∴AD=BD,∠ADB=60°,
在△ADC和△BDE中,
AD=BD∠ADC=∠BDECD=DE
∴△ADC≌△BDE(SAS),
∴AC=BE,
∵∠BCE=90°,
∴BE2=BC2+CE2,
即AC2=BC2+CD2
15.如图,已知菱形ABCD,点P、Q在直线BD上,点P在点Q左侧,AP∥CQ.
(1)如图1,当∠ABC=90°,点P、Q在线段BD上时,求证:BP+BQ=BA;
(2)如图2,当∠ABC=60°,点P在线段DB的延长线上时,试探究BP、BQ、BA之间的数量关系,并说明理由.
解:(1)证明:∵四边形ABCD是菱形,
∴AB=CD,AB∥CD,
∴∠ABP=∠CDQ,
∵AP∥CQ,
∴∠APD=∠CQB,
∴∠APB=∠CQD,
在△ABP和CDQ中,
,
∴△ABP≌CDQ,
∴BP=DQ.
(2)∵∠ABC=90°,
∴菱形ABCD为正方形,
∴∠ABD=45°,∠BAD=90°,
∴在RT△ABD中,由勾股定理得:BD=BA,
由(1)得 BP=DQ,
∴BP+BQ=DQ+BQ=BD,
∴BP+BQ=BA.
(3)BP、BQ、BA之间的数量关系BQ-BP=BA,
理由如下:连接AC交BD于点H,
∵四边形ABCD是菱形,∠ABC=60°,
∴∠ABH=30°,∠AHB=90°,BD=2BH,
∴BH=AB cos∠ABH=BA,
由(1)得,BP=DQ,
∴BQ-BP=BQ-DQ=BD=BA.
16.以四边形ABCD的边AB,BC,CD,DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E,F,G,H,顺次连接这四个点,得到四边形EFGH.
(1)如图①,当四边形ABCD为正方形时,我们发现四边形EFGH也是正方形;如图②,当四边形ABCD为矩形时,请判断四边形EFGH的形状(不要求证明).
(2)如图③,当四边形ABCD为一般平行四边形时,设∠ADC=α(0°<α<90°).
①试用含α的代数式表示∠HAE;
②求证:HE=HG.
③四边形EFGH是什么四边形?并说明理由.
解:(1)解:四边形EFGH是正方形.
(2)①解:在□ABCD中,AB∥CD,所以∠BAD=180°-∠ADC=180°-α.因为△HAD和△EAB都是等腰直角三角形,所以∠HAD=∠EAB=45°.
所以∠HAE=360°-∠HAD-∠EAB-∠BAD=360°-45°-45°-(180°-α)
=90°+α.
②证明:因为△AEB和△DGC都是等腰直角三角形
所以AE=AB,DG=CD.
在□ABCD中,AB=CD,
所以AE=DG.
因为△HAD和△GDC都是等腰直角三角形
所以∠HDA=∠CDG=45°.
所以∠HDG=∠HDA+∠ADC+∠CDG=45°+α+45°=90°+α=∠HAE.
又HA=HD,
所以△HAE≌△HDG,所以HE=HG.
③解:四边形EFGH是正方形.
理由:同②,得GH=GF,FG=FE.
因为HE=HG,所以GH=GF=EF=HE.
所以四边形EFGH是菱形.
因为△HAE≌△HDG,
所以∠DHG=∠AHE.
因为∠AHD=∠AHG+∠DHG=90°,
所以∠EHG=∠AHG+∠AHE=90°.
所以四边形EFGH是正方形.
17.已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.21cnjy.com
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.2·1·c·n·j·y
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.
解:(1)①∵四边形ABCD是矩形,
∴AD∥BC,
∴∠CAD=∠ACB,∠AEF=∠CFE,
∵EF垂直平分AC,垂足为O,
∴OA=OC,
∴△AOE≌△COF,
∴OE=OF,
∴四边形AFCE为平行四边形,
又∵EF⊥AC,
∴四边形AFCE为菱形,
②设菱形的边长AF=CF=xcm,则BF=(8﹣x)cm,
在Rt△ABF中,AB=4cm,
由勾股定理得42+(8﹣x)2=x2,
解得x=5,
∴AF=5cm;
(2)①显然当P点在AF上时,Q点在CD上,此时A、C、P、Q四点不可能构成平行四边形;
同理P点在AB上时,Q点在DE或CE上,也不能构成平行四边形,
因此只有当P点在BF上、Q点在ED上时,才能构成平行四边形,
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,PC=QA,
∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,
∴PC=5t,QA=12﹣4t,
∴5t=12﹣4t,
解得,
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,秒,
②由题意得,以A、C、P、Q四点为顶点的四边形是平行四边形时,点P、Q在互相平行的对应边上,
分三种情况:
(i)如图1,当P点在AF上、Q点在CE上时,AP=CQ,即a=12﹣b,得a+b=12
(ii)如图2,当P点在BF上、Q点在DE上时,AQ=CP,即12﹣b=a,得a+b=12
(iii)如图3,当P点在AB上、Q点在CD上时,AP=CQ,即12﹣a=b,得a+b=12,
综上所述,a与b满足的数量关系式是a+b=12(ab≠0)。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
