苏教版八年级下册第11章反比例函数强化复习学案(无答案)
文档属性
| 名称 | 苏教版八年级下册第11章反比例函数强化复习学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 332.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-06 00:00:00 | ||
图片预览


文档简介
反比例函数
【学习目标】
1.了解反比例函数的概念,知道反比例函数解析式的三种形式;能够根据问题中的条件确定反比例函数的解析式.
2.理解反比例函数的图象和性质;能利用性质解题.
3.会用待定系数法求反比例函数的解析式;能综合利用一次函数与反比例函数解题.
【知识点】
1.一般地,形如(k为常数,且k≠0)的函数叫做反比例函数,反比例函数还可以表示为k= ,x= 的形式.
2.的几何意义:表示反比例函数(k≠0)图象上任意一点向坐标轴作垂线段,与坐标轴所围成 的 .
3.反比例函数的图象是 ,当k>0时,图象分布在第 象限内,且图象在每一象限内,y随x的增大而 ;当k<0时,图象分布在第 象限内,且图象在每一象限内,y随x的增大而 .
4.反比例函数(k≠0)与正比例函数的一个交点为,则它们的另一个交点为 .
【例题精讲】
考点一:反比例函数的意义
例1.已知函数是反比例函数,那么m= .
例2.若是反比例函数,则a的取值为 .
考点二:求反比例函数的解析式
例3.已知,且与成正比例,与成反比例,且当时,;当时,.求与的函数关系式.
例4.若,且是的反比例函数,是的正比例函数,当时,;当时,.那么当时,求的值.
考点三:反比例函数的图象与数形结合思想
例5.若ab>0,则一次函数y=ax+b与反比例函数y=在同一坐标系数中的大致图象是
A B C D
例6.函数和的图象如图所示,则的x取值范围是
A.x<﹣1或x>1
B.x<﹣1或0<x<1
C.﹣1<x<0或x>1
D.﹣1<x<0或0<x<1
考点四:反比例函数的性质
例7.如图,直线与双曲线交于A、B两点,则当线段AB的长度取最小值时,a的值为
A.0
B.1
C.2
D.5
例8.反比例函数在图象所在的每一象限内,函数值y随自变量x的增大而增大,则m的取值范围是
A.m<﹣3 B.m>﹣3 C.m<3 D.m>3
例9.已知点A,B是反比例函数图象上的点,若,则一定成立的是
A. B. C. D.
考点五:反比例函数的几何意义
例10.如图,点M是双曲线上一点,ME⊥y轴,MF⊥x
轴,直线交坐标轴于A、B两点,交ME于C
点,交MF于D点,则AD·BC= .
例11.如图,在直角坐标系中,平行四边形ABCD的顶点A(0,
2)、B(1,0)在x轴、y轴上,另两个顶点C、D在第一
象限内,且AD=2AB.若反比例函数(k>0)的图
像经过C,D两点,则k的值是 .
考点六:反比例函数综合
例12.如图,点A(a,1)、B(﹣1,b)都在双曲线
(x<0)上,点P、Q分别是x轴、y轴上的动点,当四
边形PABQ的周长取最小值时,PQ所在直线的解析式是
A. B.
C. D.
例13.如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,
现将此矩形向右平移,每次平移1个单位,若第1次平移
得到的矩形的边与反比例函数图象有两个交点,它们的纵
坐标之差的绝对值为0.6,则第n次(n>1)平移得到的
矩形的边与该反比例函数图象的两个交点的纵坐标之差的
绝对值为 (用含n的代数式表示).
例14.在平面直角坐标系中直线与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2),将直线平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,则平移后的直线的解析式为 .
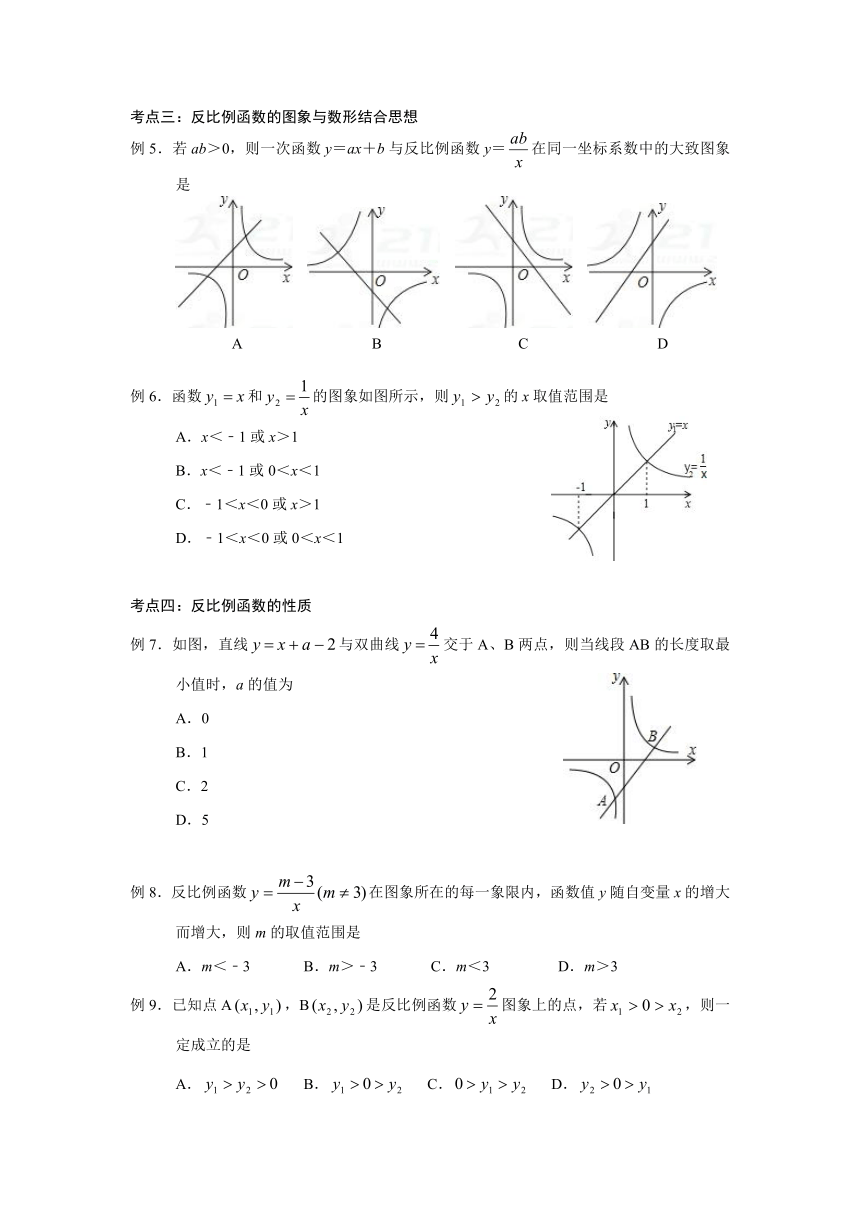
例15.如图,在平面直角坐标系中,反比例函数(x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).
(1)直接写出B、C、D三点的坐标;
(2)若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.
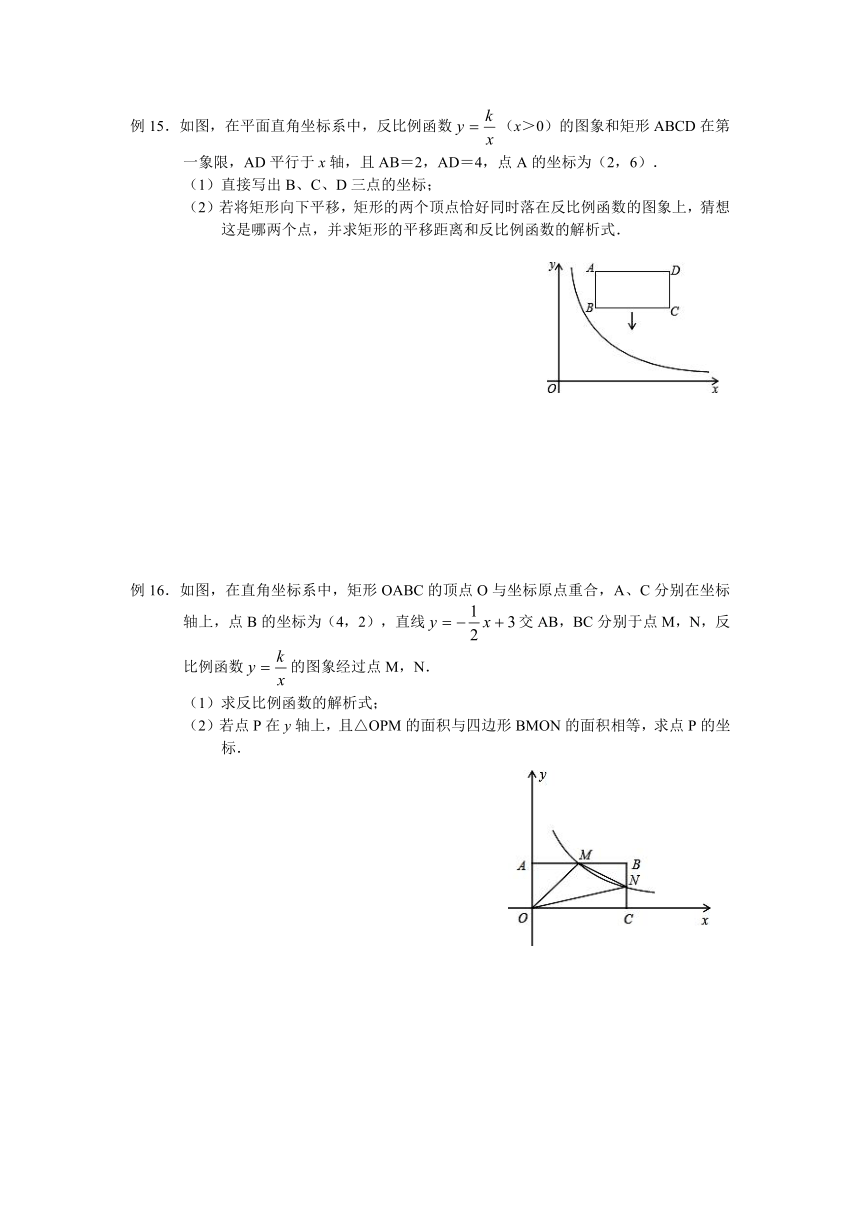
例16.如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线交AB,BC分别于点M,N,反比例函数的图象经过点M,N.
(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
考点七:反比例函数的应用
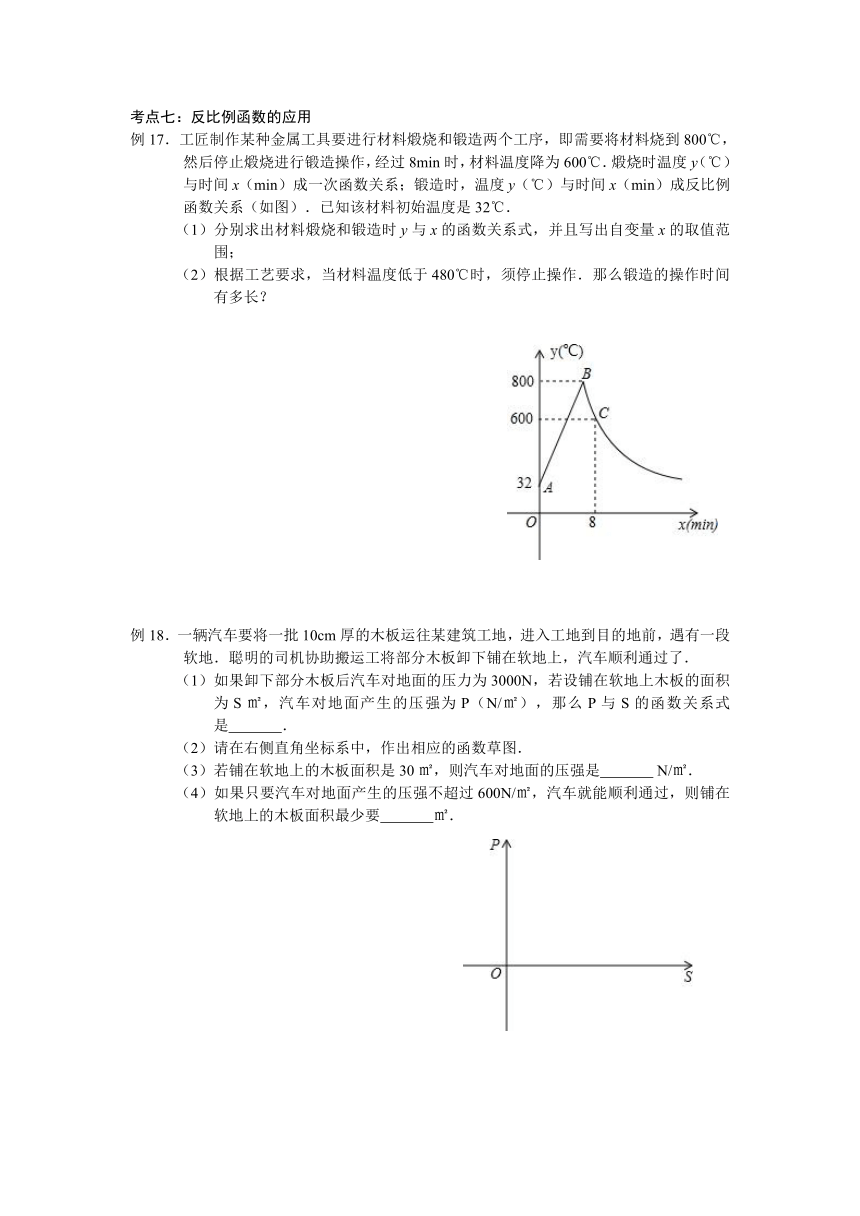
例17.工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
例18.一辆汽车要将一批10cm厚的木板运往某建筑工地,进入工地到目的地前,遇有一段软地.聪明的司机协助搬运工将部分木板卸下铺在软地上,汽车顺利通过了.
(1)如果卸下部分木板后汽车对地面的压力为3000N,若设铺在软地上木板的面积为S㎡,汽车对地面产生的压强为P(N/㎡),那么P与S的函数关系式是 .
(2)请在右侧直角坐标系中,作出相应的函数草图.
(3)若铺在软地上的木板面积是30㎡,则汽车对地面的压强是 ?N/㎡.
(4)如果只要汽车对地面产生的压强不超过600N/㎡,汽车就能顺利通过,则铺在软地上的木板面积最少要 ㎡.
【针对练习】
1.若是反比例函数,则a的取值为
A.1 B.﹣1 C.±1 D.任意实数
2.若反比例函数的图象过点(﹣2,1),则一次函数y=kx-k的图象过
A.第一、二、四象限 B.第一、三、四象限
C.第二、三、四象限 D.第一、二、三象限
3.在同一直角坐标系中,若正比例函数的图象与反比例函数的图象没有公共点,则
A. B. C. D.
4.若ab<0,则正比例函数y=ax和反比例函数在同一坐标系中的大致图象可能是
A B C D
5.如图,函数y=﹣x与函数的图象相交于A,B两点,过A,B两点分别作y轴
的垂线,垂足分别为点C,D.则四边形ACBD的面积为
A.2 B.4 C.6 D.8
6.如图,点P(a,a)是反比例函数在第一象限内的图象上的一个点,以点P为顶
点作等边△PAB,使A、B落在x轴上,则△POA的面积是
A.3 B.4 C. D.
7.如图,反比例函数(x>0)的图象经过矩形OABC对角线的交点M,分别于AB、
BC交于点D、E,若四边形ODBE的面积为9,则k的值为
A.1 B.2 C.3 D.4
第5题 第6题 第7题
8.在反比例函数的图象上有两点A(,),B(,),当<0<
时,有<,则m的取值范围是
A.m<0 B.m>0 C. D.
9.如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数的图象
经过点A,反比例函数的图象经过点B,则下列关于m,n的关系正确的是
A. B. C. D.
10.如图,直线y=x+a-2与双曲线交于A、B两点,则当线段AB的长度取最小值时,a的值为
A.0 B.1 C.2 D.5
11.如图,点A(a,1)、B(﹣1,b)都在双曲线(x<0)上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是
A. B. C. D.
第9题 第10题 第11题
12.已知正比例函数y=﹣2x与反比例函数的图象的一个交点坐标为(﹣1,2),则另一个交点的坐标为 .
13.设有反比例函数,(,),(,)为其图象上两点,若<0<,>,则k的取值范围 .
14.如果一个正比例函数的图象与反比例函数的图象交于A(,),B(,)两点,那么的值为 .
15.在平面直角坐标系xOy中,一次函数与反比例函数(x>0)的图象交点的横坐标为.若k<<k+1,则整数k的值是 .
16.如图,直线x=2与反比例函数和的图象分别交于A、B两点,若点P是y轴上任意一点,则△PAB的面积是 .
17.反比例函数(x>0)的图象如图,点B在图象上,连接OB并延长到点A,使AB=2OB,过点A作AC∥y轴,交(x>0)的图象于点C,连接OC,S△AOC=5,则k= .
18.如图,已知直线与双曲线(k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为 .
第16题 第17题 第18题
19.如图,反比例函数(x>0)的图象与矩形OABC的边长AB、BC分别交于点E、F且AE=BE,则△OEF的面积的值为 .
20.如图,在函数(x<0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC=,S△BOC=,则线段AB的长度为 .
21.如图,在函数(x>0)的图象上有点、、、…、、,点的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点、、、…、、分别作x轴、y轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分的面积从左至右依次记为、、、…、,则= ,= .(用含n的代数式表示)
第19题 第20题 第21题
22.如图①,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,sin∠A
OB=,反比例函数(k>0)在第一象限内的图象经过点A,与BC交于点F.
(1)若OA=10,求反比例函数解析式;
(2)若点F为BC的中点,且△AOF的面积S=12,求OA的长和点C的坐标;
(3)在(2)中的条件下,过点F作EF∥OB,交OA于点E(如图②),点P为直线EF上的一个动点,连接PA,PO.是否存在这样的点P,使以P、O、A为顶点的三角形是直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
23.已知:如图1,在平面直角坐标系中,O为坐标原点,直线y=kx+b与x轴、y轴分别交于点A、B,与双曲线y=相交于C、D两点,且点D的坐标为(1,6).
(1)当点C的横坐标为2时,试求直线AB的解析式,并直接写出的值.
(2)如图2,当点A落在x轴的负半轴时,过点C作x轴的垂线,垂足为E,过点D作y轴的垂线,垂足为F,连结EF.
①判断△EFC的面积和△EFD的面积是否相等,并说明理由;
②当时,求tan∠OAB的值.
图1 图2
【学习目标】
1.了解反比例函数的概念,知道反比例函数解析式的三种形式;能够根据问题中的条件确定反比例函数的解析式.
2.理解反比例函数的图象和性质;能利用性质解题.
3.会用待定系数法求反比例函数的解析式;能综合利用一次函数与反比例函数解题.
【知识点】
1.一般地,形如(k为常数,且k≠0)的函数叫做反比例函数,反比例函数还可以表示为k= ,x= 的形式.
2.的几何意义:表示反比例函数(k≠0)图象上任意一点向坐标轴作垂线段,与坐标轴所围成 的 .
3.反比例函数的图象是 ,当k>0时,图象分布在第 象限内,且图象在每一象限内,y随x的增大而 ;当k<0时,图象分布在第 象限内,且图象在每一象限内,y随x的增大而 .
4.反比例函数(k≠0)与正比例函数的一个交点为,则它们的另一个交点为 .
【例题精讲】
考点一:反比例函数的意义
例1.已知函数是反比例函数,那么m= .
例2.若是反比例函数,则a的取值为 .
考点二:求反比例函数的解析式
例3.已知,且与成正比例,与成反比例,且当时,;当时,.求与的函数关系式.
例4.若,且是的反比例函数,是的正比例函数,当时,;当时,.那么当时,求的值.
考点三:反比例函数的图象与数形结合思想
例5.若ab>0,则一次函数y=ax+b与反比例函数y=在同一坐标系数中的大致图象是
A B C D
例6.函数和的图象如图所示,则的x取值范围是
A.x<﹣1或x>1
B.x<﹣1或0<x<1
C.﹣1<x<0或x>1
D.﹣1<x<0或0<x<1
考点四:反比例函数的性质
例7.如图,直线与双曲线交于A、B两点,则当线段AB的长度取最小值时,a的值为
A.0
B.1
C.2
D.5
例8.反比例函数在图象所在的每一象限内,函数值y随自变量x的增大而增大,则m的取值范围是
A.m<﹣3 B.m>﹣3 C.m<3 D.m>3
例9.已知点A,B是反比例函数图象上的点,若,则一定成立的是
A. B. C. D.
考点五:反比例函数的几何意义
例10.如图,点M是双曲线上一点,ME⊥y轴,MF⊥x
轴,直线交坐标轴于A、B两点,交ME于C
点,交MF于D点,则AD·BC= .
例11.如图,在直角坐标系中,平行四边形ABCD的顶点A(0,
2)、B(1,0)在x轴、y轴上,另两个顶点C、D在第一
象限内,且AD=2AB.若反比例函数(k>0)的图
像经过C,D两点,则k的值是 .
考点六:反比例函数综合
例12.如图,点A(a,1)、B(﹣1,b)都在双曲线
(x<0)上,点P、Q分别是x轴、y轴上的动点,当四
边形PABQ的周长取最小值时,PQ所在直线的解析式是
A. B.
C. D.
例13.如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,
现将此矩形向右平移,每次平移1个单位,若第1次平移
得到的矩形的边与反比例函数图象有两个交点,它们的纵
坐标之差的绝对值为0.6,则第n次(n>1)平移得到的
矩形的边与该反比例函数图象的两个交点的纵坐标之差的
绝对值为 (用含n的代数式表示).
例14.在平面直角坐标系中直线与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2),将直线平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,则平移后的直线的解析式为 .
例15.如图,在平面直角坐标系中,反比例函数(x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).
(1)直接写出B、C、D三点的坐标;
(2)若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.
例16.如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线交AB,BC分别于点M,N,反比例函数的图象经过点M,N.
(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
考点七:反比例函数的应用
例17.工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
例18.一辆汽车要将一批10cm厚的木板运往某建筑工地,进入工地到目的地前,遇有一段软地.聪明的司机协助搬运工将部分木板卸下铺在软地上,汽车顺利通过了.
(1)如果卸下部分木板后汽车对地面的压力为3000N,若设铺在软地上木板的面积为S㎡,汽车对地面产生的压强为P(N/㎡),那么P与S的函数关系式是 .
(2)请在右侧直角坐标系中,作出相应的函数草图.
(3)若铺在软地上的木板面积是30㎡,则汽车对地面的压强是 ?N/㎡.
(4)如果只要汽车对地面产生的压强不超过600N/㎡,汽车就能顺利通过,则铺在软地上的木板面积最少要 ㎡.
【针对练习】
1.若是反比例函数,则a的取值为
A.1 B.﹣1 C.±1 D.任意实数
2.若反比例函数的图象过点(﹣2,1),则一次函数y=kx-k的图象过
A.第一、二、四象限 B.第一、三、四象限
C.第二、三、四象限 D.第一、二、三象限
3.在同一直角坐标系中,若正比例函数的图象与反比例函数的图象没有公共点,则
A. B. C. D.
4.若ab<0,则正比例函数y=ax和反比例函数在同一坐标系中的大致图象可能是
A B C D
5.如图,函数y=﹣x与函数的图象相交于A,B两点,过A,B两点分别作y轴
的垂线,垂足分别为点C,D.则四边形ACBD的面积为
A.2 B.4 C.6 D.8
6.如图,点P(a,a)是反比例函数在第一象限内的图象上的一个点,以点P为顶
点作等边△PAB,使A、B落在x轴上,则△POA的面积是
A.3 B.4 C. D.
7.如图,反比例函数(x>0)的图象经过矩形OABC对角线的交点M,分别于AB、
BC交于点D、E,若四边形ODBE的面积为9,则k的值为
A.1 B.2 C.3 D.4
第5题 第6题 第7题
8.在反比例函数的图象上有两点A(,),B(,),当<0<
时,有<,则m的取值范围是
A.m<0 B.m>0 C. D.
9.如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数的图象
经过点A,反比例函数的图象经过点B,则下列关于m,n的关系正确的是
A. B. C. D.
10.如图,直线y=x+a-2与双曲线交于A、B两点,则当线段AB的长度取最小值时,a的值为
A.0 B.1 C.2 D.5
11.如图,点A(a,1)、B(﹣1,b)都在双曲线(x<0)上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是
A. B. C. D.
第9题 第10题 第11题
12.已知正比例函数y=﹣2x与反比例函数的图象的一个交点坐标为(﹣1,2),则另一个交点的坐标为 .
13.设有反比例函数,(,),(,)为其图象上两点,若<0<,>,则k的取值范围 .
14.如果一个正比例函数的图象与反比例函数的图象交于A(,),B(,)两点,那么的值为 .
15.在平面直角坐标系xOy中,一次函数与反比例函数(x>0)的图象交点的横坐标为.若k<<k+1,则整数k的值是 .
16.如图,直线x=2与反比例函数和的图象分别交于A、B两点,若点P是y轴上任意一点,则△PAB的面积是 .
17.反比例函数(x>0)的图象如图,点B在图象上,连接OB并延长到点A,使AB=2OB,过点A作AC∥y轴,交(x>0)的图象于点C,连接OC,S△AOC=5,则k= .
18.如图,已知直线与双曲线(k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为 .
第16题 第17题 第18题
19.如图,反比例函数(x>0)的图象与矩形OABC的边长AB、BC分别交于点E、F且AE=BE,则△OEF的面积的值为 .
20.如图,在函数(x<0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC=,S△BOC=,则线段AB的长度为 .
21.如图,在函数(x>0)的图象上有点、、、…、、,点的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点、、、…、、分别作x轴、y轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分的面积从左至右依次记为、、、…、,则= ,= .(用含n的代数式表示)
第19题 第20题 第21题
22.如图①,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,sin∠A
OB=,反比例函数(k>0)在第一象限内的图象经过点A,与BC交于点F.
(1)若OA=10,求反比例函数解析式;
(2)若点F为BC的中点,且△AOF的面积S=12,求OA的长和点C的坐标;
(3)在(2)中的条件下,过点F作EF∥OB,交OA于点E(如图②),点P为直线EF上的一个动点,连接PA,PO.是否存在这样的点P,使以P、O、A为顶点的三角形是直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
23.已知:如图1,在平面直角坐标系中,O为坐标原点,直线y=kx+b与x轴、y轴分别交于点A、B,与双曲线y=相交于C、D两点,且点D的坐标为(1,6).
(1)当点C的横坐标为2时,试求直线AB的解析式,并直接写出的值.
(2)如图2,当点A落在x轴的负半轴时,过点C作x轴的垂线,垂足为E,过点D作y轴的垂线,垂足为F,连结EF.
①判断△EFC的面积和△EFD的面积是否相等,并说明理由;
②当时,求tan∠OAB的值.
图1 图2
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
