北师大版七年级下册 第一章 平方差公式和完全平方公式 复习和拓展 练习课件 (共38张PPT)
文档属性
| 名称 | 北师大版七年级下册 第一章 平方差公式和完全平方公式 复习和拓展 练习课件 (共38张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 435.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-08 00:00:00 | ||
图片预览











文档简介
课件38张PPT。平方差公式和完全平方公式复习和拓展平方差公式:(a+b)(a?b)=a2?b2两数和与这两数差的积,等于这两数的平方差.公式变形:1、(a – b ) ( a + b) = a2 - b22、(b + a )( -b + a ) = a2 - b2记忆口诀一同一异=同平方-异平方 1、对应练习
1.下面各式的计算对不对?如果不对,应当怎样改正?
(1)(x+3)(x-3)=x2-3; (2)(-3a-5)(3a-5)=9a2-25.2、下列多项式乘法中,能用平方差公式计算的是( ):
(1)(x+1)(1+x); (2)(a+b)(b-a) ;
(3)(-a+b)(a-b); (4)(x2-y)(x+y2);
(5)(-a-b)(a-b); (6)(c2-d2)(d2+c2). 3、利用平方差公式计算: (1)(5+6x)(5-6x); (2)(x-2y)(x+2y);
(3)(-m+n)(-m-n). √√√完全平方公式:
(a+b)2 = a2+2ab+b2
(a-b)2 = a2-2ab+b2首平方,尾平方,2倍乘积在中央。
加减看前方,同号加,异号减,
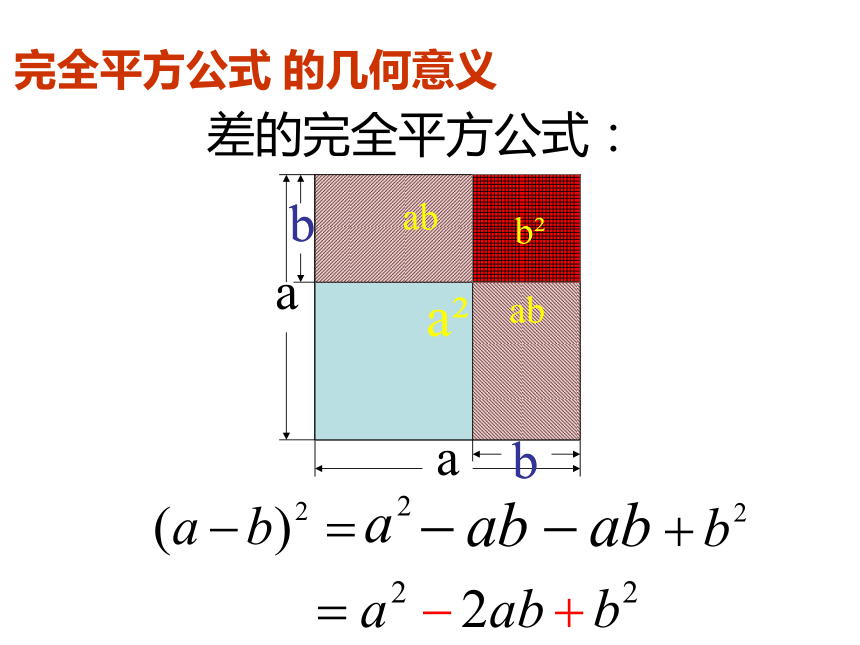
展开有三项 。 记忆口诀:(a+b)2a2b2和的完全平方公式:完全平方公式 的几何意义(a-b)2b2差的完全平方公式:完全平方公式 的几何意义1、对应练习:
(1)(2x+1)2 (2)(1-m)2
(3) (4)(2-y)2
(5)(x-4)2 (6)
(7) (2x + y)2 (8) (a -2b)2
(9)1032 2.利用公式进行计算:3.在横线上添上适当的代数式,使等式成立2ab2ab4ab4.公式变形的应用:597(a+b)2 = a2+b2+2ab
(a-b)2 = a2+b2-2ab5.完全平方式±8±20366、化简求值:(1)9x+7 -2
(2)2ab -27.小试牛刀D小试牛刀D小试牛刀D小试牛刀(2)(a+9b)(-9b+a) (1)(4y+1)(4y-1) (3)(y-x)(-x-y) (4) (m2+2)(m2- 2)
当堂检测
1、运用平方差公式计算(6)105×95 2、 运用完全平方公式计算:
(3x-2)2 (2) (-2n-5)2
(3)(5m2 +n)2 (4) 972 3、填空题:
(1)(3a-2b)(___+2b)=9a2-4b2
(2) (x-6)2=x2+_____ +36
(3)x2-4x+____=(x-____)2
3a(-12x) 424、选择题
(1)下列各式中,是完全平方公式的是( )
(A)x2-x+1 (B)4x2+1
(C)x2+2x+1 (D)x2+2x-1
(2)如y2+ay+9是完全平方公式,则a的值等于( )
(A) 3 (B)-6
(C) 6 (D)6或-6
(3)下列计算正确的是( )
A.(x-2y)(2y-x) =4y2-x2 B.(-x-1)(x+1)=x2-1
C.(m-n)(-m-n) =-m2+n2
D.(x2+2y)(x-2y)=x3-4y2cDC5、化简求值:
(a+2b)2-(a+2b)(a-2b),其中a=-2,b=知识拓展能力提高拓展与迁移
1、若不论x取何值,多项式 x3-2x2- 4x-1
与 (x+1)(x2+mx+n)都相等, 求m、n的值。2 、求使 (x2+px+8)(x2-3x+q)的积中
不含 x2与x3项 p、q的值 3、在横线上填上适当的式子,使等号两边成立。(2)(1)(3)(4)4、计算 5、已知x2-y2=8,x+y=4,求x与y的值。6、已知 (a+b)2=4, (a-b)2=6,
求(1) a2+b2 (2) ab 的值7、已知a-b=2, ab=1, 求(a+b)2的值8、已知a+b=7,ab=12,求
a2+b2 , a2-ab+b2 , (a-b)2 的值10、若x-2y=15,xy=-25,求x2+4y2-1的值。1、已知b2=ac,求证:
(a+b+c)(a-b+c)(a2-b2+c2)=a4+b4+c42、已知:若(z-x)2-4(x-y)(y-z) =0
求证: x-2y+z=0挑战自我小结回顾1、平方差公式、完全平方公式的内容是什么?2、请同学们掌握平方差、完全平方公式的结构 特征。(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b23、我们要正确理解公式中字母的广泛含义:它可以是数字、字母或其他代数式,只要符合公式的结构特征,就可以运用这一公式. (a+b)(a-b)=a2-b2
1.下面各式的计算对不对?如果不对,应当怎样改正?
(1)(x+3)(x-3)=x2-3; (2)(-3a-5)(3a-5)=9a2-25.2、下列多项式乘法中,能用平方差公式计算的是( ):
(1)(x+1)(1+x); (2)(a+b)(b-a) ;
(3)(-a+b)(a-b); (4)(x2-y)(x+y2);
(5)(-a-b)(a-b); (6)(c2-d2)(d2+c2). 3、利用平方差公式计算: (1)(5+6x)(5-6x); (2)(x-2y)(x+2y);
(3)(-m+n)(-m-n). √√√完全平方公式:
(a+b)2 = a2+2ab+b2
(a-b)2 = a2-2ab+b2首平方,尾平方,2倍乘积在中央。
加减看前方,同号加,异号减,
展开有三项 。 记忆口诀:(a+b)2a2b2和的完全平方公式:完全平方公式 的几何意义(a-b)2b2差的完全平方公式:完全平方公式 的几何意义1、对应练习:
(1)(2x+1)2 (2)(1-m)2
(3) (4)(2-y)2
(5)(x-4)2 (6)
(7) (2x + y)2 (8) (a -2b)2
(9)1032 2.利用公式进行计算:3.在横线上添上适当的代数式,使等式成立2ab2ab4ab4.公式变形的应用:597(a+b)2 = a2+b2+2ab
(a-b)2 = a2+b2-2ab5.完全平方式±8±20366、化简求值:(1)9x+7 -2
(2)2ab -27.小试牛刀D小试牛刀D小试牛刀D小试牛刀(2)(a+9b)(-9b+a) (1)(4y+1)(4y-1) (3)(y-x)(-x-y) (4) (m2+2)(m2- 2)
当堂检测
1、运用平方差公式计算(6)105×95 2、 运用完全平方公式计算:
(3x-2)2 (2) (-2n-5)2
(3)(5m2 +n)2 (4) 972 3、填空题:
(1)(3a-2b)(___+2b)=9a2-4b2
(2) (x-6)2=x2+_____ +36
(3)x2-4x+____=(x-____)2
3a(-12x) 424、选择题
(1)下列各式中,是完全平方公式的是( )
(A)x2-x+1 (B)4x2+1
(C)x2+2x+1 (D)x2+2x-1
(2)如y2+ay+9是完全平方公式,则a的值等于( )
(A) 3 (B)-6
(C) 6 (D)6或-6
(3)下列计算正确的是( )
A.(x-2y)(2y-x) =4y2-x2 B.(-x-1)(x+1)=x2-1
C.(m-n)(-m-n) =-m2+n2
D.(x2+2y)(x-2y)=x3-4y2cDC5、化简求值:
(a+2b)2-(a+2b)(a-2b),其中a=-2,b=知识拓展能力提高拓展与迁移
1、若不论x取何值,多项式 x3-2x2- 4x-1
与 (x+1)(x2+mx+n)都相等, 求m、n的值。2 、求使 (x2+px+8)(x2-3x+q)的积中
不含 x2与x3项 p、q的值 3、在横线上填上适当的式子,使等号两边成立。(2)(1)(3)(4)4、计算 5、已知x2-y2=8,x+y=4,求x与y的值。6、已知 (a+b)2=4, (a-b)2=6,
求(1) a2+b2 (2) ab 的值7、已知a-b=2, ab=1, 求(a+b)2的值8、已知a+b=7,ab=12,求
a2+b2 , a2-ab+b2 , (a-b)2 的值10、若x-2y=15,xy=-25,求x2+4y2-1的值。1、已知b2=ac,求证:
(a+b+c)(a-b+c)(a2-b2+c2)=a4+b4+c42、已知:若(z-x)2-4(x-y)(y-z) =0
求证: x-2y+z=0挑战自我小结回顾1、平方差公式、完全平方公式的内容是什么?2、请同学们掌握平方差、完全平方公式的结构 特征。(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b23、我们要正确理解公式中字母的广泛含义:它可以是数字、字母或其他代数式,只要符合公式的结构特征,就可以运用这一公式. (a+b)(a-b)=a2-b2
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
