2017-2018学年苏科版八年级数学下册 第九章 反比例函数的图像与性质 提高卷
文档属性
| 名称 | 2017-2018学年苏科版八年级数学下册 第九章 反比例函数的图像与性质 提高卷 |
|
|
| 格式 | zip | ||
| 文件大小 | 299.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-09 00:00:00 | ||
图片预览


文档简介
反比例函数的图像与性质
一、选择题
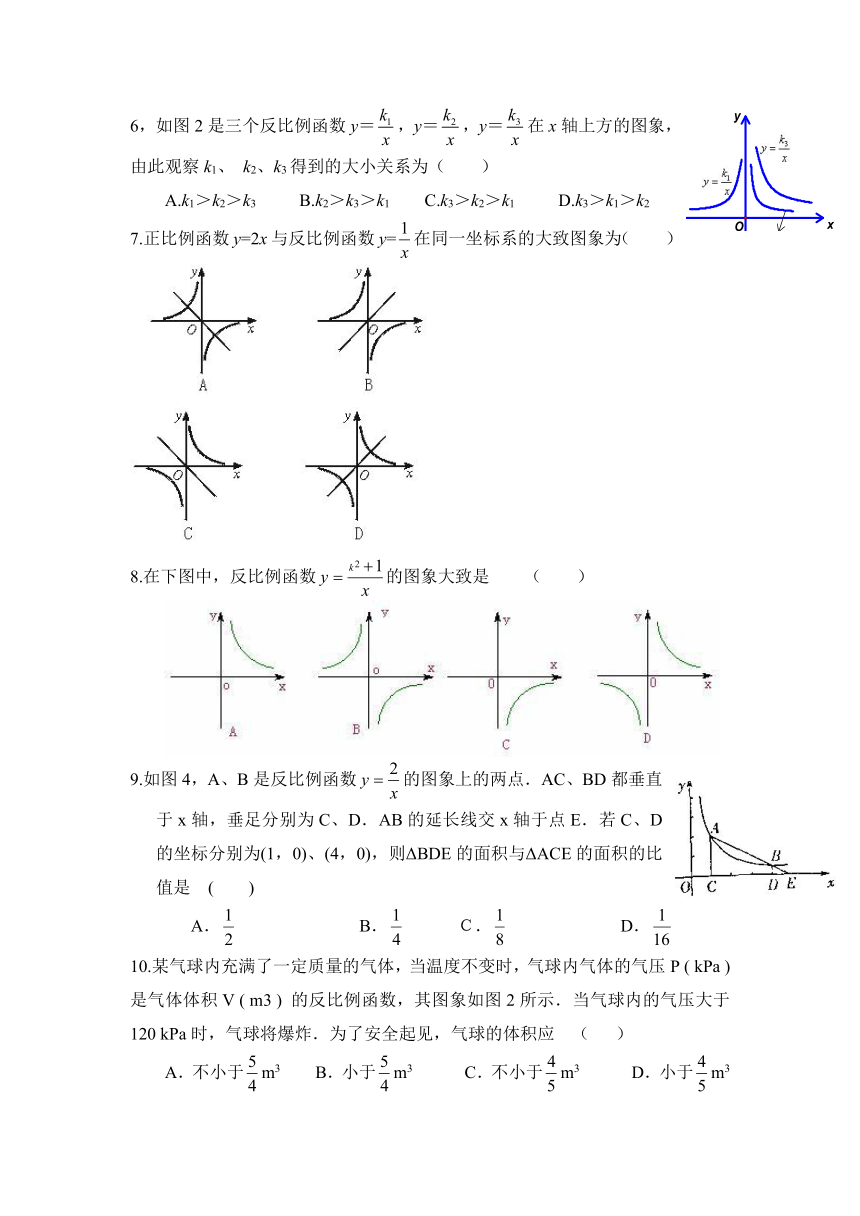
1.若ab<0,则正比例函数y=ax和反比例函数y=在同一坐标系中的大致图像可能是 ( )
2.一次函数与反比例函数,在同一直角坐标系中的图象如图所示,若,则x的取值范围是
A. 或 B. C. 或 D.
3.已知反比例函数的图象上两点A(x1,y1),B(x2,y2),当x1<0<x2时,有y1<y2,则m的取值范围是 ( )
A. m>0 B. m> C. m<0 D. m<
4.如图是反比例函数y=(k为常数,k≠0)的图象,则一次函数y=kx﹣k的图象大致是( )
A. B. C. D.
5.当a≠0时,函数y=ax+1与函数y=在同一坐标系中的图象可能是( )
A. B. C. D.
6,如图2是三个反比例函数y=,y=,y=在x轴上方的图象,由此观察k1、 k2、k3得到的大小关系为( )
A.k1>k2>k3 B.k2>k3>k1 C.k3>k2>k1 D.k3>k1>k2
7.正比例函数y=2x与反比例函数y=在同一坐标系的大致图象为( )
8.在下图中,反比例函数的图象大致是 ( )
9.如图4,A、B是反比例函数的图象上的两点.AC、BD都垂直于x轴,垂足分别为C、D.AB的延长线交x轴于点E.若C、D的坐标分别为(1,0)、(4,0),则ΔBDE的面积与ΔACE的面积的比值是 ( )
A. B. C. D.
10.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3 ) 的反比例函数,其图象如图2所示.当气球内的气压大于120 kPa时,气球将爆炸.为了安全起见,气球的体积应 ( )
A.不小于m3 B.小于m3 C.不小于m3 D.小于m3
二、填空题
11.已知双曲线y=经过点(-1,2),那么k的值等于_______.
12.如图,已知点A在反比例函数图像上,AM⊥x轴于点M,且△AOM的面积为1,则反比例函数的解析式为_______.
13.设反比例函数y=,(x1,y1),(x2,y2)为其图像上两点,若x1<0y2,则k的取值范围是_______.
14.如图,点M是反比例函数()图象上任意一点,AB⊥y轴于B,点C是x轴上的动点,则△ABC的面积为______
15.已知函数y=(m2﹣1),当m= 时,它的图象是双曲线.
16.若反比例函数y=(2k﹣1)的图象位于二、四象限,则k= .
17.如图,点P是正比例函数y=x与反比例函数y=在第一象限内的交点,PA⊥OP交x轴于点A,△POA的面积为2,则k的值是 .
18.如图,一次函数y1=ax+b(a≠0)与反比例函数的图象交于A(1,4)、B(4,1)两点,若使y1>y2,则x的取值范围是 .
19.已知反比例函数y=(k≠0),当x>0时,y随x的增大而增大,那么一次函数y=kx-k的图像过 象限.
20.函数y= (k>0)的图象上两点A(x1, y1)和B(x2, y2),且x1>x2>0,分别过A、
B向x轴作AA1⊥x轴于A1,BB1⊥x轴于B1,则_________ (填“>”“=”
或“<”),若=2,则函数解析式为_________.
三、解答题
21.已知反比例函数的图象经过. 求k的值. 这个函数的图象在哪几个象限?y随x的增大怎样变化? 画出函数的图象. 点在这个函数的图象上吗?
22.如图,直线y=k1x+b与双曲线y=相交于A(1,2)、B(m,-1)两点.
(1)求直线和双曲线的解析式;
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且 x1(3)观察图像,请直接写出不等式k1x+b>的解集.
23.如图,正方形OABC的面积为9,点O为左边原点,点A在轴上,点C在轴上,点B在函数的图象上,点P是函数图象上的任意一点,过点P分别作轴、轴的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合的部分(图中阴影部分)的面积为S.
(1)求B点坐标和值;
(2)当时,求P点坐标.
24.已知:如图,反比例函数y=的图象与一次函数y=x+b的图象交于点A(1,4)、点B(﹣4,n).
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
25.如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况。实验数据记录如下:
x(cm)
…
10
15
20
25
30
…
y(N)
…
30
20
15
12
10
…
(1)把上表中x,y的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点并观察所得的图象,猜测y(N)与x(cm)
之间的函数关系,并求出函数关系式;
(2)当弹簧秤的示数为24N时,弹簧秤与O点的距离是多少cm?随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将发生怎样的变化?
答案
1.C 2. C 3.D 4.B 5.C 6,C. 7.D 8.D 9.D10.C
11.-3 12.y=- 13.k<-2 14.1 15.0 16.0 17.2
18.x<0或121. 解:反比例函数的图象经过点,
;
解得:;
,
图象位于二、四象限,在每个象限内y随x的增大而增大;
图象为:
、
,
在反比例函数的图象上,不在反比例函数的图象上.??
22.(1)双曲线的解析式为:y= 直线的解析式为:y=x+1; (2)y21或-223.解:(1)设B(),则,
且,故B点坐标为(3,3).又因为B点坐标为(3,3)
在的图象上,所以,
所以双曲线关系式为.
(2)设AB与PF交于点H,因为P()在上,
所以,,
所以,.当时,,
所以.所以P点坐标为.
当P点在B点上方时,同理求得.
故当时,P点坐标为或.
24.解:(1)把A点(1,4)分别代入反比例函数y=,一次函数y=x+b,得k=1×4,1+b=4,
解得k=4,b=3,
∴反比例函数的解析式是y=,一次函数解析式是y=x+3;
(2)如图,设直线y=x+3与y轴的交点为C,
当x=﹣4时,y=﹣1,
∴B(﹣4,﹣1),
当x=0时,y=+3,
∴C(0,3),
∴S△AOB=S△AOC+S△BOC==;
(3)∵B(﹣4,﹣1),A(1,4),
∴根据图象可知:当x>1或﹣4<x<0时,一次函数值大于反比例函数值.
25、解:(1)如图,猜测y是x的反比例函数,
设y=,把x=10, y=30代入,
得k=30, 所以 y=(x>0)。
(2)y=,当y=24时,解得x=12.5。
随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将不断增大。
一、选择题
1.若ab<0,则正比例函数y=ax和反比例函数y=在同一坐标系中的大致图像可能是 ( )
2.一次函数与反比例函数,在同一直角坐标系中的图象如图所示,若,则x的取值范围是
A. 或 B. C. 或 D.
3.已知反比例函数的图象上两点A(x1,y1),B(x2,y2),当x1<0<x2时,有y1<y2,则m的取值范围是 ( )
A. m>0 B. m> C. m<0 D. m<
4.如图是反比例函数y=(k为常数,k≠0)的图象,则一次函数y=kx﹣k的图象大致是( )
A. B. C. D.
5.当a≠0时,函数y=ax+1与函数y=在同一坐标系中的图象可能是( )
A. B. C. D.
6,如图2是三个反比例函数y=,y=,y=在x轴上方的图象,由此观察k1、 k2、k3得到的大小关系为( )
A.k1>k2>k3 B.k2>k3>k1 C.k3>k2>k1 D.k3>k1>k2
7.正比例函数y=2x与反比例函数y=在同一坐标系的大致图象为( )
8.在下图中,反比例函数的图象大致是 ( )
9.如图4,A、B是反比例函数的图象上的两点.AC、BD都垂直于x轴,垂足分别为C、D.AB的延长线交x轴于点E.若C、D的坐标分别为(1,0)、(4,0),则ΔBDE的面积与ΔACE的面积的比值是 ( )
A. B. C. D.
10.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3 ) 的反比例函数,其图象如图2所示.当气球内的气压大于120 kPa时,气球将爆炸.为了安全起见,气球的体积应 ( )
A.不小于m3 B.小于m3 C.不小于m3 D.小于m3
二、填空题
11.已知双曲线y=经过点(-1,2),那么k的值等于_______.
12.如图,已知点A在反比例函数图像上,AM⊥x轴于点M,且△AOM的面积为1,则反比例函数的解析式为_______.
13.设反比例函数y=,(x1,y1),(x2,y2)为其图像上两点,若x1<0
14.如图,点M是反比例函数()图象上任意一点,AB⊥y轴于B,点C是x轴上的动点,则△ABC的面积为______
15.已知函数y=(m2﹣1),当m= 时,它的图象是双曲线.
16.若反比例函数y=(2k﹣1)的图象位于二、四象限,则k= .
17.如图,点P是正比例函数y=x与反比例函数y=在第一象限内的交点,PA⊥OP交x轴于点A,△POA的面积为2,则k的值是 .
18.如图,一次函数y1=ax+b(a≠0)与反比例函数的图象交于A(1,4)、B(4,1)两点,若使y1>y2,则x的取值范围是 .
19.已知反比例函数y=(k≠0),当x>0时,y随x的增大而增大,那么一次函数y=kx-k的图像过 象限.
20.函数y= (k>0)的图象上两点A(x1, y1)和B(x2, y2),且x1>x2>0,分别过A、
B向x轴作AA1⊥x轴于A1,BB1⊥x轴于B1,则_________ (填“>”“=”
或“<”),若=2,则函数解析式为_________.
三、解答题
21.已知反比例函数的图象经过. 求k的值. 这个函数的图象在哪几个象限?y随x的增大怎样变化? 画出函数的图象. 点在这个函数的图象上吗?
22.如图,直线y=k1x+b与双曲线y=相交于A(1,2)、B(m,-1)两点.
(1)求直线和双曲线的解析式;
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且 x1
23.如图,正方形OABC的面积为9,点O为左边原点,点A在轴上,点C在轴上,点B在函数的图象上,点P是函数图象上的任意一点,过点P分别作轴、轴的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合的部分(图中阴影部分)的面积为S.
(1)求B点坐标和值;
(2)当时,求P点坐标.
24.已知:如图,反比例函数y=的图象与一次函数y=x+b的图象交于点A(1,4)、点B(﹣4,n).
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
25.如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况。实验数据记录如下:
x(cm)
…
10
15
20
25
30
…
y(N)
…
30
20
15
12
10
…
(1)把上表中x,y的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点并观察所得的图象,猜测y(N)与x(cm)
之间的函数关系,并求出函数关系式;
(2)当弹簧秤的示数为24N时,弹簧秤与O点的距离是多少cm?随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将发生怎样的变化?
答案
1.C 2. C 3.D 4.B 5.C 6,C. 7.D 8.D 9.D10.C
11.-3 12.y=- 13.k<-2 14.1 15.0 16.0 17.2
18.x<0或1
22.(1)双曲线的解析式为:y= 直线的解析式为:y=x+1; (2)y2
且,故B点坐标为(3,3).又因为B点坐标为(3,3)
在的图象上,所以,
所以双曲线关系式为.
(2)设AB与PF交于点H,因为P()在上,
所以,,
所以,.当时,,
所以.所以P点坐标为.
当P点在B点上方时,同理求得.
故当时,P点坐标为或.
24.解:(1)把A点(1,4)分别代入反比例函数y=,一次函数y=x+b,得k=1×4,1+b=4,
解得k=4,b=3,
∴反比例函数的解析式是y=,一次函数解析式是y=x+3;
(2)如图,设直线y=x+3与y轴的交点为C,
当x=﹣4时,y=﹣1,
∴B(﹣4,﹣1),
当x=0时,y=+3,
∴C(0,3),
∴S△AOB=S△AOC+S△BOC==;
(3)∵B(﹣4,﹣1),A(1,4),
∴根据图象可知:当x>1或﹣4<x<0时,一次函数值大于反比例函数值.
25、解:(1)如图,猜测y是x的反比例函数,
设y=,把x=10, y=30代入,
得k=30, 所以 y=(x>0)。
(2)y=,当y=24时,解得x=12.5。
随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将不断增大。
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
