2018年高考物理三轮复习每日一题2018年4月12日+碰撞与动量守恒(二)
文档属性
| 名称 | 2018年高考物理三轮复习每日一题2018年4月12日+碰撞与动量守恒(二) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2018-04-11 08:54:26 | ||
图片预览



文档简介
4月12日 碰撞与动量守恒(二)
高考频度:★★★☆☆
难易程度:★★★☆☆
装甲车和战舰采用多层钢板比采用同样质量的单层钢板更能抵御穿甲弹的射击。通过对以下简化模型的计算可以粗略说明其原因。质量为2m、厚度为2d的钢板静止在水平光滑桌面上。质量为m的子弹以某一速度垂直射向该钢板,刚好能将钢板射穿。现把钢板分成厚度均为d、质量均为m的相同两块,间隔一段距离水平放置,如图所示。若子弹以相同的速度垂直射向第一块钢板,穿出后再射向第二块钢板,求子弹射入第二块钢板的深度。设子弹在钢板中受到的阻力为恒力,且两块钢板不会发生碰撞。不计重力影响。
(1)子弹射穿质量为2m、厚度为2d的钢板后钢板的速度和此过程系统损失的机械能;
(2)子弹射穿质量为m、厚度为d的第一块钢板后的速度;
(3)子弹射入第二块钢板的深度。
【参考答案】(1) (2) (3)
【试题解析】(1)设子弹初速度为v0,射入厚度为2d的钢板后,最终钢板和子弹的共同速度为v。由动量守恒得 ①
解得
此过程中动能的损失为 ②
解得
(2)分成两块钢板后,设子弹穿过第一块钢板时子弹和钢板的速度为别为v1和v2,由动量守恒得
③
根据能量守恒得: ④
联立①②③④解得:
(3)子弹以速度垂直射向第二块钢板在第二块钢板中进入深度,公共速度,则由系统动量守恒和摩擦力做功等于系统动能的减少,有: ⑤
⑥
联立以上各式化简得:
【知识补给】
木块置于光滑水平面上
子弹和木块构成系统不受外力作用,系统动量守恒,系统内力是一对相互作用的摩擦力,子弹受到的摩擦力做负功,木块受到的摩擦力做正功。如图所示,设子弹质量为m,水平初速度为v0,置于光滑水平面上的木块质量为M。若子弹未穿过木块,则子弹和木块最终共速为v。
由动量守恒定律: ①
对于子弹,由动能定理:②
对于木块,由动能定理:③
由①②③可得:④
系统动能的减少量转化为系统内能Q
(1)若时,说明子弹刚好穿过木块,子弹和木块具有共同速度v。
(2)若时,说明子弹未能穿过木块,最终子弹留在木块中,子弹和木块具有共同速度v。
(3)当时,说明子弹能穿过木块,子弹射穿木块时的速度大于木块的速度。
若属于(3)的情况,设穿透后子弹和木块的速度分别为v1和v2,上述关系式变为:
⑤
⑥
⑦
⑧
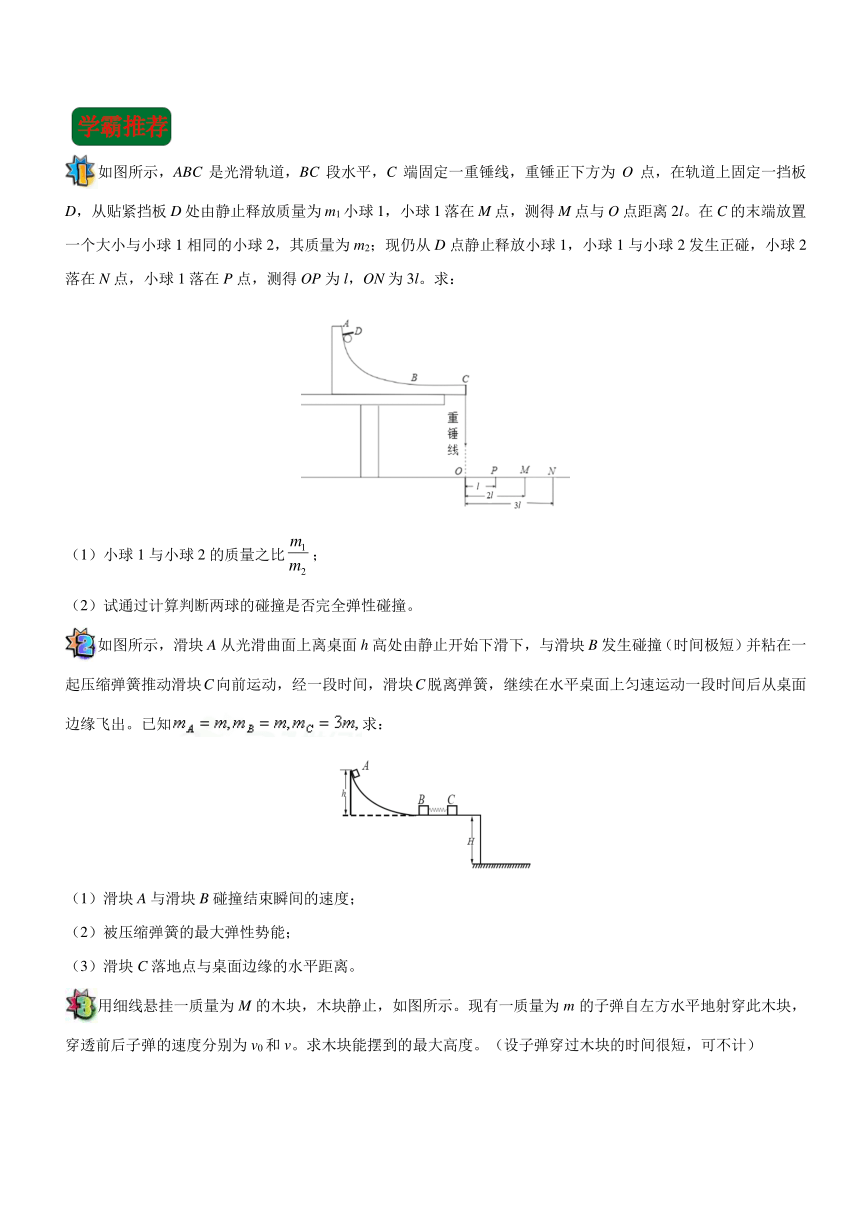
如图所示,ABC是光滑轨道,BC段水平,C端固定一重锤线,重锤正下方为O点,在轨道上固定一挡板D,从贴紧挡板D处由静止释放质量为m1小球1,小球1落在M点,测得M点与O点距离2l。在C的末端放置一个大小与小球1相同的小球2,其质量为m2;现仍从D点静止释放小球1,小球1与小球2发生正碰,小球2落在N点,小球1落在P点,测得OP为l,ON为3l。求:
(1)小球1与小球2的质量之比;
(2)试通过计算判断两球的碰撞是否完全弹性碰撞。
如图所示,滑块A从光滑曲面上离桌面h高处由静止开始下滑下,与滑块B发生碰撞(时间极短)并粘在一起压缩弹簧推动滑块C向前运动,经一段时间,滑块C脱离弹簧,继续在水平桌面上匀速运动一段时间后从桌面边缘飞出。已知求:
(1)滑块A与滑块B碰撞结束瞬间的速度;
(2)被压缩弹簧的最大弹性势能;
(3)滑块C落地点与桌面边缘的水平距离。
用细线悬挂一质量为M的木块,木块静止,如图所示。现有一质量为m的子弹自左方水平地射穿此木块,穿透前后子弹的速度分别为v0和v。求木块能摆到的最大高度。(设子弹穿过木块的时间很短,可不计)
如图,光滑冰面上静止放置一表面光滑的斜面体,斜面体右侧一蹲在滑板上的小孩和其面前的冰块均静止于冰面上。某时刻小孩将冰块以相对冰面3 m/s的速度向斜面体推出,冰块平滑地滑上斜面体,在斜面体上上升的最大高度为h=0.3 m(h小于斜面体的高度)。已知小孩与滑板的总质量为m1=30 kg,冰块的质量为m2=10 kg,小孩与滑板始终无相对运动。取重力加速度的大小g=10 m/s2。
(1)求斜面体的质量;
(2)通过计算判断,冰块与斜面体分离后能否追上小孩?
如图,在足够长的光滑水平面上,物体A、B、C位于同一直线上,A位于B、C之间。A的质量为,B、C的质量都为,三者都处于静止状态,现使A以某一速度向右运动,求和之间满足什么条件才能使A只与B、C各发生一次碰撞。设物体间的碰撞都是弹性的。
【参考答案】
,碰撞前后系统动量守恒
以球1和球2为系统,根据动量守恒定律公式③
碰后两均在空中做平抛运动
球1水平方向④
球2水平方向⑤
由①②③④⑤式联立得⑥
(2)以两球为系统,碰前系统初动能⑦
碰后系统末动能:⑧
由②③④⑤⑥⑦⑧式联立得:
则两球碰撞是弹性碰撞
解得:
(2)滑块A、B发生碰撞后与滑块C一起压缩弹簧,压缩的过程机械能守恒,被压缩弹簧的弹性势能最大时,滑块A、B、C速度相等,设为速度v3,由动量定恒定律有:
由机械能定恒定律有:
(3)被压缩的弹簧再次恢复自然长度时,滑块C脱离弹簧,设滑块A、B速度为v4,滑块C的速度为v5,分别由动量定恒定律和机械能定恒定律有:
解之得:(另一组解舍去)
滑块C从桌面边缘飞出后做平抛运动:
解得之:
由子弹和木块组成的系统在水平方向上不受外力,满足动量守恒,即mv0=mv+Mv′
v′=(v0-v)
木块以速度v′摆起过程中,只有重力做功,机械能守恒,即Mv′2=Mghm
hm=
所以hm=
解得v1=1 m/s
设冰块与斜面体分离后的速度分别为v2和v3,由水平方向动量守恒和机械能守恒有
m2v20= m2v2+ m3v3,
解得v2=1 m/s=v1,故冰块与斜面体分离后不能追上小孩
设A运动的初速度为
A向右运动与C发生碰撞,根据弹性碰撞可得
可得
要使得A与B发生碰撞,需要满足,即
A反向向左运动与B发生碰撞过程,弹性碰撞
整理可得
解方程可得
高考频度:★★★☆☆
难易程度:★★★☆☆
装甲车和战舰采用多层钢板比采用同样质量的单层钢板更能抵御穿甲弹的射击。通过对以下简化模型的计算可以粗略说明其原因。质量为2m、厚度为2d的钢板静止在水平光滑桌面上。质量为m的子弹以某一速度垂直射向该钢板,刚好能将钢板射穿。现把钢板分成厚度均为d、质量均为m的相同两块,间隔一段距离水平放置,如图所示。若子弹以相同的速度垂直射向第一块钢板,穿出后再射向第二块钢板,求子弹射入第二块钢板的深度。设子弹在钢板中受到的阻力为恒力,且两块钢板不会发生碰撞。不计重力影响。
(1)子弹射穿质量为2m、厚度为2d的钢板后钢板的速度和此过程系统损失的机械能;
(2)子弹射穿质量为m、厚度为d的第一块钢板后的速度;
(3)子弹射入第二块钢板的深度。
【参考答案】(1) (2) (3)
【试题解析】(1)设子弹初速度为v0,射入厚度为2d的钢板后,最终钢板和子弹的共同速度为v。由动量守恒得 ①
解得
此过程中动能的损失为 ②
解得
(2)分成两块钢板后,设子弹穿过第一块钢板时子弹和钢板的速度为别为v1和v2,由动量守恒得
③
根据能量守恒得: ④
联立①②③④解得:
(3)子弹以速度垂直射向第二块钢板在第二块钢板中进入深度,公共速度,则由系统动量守恒和摩擦力做功等于系统动能的减少,有: ⑤
⑥
联立以上各式化简得:
【知识补给】
木块置于光滑水平面上
子弹和木块构成系统不受外力作用,系统动量守恒,系统内力是一对相互作用的摩擦力,子弹受到的摩擦力做负功,木块受到的摩擦力做正功。如图所示,设子弹质量为m,水平初速度为v0,置于光滑水平面上的木块质量为M。若子弹未穿过木块,则子弹和木块最终共速为v。
由动量守恒定律: ①
对于子弹,由动能定理:②
对于木块,由动能定理:③
由①②③可得:④
系统动能的减少量转化为系统内能Q
(1)若时,说明子弹刚好穿过木块,子弹和木块具有共同速度v。
(2)若时,说明子弹未能穿过木块,最终子弹留在木块中,子弹和木块具有共同速度v。
(3)当时,说明子弹能穿过木块,子弹射穿木块时的速度大于木块的速度。
若属于(3)的情况,设穿透后子弹和木块的速度分别为v1和v2,上述关系式变为:
⑤
⑥
⑦
⑧
如图所示,ABC是光滑轨道,BC段水平,C端固定一重锤线,重锤正下方为O点,在轨道上固定一挡板D,从贴紧挡板D处由静止释放质量为m1小球1,小球1落在M点,测得M点与O点距离2l。在C的末端放置一个大小与小球1相同的小球2,其质量为m2;现仍从D点静止释放小球1,小球1与小球2发生正碰,小球2落在N点,小球1落在P点,测得OP为l,ON为3l。求:
(1)小球1与小球2的质量之比;
(2)试通过计算判断两球的碰撞是否完全弹性碰撞。
如图所示,滑块A从光滑曲面上离桌面h高处由静止开始下滑下,与滑块B发生碰撞(时间极短)并粘在一起压缩弹簧推动滑块C向前运动,经一段时间,滑块C脱离弹簧,继续在水平桌面上匀速运动一段时间后从桌面边缘飞出。已知求:
(1)滑块A与滑块B碰撞结束瞬间的速度;
(2)被压缩弹簧的最大弹性势能;
(3)滑块C落地点与桌面边缘的水平距离。
用细线悬挂一质量为M的木块,木块静止,如图所示。现有一质量为m的子弹自左方水平地射穿此木块,穿透前后子弹的速度分别为v0和v。求木块能摆到的最大高度。(设子弹穿过木块的时间很短,可不计)
如图,光滑冰面上静止放置一表面光滑的斜面体,斜面体右侧一蹲在滑板上的小孩和其面前的冰块均静止于冰面上。某时刻小孩将冰块以相对冰面3 m/s的速度向斜面体推出,冰块平滑地滑上斜面体,在斜面体上上升的最大高度为h=0.3 m(h小于斜面体的高度)。已知小孩与滑板的总质量为m1=30 kg,冰块的质量为m2=10 kg,小孩与滑板始终无相对运动。取重力加速度的大小g=10 m/s2。
(1)求斜面体的质量;
(2)通过计算判断,冰块与斜面体分离后能否追上小孩?
如图,在足够长的光滑水平面上,物体A、B、C位于同一直线上,A位于B、C之间。A的质量为,B、C的质量都为,三者都处于静止状态,现使A以某一速度向右运动,求和之间满足什么条件才能使A只与B、C各发生一次碰撞。设物体间的碰撞都是弹性的。
【参考答案】
,碰撞前后系统动量守恒
以球1和球2为系统,根据动量守恒定律公式③
碰后两均在空中做平抛运动
球1水平方向④
球2水平方向⑤
由①②③④⑤式联立得⑥
(2)以两球为系统,碰前系统初动能⑦
碰后系统末动能:⑧
由②③④⑤⑥⑦⑧式联立得:
则两球碰撞是弹性碰撞
解得:
(2)滑块A、B发生碰撞后与滑块C一起压缩弹簧,压缩的过程机械能守恒,被压缩弹簧的弹性势能最大时,滑块A、B、C速度相等,设为速度v3,由动量定恒定律有:
由机械能定恒定律有:
(3)被压缩的弹簧再次恢复自然长度时,滑块C脱离弹簧,设滑块A、B速度为v4,滑块C的速度为v5,分别由动量定恒定律和机械能定恒定律有:
解之得:(另一组解舍去)
滑块C从桌面边缘飞出后做平抛运动:
解得之:
由子弹和木块组成的系统在水平方向上不受外力,满足动量守恒,即mv0=mv+Mv′
v′=(v0-v)
木块以速度v′摆起过程中,只有重力做功,机械能守恒,即Mv′2=Mghm
hm=
所以hm=
解得v1=1 m/s
设冰块与斜面体分离后的速度分别为v2和v3,由水平方向动量守恒和机械能守恒有
m2v20= m2v2+ m3v3,
解得v2=1 m/s=v1,故冰块与斜面体分离后不能追上小孩
设A运动的初速度为
A向右运动与C发生碰撞,根据弹性碰撞可得
可得
要使得A与B发生碰撞,需要满足,即
A反向向左运动与B发生碰撞过程,弹性碰撞
整理可得
解方程可得
同课章节目录
