人教版高中数学课件:必修四 1.1任意角 (共41张PPT)
文档属性
| 名称 | 人教版高中数学课件:必修四 1.1任意角 (共41张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-12 09:13:30 | ||
图片预览











文档简介
课件38张PPT。由于月球和太阳的引潮力作用,使水面发生周期性涨落的潮汐现象。
???????????????????????????????????????????????????????????????????????????????????????????????????????????? 钱塘江一线潮伦敦之眼各种电波 现实世界中的很多运动,变化都有着循环往复、周而复始的现象。如何用数学的方法来刻画这种变化规律呢?
本章要学习的三角函数就是刻画这种变化规律的数学模型。必修四 第1章 三角函数
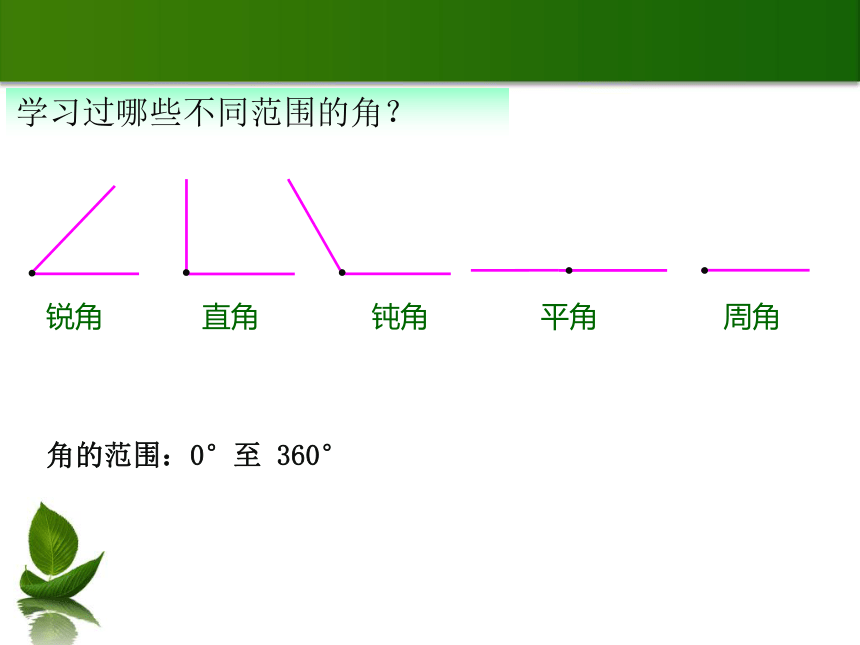
第1节 任意角学习过哪些不同范围的角?角的范围:0°至 360°体操中有转体两周半或转体三周,如何度量这些角度呢?新课2. 角的分类:1. 任意角的定义:3. 象限角与轴线角:4. 终边相同的角的表示法:一条射线绕端点从一个位置旋转到另一个位置所形成的图形.终边落在第几象限就是第几象限角.终边落在坐标轴上的角叫轴线角.正角、零角、负角.本课提纲:(阅读课本 P5-6完成下列问题)例题分析例1、在0°到360°范围内,找出与-950°12'角终边相同的角,并判定它是第几象限角;解:-950°12'=-1080°+129°48' =-3×360°+129°48'所以,-950°12'是第二象限的角因为129°48'是第二象限的角例2、写出终边在y轴上的角的集合.解:在0°~360°范围内,终边在y轴上的角有两
个,即90°,270°角(如图).
因此,所有与90°角终边相同的角构成集合
S1={β|β=90°+k·360°.k∈Z}.
而所有与270°角终边相同的角构成集合
S2={β|β=270°+k·360°.k∈Z}.例题分析于是,终边在y轴上的角的集合
S=S1∪S2
={β|β=90°+2k·180°,k∈Z }∪{β|β=90°+180°+2k·180°,k∈Z }
={β|β=90°+2k·180°,k∈Z } ∪{β|β=90°+(2k+1)180°,k∈Z }
={β|β=90°+n·180°,n∈Z }例题分析={β|β=90°+k·360°,k∈Z}∪{β|β=270°+k·360°,k∈Z} 思考1:终边在x轴正半轴、负半轴,y轴正半轴、负半轴、 x轴、y轴、坐标轴上的角分别如何表示? x轴正半轴:α= k·360°,k∈Z ;
x轴负半轴:α= 180°+k·360°,k∈Z ;
y轴正半轴:α= 90°+k·360°,k∈Z ;
y轴负半轴:α= 270°+k·360°,k∈Z ;
x轴:α= k·180°,k∈Z ;
y轴:α= 90°+k·180°,k∈Z ;
坐标轴:α= k·90°,k∈Z . 思考2:终边在直线y=x上的角分别如何表示? α= 45°+k·180°,k∈ZXYO第一象限的角表示为
第二象限的角表示为
第三象限的角表示为
第四象限的角表示为{?|k?360?旋转游戏1.初始时面朝的方向相同吗?2.终止时面朝的方向怎样?3.旋转的圈数不同有没有区别?从旋转的角度描述一下怎样可以得到一个角?一个确定的旋转应该包括哪些方面?从哪转的?转多少?怎样转的?角——有公共端点的两条射线所围成
的图形一、任意角的概念新的定义:平面内一条射线绕着端点从一个位置 旋转到另一个位置所成的图形叫做角.顶点ABO一、任意角的概念角——一点出发的两条射线所围成
的图形角——一条射线绕一个端点从一个位置旋转到另一个位置所形成的图形顶点始边终边一、任意角的概念规定:任意角正角:按逆时针方向旋转形成的角。如:360 °负角:按顺时针方向旋转形成的角.如:-120° 零角:射线不作旋转时形成的角. 0°终边与始边重合的角是零角吗?二、角的分类963前黄牌逆时针:450°即450°
顺时针:30°即-30°问题:如果教室的钟慢了5分钟,你应当如何将它校准?
如果教室的钟快了1.25小时,你应当如何将它校准?
当时间校准后,分针旋转了多少度?注意:(1)角的顶点于原点; 终边落在第几象限就是第几象限角. Ⅰ Ⅱ Ⅲ Ⅳ
其中Ⅰ,Ⅱ,Ⅲ,Ⅳ分别表示第一,二,三,四象限角三、象限角的定义(2)始边重合于x轴的非负半轴;课堂练习请指出下面的角是第几象限角?(1)-50°(2)405°(3)210°(4)-200°第四象限角第一象限角第三象限角第二象限角课堂练习请指出下面的角是第几象限角?(1)-50°(2)405°(3)210°(4)-200°1、锐角(钝角)是第几象限的角?2、第一象限的角是否都是锐角?3、小于90°的角都是锐角吗?第一(第二)象限的角不都是锐角小于90°的角并不都是锐角,
它还有可能是零角或负角。6.第二象限的角一定比第一象限的角大吗? 象限角只能反映角的终边所在象限,不能反映角的大小. 知识巩固4.终边相同的角大小相等吗?5. 大小相等的角终边相同吗?不一定一定相同不一定请指出下面的角是第几象限角?(1)-50°(2)405°(3)210°(4)-200°是第四象限的角是第一象限的角是第三象限的角是第二象限的角(5)-450°-450°轴线角如果角的终边落在了坐标轴上,就认为这个角不属于任何象限,称这样的角为轴线角.轴线角的定义你能举例说出其它的轴线角吗?思考1: -32°,328°,-392°是第几象限的角?
这些角有什么内在联系?-32°-392°o328°与-32°角终边相同的角有多少个?
这些角与-32°角在数量上相差多少? 五、终边相同的角思考2:所有与-32°角终边相同的角,连同-32°
角在内,可构成一个集合S,你能用描述法表
示集合S吗? S={β|β=-32°+k·360°,k∈Z}思考3:一般地,所有与角α终边相同的角,连同角
α在内所构成的集合S可以怎样表示? S={β|β=α+k·360°k∈Z}
即任一与α终边相同的角,都可以表示成角α与整数个周角的和.
???????????????????????????????????????????????????????????????????????????????????????????????????????????? 钱塘江一线潮伦敦之眼各种电波 现实世界中的很多运动,变化都有着循环往复、周而复始的现象。如何用数学的方法来刻画这种变化规律呢?
本章要学习的三角函数就是刻画这种变化规律的数学模型。必修四 第1章 三角函数
第1节 任意角学习过哪些不同范围的角?角的范围:0°至 360°体操中有转体两周半或转体三周,如何度量这些角度呢?新课2. 角的分类:1. 任意角的定义:3. 象限角与轴线角:4. 终边相同的角的表示法:一条射线绕端点从一个位置旋转到另一个位置所形成的图形.终边落在第几象限就是第几象限角.终边落在坐标轴上的角叫轴线角.正角、零角、负角.本课提纲:(阅读课本 P5-6完成下列问题)例题分析例1、在0°到360°范围内,找出与-950°12'角终边相同的角,并判定它是第几象限角;解:-950°12'=-1080°+129°48' =-3×360°+129°48'所以,-950°12'是第二象限的角因为129°48'是第二象限的角例2、写出终边在y轴上的角的集合.解:在0°~360°范围内,终边在y轴上的角有两
个,即90°,270°角(如图).
因此,所有与90°角终边相同的角构成集合
S1={β|β=90°+k·360°.k∈Z}.
而所有与270°角终边相同的角构成集合
S2={β|β=270°+k·360°.k∈Z}.例题分析于是,终边在y轴上的角的集合
S=S1∪S2
={β|β=90°+2k·180°,k∈Z }∪{β|β=90°+180°+2k·180°,k∈Z }
={β|β=90°+2k·180°,k∈Z } ∪{β|β=90°+(2k+1)180°,k∈Z }
={β|β=90°+n·180°,n∈Z }例题分析={β|β=90°+k·360°,k∈Z}∪{β|β=270°+k·360°,k∈Z} 思考1:终边在x轴正半轴、负半轴,y轴正半轴、负半轴、 x轴、y轴、坐标轴上的角分别如何表示? x轴正半轴:α= k·360°,k∈Z ;
x轴负半轴:α= 180°+k·360°,k∈Z ;
y轴正半轴:α= 90°+k·360°,k∈Z ;
y轴负半轴:α= 270°+k·360°,k∈Z ;
x轴:α= k·180°,k∈Z ;
y轴:α= 90°+k·180°,k∈Z ;
坐标轴:α= k·90°,k∈Z . 思考2:终边在直线y=x上的角分别如何表示? α= 45°+k·180°,k∈ZXYO第一象限的角表示为
第二象限的角表示为
第三象限的角表示为
第四象限的角表示为{?|k?360?旋转游戏1.初始时面朝的方向相同吗?2.终止时面朝的方向怎样?3.旋转的圈数不同有没有区别?从旋转的角度描述一下怎样可以得到一个角?一个确定的旋转应该包括哪些方面?从哪转的?转多少?怎样转的?角——有公共端点的两条射线所围成
的图形一、任意角的概念新的定义:平面内一条射线绕着端点从一个位置 旋转到另一个位置所成的图形叫做角.顶点ABO一、任意角的概念角——一点出发的两条射线所围成
的图形角——一条射线绕一个端点从一个位置旋转到另一个位置所形成的图形顶点始边终边一、任意角的概念规定:任意角正角:按逆时针方向旋转形成的角。如:360 °负角:按顺时针方向旋转形成的角.如:-120° 零角:射线不作旋转时形成的角. 0°终边与始边重合的角是零角吗?二、角的分类963前黄牌逆时针:450°即450°
顺时针:30°即-30°问题:如果教室的钟慢了5分钟,你应当如何将它校准?
如果教室的钟快了1.25小时,你应当如何将它校准?
当时间校准后,分针旋转了多少度?注意:(1)角的顶点于原点; 终边落在第几象限就是第几象限角. Ⅰ Ⅱ Ⅲ Ⅳ
其中Ⅰ,Ⅱ,Ⅲ,Ⅳ分别表示第一,二,三,四象限角三、象限角的定义(2)始边重合于x轴的非负半轴;课堂练习请指出下面的角是第几象限角?(1)-50°(2)405°(3)210°(4)-200°第四象限角第一象限角第三象限角第二象限角课堂练习请指出下面的角是第几象限角?(1)-50°(2)405°(3)210°(4)-200°1、锐角(钝角)是第几象限的角?2、第一象限的角是否都是锐角?3、小于90°的角都是锐角吗?第一(第二)象限的角不都是锐角小于90°的角并不都是锐角,
它还有可能是零角或负角。6.第二象限的角一定比第一象限的角大吗? 象限角只能反映角的终边所在象限,不能反映角的大小. 知识巩固4.终边相同的角大小相等吗?5. 大小相等的角终边相同吗?不一定一定相同不一定请指出下面的角是第几象限角?(1)-50°(2)405°(3)210°(4)-200°是第四象限的角是第一象限的角是第三象限的角是第二象限的角(5)-450°-450°轴线角如果角的终边落在了坐标轴上,就认为这个角不属于任何象限,称这样的角为轴线角.轴线角的定义你能举例说出其它的轴线角吗?思考1: -32°,328°,-392°是第几象限的角?
这些角有什么内在联系?-32°-392°o328°与-32°角终边相同的角有多少个?
这些角与-32°角在数量上相差多少? 五、终边相同的角思考2:所有与-32°角终边相同的角,连同-32°
角在内,可构成一个集合S,你能用描述法表
示集合S吗? S={β|β=-32°+k·360°,k∈Z}思考3:一般地,所有与角α终边相同的角,连同角
α在内所构成的集合S可以怎样表示? S={β|β=α+k·360°k∈Z}
即任一与α终边相同的角,都可以表示成角α与整数个周角的和.
