人教高中数学必修四1.4.1正弦函数余弦函数的图像(优质课)(共18张PPT)
文档属性
| 名称 | 人教高中数学必修四1.4.1正弦函数余弦函数的图像(优质课)(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-13 00:00:00 | ||
图片预览




文档简介
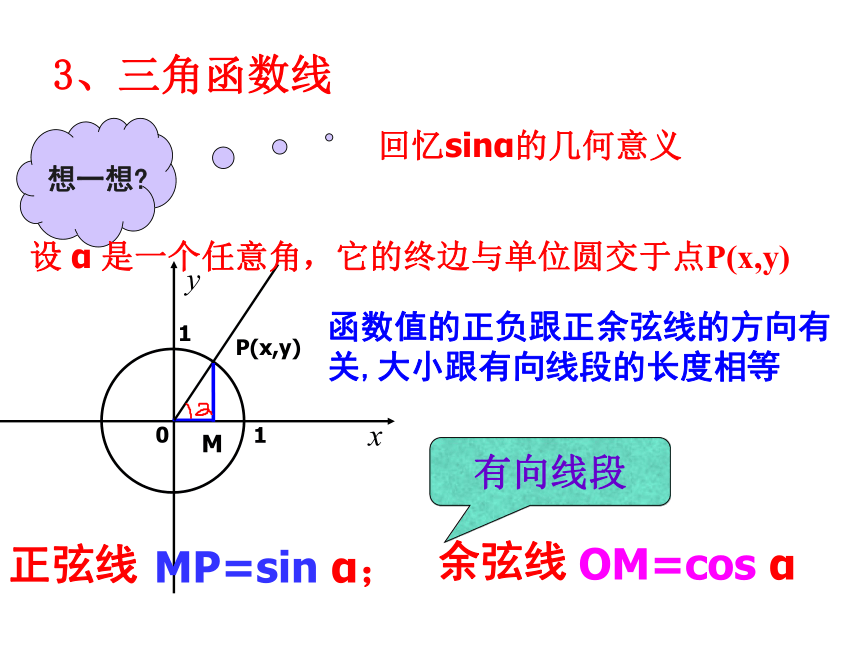
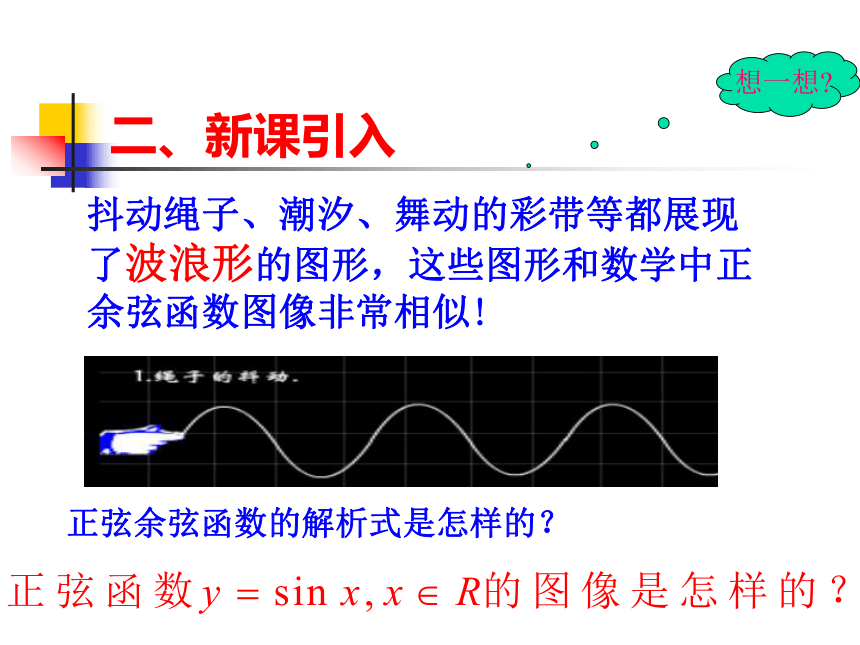
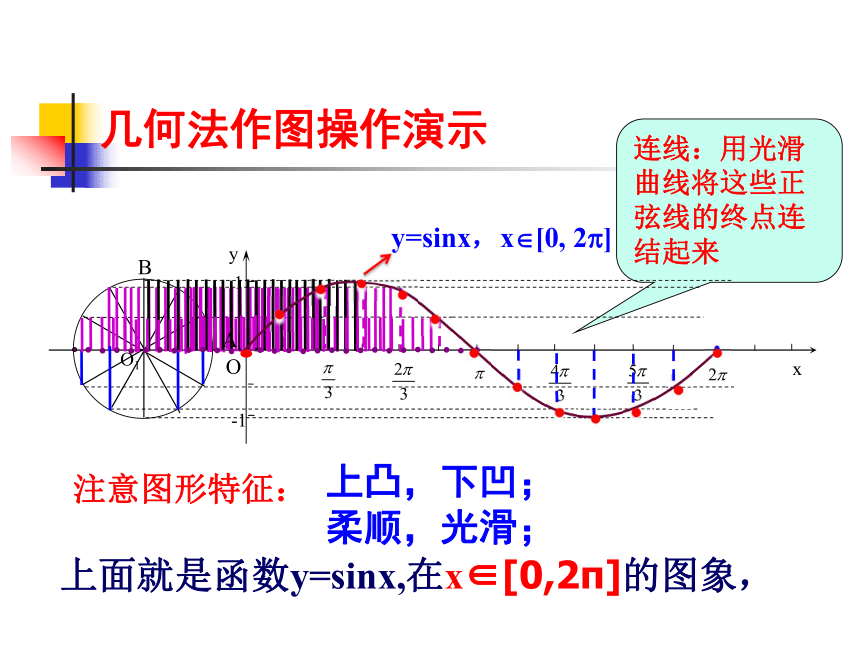
课件18张PPT。1.4.1正弦函数、余弦函数的图像(第一课时)1.正弦sinA=余弦cosA=一、复习活动,动动脑2、任意角的三角函数定义 那么其中想一想?有向线段正弦线余弦线3、三角函数线回忆sinα的几何意义设 α 是一个任意角,它的终边与单位圆交于点P(x,y)MP=sin α;OM=cos α函数值的正负跟正余弦线的方向有关,大小跟有向线段的长度相等二、新课引入抖动绳子、潮汐、舞动的彩带等都展现了波浪形的图形,这些图形和数学中正余弦函数图像非常相似!想一想?正弦余弦函数的解析式是怎样的?问题:如何画函数y=sinx,x∈[0,2π]的图象关键:是利用单位圆中角的正弦线,平移到直角坐标系中M我们把这种精确作图的方法称为几何法。步骤:三、沙海淘金列表、描点、连线连线:用光滑曲线将这些正弦线的终点连结起来AB上面就是函数y=sinx,在x∈[0,2π]的图象,几何法作图操作演示注意图形特征:上凸,下凹;
柔顺,光滑;
y=sinx,x?[0, 2?]五点:思考:我们作正弦函数y=sinx ,x∈[0,2 π]的图象时,描出了13个点,但其中起关键作用的点是哪些?分别说出它们的坐标。在精确度要求不太高时,如何快速地作出正弦函数的图象呢?
在作出正弦函数的图象时,应抓住哪些
关键点?思考 ?与x轴的交点图象的最高点图象的最低点五点作图法上面就是函数y=sinx,在x∈[0,2π]的图象五点作图法步骤:(1)列表(列出关键五点)(2)描点(描出五个关键点)(3)连线(用光滑曲线顺次连五个点) 思考 如何由y=sinx ,x?[0,2?] 的图象得到 y=sinx ,x?R的图象?y=sinx x?[0,2?]y=sinx x?R正弦曲线终边相同的角的三角函数值相等,所以y=sinx的图象在… [-4π,-2π] ,[-2π,0] ,[0,2π] ,[2π,4π]…上的图象与y=sinx,x∈[0,2π]的图象的形状完全一致.y=sinx x?[0,2?]y=sinx x?R利用图象平移余弦函数的图象 正弦函数的图象 余弦曲线正弦曲线形状完全一样只是位置不同探究 你能根据诱导公式,以正弦函数的图象为基础,通过适当的图形变换得到余弦函数的图象吗?余弦函数的图像余弦函数五点例1 画出下列函数的简图:
(1)y=sinx+1,x?[0, 2?]010-10 1 2 1 0 1 y=sinx,x?[0, 2?]y=sinx+1,x?[0, 2?]步骤:
1.列表
2.描点
3.连线向上平移1个单位四、小试牛刀解:由题意列表如下练习:作函数 y=2sinx-1,x∈[0,2π]的简图
五、挑战自我,合作愉快y=2sinx-1,x?[0, 2?]几何画板练习(1)作函数 ,x∈[0,2π]的简图(2)求方程 的实数根的个数。六、初露锋芒几何画板重点2.“五点作图法”1几何法作正弦函数的图象七、课后小结正弦五点:余弦五点:3、正余弦曲线:y=sinx,x?Ry=cosx,x?R再见 谢谢作业
1.总结本节课的知识,并进一步反思学习过程;
2.习题1.4 A组 1题;
3.利用所学知识探究五点法画余弦型函数图像
柔顺,光滑;
y=sinx,x?[0, 2?]五点:思考:我们作正弦函数y=sinx ,x∈[0,2 π]的图象时,描出了13个点,但其中起关键作用的点是哪些?分别说出它们的坐标。在精确度要求不太高时,如何快速地作出正弦函数的图象呢?
在作出正弦函数的图象时,应抓住哪些
关键点?思考 ?与x轴的交点图象的最高点图象的最低点五点作图法上面就是函数y=sinx,在x∈[0,2π]的图象五点作图法步骤:(1)列表(列出关键五点)(2)描点(描出五个关键点)(3)连线(用光滑曲线顺次连五个点) 思考 如何由y=sinx ,x?[0,2?] 的图象得到 y=sinx ,x?R的图象?y=sinx x?[0,2?]y=sinx x?R正弦曲线终边相同的角的三角函数值相等,所以y=sinx的图象在… [-4π,-2π] ,[-2π,0] ,[0,2π] ,[2π,4π]…上的图象与y=sinx,x∈[0,2π]的图象的形状完全一致.y=sinx x?[0,2?]y=sinx x?R利用图象平移余弦函数的图象 正弦函数的图象 余弦曲线正弦曲线形状完全一样只是位置不同探究 你能根据诱导公式,以正弦函数的图象为基础,通过适当的图形变换得到余弦函数的图象吗?余弦函数的图像余弦函数五点例1 画出下列函数的简图:
(1)y=sinx+1,x?[0, 2?]010-10 1 2 1 0 1 y=sinx,x?[0, 2?]y=sinx+1,x?[0, 2?]步骤:
1.列表
2.描点
3.连线向上平移1个单位四、小试牛刀解:由题意列表如下练习:作函数 y=2sinx-1,x∈[0,2π]的简图
五、挑战自我,合作愉快y=2sinx-1,x?[0, 2?]几何画板练习(1)作函数 ,x∈[0,2π]的简图(2)求方程 的实数根的个数。六、初露锋芒几何画板重点2.“五点作图法”1几何法作正弦函数的图象七、课后小结正弦五点:余弦五点:3、正余弦曲线:y=sinx,x?Ry=cosx,x?R再见 谢谢作业
1.总结本节课的知识,并进一步反思学习过程;
2.习题1.4 A组 1题;
3.利用所学知识探究五点法画余弦型函数图像
