2017-2018学年第二学期邯郸市育华中学九年级第2次月考数学试卷(含答案)
文档属性
| 名称 | 2017-2018学年第二学期邯郸市育华中学九年级第2次月考数学试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 191.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-13 13:18:08 | ||
图片预览



文档简介
初三第二次月考数学试卷
选择题(1-10小题,每题3分,11-16题,每题2分,共42分)
如图,AC为⊙O的直径,∠C=70°,则∠A为( )。
A. 40° B. 20° C. 30° D. 10°
在下列正方体的表面展开图中,剪掉1个正方形(阴影部分),剩余5个正方形组成中心对称图形的是( )。
三角形的外心是( )。
A. 三条边中线的交点 B. 三条边高的交点
C. 三条边垂直平分线的交点 D. 三条角平分线的交点
如图,AB是⊙O的直径,C、D是⊙O上位于AB异侧的两点,下列四个角中,一定与∠ACD相等的角是( )。
∠ADC B. ∠ABD C. ∠BAC D. ∠BAD
如图所示,△ABC与△关于点O成中心对称,则下列结论不成立的是( )。
A. 点A与点是关于点O的对称点 B. BO=
C. AB∥ D. ∠ACB=
如图,AB是⊙O的直径,==,∠COD=32°,则∠AEO的度数是( )。
A. 48° B. 56° C. 68° D. 78°
如图,在△AOB中,∠B=30°,将△AOB绕点O顺时针旋转52°得到△,边与边OB交于点C(不在OB上),则∠的度数为( )。
A. 22° B. 52° C. 60° D. 82°
如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为( )。
A. 130° B. 100° C. 65° D. 50°
在Rt△ABC中,∠C=90°,AC=2,BC=4,如果以点A为圆心,AC为半径作⊙A,那么斜边中点D与⊙A的位置关系是( )。
A. 点D在⊙A外 B. 点D在⊙A上 C. 点D在⊙A内 D. 无法确定
如图,∠AOB=110°,点C在⊙O上,且点C不与A、B重合,则∠ACB的度数为( )。
A. 55° B. 70°或125° C. 125° D. 55°或125°
如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=2,将菱形OABC绕原点顺时针旋转105°至的位置,则点的坐标为( )。
A. () B. ()
C. () D. ()
⊙O的半径为5cm,弦AB∥CD,且AB=6cm,CD=6cm,则AB与CB之间的距离为( )。
A. 1cm B. 7cm C. 3cm或4cm D. 1cm或7cm
如图,点A是量角器直径的一个动点,点B在半圆周上,点P在上,点Q在AB上,且PB=PQ,若点P对应140°(40°),则∠PQB的度数为( )。
A. 65° B. 70° C. 75° D. 80°
如图,在Rt△ABC中,∠C=90°,BC=3cm,AC=4cm,⊙O为Rt△ABC的内切圆,切点为D、E、F,则⊙O的半径为( )。
A. cm B. 1cm C. cm D. 2cm
在平面直角坐标系中,以点()为圆心,4为半径的圆( )。
A. 与x轴相交,与y轴相切 B. 与x轴相离,与y轴相交
C. 与x轴相切,与y轴相交 D. 与x轴相切,与y轴相离
如图,AB为⊙O的一固定直径,他把⊙O分成上、下两个半圆,过上半圆上一点C作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在上半圆(不包括A、B两点)上移动时,点P( )。
A. 到CD的距离保持不变 B. 位置不变
C.等分 D. 随点C的移动而移动
填空题(每空3分,共12分)
已知⊙O的半径为5,圆心O到弦AB的距离为3,则弦AB=________。
飞机着陆后滑行的距离s(单位:米)与滑行的时间t(单位:秒)之间的函数关系式是,飞机着陆后滑行______秒才能停下来。
如图,已知△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A,若∠MAB=30°,则∠B=______度。
如图,在平面直角坐标系中,四边形ABCO是正方形,点B的坐标为(),直线恰好把正方形ABCO的面积分成相等的两部分,则m=_______。
解答题:(21-24题每题10分,25题12分,26题14分)
(1)在平面直角坐标系中,抛物线经过A(﹣2,﹣4),O(0,0),B(2,0)三点,求抛物线的解析式。(5分)
(2)已知二次函数顶点为(),且函数图象与y轴交于(0,﹣4),求抛物线的解析式。(5分)
如图所示,每个小正方形的边长为1个单位长度,
(1)作出△ABC关于原点对称的△,并写出的坐标。(8分)
(2)y轴上有一点Q,使AQ+CQ的值最小,求点Q的坐标。(2分)
如图,⊙O经过点B,D,E,BD是⊙O的直径,∠C=90°,BE平分∠ABC。
(1)证明:直线AC是⊙O的切线。(5分)
(2)当AE=4,AD=2时,求⊙O的半径。(5分)
为衡量某特种车辆的性能,研究制定了行驶指数P,,而K的大小与平均速度v有关(不考虑其他因素),K由两部分的和组成,一部分与成正比,另一部分与 v成正比,在实验中得到了表中的数据。
速度v
2
8
指数P
13
10
写出P与v的函数关系式。(5分)
当v为何值时,P有最大值,P的最大值为多少?(5分)
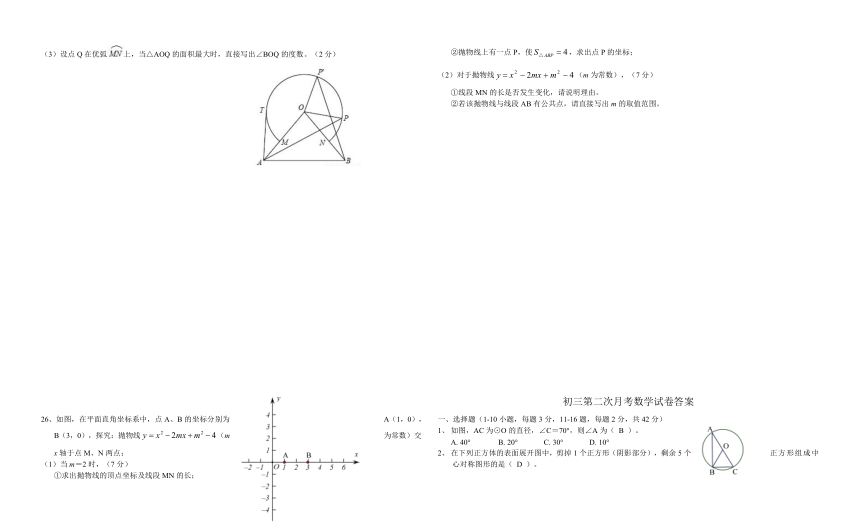
如图,△OAB中,OA=OB=10,∠AOB=80°,以点O为圆心,6为半径的优弧分别交OA、OB于点M,N。
(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得,求证:AP=BP;(5分)
(2)点T在左半弧上,若AT与弧相切,求点T到OA的距离;(5分)
(3)设点Q在优弧上,当△AOQ的面积最大时,直接写出∠BOQ的度数。(2分)
如图,在平面直角坐标系中,点A、B的坐标分别为A(1,0),B(3,0),探究:抛物线(m为常数)交x轴于点M、N两点;
(1)当m=2时,(7分)
①求出抛物线的顶点坐标及线段MN的长;
②抛物线上有一点P,使,求出点P的坐标;
(2)对于抛物线(m为常数),(7分)
①线段MN的长是否发生变化,请说明理由。
②若该抛物线与线段AB有公共点,请直接写出m的取值范围。
初三第二次月考数学试卷答案
选择题(1-10小题,每题3分,11-16题,每题2分,共42分)
如图,AC为⊙O的直径,∠C=70°,则∠A为( B )。
A. 40° B. 20° C. 30° D. 10°
在下列正方体的表面展开图中,剪掉1个正方形(阴影部分),剩余5个正方形组成中心对称图形的是( D )。
三角形的外心是( C )。
A. 三条边中线的交点 B. 三条边高的交点
C. 三条边垂直平分线的交点 D. 三条角平分线的交点
如图,AB是⊙O的直径,C、D是⊙O上位于AB异侧的两点,下列四个角中,一定与∠ACD相等的角是( B )。
∠ADC B. ∠ABD C. ∠BAC D. ∠BAD
如图所示,△ABC与△关于点O成中心对称,则下列结论不成立的是( D )。
A. 点A与点是关于点O的对称点 B. BO=
C. AB∥ D. ∠ACB=
如图,AB是⊙O的直径,==,∠COD=32°,则∠AEO的度数是( A )。
A. 48° B. 56° C. 68° D. 78°
如图,在△AOB中,∠B=30°,将△AOB绕点O顺时针旋转52°得到△,边与边OB交于点C(不在OB上),则∠的度数为( D )。
A. 22° B. 52° C. 60° D. 82°
如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为( C )。
A. 130° B. 100° C. 65° D. 50°
在Rt△ABC中,∠C=90°,AC=2,BC=4,如果以点A为圆心,AC为半径作⊙A,那么斜边中点D与⊙A的位置关系是( A )。
A. 点D在⊙A外 B. 点D在⊙A上 C. 点D在⊙A内 D. 无法确定
如图,∠AOB=110°,点C在⊙O上,且点C不与A、B重合,则∠ACB的度数为( D )。
A. 55° B. 70°或125° C. 125° D. 55°或125°
如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=2,将菱形OABC绕原点顺时针旋转105°至的位置,则点的坐标为( A )。
A. () B. ()
C. () D. ()
⊙O的半径为5cm,弦AB∥CD,且AB=6cm,CD=6cm,则AB与CB之间的距离为( D )。
A. 1cm B. 7cm C. 3cm或4cm D. 1cm或7cm
如图,点A是量角器直径的一个动点,点B在半圆周上,点P在上,点Q在AB上,且PB=PQ,若点P对应140°(40°),则∠PQB的度数为( B )。
A. 65° B. 70° C. 75° D. 80°
如图,在Rt△ABC中,∠C=90°,BC=3cm,AC=4cm,⊙O为Rt△ABC的内切圆,切点为D、E、F,则⊙O的半径为( B )。
A. cm B. 1cm C. cm D. 2cm
在平面直角坐标系中,以点()为圆心,4为半径的圆( C )。
A. 与x轴相交,与y轴相切 B. 与x轴相离,与y轴相交
C. 与x轴相切,与y轴相交 D. 与x轴相切,与y轴相离
如图,AB为⊙O的一固定直径,他把⊙O分成上、下两个半圆,过上半圆上一点C作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在上半圆(不包括A、B两点)上移动时,点P( B )。
A. 到CD的距离保持不变 B. 位置不变
C.等分 D. 随点C的移动而移动
填空题(每空3分,共12分)
已知⊙O的半径为5,圆心O到弦AB的距离为3,则弦AB=____8____。
飞机着陆后滑行的距离s(单位:米)与滑行的时间t(单位:秒)之间的函数关系式是,飞机着陆后滑行____20____秒才能停下来。
如图,已知△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A,若∠MAB=30°,则∠B=____60____度。
如图,在平面直角坐标系中,四边形ABCO是正方形,点B的坐标为(),直线恰好把正方形ABCO的面积分成相等的两部分,则m=____2____。
解答题:(21-24题每题10分,25题12分,26题14分)
(1)在平面直角坐标系中,抛物线经过A(﹣2,﹣4),O(0,0),B(2,0)三点,求抛物线的解析式。(5分)
(2)已知二次函数顶点为(),且函数图象与y轴交于(0,﹣4),求抛物线的解析式。(5分)
解:(1)将A(﹣2,﹣4),O(0,0),B(2,0)三点代入得,
,解得:
∴;
(2)设二次函数解析式为,
将(0,﹣4)代入解析式得:
a=,
∴
如图所示,每个小正方形的边长为1个单位长度,
(1)作出△ABC关于原点对称的△,并写出的坐标。(8分)
(2)y轴上有一点Q,使AQ+CQ的值最小,求点Q的坐标。(2分)
解:(1)如图,A1(2,﹣2),B1(3,0),C1(1,1);
(2)Q(0,0)。
如图,⊙O经过点B,D,E,BD是⊙O的直径,∠C=90°,BE平分∠ABC。
(1)证明:直线AC是⊙O的切线。(5分)
(2)当AE=4,AD=2时,求⊙O的半径。(5分)
(1)证明:连接OE,
∵BE是∠ABC的平分线,
∴∠1=∠2,
∵OE=OB,
∴∠1=∠3,
∴∠2=∠3,
∵OE∥BC,
又∠C=90°,
∴∠AEO=90°,
∴AC是⊙O的切线;
(2)解:设⊙O的半径为r,在Rt△AEO中,由勾股定理可得
OA2=OE2+AE2,
∵AE=4,AD=2,
∴,
∴r=3。
为衡量某特种车辆的性能,研究制定了行驶指数P,,而K的大小与平均速度v有关(不考虑其他因素),K由两部分的和组成,一部分与成正比,另一部分与 v成正比,在实验中得到了表中的数据。
速度v
2
8
指数P
13
10
(1)写出P与v的函数关系式。(5分)
(2)当v为何值时,P有最大值,P的最大值为多少?(5分)
解:(1)设,
由表中数据得:,
解得:,
∴;
(2)对称轴,
将v=4代入解析式得P=14,
∴当v为4时,P有最大值,P的最大值为14。
如图,△OAB中,OA=OB=10,∠AOB=80°,以点O为圆心,6为半径的优弧分别交OA、OB于点M,N。
(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得,求证:AP=BP;(5分)
(2)点T在左半弧上,若AT与弧相切,求点T到OA的距离;(5分)
(3)设点Q在优弧上,当△AOQ的面积最大时,直接写出∠BOQ的度数。(2分)
(1)证明:如图1,∵∠AOP=∠AOB+∠BOP=80°+∠BOP,
∠BOP′=∠POP′+∠BOP=80°+∠BOP,
∴∠AOP=∠BOP′。
∵在△AOP和△BOP′中,,
∴△AOP≌△BOP′(SAS)。
∴AP=BP′。
(2)连接OT,过点T作TH⊥OA于点H,
∵AT与⊙O相切,∴∠ATO=90°。
∴。
∵×OA×TH=×AT×OT,
∴×10×TH=×8×6,解得:TH=。
∴点T到OA的距离为
如图2,当OQ⊥OA时,△AOQ的面积最大。理由如下:
当Q点在优弧左侧上,
∵OQ⊥OA,
∴QO是△AOQ中最长的高,则△AOQ的面积最大。
∴∠BOQ=∠AOQ+∠AOB=90°+80°=170°。
当Q点在优弧MN右侧上,
∵OQ⊥OA,
∴QO是△AOQ中最长的高,则△AOQ的面积最大。
∴∠BOQ=∠AOQ-∠AOB=90°-80°=10°。
综上所述:当∠BOQ的度数为10°或170°时,△AOQ的面积最大。
如图,在平面直角坐标系中,点A、B的坐标分别为A(1,0),B(3,0),探究:抛物线(m为常数)交x轴于点M、N两点;
(1)当m=2时,(7分)
①求出抛物线的顶点坐标及线段MN的长;
②抛物线上有一点P,使,求出点P的坐标;
(2)对于抛物线(m为常数),(7分)
①线段MN的长是否发生变化,请说明理由。
②若该抛物线与线段AB有公共点,请直接写出m的取值范围。
解:(1)当m=2时,抛物线解析式为 ,
①顶点坐标:(2,﹣4),MN=4;
②∵AB=2,,
∴△ABP底边AB上的高为4,
令y=4得,令y=﹣4得x=2,
∴P的坐标为(,4),(,4),(2,﹣4)。
(2)①不变,理由如下:
令y=0得,
∴MN=m+2-(m-2)=4,
②﹣1≤m≤1或3≤m≤5。
选择题(1-10小题,每题3分,11-16题,每题2分,共42分)
如图,AC为⊙O的直径,∠C=70°,则∠A为( )。
A. 40° B. 20° C. 30° D. 10°
在下列正方体的表面展开图中,剪掉1个正方形(阴影部分),剩余5个正方形组成中心对称图形的是( )。
三角形的外心是( )。
A. 三条边中线的交点 B. 三条边高的交点
C. 三条边垂直平分线的交点 D. 三条角平分线的交点
如图,AB是⊙O的直径,C、D是⊙O上位于AB异侧的两点,下列四个角中,一定与∠ACD相等的角是( )。
∠ADC B. ∠ABD C. ∠BAC D. ∠BAD
如图所示,△ABC与△关于点O成中心对称,则下列结论不成立的是( )。
A. 点A与点是关于点O的对称点 B. BO=
C. AB∥ D. ∠ACB=
如图,AB是⊙O的直径,==,∠COD=32°,则∠AEO的度数是( )。
A. 48° B. 56° C. 68° D. 78°
如图,在△AOB中,∠B=30°,将△AOB绕点O顺时针旋转52°得到△,边与边OB交于点C(不在OB上),则∠的度数为( )。
A. 22° B. 52° C. 60° D. 82°
如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为( )。
A. 130° B. 100° C. 65° D. 50°
在Rt△ABC中,∠C=90°,AC=2,BC=4,如果以点A为圆心,AC为半径作⊙A,那么斜边中点D与⊙A的位置关系是( )。
A. 点D在⊙A外 B. 点D在⊙A上 C. 点D在⊙A内 D. 无法确定
如图,∠AOB=110°,点C在⊙O上,且点C不与A、B重合,则∠ACB的度数为( )。
A. 55° B. 70°或125° C. 125° D. 55°或125°
如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=2,将菱形OABC绕原点顺时针旋转105°至的位置,则点的坐标为( )。
A. () B. ()
C. () D. ()
⊙O的半径为5cm,弦AB∥CD,且AB=6cm,CD=6cm,则AB与CB之间的距离为( )。
A. 1cm B. 7cm C. 3cm或4cm D. 1cm或7cm
如图,点A是量角器直径的一个动点,点B在半圆周上,点P在上,点Q在AB上,且PB=PQ,若点P对应140°(40°),则∠PQB的度数为( )。
A. 65° B. 70° C. 75° D. 80°
如图,在Rt△ABC中,∠C=90°,BC=3cm,AC=4cm,⊙O为Rt△ABC的内切圆,切点为D、E、F,则⊙O的半径为( )。
A. cm B. 1cm C. cm D. 2cm
在平面直角坐标系中,以点()为圆心,4为半径的圆( )。
A. 与x轴相交,与y轴相切 B. 与x轴相离,与y轴相交
C. 与x轴相切,与y轴相交 D. 与x轴相切,与y轴相离
如图,AB为⊙O的一固定直径,他把⊙O分成上、下两个半圆,过上半圆上一点C作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在上半圆(不包括A、B两点)上移动时,点P( )。
A. 到CD的距离保持不变 B. 位置不变
C.等分 D. 随点C的移动而移动
填空题(每空3分,共12分)
已知⊙O的半径为5,圆心O到弦AB的距离为3,则弦AB=________。
飞机着陆后滑行的距离s(单位:米)与滑行的时间t(单位:秒)之间的函数关系式是,飞机着陆后滑行______秒才能停下来。
如图,已知△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A,若∠MAB=30°,则∠B=______度。
如图,在平面直角坐标系中,四边形ABCO是正方形,点B的坐标为(),直线恰好把正方形ABCO的面积分成相等的两部分,则m=_______。
解答题:(21-24题每题10分,25题12分,26题14分)
(1)在平面直角坐标系中,抛物线经过A(﹣2,﹣4),O(0,0),B(2,0)三点,求抛物线的解析式。(5分)
(2)已知二次函数顶点为(),且函数图象与y轴交于(0,﹣4),求抛物线的解析式。(5分)
如图所示,每个小正方形的边长为1个单位长度,
(1)作出△ABC关于原点对称的△,并写出的坐标。(8分)
(2)y轴上有一点Q,使AQ+CQ的值最小,求点Q的坐标。(2分)
如图,⊙O经过点B,D,E,BD是⊙O的直径,∠C=90°,BE平分∠ABC。
(1)证明:直线AC是⊙O的切线。(5分)
(2)当AE=4,AD=2时,求⊙O的半径。(5分)
为衡量某特种车辆的性能,研究制定了行驶指数P,,而K的大小与平均速度v有关(不考虑其他因素),K由两部分的和组成,一部分与成正比,另一部分与 v成正比,在实验中得到了表中的数据。
速度v
2
8
指数P
13
10
写出P与v的函数关系式。(5分)
当v为何值时,P有最大值,P的最大值为多少?(5分)
如图,△OAB中,OA=OB=10,∠AOB=80°,以点O为圆心,6为半径的优弧分别交OA、OB于点M,N。
(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得,求证:AP=BP;(5分)
(2)点T在左半弧上,若AT与弧相切,求点T到OA的距离;(5分)
(3)设点Q在优弧上,当△AOQ的面积最大时,直接写出∠BOQ的度数。(2分)
如图,在平面直角坐标系中,点A、B的坐标分别为A(1,0),B(3,0),探究:抛物线(m为常数)交x轴于点M、N两点;
(1)当m=2时,(7分)
①求出抛物线的顶点坐标及线段MN的长;
②抛物线上有一点P,使,求出点P的坐标;
(2)对于抛物线(m为常数),(7分)
①线段MN的长是否发生变化,请说明理由。
②若该抛物线与线段AB有公共点,请直接写出m的取值范围。
初三第二次月考数学试卷答案
选择题(1-10小题,每题3分,11-16题,每题2分,共42分)
如图,AC为⊙O的直径,∠C=70°,则∠A为( B )。
A. 40° B. 20° C. 30° D. 10°
在下列正方体的表面展开图中,剪掉1个正方形(阴影部分),剩余5个正方形组成中心对称图形的是( D )。
三角形的外心是( C )。
A. 三条边中线的交点 B. 三条边高的交点
C. 三条边垂直平分线的交点 D. 三条角平分线的交点
如图,AB是⊙O的直径,C、D是⊙O上位于AB异侧的两点,下列四个角中,一定与∠ACD相等的角是( B )。
∠ADC B. ∠ABD C. ∠BAC D. ∠BAD
如图所示,△ABC与△关于点O成中心对称,则下列结论不成立的是( D )。
A. 点A与点是关于点O的对称点 B. BO=
C. AB∥ D. ∠ACB=
如图,AB是⊙O的直径,==,∠COD=32°,则∠AEO的度数是( A )。
A. 48° B. 56° C. 68° D. 78°
如图,在△AOB中,∠B=30°,将△AOB绕点O顺时针旋转52°得到△,边与边OB交于点C(不在OB上),则∠的度数为( D )。
A. 22° B. 52° C. 60° D. 82°
如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为( C )。
A. 130° B. 100° C. 65° D. 50°
在Rt△ABC中,∠C=90°,AC=2,BC=4,如果以点A为圆心,AC为半径作⊙A,那么斜边中点D与⊙A的位置关系是( A )。
A. 点D在⊙A外 B. 点D在⊙A上 C. 点D在⊙A内 D. 无法确定
如图,∠AOB=110°,点C在⊙O上,且点C不与A、B重合,则∠ACB的度数为( D )。
A. 55° B. 70°或125° C. 125° D. 55°或125°
如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=2,将菱形OABC绕原点顺时针旋转105°至的位置,则点的坐标为( A )。
A. () B. ()
C. () D. ()
⊙O的半径为5cm,弦AB∥CD,且AB=6cm,CD=6cm,则AB与CB之间的距离为( D )。
A. 1cm B. 7cm C. 3cm或4cm D. 1cm或7cm
如图,点A是量角器直径的一个动点,点B在半圆周上,点P在上,点Q在AB上,且PB=PQ,若点P对应140°(40°),则∠PQB的度数为( B )。
A. 65° B. 70° C. 75° D. 80°
如图,在Rt△ABC中,∠C=90°,BC=3cm,AC=4cm,⊙O为Rt△ABC的内切圆,切点为D、E、F,则⊙O的半径为( B )。
A. cm B. 1cm C. cm D. 2cm
在平面直角坐标系中,以点()为圆心,4为半径的圆( C )。
A. 与x轴相交,与y轴相切 B. 与x轴相离,与y轴相交
C. 与x轴相切,与y轴相交 D. 与x轴相切,与y轴相离
如图,AB为⊙O的一固定直径,他把⊙O分成上、下两个半圆,过上半圆上一点C作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在上半圆(不包括A、B两点)上移动时,点P( B )。
A. 到CD的距离保持不变 B. 位置不变
C.等分 D. 随点C的移动而移动
填空题(每空3分,共12分)
已知⊙O的半径为5,圆心O到弦AB的距离为3,则弦AB=____8____。
飞机着陆后滑行的距离s(单位:米)与滑行的时间t(单位:秒)之间的函数关系式是,飞机着陆后滑行____20____秒才能停下来。
如图,已知△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A,若∠MAB=30°,则∠B=____60____度。
如图,在平面直角坐标系中,四边形ABCO是正方形,点B的坐标为(),直线恰好把正方形ABCO的面积分成相等的两部分,则m=____2____。
解答题:(21-24题每题10分,25题12分,26题14分)
(1)在平面直角坐标系中,抛物线经过A(﹣2,﹣4),O(0,0),B(2,0)三点,求抛物线的解析式。(5分)
(2)已知二次函数顶点为(),且函数图象与y轴交于(0,﹣4),求抛物线的解析式。(5分)
解:(1)将A(﹣2,﹣4),O(0,0),B(2,0)三点代入得,
,解得:
∴;
(2)设二次函数解析式为,
将(0,﹣4)代入解析式得:
a=,
∴
如图所示,每个小正方形的边长为1个单位长度,
(1)作出△ABC关于原点对称的△,并写出的坐标。(8分)
(2)y轴上有一点Q,使AQ+CQ的值最小,求点Q的坐标。(2分)
解:(1)如图,A1(2,﹣2),B1(3,0),C1(1,1);
(2)Q(0,0)。
如图,⊙O经过点B,D,E,BD是⊙O的直径,∠C=90°,BE平分∠ABC。
(1)证明:直线AC是⊙O的切线。(5分)
(2)当AE=4,AD=2时,求⊙O的半径。(5分)
(1)证明:连接OE,
∵BE是∠ABC的平分线,
∴∠1=∠2,
∵OE=OB,
∴∠1=∠3,
∴∠2=∠3,
∵OE∥BC,
又∠C=90°,
∴∠AEO=90°,
∴AC是⊙O的切线;
(2)解:设⊙O的半径为r,在Rt△AEO中,由勾股定理可得
OA2=OE2+AE2,
∵AE=4,AD=2,
∴,
∴r=3。
为衡量某特种车辆的性能,研究制定了行驶指数P,,而K的大小与平均速度v有关(不考虑其他因素),K由两部分的和组成,一部分与成正比,另一部分与 v成正比,在实验中得到了表中的数据。
速度v
2
8
指数P
13
10
(1)写出P与v的函数关系式。(5分)
(2)当v为何值时,P有最大值,P的最大值为多少?(5分)
解:(1)设,
由表中数据得:,
解得:,
∴;
(2)对称轴,
将v=4代入解析式得P=14,
∴当v为4时,P有最大值,P的最大值为14。
如图,△OAB中,OA=OB=10,∠AOB=80°,以点O为圆心,6为半径的优弧分别交OA、OB于点M,N。
(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得,求证:AP=BP;(5分)
(2)点T在左半弧上,若AT与弧相切,求点T到OA的距离;(5分)
(3)设点Q在优弧上,当△AOQ的面积最大时,直接写出∠BOQ的度数。(2分)
(1)证明:如图1,∵∠AOP=∠AOB+∠BOP=80°+∠BOP,
∠BOP′=∠POP′+∠BOP=80°+∠BOP,
∴∠AOP=∠BOP′。
∵在△AOP和△BOP′中,,
∴△AOP≌△BOP′(SAS)。
∴AP=BP′。
(2)连接OT,过点T作TH⊥OA于点H,
∵AT与⊙O相切,∴∠ATO=90°。
∴。
∵×OA×TH=×AT×OT,
∴×10×TH=×8×6,解得:TH=。
∴点T到OA的距离为
如图2,当OQ⊥OA时,△AOQ的面积最大。理由如下:
当Q点在优弧左侧上,
∵OQ⊥OA,
∴QO是△AOQ中最长的高,则△AOQ的面积最大。
∴∠BOQ=∠AOQ+∠AOB=90°+80°=170°。
当Q点在优弧MN右侧上,
∵OQ⊥OA,
∴QO是△AOQ中最长的高,则△AOQ的面积最大。
∴∠BOQ=∠AOQ-∠AOB=90°-80°=10°。
综上所述:当∠BOQ的度数为10°或170°时,△AOQ的面积最大。
如图,在平面直角坐标系中,点A、B的坐标分别为A(1,0),B(3,0),探究:抛物线(m为常数)交x轴于点M、N两点;
(1)当m=2时,(7分)
①求出抛物线的顶点坐标及线段MN的长;
②抛物线上有一点P,使,求出点P的坐标;
(2)对于抛物线(m为常数),(7分)
①线段MN的长是否发生变化,请说明理由。
②若该抛物线与线段AB有公共点,请直接写出m的取值范围。
解:(1)当m=2时,抛物线解析式为 ,
①顶点坐标:(2,﹣4),MN=4;
②∵AB=2,,
∴△ABP底边AB上的高为4,
令y=4得,令y=﹣4得x=2,
∴P的坐标为(,4),(,4),(2,﹣4)。
(2)①不变,理由如下:
令y=0得,
∴MN=m+2-(m-2)=4,
②﹣1≤m≤1或3≤m≤5。
同课章节目录
