2018沪科版数学九年级下第24章《圆》单元测试卷(含答案)
文档属性
| 名称 | 2018沪科版数学九年级下第24章《圆》单元测试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 362.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-14 00:00:00 | ||
图片预览



文档简介
第24章圆单元测试卷
一、选择题
如图,半径为2cm,圆心角为的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为
A. B. C. D.
下列说法中正确的是
A. 平分弦的直径垂直于弦 B. 圆心角是圆周角的2倍 C. 三角形的外心到三角形各边的距离相等 D. 从圆外一点可以引圆的两条切线,这一点和圆心的连线平分两条切线的夹角
用一个圆心角为,半径为3的扇形作一个圆锥的侧面,则这个圆锥的底面半径为
A. B. 1 C. D. 2
下面说法正确的是
A. 一个三角形经过适当的旋转得到的图形和原图形可组成平行四边形 B. 一个三角形经过适当的平移,前后图形可组成平行四边形 C. 因为正方形也可以看作菱形,故菱形经过适当的旋转可得到正方形 D. 夹在两平行直线之间的线段相等
在中,是AB的中点,以C为圆心,4cm长为半径作圆,则四点中,在圆内的有
A. 4个 B. 3个 C. 2个 D. 1个
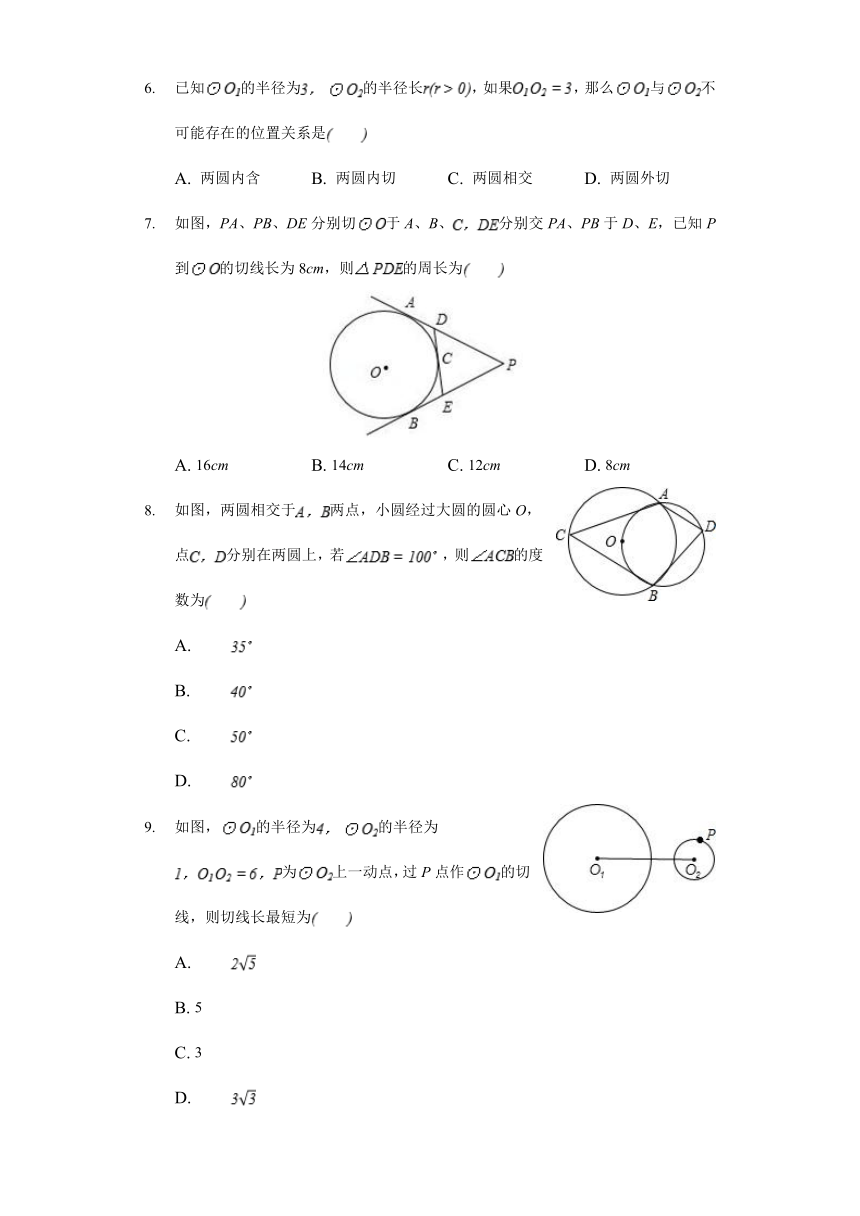
已知的半径为的半径长,如果,那么与不可能存在的位置关系是
A. 两圆内含 B. 两圆内切 C. 两圆相交 D. 两圆外切
如图,PA、PB、DE分别切于A、B、分别交PA、PB于D、E,已知P到的切线长为8cm,则的周长为
A. 16cm B. 14cm C. 12cm D. 8cm
如图,两圆相交于两点,小圆经过大圆的圆心O,点分别在两圆上,若,则的度数为
A. B. C. D.
如图,的半径为的半径为为上一动点,过P点作的切线,则切线长最短为
A. B. 5 C. 3 D.
二、填空题
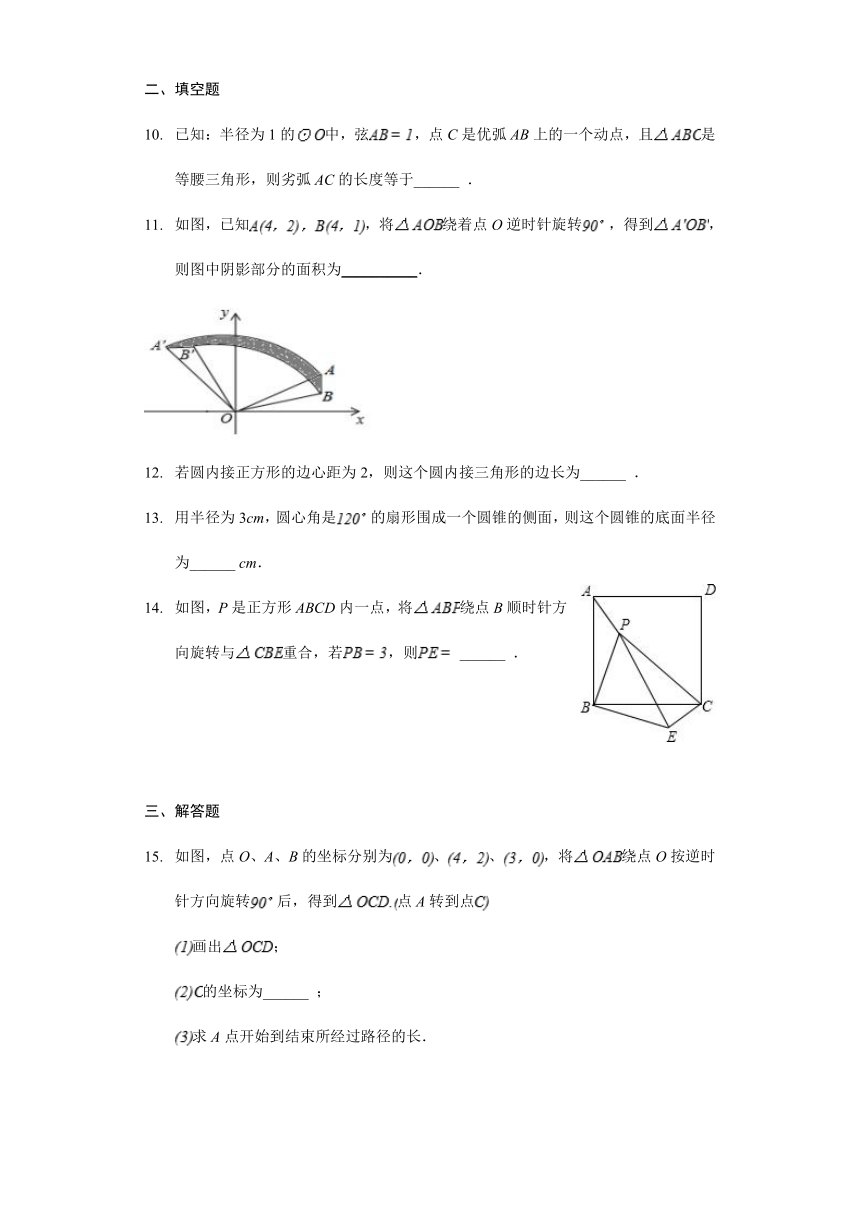
已知:半径为1的中,弦,点C是优弧AB上的一个动点,且是等腰三角形,则劣弧AC的长度等于______ .
如图,已知,将绕着点O逆时针旋转,得到,则图中阴影部分的面积为__________.
若圆内接正方形的边心距为2,则这个圆内接三角形的边长为______ .
用半径为3cm,圆心角是的扇形围成一个圆锥的侧面,则这个圆锥的底面半径为______ cm.
如图,P是正方形ABCD内一点,将绕点B顺时针方向旋转与重合,若,则 ______ .
三、解答题
如图,点O、A、B的坐标分别为、、,将绕点O按逆时针方向旋转后,得到点A转到点 画出; 的坐标为______ ; 求A点开始到结束所经过路径的长.
如图,的直径AB的长为10,弦AC的长为的平分线交于点D. 求BC的长;求弦BD的长.
???如图,已知是的外接圆,AB是的直径,D是AB延长线的一点,交DC的延长线于 ?于F,且. 求证:DE是的切线; 若,求AE和BC的长.
如图,四边形ABCD为矩形,E为BC边中点,以AD为直径的与AE交于点F. 求证:四边形AOCE为平行四边形; 求证:CF与相切; 若F为AE的中点,求的大小.
如图,在中,,以AB为直径的交AC于点,垂足为E. 求证:DE是的切线; 若,垂足为点F,交于点半径为5,求劣弧DG的长结果保留
【答案】
1. A 2. D 3. B 4. A 5. C 6. D 7. A 8. B 9. C
10. ??
11. ??
12. ??
13. 1??
14. ??
15. ??
16. 解: 为直径, , ; 如图,连接BD,同理可知, 平分, , , , ,解得.??
17. 证明:连接OC;
,又, , , , , , 是的切线; , ??, 在中,, , 在中,, ????, 在中,, ? ? ??
??
18. 证明:四边形ABCD是矩形, , 为BC边中点,, , , 四边形OAEC是平行四边形; 如图1,连接OF, 四边形OAEC是平行四边形 , , , , , , 在与中,, ≌, , , 与相切; 如图2,连接DE, 是直径, , 点F为AE的中点, 为AE的垂直平分线, , 在与中, , ≌, , , 三角形ADE为等边三角形, , .??
19. 证明:如图1,连接BD、OD, 是直径, , , , , , 是的中位线, , , , 为半径, 是切线; 解:如图2所示,连接 过圆心O, 弧弧BD, , , , , 劣弧DG的长是??
一、选择题
如图,半径为2cm,圆心角为的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为
A. B. C. D.
下列说法中正确的是
A. 平分弦的直径垂直于弦 B. 圆心角是圆周角的2倍 C. 三角形的外心到三角形各边的距离相等 D. 从圆外一点可以引圆的两条切线,这一点和圆心的连线平分两条切线的夹角
用一个圆心角为,半径为3的扇形作一个圆锥的侧面,则这个圆锥的底面半径为
A. B. 1 C. D. 2
下面说法正确的是
A. 一个三角形经过适当的旋转得到的图形和原图形可组成平行四边形 B. 一个三角形经过适当的平移,前后图形可组成平行四边形 C. 因为正方形也可以看作菱形,故菱形经过适当的旋转可得到正方形 D. 夹在两平行直线之间的线段相等
在中,是AB的中点,以C为圆心,4cm长为半径作圆,则四点中,在圆内的有
A. 4个 B. 3个 C. 2个 D. 1个
已知的半径为的半径长,如果,那么与不可能存在的位置关系是
A. 两圆内含 B. 两圆内切 C. 两圆相交 D. 两圆外切
如图,PA、PB、DE分别切于A、B、分别交PA、PB于D、E,已知P到的切线长为8cm,则的周长为
A. 16cm B. 14cm C. 12cm D. 8cm
如图,两圆相交于两点,小圆经过大圆的圆心O,点分别在两圆上,若,则的度数为
A. B. C. D.
如图,的半径为的半径为为上一动点,过P点作的切线,则切线长最短为
A. B. 5 C. 3 D.
二、填空题
已知:半径为1的中,弦,点C是优弧AB上的一个动点,且是等腰三角形,则劣弧AC的长度等于______ .
如图,已知,将绕着点O逆时针旋转,得到,则图中阴影部分的面积为__________.
若圆内接正方形的边心距为2,则这个圆内接三角形的边长为______ .
用半径为3cm,圆心角是的扇形围成一个圆锥的侧面,则这个圆锥的底面半径为______ cm.
如图,P是正方形ABCD内一点,将绕点B顺时针方向旋转与重合,若,则 ______ .
三、解答题
如图,点O、A、B的坐标分别为、、,将绕点O按逆时针方向旋转后,得到点A转到点 画出; 的坐标为______ ; 求A点开始到结束所经过路径的长.
如图,的直径AB的长为10,弦AC的长为的平分线交于点D. 求BC的长;求弦BD的长.
???如图,已知是的外接圆,AB是的直径,D是AB延长线的一点,交DC的延长线于 ?于F,且. 求证:DE是的切线; 若,求AE和BC的长.
如图,四边形ABCD为矩形,E为BC边中点,以AD为直径的与AE交于点F. 求证:四边形AOCE为平行四边形; 求证:CF与相切; 若F为AE的中点,求的大小.
如图,在中,,以AB为直径的交AC于点,垂足为E. 求证:DE是的切线; 若,垂足为点F,交于点半径为5,求劣弧DG的长结果保留
【答案】
1. A 2. D 3. B 4. A 5. C 6. D 7. A 8. B 9. C
10. ??
11. ??
12. ??
13. 1??
14. ??
15. ??
16. 解: 为直径, , ; 如图,连接BD,同理可知, 平分, , , , ,解得.??
17. 证明:连接OC;
,又, , , , , , 是的切线; , ??, 在中,, , 在中,, ????, 在中,, ? ? ??
??
18. 证明:四边形ABCD是矩形, , 为BC边中点,, , , 四边形OAEC是平行四边形; 如图1,连接OF, 四边形OAEC是平行四边形 , , , , , , 在与中,, ≌, , , 与相切; 如图2,连接DE, 是直径, , 点F为AE的中点, 为AE的垂直平分线, , 在与中, , ≌, , , 三角形ADE为等边三角形, , .??
19. 证明:如图1,连接BD、OD, 是直径, , , , , , 是的中位线, , , , 为半径, 是切线; 解:如图2所示,连接 过圆心O, 弧弧BD, , , , , 劣弧DG的长是??
