2017-2018学年黑龙江省大庆市杜尔伯特县八年级上期末数学试卷(五四学制)原卷+解析
文档属性
| 名称 | 2017-2018学年黑龙江省大庆市杜尔伯特县八年级上期末数学试卷(五四学制)原卷+解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 242.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-14 00:00:00 | ||
图片预览



文档简介
2017-2018学年黑龙江省大庆市杜尔伯特县八年级(上)期末数学试卷(五四学制)
一、选择题(每题3分,共30分在每小题给出的四个选项中只有一个选项符合要求)
1.(3分)下列图案中,不是中心对称图形的是( )
A. B. C. D.
2.(3分)下列各式:(1﹣x),,,,其中分式共有( )
A.1个 B.2个 C.3个 D.4个
3.(3分)已知x>y,则下列不等式不成立的是( )
A.x﹣6>y﹣6 B.3x>3y C.﹣2x<﹣2y D.﹣3x+6>﹣3y+6
4.(3分)到三角形三个顶点的距离相等的点是三角形( )的交点.
A.三个内角平分线 B.三边垂直平分线
C.三条中线 D.三条高
5.(3分)如果 ABCD的周长为40cm,△ABC的周长为25cm,则对角线AC的长是( )
A.5cm B.15cm C.6cm D.16cm
6.(3分)下列不能判定一个四边形是平行四边形的是( )
A.两组对边分别平行的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行另一组对边相等的四边形是平行四边形
D.对角线互相平分的四边形是平行四边形
7.(3分)已知等腰三角形的两边长分别为5和6,则这个等腰三角形的周长为( )
A.11 B.16 C.17 D.16或17
8.(3分)多项式2x2﹣2y2分解因式的结果是( )
A.2(x+y)2 B.2(x﹣y)2 C.2(x+y)(x﹣y) D.2(y+x)(y﹣x)
9.(3分)已知△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,则△ABC的腰和底边长分别为( )
A.24cm和12cm B.16cm和22cm C.20cm和16cm D.22cm和16cm
10.(3分)A,B两地相距48千米,一艘轮船从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时,已知水流速度为4千米/时,若设该轮船在静水中的速度为x千米/时,则可列方程( )
A. B.
C. +4=9 D.
二、填空题(每小题3分,共30分)
11.(3分)请写出解集为x<3的不等式: .(写出一个即可)
12.(3分)如图,△ABC中,D、E分别是AB、AC的中点,若BC=4cm,则DE= cm.
13.(3分)如图所示,在 ABCD中,对角线AC、BD相交于点O,已知△BOC与△AOB的周长之差为4, ABCD的周长为28,则BC的长度为 .
14.(3分)已知点P(m﹣3,m+1)在第一象限,则m的取值范围是 .
15.(3分)根据变化完成式子的变形: =.
16.(3分)一个多边形的内角和与外角和的比是4:1,则它的边数是 .
17.(3分)当x= 时,分式的值等于零.
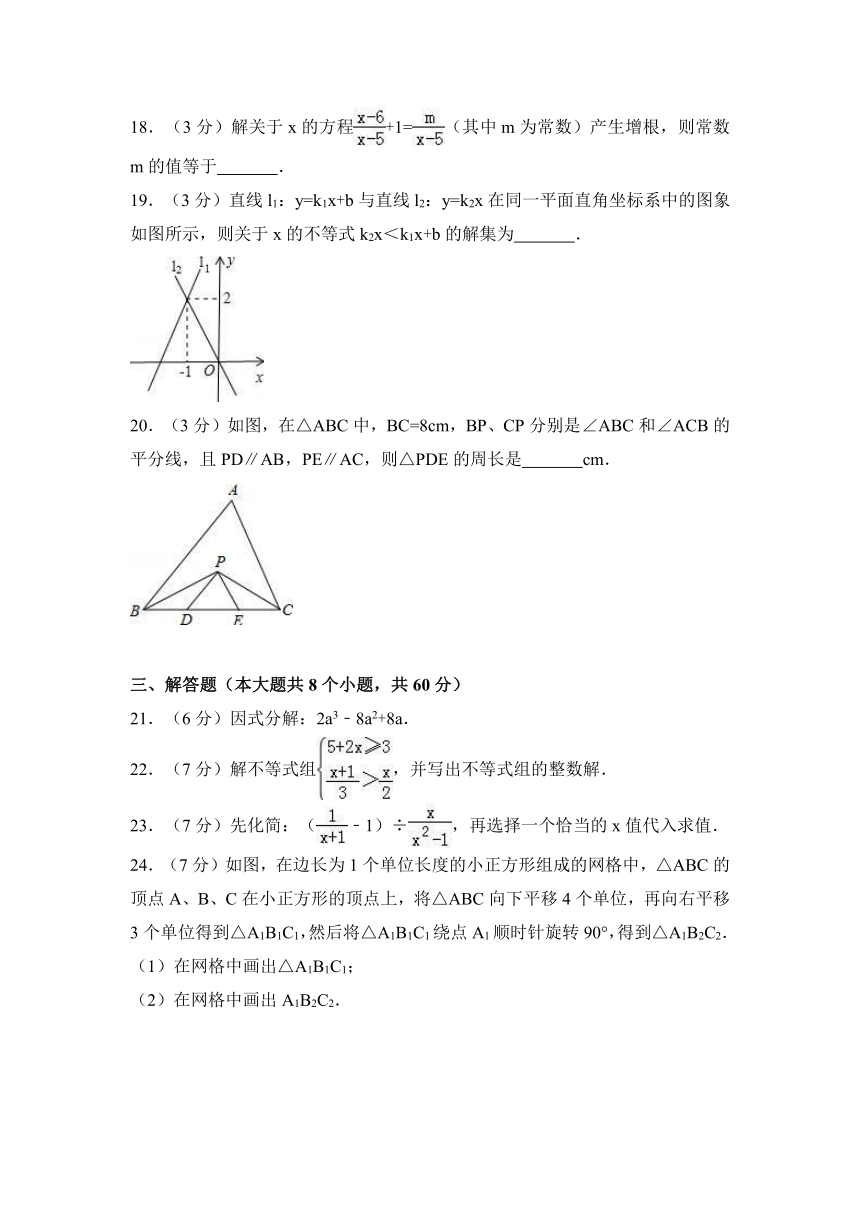
18.(3分)解关于x的方程+1=(其中m为常数)产生增根,则常数m的值等于 .
19.(3分)直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x<k1x+b的解集为 .
20.(3分)如图,在△ABC中,BC=8cm,BP、CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC,则△PDE的周长是 cm.
三、解答题(本大题共8个小题,共60分)
21.(6分)因式分解:2a3﹣8a2+8a.
22.(7分)解不等式组,并写出不等式组的整数解.
23.(7分)先化简:(﹣1)÷,再选择一个恰当的x值代入求值.
24.(7分)如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位,再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°,得到△A1B2C2.
(1)在网格中画出△A1B1C1;
(2)在网格中画出A1B2C2.
25.(7分)解分式方程:﹣1=.
26.(8分)为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两间工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品?
27.(9分)某饮料厂以300千克的A种果汁和240千克的B种果汁为原料,配制生产甲、乙两种新型饮料,已知每千克甲种饮料含0.6千克A种果汁,含0.3千克B种果汁;每千克乙种饮料含0.2千克A种果汁,含0.4千克B种果汁.饮料厂计划生产甲、乙两种新型饮料共650千克,设该厂生产甲种饮料x(千克).
(1)列出满足题意的关于x的不等式组,并求出x的取值范围;
(2)已知该饮料厂的甲种饮料销售价是每1千克3元,乙种饮料销售价是每1千克4元,那么该饮料厂生产甲、乙两种饮料各多少千克,才能使得这批饮料销售总金额最大?
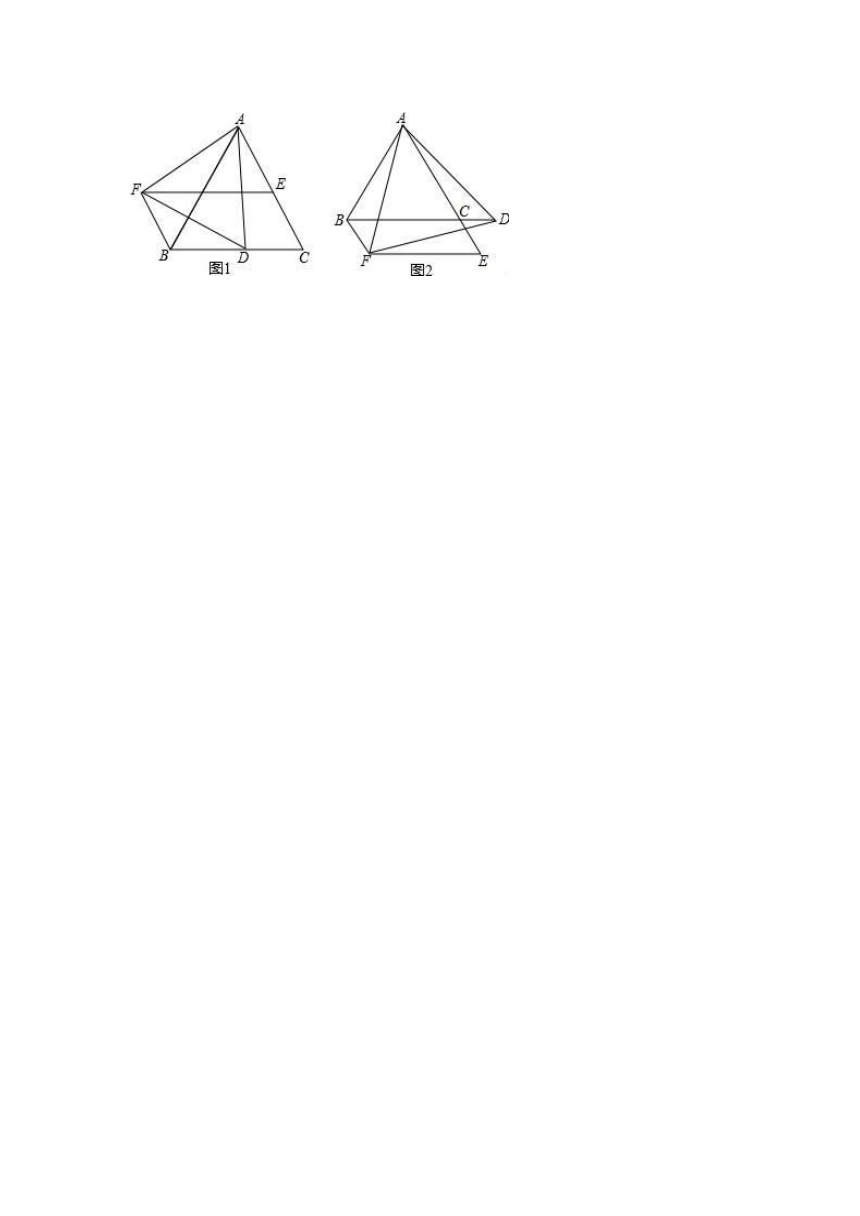
28.(9分)已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC 边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
2017-2018学年黑龙江省大庆市杜尔伯特县八年级(上)期末数学试卷(五四学制)
参考答案与试题解析
一、选择题(每题3分,共30分在每小题给出的四个选项中只有一个选项符合要求)
1.(3分)下列图案中,不是中心对称图形的是( )
A. B. C. D.
【解答】解:只有选项C连接相应各点后是正三角形,绕中心旋转180度后所得的图形与原图形不会重合.
故选:C.
2.(3分)下列各式:(1﹣x),,,,其中分式共有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:(1﹣x)是整式,不是分式;
,的分母中均不含有字母,因此它们是整式,而不是分式.
分母中含有字母,因此是分式.
故选:A.
3.(3分)已知x>y,则下列不等式不成立的是( )
A.x﹣6>y﹣6 B.3x>3y C.﹣2x<﹣2y D.﹣3x+6>﹣3y+6
【解答】解:A、∵x>y,∴x﹣6>y﹣6,故本选项错误;
B、∵x>y,∴3x>3y,故本选项错误;
C、∵x>y,∴﹣x<﹣y,∴﹣2x<﹣2y,故选项错误;
D、∵x>y,∴﹣3x<﹣3y,∴﹣3x+6<﹣3y+6,故本选项正确.
故选:D.
4.(3分)到三角形三个顶点的距离相等的点是三角形( )的交点.
A.三个内角平分线 B.三边垂直平分线
C.三条中线 D.三条高
【解答】解:到三角形三个顶点的距离相等的点是三角形三边垂直平分线的交点.
故选:B.
5.(3分)如果 ABCD的周长为40cm,△ABC的周长为25cm,则对角线AC的长是( )
A. 5cm B.15cm C.6cm D.16cm
【解答】解:如图所示:∵ ABCD的周长为40cm,△ABC的周长为25cm,
∴AB+BC=20cm,
∴AC=25﹣20=5(cm).
故选:A.
6.(3分)下列不能判定一个四边形是平行四边形的是( )
A.两组对边分别平行的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行另一组对边相等的四边形是平行四边形
D.对角线互相平分的四边形是平行四边形
【解答】解:根据平行四边形的判定定理,A、B、D均符合是平行四边形的条件,C则不能判定是平行四边形.
故选:C.
7.(3分)已知等腰三角形的两边长分别为5和6,则这个等腰三角形的周长为( )
A.11 B.16 C.17 D.16或17
【解答】解:①6是腰长时,三角形的三边分别为6、6、5,
能组成三角形,
周长=6+6+5=17;
②6是底边时,三角形的三边分别为6、5、5,
能组成三角形,
周长=6+5+5=16.
综上所述,三角形的周长为16或17.
故选:D.
8.(3分)多项式2x2﹣2y2分解因式的结果是( )
A.2(x+y)2 B.2(x﹣y)2 C.2(x+y)(x﹣y) D.2(y+x)(y﹣x)
【解答】解:2x2﹣2y2=2(x2﹣y2)=2(x+y)(x﹣y),
故选:C.
9.(3分)已知△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,则△ABC的腰和底边长分别为( )
A.24cm和12cm B.16cm和22cm C.20cm和16cm D.22cm和16cm
【解答】解:如图,连接BD,
∵D在线段AB的垂直平分线上,
∴BD=AD,
∴BD+DC+BC=AC+BC=38cm,
且AB+AC+BC=60cm,
∴AB=60cm﹣38cm=22cm,
∴AC=22cm,
∴BC=38cm﹣AC=38cm﹣22cm=16cm,
即等腰三角形的腰为22cm,底为16cm,
故选:D.
10.(3分)A,B两地相距48千米,一艘轮船从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时,已知水流速度为4千米/时,若设该轮船在静水中的速度为x千米/时,则可列方程( )
A. B.
C. +4=9 D.
【解答】解:顺流时间为:;逆流时间为:.
所列方程为: +=9.
故选: A.
二、填空题(每小题3分,共30分)
11.(3分)请写出解集为x<3的不等式: x﹣3<0(答案不唯一) .(写出一个即可)
【解答】解:移项,得
x﹣3<0(答案不唯一).
故答案为x﹣3<0(答案不唯一).
12.(3分)如图,△ABC中,D、E分别是AB、AC的中点,若BC=4cm,则DE= 2 cm.
【解答】解:∵点D、E分别为△ABC的边AB、AC的中点,
∴DE是△ABC的中位线,
∴DE=BC.
又∵BC=4cm,
∴DE=2cm.
故答案为:2.
13.(3分)如图所示,在 ABCD中,对角线AC、BD相交于点O,已知△BOC与△AOB的周长之差为4, ABCD的周长为28,则BC的长度为 9 .
【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC,OB=OD,
∵ ABCD的周长为28,
∴BC+AB=14①,
∵△BOC与△AOB的周长之差为4,
∴(OB+OC+BC)﹣(OA+OB+AB)=4,
即BC﹣AB=4 ②,
由①+②得:2BC=18,
∴BC=9;
故答案为:9
14.(3分)已知点P(m﹣3,m+1)在第一象限,则m的取值范围是 m>3 .
【解答】解:∵点P(m﹣3,m+1)在第一象限,
∴,
解得m>3.
15.(3分)根据变化完成式子的变形: =.
【解答】解:提取公因式,得,
=,
分式有意义,则y≠0且x﹣y≠0,
化简得,原式=;
故答案为:y
16.(3分)一个多边形的内角和与外角和的比是4:1,则它的边数是 10 .
【解答】解:根据题意,得
(n﹣2) 180=1440,
解得:n=10.
则此多边形的边数是10.
故答案为:10.
17.(3分)当x= ﹣2 时,分式的值等于零.
【解答】解:∵分式的值等于零,
∴,
∴,
∴x=﹣2.
故答案为:﹣2
18.(3分)解关于x的方程+1=(其中m为常数)产生增根,则常数m的值等于 ﹣1 .
【解答】解:去分母得:x﹣6+x﹣5=m,
由分式方程有增根,得到x﹣5=0,即x=5,
把x=5代入整式方程得:m=﹣1,
故答案为:﹣1.
19.(3分)直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x<k1x+b的解集为 x>﹣1 .
【解答】解:关于x的不等式k2x<k1x+b的解集为x>﹣1.
故答案是:x>﹣1.
20.(3分)如图,在△ABC中,BC=8cm,BP、CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC,则△PDE的周长是 8 cm.
【解答】解:∵BP、CP分别是∠ABC和∠ACB的角平分线,
∴∠ABP=∠PBD,∠ACP=∠PCE,
∵PD∥AB,PE∥AC,
∴∠ABP=∠BPD,∠ACP=∠CPE,
∴∠PBD=∠BPD,∠PCE=∠CPE,
∴BD=PD,CE=PE,
∴△PDE的周长=PD+DE+PE=BD+DE+EC=BC=8cm.
故答案是:8.
三、解答题(本大题共8个小题,共60分)
21.(6分)因式分解:2a3﹣8a2+8a.
【解答】解:2a3﹣8a2+8a
=2a(a2﹣4a+4)
=2a(a﹣2)2
22.(7分)解不等式组,并写出不等式组的整数解.
【解答】解:解不等我是5+2x≥3,得:x≥﹣1,
解不等式>,得:x<2,
则不等式组的解集是﹣1≤x<2,
所以不等式组的整数解是﹣1,0,1.
23.(7分)先化简:(﹣1)÷,再选择一个恰当的x值代入求值.
【解答】解:原式=(﹣)
=
=﹣x+1
当x=2时,原式=﹣2+1=﹣1
24.(7分)如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位,再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°,得到△A1B2C2.
(1)在网格中画出△A1B1C1;
(2)在网格中画出A1B2C2.
【解答】解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求.
25.(7分)解分式方程:﹣1=.
【解答】解:方程两边同时乘以(x+2)(x﹣2)得:
(x﹣2)2﹣(x+2)(x﹣2)=16
解得:x=﹣2,
检验:当x=﹣2时,(x+2)(x﹣2)=0,
∴x=﹣2是原方程的增根,原方程无解.
26.(8分)为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两间工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品?
【解答】解:设甲工厂每天加工x件产品,则乙工厂每天加工1.5x件产品,
依题意得﹣=10,
解得:x=40.
经检验:x=40是原方程的根,且符合题意.所以1.5x=60.
答:甲工厂每天加工40件产品,乙工厂每天加工60件产品.
27.(9分)某饮料厂以300千克的A种果汁和240千克的B种果汁为原料,配制生产甲、乙两种新型饮料,已知每千克甲种饮料含0.6千克A种果汁,含0.3千克B种果汁;每千克乙种饮料含0.2千克A种果汁,含0.4千克B种果汁.饮料厂计划生产甲、乙两种新型饮料共650千克,设该厂生产甲种饮料x(千克).
(1)列出满足题意的关于x的不等式组,并求出x的取值范围;
(2)已知该饮料厂的甲种饮料销售价是每1千克3元,乙种饮料销售价是每1千克4元,那么该饮料厂生产甲、乙两种饮料各多少千克,才能使得这批饮料销售总金额最大?
【解答】解:(1)设该厂生产甲种饮料x千克,则生产乙种饮料(650﹣x)千克,
根据题意得,,
由①得,x≤425,
由②得,x≥200,
所以,x的取值范围是200≤x≤425;
(2)设这批饮料销售总金额为y元,
根据题意得,y=3x+4(650﹣x)=3x+2600﹣4x=﹣x+2600,
即y=﹣x+2600,
∵k=﹣1<0,
∴y随x的增大而减小,
∴当x=200时,这批饮料销售总金额最大,
则650﹣x=650﹣200=450.
故该饮料厂生产甲种饮料200千克,乙种饮料450千克,才能使得这批饮料销售总金额最大.
28.(9分)已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC 边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
【解答】证明:(1)∵△ABC和△ADF都是等边三角形,
∴AF=AD,AB=AC,∠FAD=∠BAC=60°,
又∵∠FAB=∠FAD﹣∠BAD,∠DAC=∠BAC﹣∠BAD,
∴∠FAB=∠DAC,
在△AFB和△ADC中,
,
∴△AFB≌△ADC(SAS);
(2)由①得△AFB≌△ADC,
∴∠ABF=∠C=60°.
又∵∠BAC=∠C=60°,
∴∠ABF=∠BAC,
∴FB∥AC,
又∵BC∥EF,
∴四边形BCEF是平行四边形;
(3)成立,理由如下:
∵△ABC和△ADF都是等边三角形,
∴AF=AD,AB=AC,∠FAD=∠BAC=60°,
又∵∠FAB=∠BAC﹣∠FAE,∠DAC=∠FAD﹣∠FAE,
∴∠FAB=∠DAC,
在△AFB和△ADC中,
,
∴△AFB≌△ADC(SAS);
∴∠AFB=∠ADC.
又∵∠ADC+∠DAC=60°,∠EAF+∠DAC=60°,
∴∠ADC=∠EAF,
∴∠AFB=∠EAF,
∴BF∥AE,
又∵BC∥EF,
∴四边形BCEF是平行四边形.
一、选择题(每题3分,共30分在每小题给出的四个选项中只有一个选项符合要求)
1.(3分)下列图案中,不是中心对称图形的是( )
A. B. C. D.
2.(3分)下列各式:(1﹣x),,,,其中分式共有( )
A.1个 B.2个 C.3个 D.4个
3.(3分)已知x>y,则下列不等式不成立的是( )
A.x﹣6>y﹣6 B.3x>3y C.﹣2x<﹣2y D.﹣3x+6>﹣3y+6
4.(3分)到三角形三个顶点的距离相等的点是三角形( )的交点.
A.三个内角平分线 B.三边垂直平分线
C.三条中线 D.三条高
5.(3分)如果 ABCD的周长为40cm,△ABC的周长为25cm,则对角线AC的长是( )
A.5cm B.15cm C.6cm D.16cm
6.(3分)下列不能判定一个四边形是平行四边形的是( )
A.两组对边分别平行的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行另一组对边相等的四边形是平行四边形
D.对角线互相平分的四边形是平行四边形
7.(3分)已知等腰三角形的两边长分别为5和6,则这个等腰三角形的周长为( )
A.11 B.16 C.17 D.16或17
8.(3分)多项式2x2﹣2y2分解因式的结果是( )
A.2(x+y)2 B.2(x﹣y)2 C.2(x+y)(x﹣y) D.2(y+x)(y﹣x)
9.(3分)已知△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,则△ABC的腰和底边长分别为( )
A.24cm和12cm B.16cm和22cm C.20cm和16cm D.22cm和16cm
10.(3分)A,B两地相距48千米,一艘轮船从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时,已知水流速度为4千米/时,若设该轮船在静水中的速度为x千米/时,则可列方程( )
A. B.
C. +4=9 D.
二、填空题(每小题3分,共30分)
11.(3分)请写出解集为x<3的不等式: .(写出一个即可)
12.(3分)如图,△ABC中,D、E分别是AB、AC的中点,若BC=4cm,则DE= cm.
13.(3分)如图所示,在 ABCD中,对角线AC、BD相交于点O,已知△BOC与△AOB的周长之差为4, ABCD的周长为28,则BC的长度为 .
14.(3分)已知点P(m﹣3,m+1)在第一象限,则m的取值范围是 .
15.(3分)根据变化完成式子的变形: =.
16.(3分)一个多边形的内角和与外角和的比是4:1,则它的边数是 .
17.(3分)当x= 时,分式的值等于零.
18.(3分)解关于x的方程+1=(其中m为常数)产生增根,则常数m的值等于 .
19.(3分)直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x<k1x+b的解集为 .
20.(3分)如图,在△ABC中,BC=8cm,BP、CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC,则△PDE的周长是 cm.
三、解答题(本大题共8个小题,共60分)
21.(6分)因式分解:2a3﹣8a2+8a.
22.(7分)解不等式组,并写出不等式组的整数解.
23.(7分)先化简:(﹣1)÷,再选择一个恰当的x值代入求值.
24.(7分)如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位,再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°,得到△A1B2C2.
(1)在网格中画出△A1B1C1;
(2)在网格中画出A1B2C2.
25.(7分)解分式方程:﹣1=.
26.(8分)为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两间工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品?
27.(9分)某饮料厂以300千克的A种果汁和240千克的B种果汁为原料,配制生产甲、乙两种新型饮料,已知每千克甲种饮料含0.6千克A种果汁,含0.3千克B种果汁;每千克乙种饮料含0.2千克A种果汁,含0.4千克B种果汁.饮料厂计划生产甲、乙两种新型饮料共650千克,设该厂生产甲种饮料x(千克).
(1)列出满足题意的关于x的不等式组,并求出x的取值范围;
(2)已知该饮料厂的甲种饮料销售价是每1千克3元,乙种饮料销售价是每1千克4元,那么该饮料厂生产甲、乙两种饮料各多少千克,才能使得这批饮料销售总金额最大?
28.(9分)已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC 边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
2017-2018学年黑龙江省大庆市杜尔伯特县八年级(上)期末数学试卷(五四学制)
参考答案与试题解析
一、选择题(每题3分,共30分在每小题给出的四个选项中只有一个选项符合要求)
1.(3分)下列图案中,不是中心对称图形的是( )
A. B. C. D.
【解答】解:只有选项C连接相应各点后是正三角形,绕中心旋转180度后所得的图形与原图形不会重合.
故选:C.
2.(3分)下列各式:(1﹣x),,,,其中分式共有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:(1﹣x)是整式,不是分式;
,的分母中均不含有字母,因此它们是整式,而不是分式.
分母中含有字母,因此是分式.
故选:A.
3.(3分)已知x>y,则下列不等式不成立的是( )
A.x﹣6>y﹣6 B.3x>3y C.﹣2x<﹣2y D.﹣3x+6>﹣3y+6
【解答】解:A、∵x>y,∴x﹣6>y﹣6,故本选项错误;
B、∵x>y,∴3x>3y,故本选项错误;
C、∵x>y,∴﹣x<﹣y,∴﹣2x<﹣2y,故选项错误;
D、∵x>y,∴﹣3x<﹣3y,∴﹣3x+6<﹣3y+6,故本选项正确.
故选:D.
4.(3分)到三角形三个顶点的距离相等的点是三角形( )的交点.
A.三个内角平分线 B.三边垂直平分线
C.三条中线 D.三条高
【解答】解:到三角形三个顶点的距离相等的点是三角形三边垂直平分线的交点.
故选:B.
5.(3分)如果 ABCD的周长为40cm,△ABC的周长为25cm,则对角线AC的长是( )
A. 5cm B.15cm C.6cm D.16cm
【解答】解:如图所示:∵ ABCD的周长为40cm,△ABC的周长为25cm,
∴AB+BC=20cm,
∴AC=25﹣20=5(cm).
故选:A.
6.(3分)下列不能判定一个四边形是平行四边形的是( )
A.两组对边分别平行的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行另一组对边相等的四边形是平行四边形
D.对角线互相平分的四边形是平行四边形
【解答】解:根据平行四边形的判定定理,A、B、D均符合是平行四边形的条件,C则不能判定是平行四边形.
故选:C.
7.(3分)已知等腰三角形的两边长分别为5和6,则这个等腰三角形的周长为( )
A.11 B.16 C.17 D.16或17
【解答】解:①6是腰长时,三角形的三边分别为6、6、5,
能组成三角形,
周长=6+6+5=17;
②6是底边时,三角形的三边分别为6、5、5,
能组成三角形,
周长=6+5+5=16.
综上所述,三角形的周长为16或17.
故选:D.
8.(3分)多项式2x2﹣2y2分解因式的结果是( )
A.2(x+y)2 B.2(x﹣y)2 C.2(x+y)(x﹣y) D.2(y+x)(y﹣x)
【解答】解:2x2﹣2y2=2(x2﹣y2)=2(x+y)(x﹣y),
故选:C.
9.(3分)已知△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,则△ABC的腰和底边长分别为( )
A.24cm和12cm B.16cm和22cm C.20cm和16cm D.22cm和16cm
【解答】解:如图,连接BD,
∵D在线段AB的垂直平分线上,
∴BD=AD,
∴BD+DC+BC=AC+BC=38cm,
且AB+AC+BC=60cm,
∴AB=60cm﹣38cm=22cm,
∴AC=22cm,
∴BC=38cm﹣AC=38cm﹣22cm=16cm,
即等腰三角形的腰为22cm,底为16cm,
故选:D.
10.(3分)A,B两地相距48千米,一艘轮船从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时,已知水流速度为4千米/时,若设该轮船在静水中的速度为x千米/时,则可列方程( )
A. B.
C. +4=9 D.
【解答】解:顺流时间为:;逆流时间为:.
所列方程为: +=9.
故选: A.
二、填空题(每小题3分,共30分)
11.(3分)请写出解集为x<3的不等式: x﹣3<0(答案不唯一) .(写出一个即可)
【解答】解:移项,得
x﹣3<0(答案不唯一).
故答案为x﹣3<0(答案不唯一).
12.(3分)如图,△ABC中,D、E分别是AB、AC的中点,若BC=4cm,则DE= 2 cm.
【解答】解:∵点D、E分别为△ABC的边AB、AC的中点,
∴DE是△ABC的中位线,
∴DE=BC.
又∵BC=4cm,
∴DE=2cm.
故答案为:2.
13.(3分)如图所示,在 ABCD中,对角线AC、BD相交于点O,已知△BOC与△AOB的周长之差为4, ABCD的周长为28,则BC的长度为 9 .
【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC,OB=OD,
∵ ABCD的周长为28,
∴BC+AB=14①,
∵△BOC与△AOB的周长之差为4,
∴(OB+OC+BC)﹣(OA+OB+AB)=4,
即BC﹣AB=4 ②,
由①+②得:2BC=18,
∴BC=9;
故答案为:9
14.(3分)已知点P(m﹣3,m+1)在第一象限,则m的取值范围是 m>3 .
【解答】解:∵点P(m﹣3,m+1)在第一象限,
∴,
解得m>3.
15.(3分)根据变化完成式子的变形: =.
【解答】解:提取公因式,得,
=,
分式有意义,则y≠0且x﹣y≠0,
化简得,原式=;
故答案为:y
16.(3分)一个多边形的内角和与外角和的比是4:1,则它的边数是 10 .
【解答】解:根据题意,得
(n﹣2) 180=1440,
解得:n=10.
则此多边形的边数是10.
故答案为:10.
17.(3分)当x= ﹣2 时,分式的值等于零.
【解答】解:∵分式的值等于零,
∴,
∴,
∴x=﹣2.
故答案为:﹣2
18.(3分)解关于x的方程+1=(其中m为常数)产生增根,则常数m的值等于 ﹣1 .
【解答】解:去分母得:x﹣6+x﹣5=m,
由分式方程有增根,得到x﹣5=0,即x=5,
把x=5代入整式方程得:m=﹣1,
故答案为:﹣1.
19.(3分)直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x<k1x+b的解集为 x>﹣1 .
【解答】解:关于x的不等式k2x<k1x+b的解集为x>﹣1.
故答案是:x>﹣1.
20.(3分)如图,在△ABC中,BC=8cm,BP、CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC,则△PDE的周长是 8 cm.
【解答】解:∵BP、CP分别是∠ABC和∠ACB的角平分线,
∴∠ABP=∠PBD,∠ACP=∠PCE,
∵PD∥AB,PE∥AC,
∴∠ABP=∠BPD,∠ACP=∠CPE,
∴∠PBD=∠BPD,∠PCE=∠CPE,
∴BD=PD,CE=PE,
∴△PDE的周长=PD+DE+PE=BD+DE+EC=BC=8cm.
故答案是:8.
三、解答题(本大题共8个小题,共60分)
21.(6分)因式分解:2a3﹣8a2+8a.
【解答】解:2a3﹣8a2+8a
=2a(a2﹣4a+4)
=2a(a﹣2)2
22.(7分)解不等式组,并写出不等式组的整数解.
【解答】解:解不等我是5+2x≥3,得:x≥﹣1,
解不等式>,得:x<2,
则不等式组的解集是﹣1≤x<2,
所以不等式组的整数解是﹣1,0,1.
23.(7分)先化简:(﹣1)÷,再选择一个恰当的x值代入求值.
【解答】解:原式=(﹣)
=
=﹣x+1
当x=2时,原式=﹣2+1=﹣1
24.(7分)如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位,再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°,得到△A1B2C2.
(1)在网格中画出△A1B1C1;
(2)在网格中画出A1B2C2.
【解答】解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求.
25.(7分)解分式方程:﹣1=.
【解答】解:方程两边同时乘以(x+2)(x﹣2)得:
(x﹣2)2﹣(x+2)(x﹣2)=16
解得:x=﹣2,
检验:当x=﹣2时,(x+2)(x﹣2)=0,
∴x=﹣2是原方程的增根,原方程无解.
26.(8分)为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两间工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品?
【解答】解:设甲工厂每天加工x件产品,则乙工厂每天加工1.5x件产品,
依题意得﹣=10,
解得:x=40.
经检验:x=40是原方程的根,且符合题意.所以1.5x=60.
答:甲工厂每天加工40件产品,乙工厂每天加工60件产品.
27.(9分)某饮料厂以300千克的A种果汁和240千克的B种果汁为原料,配制生产甲、乙两种新型饮料,已知每千克甲种饮料含0.6千克A种果汁,含0.3千克B种果汁;每千克乙种饮料含0.2千克A种果汁,含0.4千克B种果汁.饮料厂计划生产甲、乙两种新型饮料共650千克,设该厂生产甲种饮料x(千克).
(1)列出满足题意的关于x的不等式组,并求出x的取值范围;
(2)已知该饮料厂的甲种饮料销售价是每1千克3元,乙种饮料销售价是每1千克4元,那么该饮料厂生产甲、乙两种饮料各多少千克,才能使得这批饮料销售总金额最大?
【解答】解:(1)设该厂生产甲种饮料x千克,则生产乙种饮料(650﹣x)千克,
根据题意得,,
由①得,x≤425,
由②得,x≥200,
所以,x的取值范围是200≤x≤425;
(2)设这批饮料销售总金额为y元,
根据题意得,y=3x+4(650﹣x)=3x+2600﹣4x=﹣x+2600,
即y=﹣x+2600,
∵k=﹣1<0,
∴y随x的增大而减小,
∴当x=200时,这批饮料销售总金额最大,
则650﹣x=650﹣200=450.
故该饮料厂生产甲种饮料200千克,乙种饮料450千克,才能使得这批饮料销售总金额最大.
28.(9分)已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC 边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
【解答】证明:(1)∵△ABC和△ADF都是等边三角形,
∴AF=AD,AB=AC,∠FAD=∠BAC=60°,
又∵∠FAB=∠FAD﹣∠BAD,∠DAC=∠BAC﹣∠BAD,
∴∠FAB=∠DAC,
在△AFB和△ADC中,
,
∴△AFB≌△ADC(SAS);
(2)由①得△AFB≌△ADC,
∴∠ABF=∠C=60°.
又∵∠BAC=∠C=60°,
∴∠ABF=∠BAC,
∴FB∥AC,
又∵BC∥EF,
∴四边形BCEF是平行四边形;
(3)成立,理由如下:
∵△ABC和△ADF都是等边三角形,
∴AF=AD,AB=AC,∠FAD=∠BAC=60°,
又∵∠FAB=∠BAC﹣∠FAE,∠DAC=∠FAD﹣∠FAE,
∴∠FAB=∠DAC,
在△AFB和△ADC中,
,
∴△AFB≌△ADC(SAS);
∴∠AFB=∠ADC.
又∵∠ADC+∠DAC=60°,∠EAF+∠DAC=60°,
∴∠ADC=∠EAF,
∴∠AFB=∠EAF,
∴BF∥AE,
又∵BC∥EF,
∴四边形BCEF是平行四边形.
同课章节目录
