19.2.2 平行四边形的判定(2)同步练习
文档属性
| 名称 | 19.2.2 平行四边形的判定(2)同步练习 |
|
|
| 格式 | docx | ||
| 文件大小 | 416.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-15 00:00:00 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
19.2.2 平行四边形的判定(2)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
三角形的中位线
(1)定义:连接三角形两边中点的线段叫做三角形的中位线.
(2)定理:三角形的两边中点连线平行于第三边,并且 等于第三边长的一半.
基础知识和能力拓展精练
一、选择题
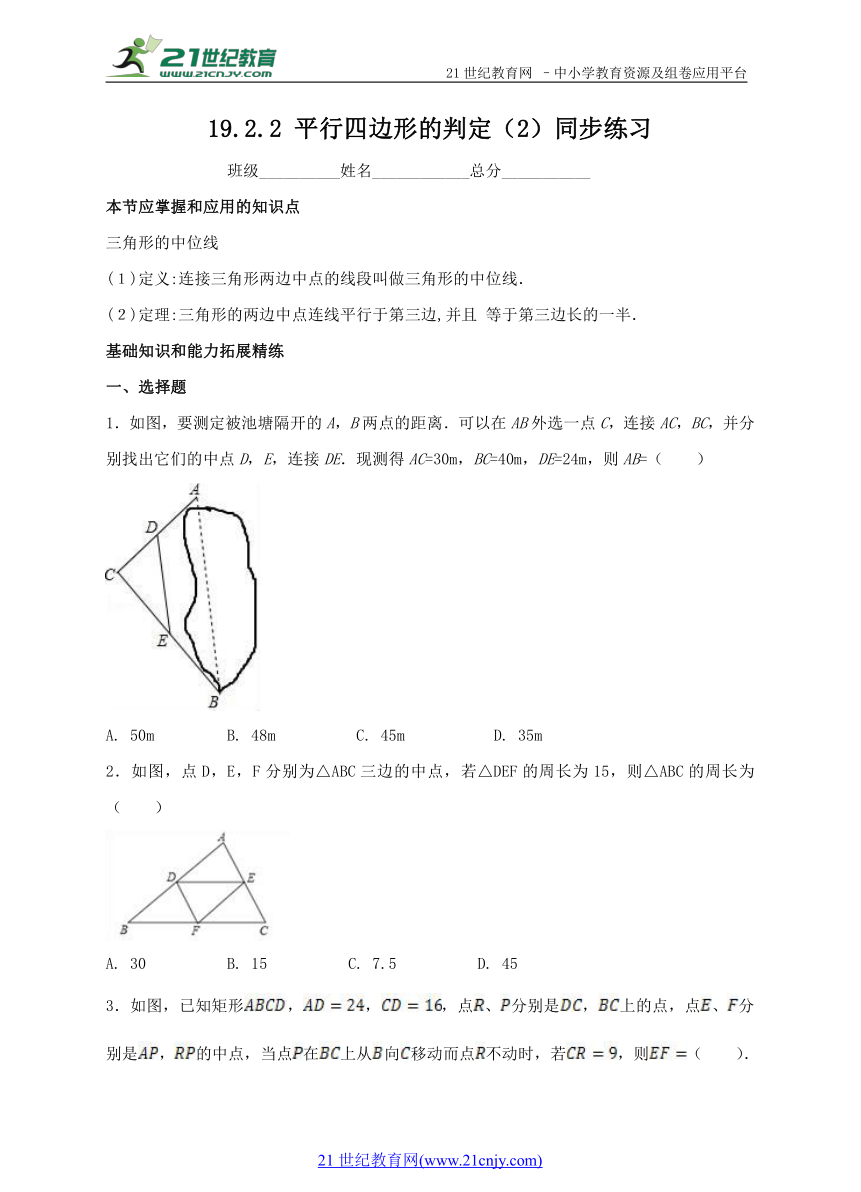
1.如图,要测定被池塘隔开的A,B两点的距离.可以在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接DE.现测得AC=30m,BC=40m,DE=24m,则AB=( )
A. 50m B. 48m C. 45m D. 35m
2.如图,点D,E,F分别为△ABC三边的中点,若△DEF的周长为15,则△ABC的周长为( )
A. 30 B. 15 C. 7.5 D. 45
3.如图,已知矩形,,,点、分别是,上的点,点、分别是,的中点,当点在上从向移动而点不动时,若,则( ).
A. B. C. D. 不能确定
4.如图,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点,若∠DAC=20°,∠ACB=66°,则∠FEG等于( )
A. 47° B. 46° C. 11.5° D. 23°
5.已知等腰三角形的两条中位线长分别为3和5,则此等腰三角形的周长为( )
A. 22 B. 26 C. 22或26 D. 23
6.如图所示,在△ABC中,M是BC的中点,AN平分∠BAC,BN⊥AN.若AB=14,AC=20,则MN的长为( )
A. 2 B. 2.5 C. 3 D. 3.5
7.如图,在△ABC中,AC=8,BC=12,AF交BC于F,E为AB的中点,CD平分∠ACB,且CD⊥AF,垂足为D,连接DE,则DE的长为( )
A. 2 B. C. 3 D. 4
8.已知△ABC的周长为1,连接其三边中点构成第二个三角形,再连接第二个三角形的中点构成第三个三角形,以此类推,则第2012个三角形的周长为( )
A. B. C. D.
9.如图,在四边形ABCD 中,AB=CD,M,N,P分别AD,BC,BD的中点,若∠MPN=130°,则∠NMP=( )
A. 25° B. 30° C. 35° D. 50°
10.如图,梯形ABCD中,AB∥CD,点E,F,G分别是BD,AC,DC的中点.已知两底之差是6,两腰之和是12,则△EFG的周长是( )
A. 8 B. 9 C. 10 D. 12
二、填空题
11.如图,△ABC中,D、E分别是AB、AC的中点,若BC=4cm,则DE=_____cm.
12.如图,在矩形ABCD中,M.N.分别是边AD,BC 的中点,点E、点F分别是线段BM,CN的中点,若AM=DM=6,AB=8,则四边形ENFM的周长为_______.
13.如图,在△ABC中,D,E分别是AB,AC的中点,F是BC延长线上的一点,FC=3,DF交CE于点G,且EG=CG,则BC=________.
14.如图,已知线段AB⊥CD,E,F分别是AD,CB的中点,且AB=16,CD=12,则EF的长是________.
15.如图,在△ABC中,AB=6,点D是AB的中点,过点D作DE∥BC,交AC于点,点M在DE上,且ME=DM.当AM⊥BM时,则BC的长为________.
16.如图,在四边形中,,,,点,分别在边,上,点,分别为,的中点,连接,则长度的最大值为__________.
三、解答题
17.已知△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足是E,F是BC的中点,试说明BD=2EF。
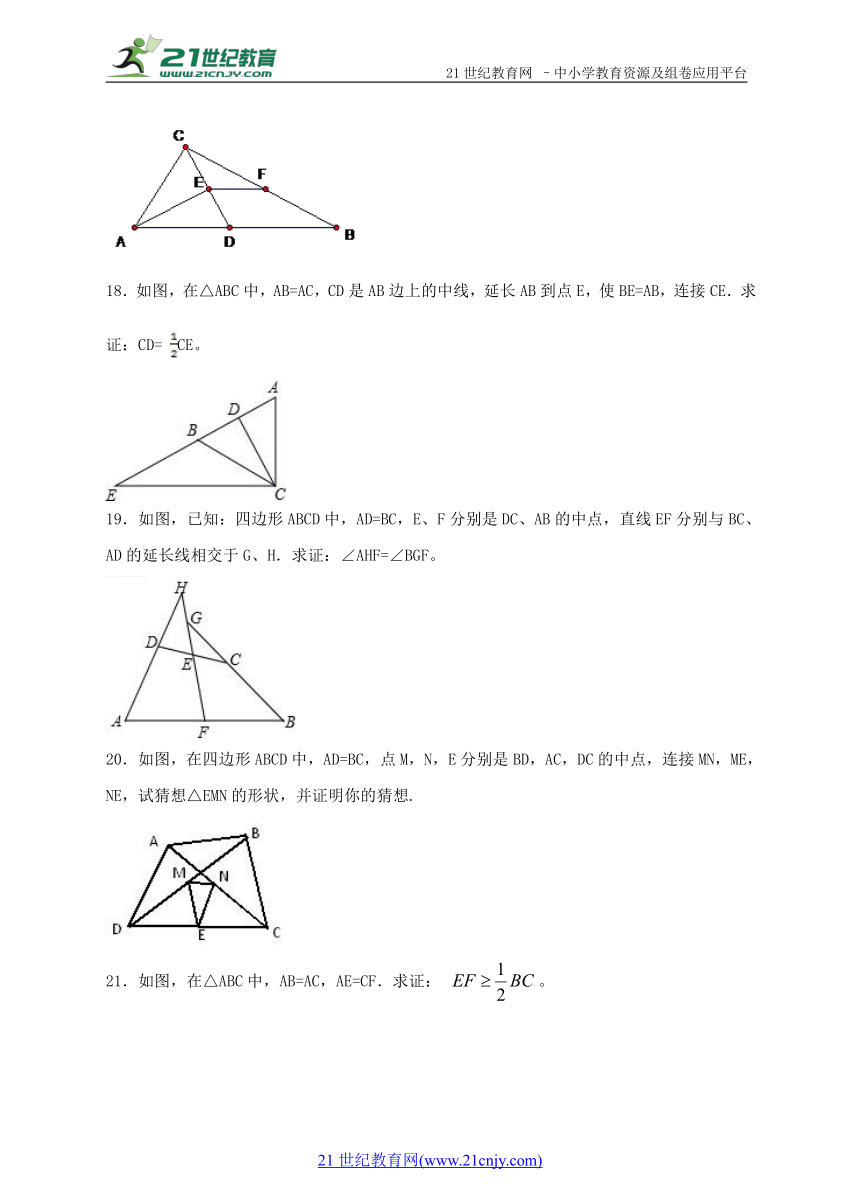
18.如图,在△ABC中,AB=AC,CD是AB边上的中线,延长AB到点E,使BE=AB,连接CE.求证:CD= CE。
19.如图,已知:四边形ABCD中,AD=BC,E、F分别是DC、AB的中点,直线EF分别与BC、AD的延长线相交于G、H.求证:∠AHF=∠BGF。
20.如图,在四边形ABCD中,AD=BC,点M,N,E分别是BD,AC,DC的中点,连接MN,ME,NE,试猜想△EMN的形状,并证明你的猜想.
21.如图,在△ABC中,AB=AC,AE=CF.求证: 。
22.如图,AD,BE分别是△ABC的中线和角平分线,AD⊥BE于点G,AD=BE=6,求AC的长.
23.如图,在中, ,点分别是的中点, 是延长线上的一点,且.
(1)求证: ;
(2)求证: .
参考答案
1.B
【解析】∵D是AC的中点,E是BC的中点,
∴DE是△ABC的中位线,
∴DE=AB,
∵DE=24m,
∴AB=2DE=48m,
故选B.
2.A
【解析】试题分析:根据三角形中位线的性质可得:AB=2EF,AC=2DF,BC=2DE,则△ABC的周长=2×(EF+DF+DE)=30,故选A.
3.B
【解析】连接.
∵,
,,
∴.
又∵中,
为中点,
为中点,
∴,
∴
故选B.
点睛:此题主要考查了勾股定理及三角形的中位线定理,熟练掌握勾股定理和三角形中位线定理是解答本题的关键.
4.D
【解析】∵AD=BC,E,F,G分别是AB,CD,AC的中点,
∴GF是△ACD的中位线,GE是△ACB的中位线,
又∵AD=BC,
∴GF=GE,∠FGC=∠DAC=20°,∠AGE=∠ACB=66°,
∴∠FGE=∠FGC+∠EGC=20°+(180°﹣66°)=134°,
∴∠FEG=(180°﹣∠FGE)=23°.
故选:D.
5.C
【解析】当与底边平行的中位线长为3时,底边长为6,腰长为10,三角形的周长为26;当与底边平行的中位线长为5时,底边长为10,腰长为6,三角形的周长为22,故选C.
6.C
【解析】如图,延长BN交AC于点D,因为AN平分∠BAC,BN⊥AN,所以BN=ND,AD=AB=14,又因为M是BC的中点,所以CD=2MN,因为CD=AC-AD=20-14=6,所以MN=3,故选C.
7.A
【解析】解:∵CD平分∠ACB,∴∠ACD=∠FCD.
在△ACD和△FCD中,∵∠ACD=∠FCD,CD=CD,∠ADC=∠FDC,∴△ACD≌△FCD,
∴FC=AC=8,AD=DF,∴BF=BC-CF=4.
∵E为AB的中点,AD=DF,∴DE是△ABF的中位线,∴DE=BF=2.故选A.
点睛:本题考查的是三角形中位线定理和三角形全等的判定和性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.
8.C
【解析】试题解析:∵连接△ABC三边中点构成第二个三角形,
∴新三角形的三边与原三角形的三边的比值为1:2,
∴它们相似,且相似比为1:2,
同理:第三个三角形与第二个三角形的相似比为1:2,
即第三个三角形与第一个三角形的相似比为:1:22,
以此类推:第2012个三角形与原三角形的相似比为1:22011,
∵周长为1,
∴第2012个三角形的周长为 1:22011.
故选C.
9.A
【解析】∵在四边形ABCD中,M、N、P分别是AD、BC、BD的中点,
∴PN,PM分别是△CDB与△DAB的中位线,
∴PM=AB,PN=DC,
∵AB=CD,
∴PM=PN,
∴△PMN是等腰三角形,
∵∠MPN=130°,
∴∠PMN=(180°-∠MPN)÷2=25°,
故选A.
10.B
【解析】如图,
找到AD的中点M,并连接EM
又∵E是BD的中点 ∴EM∥AB,EM=AB﹙三角形中位线的性质﹚
而AB∥CD ∴EM∥CD 又∵M是AD的中点
∴EM平分线段AC﹙平行线等分线段﹚ 而F是线段AC的中点
∴F在线段EM上 ∴FM是⊿ADC的中位线
∴FM=CD
∴EF=EM-FM=﹙AB-CD﹚=3
在⊿ADC中F是AC中点,G是CD中点 ∴FG=AD
同理得 EG=BC
∴FG+EG=﹙AD+BC﹚=6
∴⊿EFG的周长=6+3=9.
故选:B.
11.2
【解析】解:∵点D、E分别为△ABC的边AB、AC的中点,∴DE是△ABC的中位线,∴DE=BC.
又∵BC=4cm,∴DE=2cm.故答案为:2.
12.20
【解析】∵四边形ABCD为矩形,∴∠A=∠D=90°,在Rt△ABM中,AB=8,AM=6,由勾股定理得BM=10,同理CM=10,∵E、F分别是线段BM、CM的中点,BN=CN,∴EM=FM=5,∴EN,FN都是△BCM的中位线,∴EN=FN=5,∴四边形ENFM的周长为5+5+5+5=20,故答案为20.
13.6
【解析】∵D,E分别是AB和AC的中点,∴DE∥BC,DE=BC,在△GED和△GCF中, ,∴△GED≌△GCF,∴DE=CF=3,∴BC=2DE=6,故答案为6.
14.10
【解析】连接AC,取AC中点M,连接EM、FM,
∵E,F分别是AD,CB的中点,
∴EM//CD,EM=CD==6,
FM//AB,FM=AB==8,
∵AB⊥CD,∴∠1=90°,
∵FM//AB,∴∠2=∠1=90°,
∵EM//CD,∴∠3=∠2=90°,
∴EF==10,
故答案为:10.
【点睛】本题考查了三角形的中位线、勾股定理等知识,正确地添加辅助线是解题的关键.
15.8
【解析】根据直角三角形的性质(斜边上的中线等于斜边的一半),求出DM=AB=3,即可得到ME=1,根据题意求出DE=DM+ME=4,根据三角形中位线定理可得BC=2DE=8.
故答案为:8.
点睛:本题考查的是三角形的中位线定理的应用,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
16.3
【解析】连接,
∵点、分别为、中点,
∴,
∴最大时,最大,
∵与重合时最大,
,
∴的最大值是.
17.证明见解析.
【解析】试题分析:根据三角形的中位线定理,在三角形中准确应用,并且求证E为CD的中点,再求证EF为△BCD的中位线.
试题解析:
∵AD=AC,AE⊥CD,
∴CE=DE
∵CE=DE,F是BC的中点
∴BD=2EF
18.见解析
【解析】试题分析:作BF∥AC交EC于F,通过证明△FBC≌△DBC,得到CD=CF,根据三角形中位线定理得到CF=CE,等量代换得到答案.
试题解析:证明:作BF∥AC交EC于F.
∵BF∥AC,∴∠FBC=∠ACB.∵AB=AC,∴∠ABC=∠ACB,∴∠FBC=∠ABC.
∵BF∥AC,BE=AB,∴BF= AC,CF=CE.
∵CD是AB边上的中线,∴BD=AB,∴BF=BD.
在△FBC和△DBC中,∵BF=BD,∠FBC=∠DBC,BC=BC,∴△FBC≌△DBC,∴CD=CF,∴CD=CE.
点睛:本题考查的是三角形中位线定理、全等三角形的判定和性质以及等腰三角形的性质,正确作出辅助线、灵活运用定理是解题的关键.
19.见解析
【解析】试题分析:连接AC,作EM∥AD交AC于M,连接MF.根据中位线定理得到MF∥BC,且MF=BC,根据AD=BC得到EM=MF,∠MEF=∠MFE,根据平行线的性质,得到∠MEF=∠AHF,∠MFE=∠BGF.即可得到结论.
试题解析:证明:连接AC,作EM∥AD交AC于M,连接MF.如下图:
∵E是CD的中点,且EM∥AD,∴EM=AD,M是AC的中点.又∵F是AB的中点,∴MF∥BC,且MF=BC.
∵AD=BC,∴EM=MF,∴∠MEF=∠MFE.
∵EM∥AH,∴∠MEF=∠AHF.∵FM∥BG,∴∠MFE=∠BGF,∴∠AHF=∠BGF.
20.△EMN是等腰三角形.
【解析】试题分析:因为点M,N,E分别是BD,AC,DC的中点,所以ME,NE是三角形的中位线,根据三角形中位线的性质可得: ME=BC, NE=AD,因为BC=AD,所以ME=NE,根据等腰三角形的判定即可求解.
试题解析:猜想△EMN是等腰三角形,
因为M,E分别是BD,DC的中点,所以ME是△BDC的中位线.所以ME=BC.
同理,得NE=AD,
因为AD=BC,所以ME=NE,所以△EMN是等腰三角形.
21.证明见解析
【解析】过E作ED平行且等于BC,连接DF,DC,再由平行线的性质及全等三角形的性质,在△EFD中即可得出结论.
证明:过E作ED平行且等于BC,连接DF,DC,
如图所示,
∴BCDE是平行四边形,
∴DC平行且等于BE,
∴∠1=∠A,
∵AB=AC,AE=FC,
∴BE=AF=DC,
∴△AEF≌△CFD,
∴EF=DF,
在△EFD中,EF+DF>DE,
∴2EF>BC,即EF>BC,
当E、F为AB、AC中点时,EF=BC,
∴EF≥BC.
点睛:本题考查了平行四边形的判定与性质、三角形三边关系、全等三角形的判定与性质和三角形中位线定理.合理构造辅助线是解题的关键.
22.
【解析】试题分析:过D点作DF∥BE,交AC于点F.根据平行线分线段的性质,可得DF的长,然后根据勾股定理求出AF的长,再根据三角形的中位线的性质和等腰三角形的性质和判定求解即可.
试题解析:过D点作DF∥BE,交AC于点F.
∵AD是△ABC的中线,AD⊥BE
∴F为CE的中点,AD⊥DF.
∴DF是△BCE的中位线,∠ADF=90°.
∵AD=BE=6,
∴DF=BE=3
∴AF==3.
∵BE是△ABC的角平分线
∴∠ABG=∠DBG.
∵AD⊥BE
∴AG=DG,
即G为AD的中点.
∵BE∥DF,
∴E为AF的中点
∴AE=EF=CF=AF
∴AC=AF=×3= .
23.(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据三角形中位线定理可得DE=BC,再根据,从而可得DE=CF;
(2)利用SAS证明△BDE≌△ECF即可得.
试题解析:(1)∵点分别是的中点,
∴DE‖BC,且DE=BC,
∵,∴DE=CF;
(2)∵AD=BD=AB,AE=EC=AC,AB=AC,
∴BD=EC, AD=AE,
∴∠ADE=∠AED,
∴∠BDE=180°-∠ADE=180°-∠AED,
∵DE‖BC,∴∠AED=∠ACB,
∴∠ECF=180°-∠ACB ,∴∠BDE=∠ECF,
又由(1)得DE=CF, ∴△BDE≌△ECF(SAS),
∴BE=EF.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
19.2.2 平行四边形的判定(2)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
三角形的中位线
(1)定义:连接三角形两边中点的线段叫做三角形的中位线.
(2)定理:三角形的两边中点连线平行于第三边,并且 等于第三边长的一半.
基础知识和能力拓展精练
一、选择题
1.如图,要测定被池塘隔开的A,B两点的距离.可以在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接DE.现测得AC=30m,BC=40m,DE=24m,则AB=( )
A. 50m B. 48m C. 45m D. 35m
2.如图,点D,E,F分别为△ABC三边的中点,若△DEF的周长为15,则△ABC的周长为( )
A. 30 B. 15 C. 7.5 D. 45
3.如图,已知矩形,,,点、分别是,上的点,点、分别是,的中点,当点在上从向移动而点不动时,若,则( ).
A. B. C. D. 不能确定
4.如图,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点,若∠DAC=20°,∠ACB=66°,则∠FEG等于( )
A. 47° B. 46° C. 11.5° D. 23°
5.已知等腰三角形的两条中位线长分别为3和5,则此等腰三角形的周长为( )
A. 22 B. 26 C. 22或26 D. 23
6.如图所示,在△ABC中,M是BC的中点,AN平分∠BAC,BN⊥AN.若AB=14,AC=20,则MN的长为( )
A. 2 B. 2.5 C. 3 D. 3.5
7.如图,在△ABC中,AC=8,BC=12,AF交BC于F,E为AB的中点,CD平分∠ACB,且CD⊥AF,垂足为D,连接DE,则DE的长为( )
A. 2 B. C. 3 D. 4
8.已知△ABC的周长为1,连接其三边中点构成第二个三角形,再连接第二个三角形的中点构成第三个三角形,以此类推,则第2012个三角形的周长为( )
A. B. C. D.
9.如图,在四边形ABCD 中,AB=CD,M,N,P分别AD,BC,BD的中点,若∠MPN=130°,则∠NMP=( )
A. 25° B. 30° C. 35° D. 50°
10.如图,梯形ABCD中,AB∥CD,点E,F,G分别是BD,AC,DC的中点.已知两底之差是6,两腰之和是12,则△EFG的周长是( )
A. 8 B. 9 C. 10 D. 12
二、填空题
11.如图,△ABC中,D、E分别是AB、AC的中点,若BC=4cm,则DE=_____cm.
12.如图,在矩形ABCD中,M.N.分别是边AD,BC 的中点,点E、点F分别是线段BM,CN的中点,若AM=DM=6,AB=8,则四边形ENFM的周长为_______.
13.如图,在△ABC中,D,E分别是AB,AC的中点,F是BC延长线上的一点,FC=3,DF交CE于点G,且EG=CG,则BC=________.
14.如图,已知线段AB⊥CD,E,F分别是AD,CB的中点,且AB=16,CD=12,则EF的长是________.
15.如图,在△ABC中,AB=6,点D是AB的中点,过点D作DE∥BC,交AC于点,点M在DE上,且ME=DM.当AM⊥BM时,则BC的长为________.
16.如图,在四边形中,,,,点,分别在边,上,点,分别为,的中点,连接,则长度的最大值为__________.
三、解答题
17.已知△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足是E,F是BC的中点,试说明BD=2EF。
18.如图,在△ABC中,AB=AC,CD是AB边上的中线,延长AB到点E,使BE=AB,连接CE.求证:CD= CE。
19.如图,已知:四边形ABCD中,AD=BC,E、F分别是DC、AB的中点,直线EF分别与BC、AD的延长线相交于G、H.求证:∠AHF=∠BGF。
20.如图,在四边形ABCD中,AD=BC,点M,N,E分别是BD,AC,DC的中点,连接MN,ME,NE,试猜想△EMN的形状,并证明你的猜想.
21.如图,在△ABC中,AB=AC,AE=CF.求证: 。
22.如图,AD,BE分别是△ABC的中线和角平分线,AD⊥BE于点G,AD=BE=6,求AC的长.
23.如图,在中, ,点分别是的中点, 是延长线上的一点,且.
(1)求证: ;
(2)求证: .
参考答案
1.B
【解析】∵D是AC的中点,E是BC的中点,
∴DE是△ABC的中位线,
∴DE=AB,
∵DE=24m,
∴AB=2DE=48m,
故选B.
2.A
【解析】试题分析:根据三角形中位线的性质可得:AB=2EF,AC=2DF,BC=2DE,则△ABC的周长=2×(EF+DF+DE)=30,故选A.
3.B
【解析】连接.
∵,
,,
∴.
又∵中,
为中点,
为中点,
∴,
∴
故选B.
点睛:此题主要考查了勾股定理及三角形的中位线定理,熟练掌握勾股定理和三角形中位线定理是解答本题的关键.
4.D
【解析】∵AD=BC,E,F,G分别是AB,CD,AC的中点,
∴GF是△ACD的中位线,GE是△ACB的中位线,
又∵AD=BC,
∴GF=GE,∠FGC=∠DAC=20°,∠AGE=∠ACB=66°,
∴∠FGE=∠FGC+∠EGC=20°+(180°﹣66°)=134°,
∴∠FEG=(180°﹣∠FGE)=23°.
故选:D.
5.C
【解析】当与底边平行的中位线长为3时,底边长为6,腰长为10,三角形的周长为26;当与底边平行的中位线长为5时,底边长为10,腰长为6,三角形的周长为22,故选C.
6.C
【解析】如图,延长BN交AC于点D,因为AN平分∠BAC,BN⊥AN,所以BN=ND,AD=AB=14,又因为M是BC的中点,所以CD=2MN,因为CD=AC-AD=20-14=6,所以MN=3,故选C.
7.A
【解析】解:∵CD平分∠ACB,∴∠ACD=∠FCD.
在△ACD和△FCD中,∵∠ACD=∠FCD,CD=CD,∠ADC=∠FDC,∴△ACD≌△FCD,
∴FC=AC=8,AD=DF,∴BF=BC-CF=4.
∵E为AB的中点,AD=DF,∴DE是△ABF的中位线,∴DE=BF=2.故选A.
点睛:本题考查的是三角形中位线定理和三角形全等的判定和性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.
8.C
【解析】试题解析:∵连接△ABC三边中点构成第二个三角形,
∴新三角形的三边与原三角形的三边的比值为1:2,
∴它们相似,且相似比为1:2,
同理:第三个三角形与第二个三角形的相似比为1:2,
即第三个三角形与第一个三角形的相似比为:1:22,
以此类推:第2012个三角形与原三角形的相似比为1:22011,
∵周长为1,
∴第2012个三角形的周长为 1:22011.
故选C.
9.A
【解析】∵在四边形ABCD中,M、N、P分别是AD、BC、BD的中点,
∴PN,PM分别是△CDB与△DAB的中位线,
∴PM=AB,PN=DC,
∵AB=CD,
∴PM=PN,
∴△PMN是等腰三角形,
∵∠MPN=130°,
∴∠PMN=(180°-∠MPN)÷2=25°,
故选A.
10.B
【解析】如图,
找到AD的中点M,并连接EM
又∵E是BD的中点 ∴EM∥AB,EM=AB﹙三角形中位线的性质﹚
而AB∥CD ∴EM∥CD 又∵M是AD的中点
∴EM平分线段AC﹙平行线等分线段﹚ 而F是线段AC的中点
∴F在线段EM上 ∴FM是⊿ADC的中位线
∴FM=CD
∴EF=EM-FM=﹙AB-CD﹚=3
在⊿ADC中F是AC中点,G是CD中点 ∴FG=AD
同理得 EG=BC
∴FG+EG=﹙AD+BC﹚=6
∴⊿EFG的周长=6+3=9.
故选:B.
11.2
【解析】解:∵点D、E分别为△ABC的边AB、AC的中点,∴DE是△ABC的中位线,∴DE=BC.
又∵BC=4cm,∴DE=2cm.故答案为:2.
12.20
【解析】∵四边形ABCD为矩形,∴∠A=∠D=90°,在Rt△ABM中,AB=8,AM=6,由勾股定理得BM=10,同理CM=10,∵E、F分别是线段BM、CM的中点,BN=CN,∴EM=FM=5,∴EN,FN都是△BCM的中位线,∴EN=FN=5,∴四边形ENFM的周长为5+5+5+5=20,故答案为20.
13.6
【解析】∵D,E分别是AB和AC的中点,∴DE∥BC,DE=BC,在△GED和△GCF中, ,∴△GED≌△GCF,∴DE=CF=3,∴BC=2DE=6,故答案为6.
14.10
【解析】连接AC,取AC中点M,连接EM、FM,
∵E,F分别是AD,CB的中点,
∴EM//CD,EM=CD==6,
FM//AB,FM=AB==8,
∵AB⊥CD,∴∠1=90°,
∵FM//AB,∴∠2=∠1=90°,
∵EM//CD,∴∠3=∠2=90°,
∴EF==10,
故答案为:10.
【点睛】本题考查了三角形的中位线、勾股定理等知识,正确地添加辅助线是解题的关键.
15.8
【解析】根据直角三角形的性质(斜边上的中线等于斜边的一半),求出DM=AB=3,即可得到ME=1,根据题意求出DE=DM+ME=4,根据三角形中位线定理可得BC=2DE=8.
故答案为:8.
点睛:本题考查的是三角形的中位线定理的应用,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
16.3
【解析】连接,
∵点、分别为、中点,
∴,
∴最大时,最大,
∵与重合时最大,
,
∴的最大值是.
17.证明见解析.
【解析】试题分析:根据三角形的中位线定理,在三角形中准确应用,并且求证E为CD的中点,再求证EF为△BCD的中位线.
试题解析:
∵AD=AC,AE⊥CD,
∴CE=DE
∵CE=DE,F是BC的中点
∴BD=2EF
18.见解析
【解析】试题分析:作BF∥AC交EC于F,通过证明△FBC≌△DBC,得到CD=CF,根据三角形中位线定理得到CF=CE,等量代换得到答案.
试题解析:证明:作BF∥AC交EC于F.
∵BF∥AC,∴∠FBC=∠ACB.∵AB=AC,∴∠ABC=∠ACB,∴∠FBC=∠ABC.
∵BF∥AC,BE=AB,∴BF= AC,CF=CE.
∵CD是AB边上的中线,∴BD=AB,∴BF=BD.
在△FBC和△DBC中,∵BF=BD,∠FBC=∠DBC,BC=BC,∴△FBC≌△DBC,∴CD=CF,∴CD=CE.
点睛:本题考查的是三角形中位线定理、全等三角形的判定和性质以及等腰三角形的性质,正确作出辅助线、灵活运用定理是解题的关键.
19.见解析
【解析】试题分析:连接AC,作EM∥AD交AC于M,连接MF.根据中位线定理得到MF∥BC,且MF=BC,根据AD=BC得到EM=MF,∠MEF=∠MFE,根据平行线的性质,得到∠MEF=∠AHF,∠MFE=∠BGF.即可得到结论.
试题解析:证明:连接AC,作EM∥AD交AC于M,连接MF.如下图:
∵E是CD的中点,且EM∥AD,∴EM=AD,M是AC的中点.又∵F是AB的中点,∴MF∥BC,且MF=BC.
∵AD=BC,∴EM=MF,∴∠MEF=∠MFE.
∵EM∥AH,∴∠MEF=∠AHF.∵FM∥BG,∴∠MFE=∠BGF,∴∠AHF=∠BGF.
20.△EMN是等腰三角形.
【解析】试题分析:因为点M,N,E分别是BD,AC,DC的中点,所以ME,NE是三角形的中位线,根据三角形中位线的性质可得: ME=BC, NE=AD,因为BC=AD,所以ME=NE,根据等腰三角形的判定即可求解.
试题解析:猜想△EMN是等腰三角形,
因为M,E分别是BD,DC的中点,所以ME是△BDC的中位线.所以ME=BC.
同理,得NE=AD,
因为AD=BC,所以ME=NE,所以△EMN是等腰三角形.
21.证明见解析
【解析】过E作ED平行且等于BC,连接DF,DC,再由平行线的性质及全等三角形的性质,在△EFD中即可得出结论.
证明:过E作ED平行且等于BC,连接DF,DC,
如图所示,
∴BCDE是平行四边形,
∴DC平行且等于BE,
∴∠1=∠A,
∵AB=AC,AE=FC,
∴BE=AF=DC,
∴△AEF≌△CFD,
∴EF=DF,
在△EFD中,EF+DF>DE,
∴2EF>BC,即EF>BC,
当E、F为AB、AC中点时,EF=BC,
∴EF≥BC.
点睛:本题考查了平行四边形的判定与性质、三角形三边关系、全等三角形的判定与性质和三角形中位线定理.合理构造辅助线是解题的关键.
22.
【解析】试题分析:过D点作DF∥BE,交AC于点F.根据平行线分线段的性质,可得DF的长,然后根据勾股定理求出AF的长,再根据三角形的中位线的性质和等腰三角形的性质和判定求解即可.
试题解析:过D点作DF∥BE,交AC于点F.
∵AD是△ABC的中线,AD⊥BE
∴F为CE的中点,AD⊥DF.
∴DF是△BCE的中位线,∠ADF=90°.
∵AD=BE=6,
∴DF=BE=3
∴AF==3.
∵BE是△ABC的角平分线
∴∠ABG=∠DBG.
∵AD⊥BE
∴AG=DG,
即G为AD的中点.
∵BE∥DF,
∴E为AF的中点
∴AE=EF=CF=AF
∴AC=AF=×3= .
23.(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据三角形中位线定理可得DE=BC,再根据,从而可得DE=CF;
(2)利用SAS证明△BDE≌△ECF即可得.
试题解析:(1)∵点分别是的中点,
∴DE‖BC,且DE=BC,
∵,∴DE=CF;
(2)∵AD=BD=AB,AE=EC=AC,AB=AC,
∴BD=EC, AD=AE,
∴∠ADE=∠AED,
∴∠BDE=180°-∠ADE=180°-∠AED,
∵DE‖BC,∴∠AED=∠ACB,
∴∠ECF=180°-∠ACB ,∴∠BDE=∠ECF,
又由(1)得DE=CF, ∴△BDE≌△ECF(SAS),
∴BE=EF.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
