2018高中数学(文)黄金100题系列第17题+幂函数
文档属性
| 名称 | 2018高中数学(文)黄金100题系列第17题+幂函数 |

|
|
| 格式 | zip | ||
| 文件大小 | 746.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-15 00:00:00 | ||
图片预览




文档简介
第17题幂函数
I.题源探究·黄金母题
【例】已知幂函数的图象过点(2,),试求出此函数的解析式,并作出图像,判断奇偶性、单调性.
【解析】设=,则,解得,
所以=,定义域为,是非奇非偶函数,
∵,∴在是减函数,图像如下:
精彩解读
【试题来源】人教版A版必修1第82页复习参考题A组第10题
【母题评析】本题考查幂函数的解析式、图象、奇偶性、单调性,是基础题.是高考重要考点之一.
【思路方法】求幂函数的解析式常用待定系数法,研究幂函数的定义域、值域、奇偶性、单调性常用图像法,在研究函数性质时,一定要先求定义域,注意幂函数与指数函数的区别,注意不同的幂函数定义域、图像、性质可能不同.
II.考场精彩·真题回放
【例1】【2014高考浙江卷】在同一坐标系中,函数,的图象可能是()
【答案】D
【解析】对A,没有幂函数的图象,不符合题目要求;对B,中,中,不符合题意;对C,中,中,不符合题意;对D,中,中,符合题意;故选D.
【例2】【2014上海卷】若,则满足的取值范围是.
【答案】
【解析】根据幂函数的性质,由于,所以当时,当时,,因此的解集为.
【命题意图】本类题通常主要考查幂函数的图像与性质的应用.
【考试方向】这类试题在考查题型上,通常基本以选择题或填空题的形式出现,难度较小,往往与不等式、函数性质等数学知识相结合,考查幂函数的定义、图像与性质.
【难点中心】幂函数因幂指数不同其定义域、值域、图像、奇偶性、单调性也不同,故解决幂函数问题,要根据解析式,首项求函数的定义域,根据幂指数确定其图像与性质,,熟记不同范围幂指数所对函数的图像与性质,是解题要熟练处理与幂函数有关的问题的关键.
III.理论基础·解题原理
考点一幂函数的概念与表示
一般地,形如(R)的函数称为幂孙函数,其中是自变量,是常数.
考点二幂函数的图像与性质
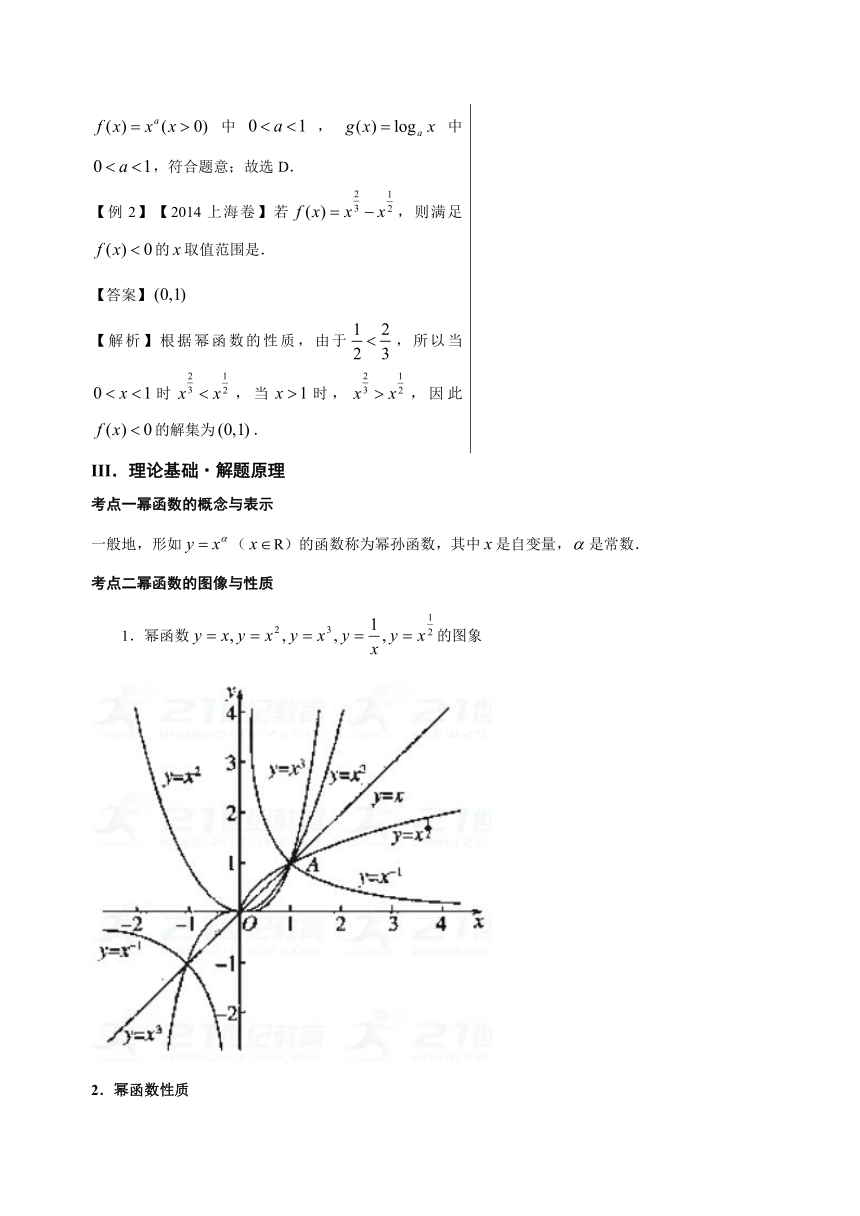
1.幂函数的图象
2.幂函数性质
定义域
值域
奇偶性
奇函数
偶函数
奇函数
非奇非偶函数
奇函数
单调性
增函数
减函数,增函数
增函数
增函数
减函数,增函数
定点
,
IV.题型攻略·深度挖掘
【考试方向】
这类试题在考查题型上,通常基本以选择题或填空题的形式出现,难度较小,往往与函数、不等式等数学知识结合考查幂函数的图像与性质.
【技能方法】
1.幂函数,其中为常数,其本质特征是以幂的底为自变量,指数为常数,这是判断一个函数是否是幂函数的重要依据和唯一标准.
2.在上,幂函数中指数越大,函数图象越靠近x轴(简记为“指大图低”),在(1,+∞)上,幂函数中指数越大,函数图象越远离x轴.
3.幂函数的图象一定会出现在第一象限内,一定不会出现在第四象限内,至于是否出现在第二、三象限内,要看函数的奇偶性;幂函数的图象最多只能同时出现在两个象限内;如果幂函数的图象与坐标轴相交,则交点一定是原点.
【易错指导】
(1)在掌握幂函数时,注意幂函数系数为1,底数为自变量,指数为常数这一特征;
(2)注意幂函数的指数定义域、值域、单调性、对称性与幂函数的幂指数有关;
(3)注意幂函数与指数函数区别.
V.举一反三·触类旁通
考向1 幂函数的概念与表示
【例1】【2018河南三门峡模拟】已知幂函数的图象关于轴对称,且在上是减函数,则的值为( )
A. B.1 C.2 D.1或2
【答案】B
【例2】【2018宁夏银川模拟】已知幂函数的图象过点,则()
A.B.C.D.与大小无法判定
【答案】A
【解析】设,则,,即,在上是减函数,所以.故选A.
【跟踪练习】
1.【2018黑龙江哈尔滨模拟】若幂函数的图象不过原点,则的取值是()
A.B.C.D.
【答案】D
2.【2018山西45校第一次联考】幂函数在其图象上点处的切线方程为()
A. B. C. D.
【答案】A
【解析】将点代入得,解得,故幂函数为,因为,故切线方程为,即,故选A.
3.【2018广西钦州模拟】使代数式(|x|-1有意义的x的取值范围是()
A.|x|≥1 B.-11 D.x∈R,且x≠±1
【答案】D
【解析】,选D.
考向2 幂函数的图像
【例3】【2018湖北鄂东南省级示范高中高三上学期期中联考】若幂函数与在第一象限的图象如图所示,则与的取值情况为()
A. B. C. D.
【答案】D
【例4】【2018浙江诸暨模拟】下图中曲线是幂函数在第一象限内的图象,已知p分别为,中的一个,则相应于曲线C1、C2、C3、C4的p值依次是()
A.-2,,,2B.,-2,2,C.2,,,-2D.2,,-2,
【答案】C
【解析】做直线,与四个函数图象从上到下的交点依次记为,而,从而相应于曲线的n依次为2,,,-2,故选C.
【例5】【2018山东济南模拟】已知函数在区间上的最大值是,则的取值范围是.
【答案】
【解析】,作出函数图象,如图所示,因为函数在上的最大值为,又所以,即.
【跟踪练习】
1.函数的图象是()
A. B. C. D.
【答案】B
点评:幂函数是重要的基本初等函数模型之一.学习幂函数重点是掌握幂函数的图形特征,即图象语言,熟记幂函数的图象、性质,把握幂函数的关键点(1,1)和利用直线y=x来刻画其它幂函数在第一象限的凸向.
2.【2018湖北黄冈9月质量检测】函数(,)与的图象如图,则下列不等式一定成立的是()
A. B. C. D.
【答案】D
3.【2017河南周口市上学期期末调研】已知指数函数(且)的图像恒过定点,若定点在幂函数的图像上,则幂函数的图像是()
A BC D
【答案】A
【解析】令,即时,,即指数函数(且)的图象恒过定点,又因为定点在幂函数的图象上,所以,即,解得,则在定义域上单调递增,故选A.
考向3 幂函数性质
【例6】【2017江西赣州模拟】幂函数的图象经过点,则是()
A.偶函数,且在上是增函数 B.偶函数,且在上是减函数
C.奇函数,且在上是增函数 D.非奇非偶函数,且在上是增函数
【答案】C
【解析】设幂函数为,代入点,解得,所以,可知函数是奇函数,且在上是增函数,故选C.
【例7】【2017河南新乡二模】设,,,则的大小关系是()
A. B. C. D.
【答案】B
【例8】【2018内蒙古集宁一中模拟】设,则使得函数的定义域为R且为奇函数的所有的值为()
A.-1,3 B.-1,1 C.1,3 D.-1,1,3
【答案】C
【解析】由题意,当时尽管也是奇函数,但定义域是,应选答案C .
【跟踪练习】
1.设>0且≠1 ,则“函数=在R上是减函数”,是“函数=在R上是增函数”的()
.充分不必要条件.必要不充分条件.充分必要条件.既不充分也不必要条件
【答案】A.
【解析】p:“函数=在R上是减函数”等价于;q:“函数=在R上是增函数”等价于,即且≠1,故p是q成立的充分不必要条件.故选.
2.【2018东北师大附中模拟】已知幂函数的图象关于轴对称,则下列选项正确的是()
A. B. C. D.
【答案】B
【解析】由于幂函数的图象关于轴对称,可知为偶函数,所以,即.则有,,所以,故选B.
3.【2017浙江省余姚中学二模】已知幂函数过点,则满足的实数的取值范围是.
【答案】
考向4 幂函数的综合应用
【例9】【2018山东滕州三中模拟】已知幂函数f(x)=xa的图象经过点(2,4),则下列判断中不正确的是( )
A.函数图象经过点(﹣1,1)
B.当x∈[﹣1,2]时,函数f(x)的值域是[0,4]
C.函数满足f(x)+f(﹣x)=0
D.函数f(x)的单调减区间为(﹣∞,0]
【答案】C
【解析】由题意可知,,所以,所以,A对,x∈[﹣1,2]时,函数f(x)的值域是[0,4],B对.在(﹣∞,0]上单调递减,D对,偶函数,C错,选C.
【例10】【2018山东济宁微山县二中高三上学期第一次月考】下列命题正确的是()
A.的图像是一条直线
B.幂函数的图像都经过点
C.若幂函数是奇函数,则是增函数
D.幂函数的图像不可能出现在第四象限
【答案】D
【解析】对于,函数的图象是一条直线除去点,故错误;对于,幂函数的图象都经过点,当指数大于时,都经过点,当指数小于时,不经过点,故错误;对于,若幂函数是奇函数,且时,是定义域上的增函数,时,在及上均为减函数,故错误;由幂函数的性质,幂函数的图象一定过第一象限,不可能出现在第四象限,正确,故选D.
【方法点睛】本题主要通过对多个命题真假的判断,主要综合考查幂函数的单调性、幂函数的奇偶性、幂函数的图象与性质,属于难题.这种题型综合性较强,也是高考的命题热点,同学们往往因为某一处知识点掌握不好而导致“全盘皆输”,因此做这类题目更要细心、多读题,尽量挖掘出题目中的隐含条件,另外,要注意从简单的自己已经掌握的知识点入手,然后集中精力突破较难的命题.
【例11】【2017河南濮阳模拟】当时,下列函数中图象全在直线下方的增函数是()
A. B. C. D.
【答案】A
【例12】【2017河南息县一中高三下学期第三次阶段测试】若集合,则()
A. B. C. D.
【答案】C
【解析】因为,所以,故选C.
【跟踪练习】
1.设函数,若=4,则实数=
A.-4或-2 B.-4或2 C.-2或4 D.-2或2
【答案】B
【解析】∵=4 ∴或,解得=-4或=2,故选B.
2.已知函数,若关于x的方程有两个不同的实根,则实数k的取值范围是________.
【答案】(0,1)
3.若<,则实数a的取值范围是_____________.
【答案】
【解析】不等式(a+1)<(3-2a)等价于a+1>3-2a>0或3-2a解得a<-1或4.已知幂函数在上单调递增,函数.
(1)求的值;
(2)当时,记的值域分别为集合,若,求实数的取值范围.
【答案】(1)(2)
【解析】(1)由幂函数的定义可得,解出的值,注意验证(2)当时,单调递增,易得的值域,由即可求实数的取值范围.
试题解析:(1)依题意得:,解得或.
当时,在上单调递减,与题设矛盾,舍去.∴.
(2)由(1)可知,当时,单调递增,∴,∵,∴,∴.故实数的取值范围是.
I.题源探究·黄金母题
【例】已知幂函数的图象过点(2,),试求出此函数的解析式,并作出图像,判断奇偶性、单调性.
【解析】设=,则,解得,
所以=,定义域为,是非奇非偶函数,
∵,∴在是减函数,图像如下:
精彩解读
【试题来源】人教版A版必修1第82页复习参考题A组第10题
【母题评析】本题考查幂函数的解析式、图象、奇偶性、单调性,是基础题.是高考重要考点之一.
【思路方法】求幂函数的解析式常用待定系数法,研究幂函数的定义域、值域、奇偶性、单调性常用图像法,在研究函数性质时,一定要先求定义域,注意幂函数与指数函数的区别,注意不同的幂函数定义域、图像、性质可能不同.
II.考场精彩·真题回放
【例1】【2014高考浙江卷】在同一坐标系中,函数,的图象可能是()
【答案】D
【解析】对A,没有幂函数的图象,不符合题目要求;对B,中,中,不符合题意;对C,中,中,不符合题意;对D,中,中,符合题意;故选D.
【例2】【2014上海卷】若,则满足的取值范围是.
【答案】
【解析】根据幂函数的性质,由于,所以当时,当时,,因此的解集为.
【命题意图】本类题通常主要考查幂函数的图像与性质的应用.
【考试方向】这类试题在考查题型上,通常基本以选择题或填空题的形式出现,难度较小,往往与不等式、函数性质等数学知识相结合,考查幂函数的定义、图像与性质.
【难点中心】幂函数因幂指数不同其定义域、值域、图像、奇偶性、单调性也不同,故解决幂函数问题,要根据解析式,首项求函数的定义域,根据幂指数确定其图像与性质,,熟记不同范围幂指数所对函数的图像与性质,是解题要熟练处理与幂函数有关的问题的关键.
III.理论基础·解题原理
考点一幂函数的概念与表示
一般地,形如(R)的函数称为幂孙函数,其中是自变量,是常数.
考点二幂函数的图像与性质
1.幂函数的图象
2.幂函数性质
定义域
值域
奇偶性
奇函数
偶函数
奇函数
非奇非偶函数
奇函数
单调性
增函数
减函数,增函数
增函数
增函数
减函数,增函数
定点
,
IV.题型攻略·深度挖掘
【考试方向】
这类试题在考查题型上,通常基本以选择题或填空题的形式出现,难度较小,往往与函数、不等式等数学知识结合考查幂函数的图像与性质.
【技能方法】
1.幂函数,其中为常数,其本质特征是以幂的底为自变量,指数为常数,这是判断一个函数是否是幂函数的重要依据和唯一标准.
2.在上,幂函数中指数越大,函数图象越靠近x轴(简记为“指大图低”),在(1,+∞)上,幂函数中指数越大,函数图象越远离x轴.
3.幂函数的图象一定会出现在第一象限内,一定不会出现在第四象限内,至于是否出现在第二、三象限内,要看函数的奇偶性;幂函数的图象最多只能同时出现在两个象限内;如果幂函数的图象与坐标轴相交,则交点一定是原点.
【易错指导】
(1)在掌握幂函数时,注意幂函数系数为1,底数为自变量,指数为常数这一特征;
(2)注意幂函数的指数定义域、值域、单调性、对称性与幂函数的幂指数有关;
(3)注意幂函数与指数函数区别.
V.举一反三·触类旁通
考向1 幂函数的概念与表示
【例1】【2018河南三门峡模拟】已知幂函数的图象关于轴对称,且在上是减函数,则的值为( )
A. B.1 C.2 D.1或2
【答案】B
【例2】【2018宁夏银川模拟】已知幂函数的图象过点,则()
A.B.C.D.与大小无法判定
【答案】A
【解析】设,则,,即,在上是减函数,所以.故选A.
【跟踪练习】
1.【2018黑龙江哈尔滨模拟】若幂函数的图象不过原点,则的取值是()
A.B.C.D.
【答案】D
2.【2018山西45校第一次联考】幂函数在其图象上点处的切线方程为()
A. B. C. D.
【答案】A
【解析】将点代入得,解得,故幂函数为,因为,故切线方程为,即,故选A.
3.【2018广西钦州模拟】使代数式(|x|-1有意义的x的取值范围是()
A.|x|≥1 B.-1
【答案】D
【解析】,选D.
考向2 幂函数的图像
【例3】【2018湖北鄂东南省级示范高中高三上学期期中联考】若幂函数与在第一象限的图象如图所示,则与的取值情况为()
A. B. C. D.
【答案】D
【例4】【2018浙江诸暨模拟】下图中曲线是幂函数在第一象限内的图象,已知p分别为,中的一个,则相应于曲线C1、C2、C3、C4的p值依次是()
A.-2,,,2B.,-2,2,C.2,,,-2D.2,,-2,
【答案】C
【解析】做直线,与四个函数图象从上到下的交点依次记为,而,从而相应于曲线的n依次为2,,,-2,故选C.
【例5】【2018山东济南模拟】已知函数在区间上的最大值是,则的取值范围是.
【答案】
【解析】,作出函数图象,如图所示,因为函数在上的最大值为,又所以,即.
【跟踪练习】
1.函数的图象是()
A. B. C. D.
【答案】B
点评:幂函数是重要的基本初等函数模型之一.学习幂函数重点是掌握幂函数的图形特征,即图象语言,熟记幂函数的图象、性质,把握幂函数的关键点(1,1)和利用直线y=x来刻画其它幂函数在第一象限的凸向.
2.【2018湖北黄冈9月质量检测】函数(,)与的图象如图,则下列不等式一定成立的是()
A. B. C. D.
【答案】D
3.【2017河南周口市上学期期末调研】已知指数函数(且)的图像恒过定点,若定点在幂函数的图像上,则幂函数的图像是()
A BC D
【答案】A
【解析】令,即时,,即指数函数(且)的图象恒过定点,又因为定点在幂函数的图象上,所以,即,解得,则在定义域上单调递增,故选A.
考向3 幂函数性质
【例6】【2017江西赣州模拟】幂函数的图象经过点,则是()
A.偶函数,且在上是增函数 B.偶函数,且在上是减函数
C.奇函数,且在上是增函数 D.非奇非偶函数,且在上是增函数
【答案】C
【解析】设幂函数为,代入点,解得,所以,可知函数是奇函数,且在上是增函数,故选C.
【例7】【2017河南新乡二模】设,,,则的大小关系是()
A. B. C. D.
【答案】B
【例8】【2018内蒙古集宁一中模拟】设,则使得函数的定义域为R且为奇函数的所有的值为()
A.-1,3 B.-1,1 C.1,3 D.-1,1,3
【答案】C
【解析】由题意,当时尽管也是奇函数,但定义域是,应选答案C .
【跟踪练习】
1.设>0且≠1 ,则“函数=在R上是减函数”,是“函数=在R上是增函数”的()
.充分不必要条件.必要不充分条件.充分必要条件.既不充分也不必要条件
【答案】A.
【解析】p:“函数=在R上是减函数”等价于;q:“函数=在R上是增函数”等价于,即且≠1,故p是q成立的充分不必要条件.故选.
2.【2018东北师大附中模拟】已知幂函数的图象关于轴对称,则下列选项正确的是()
A. B. C. D.
【答案】B
【解析】由于幂函数的图象关于轴对称,可知为偶函数,所以,即.则有,,所以,故选B.
3.【2017浙江省余姚中学二模】已知幂函数过点,则满足的实数的取值范围是.
【答案】
考向4 幂函数的综合应用
【例9】【2018山东滕州三中模拟】已知幂函数f(x)=xa的图象经过点(2,4),则下列判断中不正确的是( )
A.函数图象经过点(﹣1,1)
B.当x∈[﹣1,2]时,函数f(x)的值域是[0,4]
C.函数满足f(x)+f(﹣x)=0
D.函数f(x)的单调减区间为(﹣∞,0]
【答案】C
【解析】由题意可知,,所以,所以,A对,x∈[﹣1,2]时,函数f(x)的值域是[0,4],B对.在(﹣∞,0]上单调递减,D对,偶函数,C错,选C.
【例10】【2018山东济宁微山县二中高三上学期第一次月考】下列命题正确的是()
A.的图像是一条直线
B.幂函数的图像都经过点
C.若幂函数是奇函数,则是增函数
D.幂函数的图像不可能出现在第四象限
【答案】D
【解析】对于,函数的图象是一条直线除去点,故错误;对于,幂函数的图象都经过点,当指数大于时,都经过点,当指数小于时,不经过点,故错误;对于,若幂函数是奇函数,且时,是定义域上的增函数,时,在及上均为减函数,故错误;由幂函数的性质,幂函数的图象一定过第一象限,不可能出现在第四象限,正确,故选D.
【方法点睛】本题主要通过对多个命题真假的判断,主要综合考查幂函数的单调性、幂函数的奇偶性、幂函数的图象与性质,属于难题.这种题型综合性较强,也是高考的命题热点,同学们往往因为某一处知识点掌握不好而导致“全盘皆输”,因此做这类题目更要细心、多读题,尽量挖掘出题目中的隐含条件,另外,要注意从简单的自己已经掌握的知识点入手,然后集中精力突破较难的命题.
【例11】【2017河南濮阳模拟】当时,下列函数中图象全在直线下方的增函数是()
A. B. C. D.
【答案】A
【例12】【2017河南息县一中高三下学期第三次阶段测试】若集合,则()
A. B. C. D.
【答案】C
【解析】因为,所以,故选C.
【跟踪练习】
1.设函数,若=4,则实数=
A.-4或-2 B.-4或2 C.-2或4 D.-2或2
【答案】B
【解析】∵=4 ∴或,解得=-4或=2,故选B.
2.已知函数,若关于x的方程有两个不同的实根,则实数k的取值范围是________.
【答案】(0,1)
3.若<,则实数a的取值范围是_____________.
【答案】
【解析】不等式(a+1)<(3-2a)等价于a+1>3-2a>0或3-2a
(1)求的值;
(2)当时,记的值域分别为集合,若,求实数的取值范围.
【答案】(1)(2)
【解析】(1)由幂函数的定义可得,解出的值,注意验证(2)当时,单调递增,易得的值域,由即可求实数的取值范围.
试题解析:(1)依题意得:,解得或.
当时,在上单调递减,与题设矛盾,舍去.∴.
(2)由(1)可知,当时,单调递增,∴,∵,∴,∴.故实数的取值范围是.
同课章节目录
