人教版小学四年级下册数学总复习(59张PPT)
文档属性
| 名称 | 人教版小学四年级下册数学总复习(59张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-16 22:20:39 | ||
图片预览









文档简介
(共60张PPT)
知识点一:四则混合运算
知识点二:位置与方向
知识点三:运算定律与简便计算
知识点四:小数的意义和性质
知识点五:小数的加法和减法
知识点六:三 角 形
知识点七: 统 计
知识点八:数学广角
四年级《数学》下册各单元目录
总复习
知识点一:四则运算
1、加法、减法、乘法和除法统称 。
2、在没有括号的算式里,如果只有加、减法或者只有乘、除法,都要按 的顺序计算。
3、在没有括号的算式里,有乘、除法和加、减法、要 。
4、算式有括号, 。
从左往右
先算乘除法,再算加减法
要先算括号里面的
四则运算
1、“0”不能做除数; 字母表示:a÷0 ?
2、一个数加上0还得原数; 字母表示:a+0= ?
3、一个数减去0还得原数; 字母表示:a-0= ?
4、被减数等于减数,差是0; 字母表示:a-a= ?
5、一个数和0相乘,仍得0; 字母表示:a×0= ?
6、0除以任何非0的数还得0。 字母表示:0÷a(a≠0)= ?
有关“0”的运算
练习一
45.36-18.72+5.68
46×25÷5×3
232÷(32+26)×13
(1444-81×16)÷74
1、同一个物体的位置对于不同的观测点来说,所描述的位置是( )的。
不同
2、上海在北京的南偏东30°的方向上,也可以说上海在北京的( )的方向上。
东偏南60°
3、上海在北京的南偏东30°的方向上,那么北京在上海的( )的方向上。
北偏西30°
4、确定一个点的位置要根据( )和( )两个条件。
方向
距离
知识点二:位置与方向
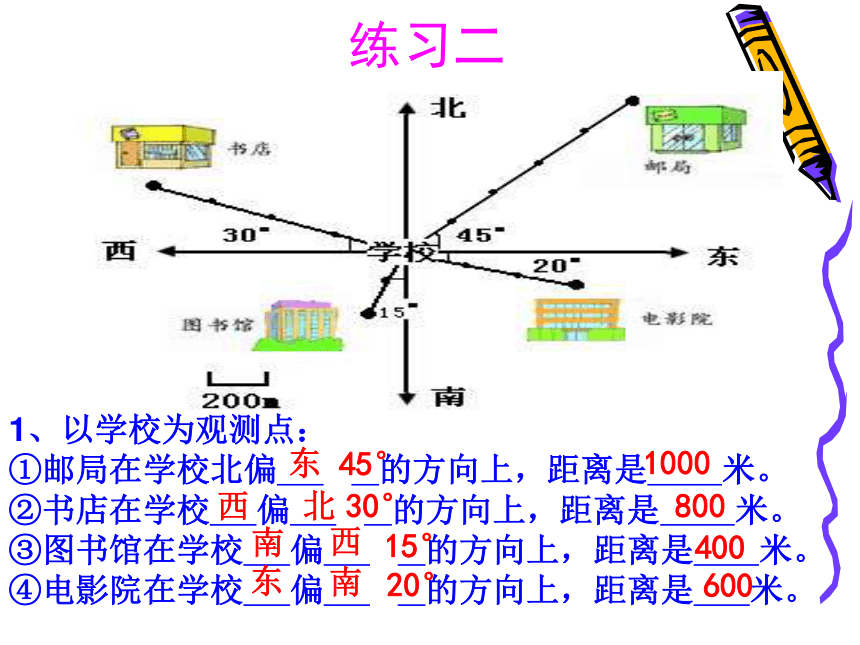
1、以学校为观测点:
①邮局在学校北偏 的方向上,距离是 米。
②书店在学校 偏 的方向上,距离是 米。
③图书馆在学校 偏 的方向上,距离是 米。
④电影院在学校 偏 的方向上,距离是 米。
东
45°
1000
西
北
30°
800
南
西
15°
400
东
南
20°
600
练习二
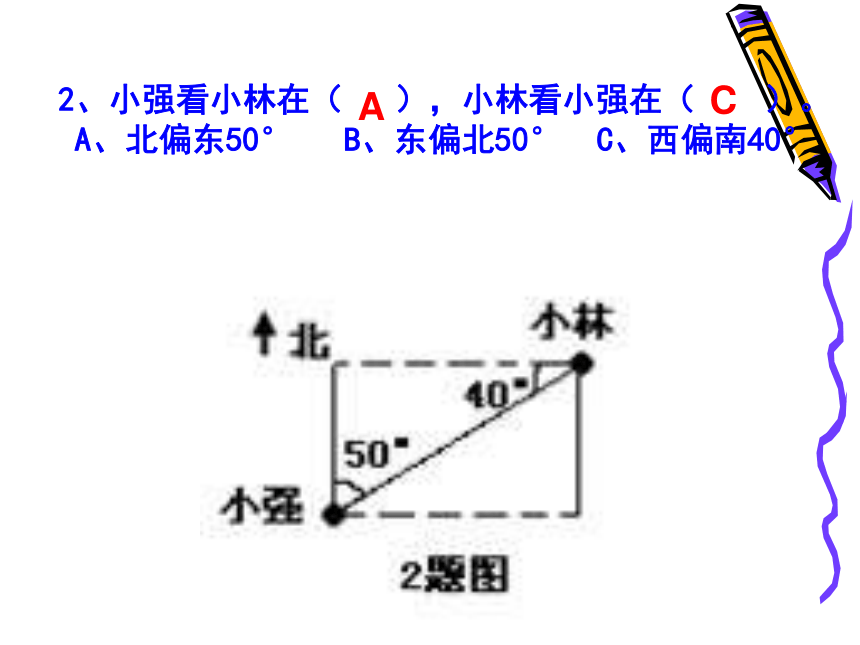
2、小强看小林在( ),小林看小强在( )。
A、北偏东50° B、东偏北50° C、西偏南40°
A
C
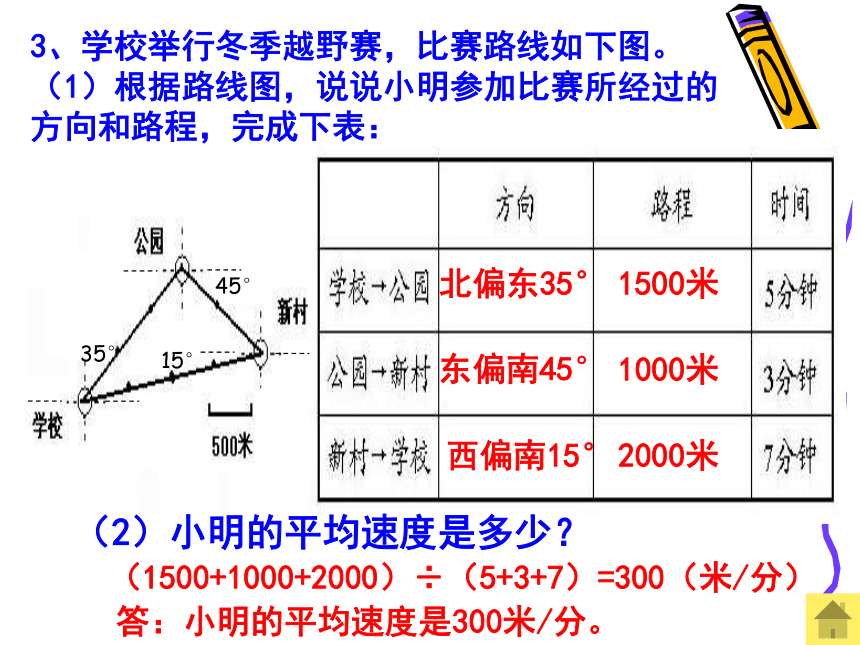
(2)小明的平均速度是多少?
北偏东35°
1500米
东偏南45°
1000米
西偏南15°
2000米
(1500+1000+2000)÷(5+3+7)=300(米/分)
答:小明的平均速度是300米/分。
3、学校举行冬季越野赛,比赛路线如下图。
(1)根据路线图,说说小明参加比赛所经过的方向和路程,完成下表:
35°
45°
15°
知识点三:运算定律
1.加法交换律:a+b=b+a
50+98+50 =
2.加法结合律:(a+b) +c=a+(b+c)
488+40+60=
3.乘法交换律:a×b=b×a
25×56×4=
4.乘法结合律:(a×b)×c=a×(b×c)
99×125×8 =
简便计算一
含有加法交换律与结合律的简便计算:
65+28+35+72
含有乘法交换律与结合律的简便计算:
25×125×4×8
5.乘法分配律:(a+b)×c=a×c+b×c
拓 展:(a-b)×c=a×c-b×c
简算例子:
①分解式 ②合并式
25×(40+4) 135×12—135×2
简便计算二
③特殊1: 99×256+256
④特殊2: 45×102
⑤特殊3: 99×26
⑥特殊4: 35×8+35×6—4×35
6.连减:a-b-c=a-(b+c)
简便运算例子:
528—65—35 528—(150+128)
7.连除:a÷b÷c=a÷(b×c)
简便运算例子:
3200÷25÷4
一、常见乘法计算:
25×4=100 125×8=1000
二、加法交换律简算例子: 三、加法结合律简算例子:
50+98+50 488+40+60
=50+50+98 =488+(40+60)
=100+98 =488+100
=198 =588
四、乘法交换律简算例子: 五、乘法结合律简算例子:
25×56×4 99×125×8
=25×4×56 =99×(125×8)
=100×56 =99×1000
=5600 =99000
练习三(例题)
练习三(例题)
乘法分配律简算例子:
一、分解式 二、合并式
25×(40+4) 135×12—135×2
=25×40+25×4 =135×(12—2)
=1000+100 =135×10
=1100 =1350
练习三(例题)
连续减法简便运算例子:
528—65—35 528—89—128 528—150+128)
=528—(65+35) =528—128—89 =528—128—150
=528—100 =400—89 =400—150
=428 =311 =250
连续除法简便运算例子:
3200÷25÷4
=3200÷(25×4)
=3200÷100
=32
其它简便运算例子:
256—58+44 250÷8×4
=256+44—58 =250×4÷8
=300—58 =1000÷8
=242 =125
知识点四:小数的意义和性质
1、小数的数位顺序表
整数部分 小
数
点 小数部分
数
位 … · …
计
数
单
位 … …
万位
千位
百位
十位
个位
十分位
百分位
千分位
万分位
万
千
百
十
一(个)
十分之一
百分之一
万分之一
千分之一
填一填。
1、在小数中,小数部分在小数点的( ),整数部分在小数点的( )。
2、小数点右边第一位是( ),它的计数单位是( ),第二位是( ),它的计数单位是( )。
3、0.9的计数单位是( ),它有( )个这样的计数单位,0.600的计数单位是( ),它有( )个这样的计数单位。
右边
左边
十分位
十分之一
百分位
百分之一
0.1
9
0.001
600
练习四
6、 5.234的小数点右边第一位是( ),
表示( )个( );小数点右边第二位是( ) ,表示( )个( );小数点右边第三位是( )。表示( )个( );
7、0.008是一个( )位小数,计数单位是( );112.3是一个( )位小数,计数单位是( )。
2
2
0.1
3
3
0.01
4
4
0.001
三
千分之一
一
十分之一
8、每相邻两个计数单位间的进率是( )。
9、小数部分数位的最高位是( )。整数部分的最低位是( )。个位和十分位的进率是( )。
①23.06这个小数,整数部分的最高位是( )位,小数部分的最低位是( )位,0在( )位上 。
②0.825是由8个( )、2个( )和5个( )组成的。
十分位
个位
10
10
十
百分
十分
十分之一
百分之一
千分之一
1.8
5.63
12.378
读小数的时候,整数部分按照整数的读法来读(整数部分是0的读作“零”),小数点读作“点”,小数部分顺次读出每一个数位上的数字。
读作:一点八
2、小数的读法:
读作:五点六三
读作:十二点三七八
①有一个数,百位、十位和十分位上都是7,个位和百分位上都是0,这个数写作( )。
②由5个1,4个0.1和7个0.01组成的数是( )。
③4个十分之一、8个百分之一、5个千分之一组成的数
是( )。
770.70
5.47
0.485
5
0.4
0.07
0.4
0.08
0.005
3、小数的写法:先写整数部分(按照原来的写法),再写小数点,再写小数部分:写小数部分,小数部分要依次写出每个数字,而且有几个0就写几个0。
(1)在 里填上“<”、“>”或“=”。
2.3 3.3
<
0.93 0.94
<
0.057 0.053
>
0.99 1
<
6.9 6.8
>
4.50 4.5
=
4、小数的大小比较:(1) 先比较整数部分;(2)如果整数部分相同,就比较十分位;(3)十分位相同,就比较百分位;(4)以此类推,直到比较出大小。
5、小数的性质:小数的末尾添上“0”或者去掉“0”,小数的大小不变。
0.70= 0.080= .
105.0900= 12.000= .
(2)化简下面的小数。
0.2= 4.08= 3= .
(3)不改变数的大小,把下面各数写成三位数。
0.7
0.08
105.09
12
0.200
4.080
3.000
6、小数点的移动
小数点向右移:
移动一位,小数就扩大到原数的10倍;
移动两位,小数就扩大到原数的100倍;
移动三位,小数就扩大到原数的1000倍;
… …
小数点向左移:
移动一位,小数就缩小10倍,即小数就缩小到原数的 ;
移动两位,小数就缩小100倍,即小数就缩小到原数的 ;
移动三位,小数就缩小1000倍,即小数就缩小到原数的 ;
… …
32.8
去掉小数点原数 ( )
扩大100倍是 ( )
扩大( )倍是 32800
缩小10倍是 ( )
把小数点移到3的左边,原数( )
缩小( )倍是0.0328
3280
3.28
1000
1000
扩大10倍
缩小100倍
填一填
1.把2.32的小数点向右移动两位,它就扩大到原数的( )倍。
3.把3.75扩大100倍,小数点 向( )移动( )位,是( ).
6.把0.073的小数点向( )移动( )位,原数就变成730。
5.把140的小数点向( )移动( )位,原数变成0.14。
2.把2.32的小数点向左移动两位,它就缩小到原数的( )。
4.把3.75缩小到它的 ,小数点 向( )移动( )位,是( )
100
1
100
100
1
右
两
左
两
三
左
四
右
375
0.0375
7、生活中常用的单位:
质量:1吨=1000千克 1千克=1000克
长度:1千米=1000米 1分米=10厘米 1厘米=10毫米
1分米=100毫米 1米=10分米=100厘米
面积:1平方米= 100平方分米
1平方分米=100平方厘米
1平方千米=100公顷 1公顷=10000平方米
人民币: 1元=10角 1角=10分 1元=100分
高级单位
低级单位
×进率
÷进率
50厘米=( )米 1.2米=( )分米
0.8平方千米=( )公顷
600平方米=( )公顷
15分=( )元 8.09吨=( )千克
0.5
12
80
0.06
0.15
8090
52米4厘米=( )米
1吨25千克=( )吨
2.37米=( )厘米
52.04
237
1.025
填一填。
1米6厘米=( )米 9千克9克( )千克
5米7分米=( )分米
1.98千米=( )千米( )米
2.06吨=( )吨( )千克
7元3分=( )元
1.06
9009
57
1
980
2
60
7.03
8、小数的近似数(用“四舍五入”的方法):
(1)保留整数,表示精确到个位,要看十分位,把它四舍五入。
(2)保留一位小数,表示精确到十分位,要看小数的第二位,把它四舍五入。
(3)保留两位小数,表示精确到百分位,要看小数的第三位,把它四舍五入。
注意:在表示近似数时,小数末尾的0不能去掉。
求下面小数的近似数。
(1) 0.2563 12.0049 (精确到百分位)
(2) 7.816 13.974 (省略十分位后面的尾数)
(3) 1.234 25.519 (精确到个位)
≈0.26
≈12.00
≈7.8
≈14.0
≈1
≈26
(4)一个三位小数约等于0.36,它可能是多少?
其中最大是( ),最小是( )。
0.364
0.355
(5)改写成用“万”做单位的数,并保留一位小数
204500 = ( )≈( )
7100=( )≈( )
39800=( )≈( )
(6)改写成用“亿”作单位的数,并精确到百分位。
743200000=( )≈( )
53900000=( )≈( )
499500000=( )≈( )
20.45万
20.5万
0.71万
0.7万
3.98万
4.0万
7.432亿
7.43亿
0.539亿
0.54亿
4.995亿
5.00亿
知识点五:小数的加法和减法
1、小数的加、减法要注意:小数点要对齐也就是把数位对齐,得数的末尾有0,一般要把0去掉。
2、整数的运算定律(以及简便的方法)在小数运算中同样适用。
练习五
5.6+2.7+4.4
9.14-1.43-4.57
9.5+4.85-6.13
77+2.7+2.3+25
10.75+0.4-9.86
51.27-8.66-1.34
1、怎样简便就怎样算。
知识点六:三角形
1、由三条线段围成的图形(每相邻两条线段的端点
相连)叫做三角形。
2、从三角形的一个顶点到它的对边做一条垂线,顶
点到垂足之间的线段叫做三角形的高,这条边叫
做三角形的底。三角形只有3条高。
3、三角形具有稳定性。
4、三角形任意两边之和大于第三边。
5、三个角都是锐角的三角形叫做锐角三角形。
6、有一个角是直角的三角形叫做直角三角形。
7、有一个角是钝角的三角形叫做钝角三角形。
8、每个三角形都最少有两个锐角;每个三角形都最
多有1个直角;每个三角形都最多有1个钝角。
9、两条边相等的三角形叫做等腰三角形。
10、三条边都相等的三角形叫等边三角形,也叫正三
角形。
11、等边三角形是特殊的等腰三角形
12、三角形的内角和是180°。
13、四边形的内角和是360°
14、用2个相同的三角形可以拼成一个平行四边形。
15、用2个相同的直角三角形可以拼成一个平行四边
形、一个长方形、一个大三角形。
16、用2个相同的等腰的直角的三角形可以拼成一个
平行四边形、一个正方形。一个大的等腰的直角
的三角形。
一、填空。
1、锐角三角形中有( )个锐角;直角三角形中有( )个直角, ( )个锐角;钝角三角形中有( )个钝角, ( )个锐角。
2、直角三角形的三个角中,最大的一个角是( )度,另外两个角都是( )角。
3、做房屋的金字架是运用了三角形( )的特性。
4、一个等腰三角形的一个底角是55度,它的顶角是( )度,还可以说,它是一个( )三角形。
5、三个完全一样的三角形可以拼成一个( )形,至少要( )个完全一样的三角形才能拼成一个正方形。
6、按照三角形中边的不同,三角形可以分为( )和( )这两类特殊的三角形。
练习六
3
1
2
1
2
90
锐
稳定
70
锐角
梯
2
等腰三角形
等边三角形
1、一个三角形最少有( )个锐角,最多有( )个直角。
二、选择
A、1 1 B、2 1 C、3 2
2、一个三角形中,最多有( )个钝角。
A、3 B、2 C、1
3、一个直角三角形,已知一个角是25度,则第三个角是( )度。
A、75° B、65° C、165°
4、正三角形每个角都是( )度。
A、90° B、100° C、60°
5、一个三角形,已知两个角分别是50°和70°,则第三个角是( )度。
A、60° B、90° C、80°
B
C
B
C
A
三、解决问题
1、张明做一个等边三角形的风筝,风筝的周长是270厘米。这个风筝每条边的长是多少厘米?
2、一条红领巾的一个底角是30度,它的顶角是多少度?
3、边长为12厘米的正方形铁丝框,拆开后围成一个最大的等边三角形。这个等边三角形的边长是多少厘米?
4、一块等腰三角形绿地,它的周长是185米,一条腰长是52米,它的底边长多少米?
270÷3=90(厘米)
答:这个风筝每条边的长是90厘米。
30×2=60°
180°-60°=120°
答:它的顶角是120°。
答:这个等边三角形的边长是16厘米。
12×4=48(厘米)
48÷3=16(厘米)
52×2=104(米)
185-104=81(米)
答:它的底边长81米。
5、一个三角形的两条边分别是7cm和4cm,第三条边的长可能是多少?(答案取整数)
7-4=3(cm)
7+4=11(cm)
第三条边大于3厘米且小于11厘米。
答:第三条边的长可能是4厘米、5厘米、6厘米、7厘米、8厘米、9厘米、 10厘米。
条形统计图优点:直观地反映数量的多少。
折线统计图优点:既可以反映数量的多少,又能反映数量的增减变化。
折线统计图中,变化趋势指:上升或者下降。
知识点七 :统 计
(1)( )年沙尘暴总天数最多,( )年沙尘暴总天数最少。
(2)13年以来沙尘暴总天数的整体趋势为( )。
(3)从图上你还能得到哪些信息?你有什么好的建议?
1991年
1998年
沙尘暴天数有所下降,但每年仍持续半个月之久 。
2090
2162
2210
2253
2366
2476
2622
答:呈上升趋势。
要表示凉鞋销售的变化情况,用哪种统计图比较好呢?
根据统计图回答下列问题:
①说一说销售量的变化情况, 想一想变化的原因。
②如果每月卖出60双凉鞋便能收回成本,那么有哪几个月盈利?哪几个月亏本?哪几个月不亏不盈?
③你认为去年销售量的统计对以后鞋店确定进货数量有什么帮助?
2005年凉鞋销售量统计图
30
20
60
70
140
230
350
320
180
80
30
10
0
知识点八 :数学广角
(一)植树问题:
1、 两端要栽:间隔数=总长÷间距; 总长=间距×间隔数;
棵数=间隔数+1; 间隔数=棵数-1
2、 两端不栽:间隔数=总长÷间距; 总长=间距×间隔数;
棵数=间隔数-1; 间隔数=棵数+1
(二)锯木问题: 段数=次数+1; 次数=段数-1
总时间=每次时间×次数
(三)方阵问题:
最外层的数目是:边长×4-4或者是(边长-1)×4
整个方阵的总数目是:边长×边长
(四)封闭的图形(例如围成一个圆形、椭圆形):
总长÷间距=间隔数;棵数=间隔数
两端栽
两端不栽
锯木问题
方阵问题
封闭图形
1、园林工人要在长400米的路的一侧栽树,每隔8米栽一棵,两端都要栽。一共要栽多少棵树?
400÷8=50(棵)
50+1=51(棵)
答:一共要栽51棵。
练习八
2、在一条全长180米的街道两旁安装路灯,
(两端都要安装),每隔6米安一座。一共
要安装多少座路灯?
180÷6=30(个)
30+1=31(座)
31×2=62 (座)
答:一共要安装62座路灯。
3、园林工人沿公路一侧植树 ,每隔 6米种一棵,一共种了36棵。从第1棵到最后一棵的距离有多远?
36-1=35( 个)
6×35=210(米)
答:从第1棵到最后一棵的距离有210米远。
4、两棵大树之间相距250米,园林部门计划在两棵大树中间补栽小树,使每两棵小树之间的距离是10米,一共要补栽多少棵小树?
250÷10=25(个)
25-1=24(棵)
答:一共要补栽24棵小树。
5、永兴小学教学楼与实验楼相距120米,要在道路两侧栽树,每两棵树之间的距离是8米。这条路上一共有多少棵树?
120÷8=15(个)
15-1=14(棵)
14×2=28(棵)
答:一共有28棵树。
大营希望小学
6、 一根木头长10米,要把它平均分成5段。每锯下一段需要8分钟,锯完一共要花多少分钟?
大营希望小学
5-1=4(次)
4×8=32(分)
答:锯完一共要花32分钟。
大营希望小学
7、酒店里的大钟4时敲4下,6秒敲完,10时敲响10下,需要多长时间?
大营希望小学
4-1=3(个)
6÷3=2(秒)
10-1=9(个)
9×2=18(秒)
答:需要18秒。
8、小明从1楼到3楼需走36级台阶,小明从1楼到6楼需走多少级台阶
36÷(3-1)=18(级)
18×(6-1)=90(级)
答:小明从1楼到6楼需
走90级台阶。
8、在正方形的水池边摆花盆,使每边都有5盆花,可以怎样摆?一共需要多少盆花?
第一种摆法:每边5盆,顶角不摆。
5×4=20(盆)
答:一共需要20盆。
第二种摆法:每边5盆,顶角要摆。
(5-1)×4=16(盆)
答:一共需要16盆。
或 5×4-4=16(盆)
9、24名学生围成一个正方形做游戏,每边人数相等,四个顶点都有人,每边各有多少名学生?
24÷4=6(人)
6+1=7(人)
答:每边各有7名学生。
圆形花坛的一周全长50米,如果沿着这一圈每隔2米摆放一盆花,一共需要多少盆花?
10、
50÷2=25(盆)
答:一共需要25盆。
11、
150÷15=10(盏)
答:一共需要10盏灯。
知识点一:四则混合运算
知识点二:位置与方向
知识点三:运算定律与简便计算
知识点四:小数的意义和性质
知识点五:小数的加法和减法
知识点六:三 角 形
知识点七: 统 计
知识点八:数学广角
四年级《数学》下册各单元目录
总复习
知识点一:四则运算
1、加法、减法、乘法和除法统称 。
2、在没有括号的算式里,如果只有加、减法或者只有乘、除法,都要按 的顺序计算。
3、在没有括号的算式里,有乘、除法和加、减法、要 。
4、算式有括号, 。
从左往右
先算乘除法,再算加减法
要先算括号里面的
四则运算
1、“0”不能做除数; 字母表示:a÷0 ?
2、一个数加上0还得原数; 字母表示:a+0= ?
3、一个数减去0还得原数; 字母表示:a-0= ?
4、被减数等于减数,差是0; 字母表示:a-a= ?
5、一个数和0相乘,仍得0; 字母表示:a×0= ?
6、0除以任何非0的数还得0。 字母表示:0÷a(a≠0)= ?
有关“0”的运算
练习一
45.36-18.72+5.68
46×25÷5×3
232÷(32+26)×13
(1444-81×16)÷74
1、同一个物体的位置对于不同的观测点来说,所描述的位置是( )的。
不同
2、上海在北京的南偏东30°的方向上,也可以说上海在北京的( )的方向上。
东偏南60°
3、上海在北京的南偏东30°的方向上,那么北京在上海的( )的方向上。
北偏西30°
4、确定一个点的位置要根据( )和( )两个条件。
方向
距离
知识点二:位置与方向
1、以学校为观测点:
①邮局在学校北偏 的方向上,距离是 米。
②书店在学校 偏 的方向上,距离是 米。
③图书馆在学校 偏 的方向上,距离是 米。
④电影院在学校 偏 的方向上,距离是 米。
东
45°
1000
西
北
30°
800
南
西
15°
400
东
南
20°
600
练习二
2、小强看小林在( ),小林看小强在( )。
A、北偏东50° B、东偏北50° C、西偏南40°
A
C
(2)小明的平均速度是多少?
北偏东35°
1500米
东偏南45°
1000米
西偏南15°
2000米
(1500+1000+2000)÷(5+3+7)=300(米/分)
答:小明的平均速度是300米/分。
3、学校举行冬季越野赛,比赛路线如下图。
(1)根据路线图,说说小明参加比赛所经过的方向和路程,完成下表:
35°
45°
15°
知识点三:运算定律
1.加法交换律:a+b=b+a
50+98+50 =
2.加法结合律:(a+b) +c=a+(b+c)
488+40+60=
3.乘法交换律:a×b=b×a
25×56×4=
4.乘法结合律:(a×b)×c=a×(b×c)
99×125×8 =
简便计算一
含有加法交换律与结合律的简便计算:
65+28+35+72
含有乘法交换律与结合律的简便计算:
25×125×4×8
5.乘法分配律:(a+b)×c=a×c+b×c
拓 展:(a-b)×c=a×c-b×c
简算例子:
①分解式 ②合并式
25×(40+4) 135×12—135×2
简便计算二
③特殊1: 99×256+256
④特殊2: 45×102
⑤特殊3: 99×26
⑥特殊4: 35×8+35×6—4×35
6.连减:a-b-c=a-(b+c)
简便运算例子:
528—65—35 528—(150+128)
7.连除:a÷b÷c=a÷(b×c)
简便运算例子:
3200÷25÷4
一、常见乘法计算:
25×4=100 125×8=1000
二、加法交换律简算例子: 三、加法结合律简算例子:
50+98+50 488+40+60
=50+50+98 =488+(40+60)
=100+98 =488+100
=198 =588
四、乘法交换律简算例子: 五、乘法结合律简算例子:
25×56×4 99×125×8
=25×4×56 =99×(125×8)
=100×56 =99×1000
=5600 =99000
练习三(例题)
练习三(例题)
乘法分配律简算例子:
一、分解式 二、合并式
25×(40+4) 135×12—135×2
=25×40+25×4 =135×(12—2)
=1000+100 =135×10
=1100 =1350
练习三(例题)
连续减法简便运算例子:
528—65—35 528—89—128 528—150+128)
=528—(65+35) =528—128—89 =528—128—150
=528—100 =400—89 =400—150
=428 =311 =250
连续除法简便运算例子:
3200÷25÷4
=3200÷(25×4)
=3200÷100
=32
其它简便运算例子:
256—58+44 250÷8×4
=256+44—58 =250×4÷8
=300—58 =1000÷8
=242 =125
知识点四:小数的意义和性质
1、小数的数位顺序表
整数部分 小
数
点 小数部分
数
位 … · …
计
数
单
位 … …
万位
千位
百位
十位
个位
十分位
百分位
千分位
万分位
万
千
百
十
一(个)
十分之一
百分之一
万分之一
千分之一
填一填。
1、在小数中,小数部分在小数点的( ),整数部分在小数点的( )。
2、小数点右边第一位是( ),它的计数单位是( ),第二位是( ),它的计数单位是( )。
3、0.9的计数单位是( ),它有( )个这样的计数单位,0.600的计数单位是( ),它有( )个这样的计数单位。
右边
左边
十分位
十分之一
百分位
百分之一
0.1
9
0.001
600
练习四
6、 5.234的小数点右边第一位是( ),
表示( )个( );小数点右边第二位是( ) ,表示( )个( );小数点右边第三位是( )。表示( )个( );
7、0.008是一个( )位小数,计数单位是( );112.3是一个( )位小数,计数单位是( )。
2
2
0.1
3
3
0.01
4
4
0.001
三
千分之一
一
十分之一
8、每相邻两个计数单位间的进率是( )。
9、小数部分数位的最高位是( )。整数部分的最低位是( )。个位和十分位的进率是( )。
①23.06这个小数,整数部分的最高位是( )位,小数部分的最低位是( )位,0在( )位上 。
②0.825是由8个( )、2个( )和5个( )组成的。
十分位
个位
10
10
十
百分
十分
十分之一
百分之一
千分之一
1.8
5.63
12.378
读小数的时候,整数部分按照整数的读法来读(整数部分是0的读作“零”),小数点读作“点”,小数部分顺次读出每一个数位上的数字。
读作:一点八
2、小数的读法:
读作:五点六三
读作:十二点三七八
①有一个数,百位、十位和十分位上都是7,个位和百分位上都是0,这个数写作( )。
②由5个1,4个0.1和7个0.01组成的数是( )。
③4个十分之一、8个百分之一、5个千分之一组成的数
是( )。
770.70
5.47
0.485
5
0.4
0.07
0.4
0.08
0.005
3、小数的写法:先写整数部分(按照原来的写法),再写小数点,再写小数部分:写小数部分,小数部分要依次写出每个数字,而且有几个0就写几个0。
(1)在 里填上“<”、“>”或“=”。
2.3 3.3
<
0.93 0.94
<
0.057 0.053
>
0.99 1
<
6.9 6.8
>
4.50 4.5
=
4、小数的大小比较:(1) 先比较整数部分;(2)如果整数部分相同,就比较十分位;(3)十分位相同,就比较百分位;(4)以此类推,直到比较出大小。
5、小数的性质:小数的末尾添上“0”或者去掉“0”,小数的大小不变。
0.70= 0.080= .
105.0900= 12.000= .
(2)化简下面的小数。
0.2= 4.08= 3= .
(3)不改变数的大小,把下面各数写成三位数。
0.7
0.08
105.09
12
0.200
4.080
3.000
6、小数点的移动
小数点向右移:
移动一位,小数就扩大到原数的10倍;
移动两位,小数就扩大到原数的100倍;
移动三位,小数就扩大到原数的1000倍;
… …
小数点向左移:
移动一位,小数就缩小10倍,即小数就缩小到原数的 ;
移动两位,小数就缩小100倍,即小数就缩小到原数的 ;
移动三位,小数就缩小1000倍,即小数就缩小到原数的 ;
… …
32.8
去掉小数点原数 ( )
扩大100倍是 ( )
扩大( )倍是 32800
缩小10倍是 ( )
把小数点移到3的左边,原数( )
缩小( )倍是0.0328
3280
3.28
1000
1000
扩大10倍
缩小100倍
填一填
1.把2.32的小数点向右移动两位,它就扩大到原数的( )倍。
3.把3.75扩大100倍,小数点 向( )移动( )位,是( ).
6.把0.073的小数点向( )移动( )位,原数就变成730。
5.把140的小数点向( )移动( )位,原数变成0.14。
2.把2.32的小数点向左移动两位,它就缩小到原数的( )。
4.把3.75缩小到它的 ,小数点 向( )移动( )位,是( )
100
1
100
100
1
右
两
左
两
三
左
四
右
375
0.0375
7、生活中常用的单位:
质量:1吨=1000千克 1千克=1000克
长度:1千米=1000米 1分米=10厘米 1厘米=10毫米
1分米=100毫米 1米=10分米=100厘米
面积:1平方米= 100平方分米
1平方分米=100平方厘米
1平方千米=100公顷 1公顷=10000平方米
人民币: 1元=10角 1角=10分 1元=100分
高级单位
低级单位
×进率
÷进率
50厘米=( )米 1.2米=( )分米
0.8平方千米=( )公顷
600平方米=( )公顷
15分=( )元 8.09吨=( )千克
0.5
12
80
0.06
0.15
8090
52米4厘米=( )米
1吨25千克=( )吨
2.37米=( )厘米
52.04
237
1.025
填一填。
1米6厘米=( )米 9千克9克( )千克
5米7分米=( )分米
1.98千米=( )千米( )米
2.06吨=( )吨( )千克
7元3分=( )元
1.06
9009
57
1
980
2
60
7.03
8、小数的近似数(用“四舍五入”的方法):
(1)保留整数,表示精确到个位,要看十分位,把它四舍五入。
(2)保留一位小数,表示精确到十分位,要看小数的第二位,把它四舍五入。
(3)保留两位小数,表示精确到百分位,要看小数的第三位,把它四舍五入。
注意:在表示近似数时,小数末尾的0不能去掉。
求下面小数的近似数。
(1) 0.2563 12.0049 (精确到百分位)
(2) 7.816 13.974 (省略十分位后面的尾数)
(3) 1.234 25.519 (精确到个位)
≈0.26
≈12.00
≈7.8
≈14.0
≈1
≈26
(4)一个三位小数约等于0.36,它可能是多少?
其中最大是( ),最小是( )。
0.364
0.355
(5)改写成用“万”做单位的数,并保留一位小数
204500 = ( )≈( )
7100=( )≈( )
39800=( )≈( )
(6)改写成用“亿”作单位的数,并精确到百分位。
743200000=( )≈( )
53900000=( )≈( )
499500000=( )≈( )
20.45万
20.5万
0.71万
0.7万
3.98万
4.0万
7.432亿
7.43亿
0.539亿
0.54亿
4.995亿
5.00亿
知识点五:小数的加法和减法
1、小数的加、减法要注意:小数点要对齐也就是把数位对齐,得数的末尾有0,一般要把0去掉。
2、整数的运算定律(以及简便的方法)在小数运算中同样适用。
练习五
5.6+2.7+4.4
9.14-1.43-4.57
9.5+4.85-6.13
77+2.7+2.3+25
10.75+0.4-9.86
51.27-8.66-1.34
1、怎样简便就怎样算。
知识点六:三角形
1、由三条线段围成的图形(每相邻两条线段的端点
相连)叫做三角形。
2、从三角形的一个顶点到它的对边做一条垂线,顶
点到垂足之间的线段叫做三角形的高,这条边叫
做三角形的底。三角形只有3条高。
3、三角形具有稳定性。
4、三角形任意两边之和大于第三边。
5、三个角都是锐角的三角形叫做锐角三角形。
6、有一个角是直角的三角形叫做直角三角形。
7、有一个角是钝角的三角形叫做钝角三角形。
8、每个三角形都最少有两个锐角;每个三角形都最
多有1个直角;每个三角形都最多有1个钝角。
9、两条边相等的三角形叫做等腰三角形。
10、三条边都相等的三角形叫等边三角形,也叫正三
角形。
11、等边三角形是特殊的等腰三角形
12、三角形的内角和是180°。
13、四边形的内角和是360°
14、用2个相同的三角形可以拼成一个平行四边形。
15、用2个相同的直角三角形可以拼成一个平行四边
形、一个长方形、一个大三角形。
16、用2个相同的等腰的直角的三角形可以拼成一个
平行四边形、一个正方形。一个大的等腰的直角
的三角形。
一、填空。
1、锐角三角形中有( )个锐角;直角三角形中有( )个直角, ( )个锐角;钝角三角形中有( )个钝角, ( )个锐角。
2、直角三角形的三个角中,最大的一个角是( )度,另外两个角都是( )角。
3、做房屋的金字架是运用了三角形( )的特性。
4、一个等腰三角形的一个底角是55度,它的顶角是( )度,还可以说,它是一个( )三角形。
5、三个完全一样的三角形可以拼成一个( )形,至少要( )个完全一样的三角形才能拼成一个正方形。
6、按照三角形中边的不同,三角形可以分为( )和( )这两类特殊的三角形。
练习六
3
1
2
1
2
90
锐
稳定
70
锐角
梯
2
等腰三角形
等边三角形
1、一个三角形最少有( )个锐角,最多有( )个直角。
二、选择
A、1 1 B、2 1 C、3 2
2、一个三角形中,最多有( )个钝角。
A、3 B、2 C、1
3、一个直角三角形,已知一个角是25度,则第三个角是( )度。
A、75° B、65° C、165°
4、正三角形每个角都是( )度。
A、90° B、100° C、60°
5、一个三角形,已知两个角分别是50°和70°,则第三个角是( )度。
A、60° B、90° C、80°
B
C
B
C
A
三、解决问题
1、张明做一个等边三角形的风筝,风筝的周长是270厘米。这个风筝每条边的长是多少厘米?
2、一条红领巾的一个底角是30度,它的顶角是多少度?
3、边长为12厘米的正方形铁丝框,拆开后围成一个最大的等边三角形。这个等边三角形的边长是多少厘米?
4、一块等腰三角形绿地,它的周长是185米,一条腰长是52米,它的底边长多少米?
270÷3=90(厘米)
答:这个风筝每条边的长是90厘米。
30×2=60°
180°-60°=120°
答:它的顶角是120°。
答:这个等边三角形的边长是16厘米。
12×4=48(厘米)
48÷3=16(厘米)
52×2=104(米)
185-104=81(米)
答:它的底边长81米。
5、一个三角形的两条边分别是7cm和4cm,第三条边的长可能是多少?(答案取整数)
7-4=3(cm)
7+4=11(cm)
第三条边大于3厘米且小于11厘米。
答:第三条边的长可能是4厘米、5厘米、6厘米、7厘米、8厘米、9厘米、 10厘米。
条形统计图优点:直观地反映数量的多少。
折线统计图优点:既可以反映数量的多少,又能反映数量的增减变化。
折线统计图中,变化趋势指:上升或者下降。
知识点七 :统 计
(1)( )年沙尘暴总天数最多,( )年沙尘暴总天数最少。
(2)13年以来沙尘暴总天数的整体趋势为( )。
(3)从图上你还能得到哪些信息?你有什么好的建议?
1991年
1998年
沙尘暴天数有所下降,但每年仍持续半个月之久 。
2090
2162
2210
2253
2366
2476
2622
答:呈上升趋势。
要表示凉鞋销售的变化情况,用哪种统计图比较好呢?
根据统计图回答下列问题:
①说一说销售量的变化情况, 想一想变化的原因。
②如果每月卖出60双凉鞋便能收回成本,那么有哪几个月盈利?哪几个月亏本?哪几个月不亏不盈?
③你认为去年销售量的统计对以后鞋店确定进货数量有什么帮助?
2005年凉鞋销售量统计图
30
20
60
70
140
230
350
320
180
80
30
10
0
知识点八 :数学广角
(一)植树问题:
1、 两端要栽:间隔数=总长÷间距; 总长=间距×间隔数;
棵数=间隔数+1; 间隔数=棵数-1
2、 两端不栽:间隔数=总长÷间距; 总长=间距×间隔数;
棵数=间隔数-1; 间隔数=棵数+1
(二)锯木问题: 段数=次数+1; 次数=段数-1
总时间=每次时间×次数
(三)方阵问题:
最外层的数目是:边长×4-4或者是(边长-1)×4
整个方阵的总数目是:边长×边长
(四)封闭的图形(例如围成一个圆形、椭圆形):
总长÷间距=间隔数;棵数=间隔数
两端栽
两端不栽
锯木问题
方阵问题
封闭图形
1、园林工人要在长400米的路的一侧栽树,每隔8米栽一棵,两端都要栽。一共要栽多少棵树?
400÷8=50(棵)
50+1=51(棵)
答:一共要栽51棵。
练习八
2、在一条全长180米的街道两旁安装路灯,
(两端都要安装),每隔6米安一座。一共
要安装多少座路灯?
180÷6=30(个)
30+1=31(座)
31×2=62 (座)
答:一共要安装62座路灯。
3、园林工人沿公路一侧植树 ,每隔 6米种一棵,一共种了36棵。从第1棵到最后一棵的距离有多远?
36-1=35( 个)
6×35=210(米)
答:从第1棵到最后一棵的距离有210米远。
4、两棵大树之间相距250米,园林部门计划在两棵大树中间补栽小树,使每两棵小树之间的距离是10米,一共要补栽多少棵小树?
250÷10=25(个)
25-1=24(棵)
答:一共要补栽24棵小树。
5、永兴小学教学楼与实验楼相距120米,要在道路两侧栽树,每两棵树之间的距离是8米。这条路上一共有多少棵树?
120÷8=15(个)
15-1=14(棵)
14×2=28(棵)
答:一共有28棵树。
大营希望小学
6、 一根木头长10米,要把它平均分成5段。每锯下一段需要8分钟,锯完一共要花多少分钟?
大营希望小学
5-1=4(次)
4×8=32(分)
答:锯完一共要花32分钟。
大营希望小学
7、酒店里的大钟4时敲4下,6秒敲完,10时敲响10下,需要多长时间?
大营希望小学
4-1=3(个)
6÷3=2(秒)
10-1=9(个)
9×2=18(秒)
答:需要18秒。
8、小明从1楼到3楼需走36级台阶,小明从1楼到6楼需走多少级台阶
36÷(3-1)=18(级)
18×(6-1)=90(级)
答:小明从1楼到6楼需
走90级台阶。
8、在正方形的水池边摆花盆,使每边都有5盆花,可以怎样摆?一共需要多少盆花?
第一种摆法:每边5盆,顶角不摆。
5×4=20(盆)
答:一共需要20盆。
第二种摆法:每边5盆,顶角要摆。
(5-1)×4=16(盆)
答:一共需要16盆。
或 5×4-4=16(盆)
9、24名学生围成一个正方形做游戏,每边人数相等,四个顶点都有人,每边各有多少名学生?
24÷4=6(人)
6+1=7(人)
答:每边各有7名学生。
圆形花坛的一周全长50米,如果沿着这一圈每隔2米摆放一盆花,一共需要多少盆花?
10、
50÷2=25(盆)
答:一共需要25盆。
11、
150÷15=10(盏)
答:一共需要10盏灯。
