山东省东营市垦利区郝家镇七年级数学下册第4章三角形4.5利用三角形全等测距离同步练习(新版)北师大版
文档属性
| 名称 | 山东省东营市垦利区郝家镇七年级数学下册第4章三角形4.5利用三角形全等测距离同步练习(新版)北师大版 | 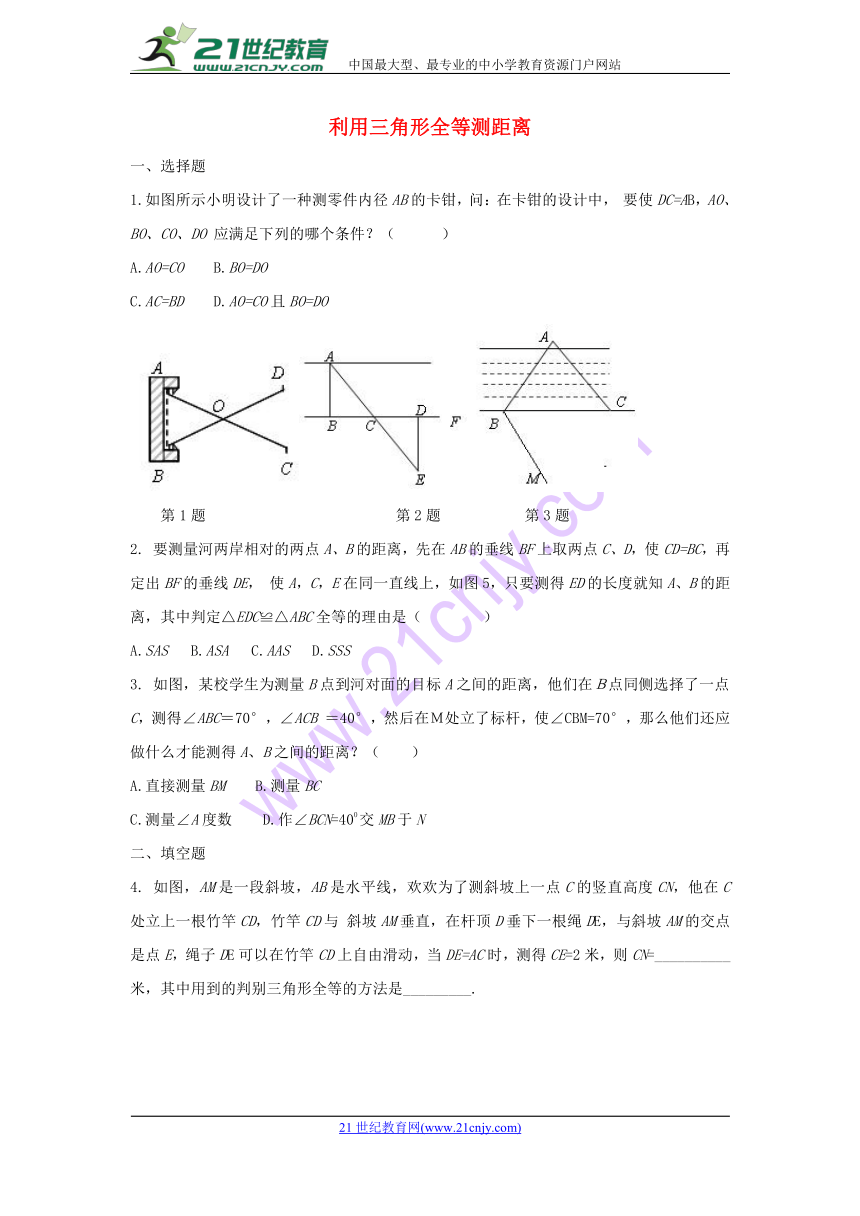 | |
| 格式 | zip | ||
| 文件大小 | 174.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-04-17 10:02:24 | ||
图片预览


文档简介
利用三角形全等测距离
一、选择题
1.如图所示小明设计了一种测零件内径AB的卡钳,问:在卡钳的设计中, 要使DC=AB,AO、BO、CO、DO 应满足下列的哪个条件?( )21教育网
A.AO=CO B.BO=DO
C.AC=BD D.AO=CO且BO=DO
第1题 第2题 第3题
2. 要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE, 使A,C,E在同一直线上,如图5,只要测得ED的长度就知A、B的距离,其中判定△EDC≌△ABC全等的理由是( )【来源:21·世纪·教育·网】
A.SAS B.ASA C.AAS D.SSS
3. 如图,某校学生为测量B点到河对面的目标A之间的距离,他们在B点同侧选择了一点C,测得∠ABC=70°,∠ACB =40°,然后在M处立了标杆,使∠CBM=70°,那么他们还应做什么才能测得A、B之间的距离?( )21·世纪*教育网
A.直接测量BM B.测量BC
C.测量∠A度数 D.作∠BCN=400交MB于N
二、填空题
4. 如图,AM是一段斜坡,AB是水平线,欢欢为了测斜坡上一点C的竖直高度CN,他在C处立上一根竹竿CD,竹竿CD与 斜坡AM垂直,在杆顶D垂下一根绳DE,与斜坡AM的交点是点E,绳子DE可以在竹竿CD上自由滑动,当DE=AC时,测得CE=2米,则CN=__________米,其中用到的判别三角形全等的方法是_________.www-2-1-cnjy-com
第4题 第5题
5. 在修建秦山隧道时,为加快施工进度,需要从隧道A、B两端同时施工,如图,先在地上取一个可以直接达到A点和B点的点C,连结AC并延长到D,使CD=AC,连结BC并延长到E,使CE=CB,连结DE,测量出∠D=550,∠E=520,为使两处施工能顺利接通,要保证他们的施工方向∠A需等于_____°,∠B=_______°.21*cnjy*com
6. 欢欢家和盈盈家所居住的两幢楼的地基在同一水平面上,且高度相同.有一天,欢欢对盈盈说:“从我住的这幢楼的底部到你住的那幢楼的顶部的直线距离,等于从你住的那幢楼的底部到我住的这幢楼的顶部的直线距离.”你认为欢欢的话正确吗?答:______.其中用到的判别三角形全等的方法是_________.【来源:21cnj*y.co*m】
7.如图,某人在楼顶A点处看到一烟囱顶端B的仰角∠BAD=42°,看到烟囱底部C的俯角∠CAD也是42°,如果楼高AE是15米,那么烟囱高__________米.【出处:21教育名师】
第7题 第8题
8. 明明是个善于观察思考的学生,通过长期观察发现,他家楼房AB一年四季中影子最长是25.1米,如图,太阳光线是平行的,那么同样高的两栋楼房至少相距_____米才能互不影响采光.【版权所有:21教育】
三、解答题
9. 如图①,河边有一条笔直的公路l,公路两侧是平坦的草地.在数学活动课上,老师要求测量河对岸B点到公路的距离,请你设计一个测量方案.要求:21教育名师原创作品
(1)列出你测量所使用的测量工具;
(2)画出测量的示意图,写出测量的步骤;
(3)用字母表示测得的数据,求出B点到公路的距离.
① ②
10. 某城市搞亮化工程,如图,在甲楼底部、乙楼顶部分别安装一盏射灯。已知A灯恰好照到B灯,B灯恰好照到甲楼的顶部,如果两盏灯的光线与水平线的夹角相等,那么能否说甲楼的高度是乙楼的2倍?说说你的看法.21cnjy.com
11. 某铁路施工队在建设铁路的过程中,需要打通一座小山,设计时要测量隧道的长度.小山前面恰好是一块空地,利用这样的有利地形,测量人员是否可以利用三角形全等的知识测量出需要开挖的隧道的长度?说明道理.?21·cn·jy·com
参考答案
1.D 2.B 3.D 4.AAS 5. 550,73° 6. 正确,SAS 7. 30 8.25.1 9. ①在公路上取一点A,用测角器测得∠A=90o;②在公路上取一点C,用尺子测出AC的长,记为m米;③用测角器测得∠ACB=;④在公路的下方过点C作射线CM,使∠ACM=∠ACB =,交BA的延长线于点D;21世纪教育网版权所有
⑤用尺子测出AD的长,记为n米.(3)由测量步骤知,
在△BAC和△DAC中, 所以△BAC≌△DAC(ASA).所以AD=AC.因此B点到公路的距离为n米.www.21-cn-jy.com
10. 如图,过点B作AC的垂线交AC于D.∵∠CBD=∠ABD,BD⊥AC,BD=BD,∴△ABD≌△CBD,∴CD=DA.∴AC=2DA.2·1·c·n·j·y
11. 解:方法:可在空地上取一个能直接到达A点、B点的点O,连结AO延长到D,使OD=OA;连接BO延长到E,使OE=OB。连结DE并测出它的长度,则DE的长就是A、B间的距离.如图所示:?2-1-c-n-j-y
△AOB和△DOE中,∴△AOB≌△DOE(SAS)∴AB=DE(全等三角形,对应边相等).?
一、选择题
1.如图所示小明设计了一种测零件内径AB的卡钳,问:在卡钳的设计中, 要使DC=AB,AO、BO、CO、DO 应满足下列的哪个条件?( )21教育网
A.AO=CO B.BO=DO
C.AC=BD D.AO=CO且BO=DO
第1题 第2题 第3题
2. 要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE, 使A,C,E在同一直线上,如图5,只要测得ED的长度就知A、B的距离,其中判定△EDC≌△ABC全等的理由是( )【来源:21·世纪·教育·网】
A.SAS B.ASA C.AAS D.SSS
3. 如图,某校学生为测量B点到河对面的目标A之间的距离,他们在B点同侧选择了一点C,测得∠ABC=70°,∠ACB =40°,然后在M处立了标杆,使∠CBM=70°,那么他们还应做什么才能测得A、B之间的距离?( )21·世纪*教育网
A.直接测量BM B.测量BC
C.测量∠A度数 D.作∠BCN=400交MB于N
二、填空题
4. 如图,AM是一段斜坡,AB是水平线,欢欢为了测斜坡上一点C的竖直高度CN,他在C处立上一根竹竿CD,竹竿CD与 斜坡AM垂直,在杆顶D垂下一根绳DE,与斜坡AM的交点是点E,绳子DE可以在竹竿CD上自由滑动,当DE=AC时,测得CE=2米,则CN=__________米,其中用到的判别三角形全等的方法是_________.www-2-1-cnjy-com
第4题 第5题
5. 在修建秦山隧道时,为加快施工进度,需要从隧道A、B两端同时施工,如图,先在地上取一个可以直接达到A点和B点的点C,连结AC并延长到D,使CD=AC,连结BC并延长到E,使CE=CB,连结DE,测量出∠D=550,∠E=520,为使两处施工能顺利接通,要保证他们的施工方向∠A需等于_____°,∠B=_______°.21*cnjy*com
6. 欢欢家和盈盈家所居住的两幢楼的地基在同一水平面上,且高度相同.有一天,欢欢对盈盈说:“从我住的这幢楼的底部到你住的那幢楼的顶部的直线距离,等于从你住的那幢楼的底部到我住的这幢楼的顶部的直线距离.”你认为欢欢的话正确吗?答:______.其中用到的判别三角形全等的方法是_________.【来源:21cnj*y.co*m】
7.如图,某人在楼顶A点处看到一烟囱顶端B的仰角∠BAD=42°,看到烟囱底部C的俯角∠CAD也是42°,如果楼高AE是15米,那么烟囱高__________米.【出处:21教育名师】
第7题 第8题
8. 明明是个善于观察思考的学生,通过长期观察发现,他家楼房AB一年四季中影子最长是25.1米,如图,太阳光线是平行的,那么同样高的两栋楼房至少相距_____米才能互不影响采光.【版权所有:21教育】
三、解答题
9. 如图①,河边有一条笔直的公路l,公路两侧是平坦的草地.在数学活动课上,老师要求测量河对岸B点到公路的距离,请你设计一个测量方案.要求:21教育名师原创作品
(1)列出你测量所使用的测量工具;
(2)画出测量的示意图,写出测量的步骤;
(3)用字母表示测得的数据,求出B点到公路的距离.
① ②
10. 某城市搞亮化工程,如图,在甲楼底部、乙楼顶部分别安装一盏射灯。已知A灯恰好照到B灯,B灯恰好照到甲楼的顶部,如果两盏灯的光线与水平线的夹角相等,那么能否说甲楼的高度是乙楼的2倍?说说你的看法.21cnjy.com
11. 某铁路施工队在建设铁路的过程中,需要打通一座小山,设计时要测量隧道的长度.小山前面恰好是一块空地,利用这样的有利地形,测量人员是否可以利用三角形全等的知识测量出需要开挖的隧道的长度?说明道理.?21·cn·jy·com
参考答案
1.D 2.B 3.D 4.AAS 5. 550,73° 6. 正确,SAS 7. 30 8.25.1 9. ①在公路上取一点A,用测角器测得∠A=90o;②在公路上取一点C,用尺子测出AC的长,记为m米;③用测角器测得∠ACB=;④在公路的下方过点C作射线CM,使∠ACM=∠ACB =,交BA的延长线于点D;21世纪教育网版权所有
⑤用尺子测出AD的长,记为n米.(3)由测量步骤知,
在△BAC和△DAC中, 所以△BAC≌△DAC(ASA).所以AD=AC.因此B点到公路的距离为n米.www.21-cn-jy.com
10. 如图,过点B作AC的垂线交AC于D.∵∠CBD=∠ABD,BD⊥AC,BD=BD,∴△ABD≌△CBD,∴CD=DA.∴AC=2DA.2·1·c·n·j·y
11. 解:方法:可在空地上取一个能直接到达A点、B点的点O,连结AO延长到D,使OD=OA;连接BO延长到E,使OE=OB。连结DE并测出它的长度,则DE的长就是A、B间的距离.如图所示:?2-1-c-n-j-y
△AOB和△DOE中,∴△AOB≌△DOE(SAS)∴AB=DE(全等三角形,对应边相等).?
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
