一次方程组复习提高卷（含答案）

七年级数学下一次方程组复习提高卷
姓名： 日期：
一、单选题
1.对于非零的两个实数a，b，规定a⊕b=am﹣bn，若3⊕（﹣5）=15，4⊕（﹣7）=28，则（﹣1）⊕2的值为（?? ） 21世纪教育网版权所有
A.?﹣13????????????????????????????????????????B.?13????????????????????????????????????????C.?2????????????????????????????????????????D.?﹣2
2.某车间有56名工人，每人每天能生产螺栓16个或螺母24个，设有x名工人生产螺栓，y名工人生产螺母，每天生产的螺栓和螺母按1：2配套，下面所列方程组正确的是（　　）
A.???????????????B.???????????????C.???????????????D.?
3.若关于，的方程组的解是，则为（??? ）
A.?1???????????????????????????????????????????B.?3???????????????????????????????????????????C.?5???????????????????????????????????????????D.?2
4.为迎接2013年“亚青会”，学校组织了一次游戏：每位选手朝特制的靶子上各投三以飞镖，在同一圆环内得分相同．如图所示，小明、小君、小红的成绩分别是29分、43分和33分，则小华的成绩是（???）?????????????????????21cnjy.com
A.?31分????????????????????????????????????B.?33分????????????????????????????????????C.?36分????????????????????????????????????D.?38分
5.如图，AB⊥BC，∠ABD的度数比∠DBC的度数的两倍少15°，设∠ABD和∠DBC的度数分别为x°、y°，那么下面可以求出这两个角的度数的方程组是（　　） A.???????????B.??????????C.?????????D.?www.21-cn-jy.com
二、填空题（共5题；共18分）
6.如图所示的两架天平保持平衡，且每块巧克力的质量相等，每个果冻的质量也相等，则一块巧克力的质量为________g．?????????
第6题图 第8题图
7.若方程 的解中，x、y互为相反数，则 ________ ________?
8.如上图，两根铁棒直立于桶底水平的木桶中，在桶中加入水后，一根铁棒的露出水面，另一根铁棒的露出水面．两根铁棒长度之和为34cm，此时木桶中水的深度是　________?cm．2·1·c·n·j·y
9.已知非负数a,b,c满足条件3a+2b+c=4.? 2a+b+3c=5.? 设s=5a+4b+7c的最大值为m，最小值为n． 则n-m的值为________. 【来源：21·世纪·教育·网】
10.如下图所示，高速公路上，一辆长为4米，速度为110千米/时的轿车准备超越一辆长为12米，速度为100千米/时的卡车，则轿车从开始追赶到超越卡车，需要花费的时间约是________秒（结果保留整数）.21·世纪*教育网
三、计算题
11.解下列方程组（1） （2） （3）
四、解答题
12.若关于 、 的二元一次方程组 的解中x与y的值互为相反数，求 的值；

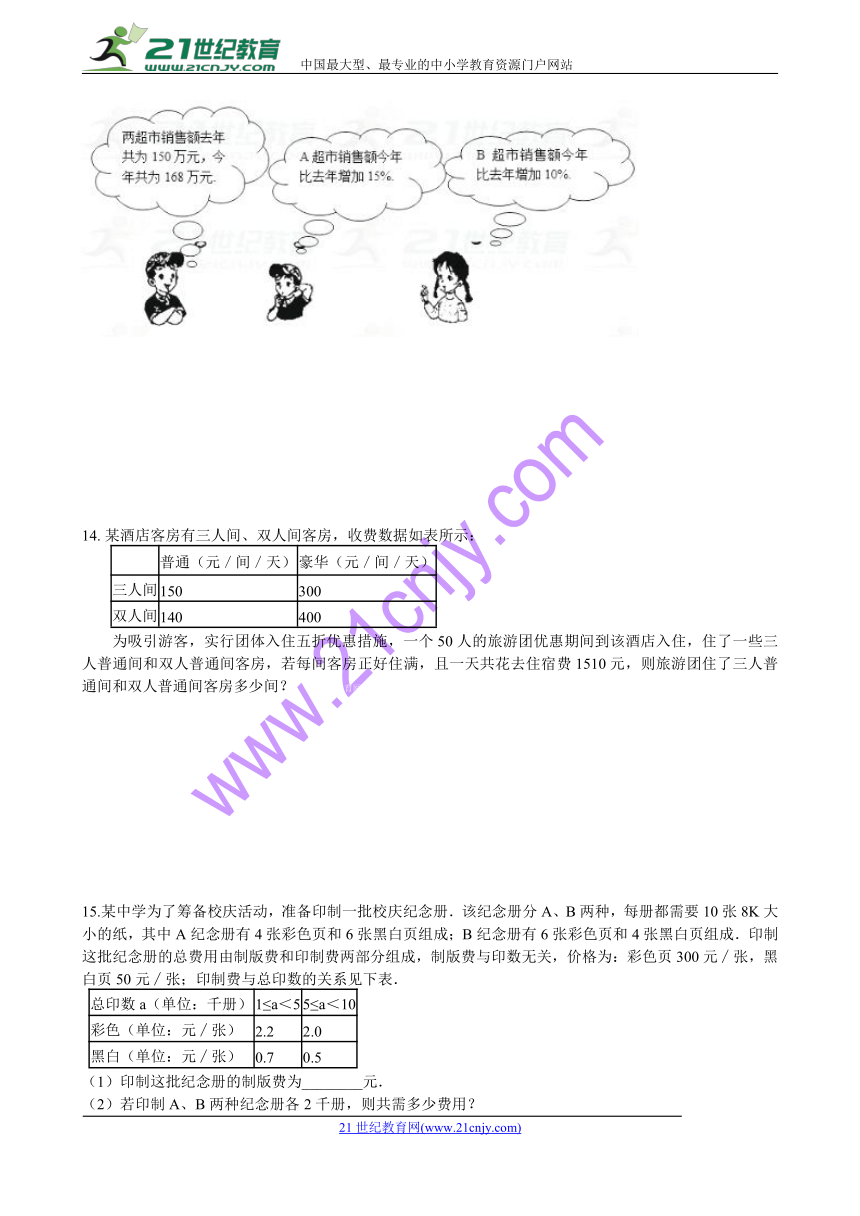
13.七年级某班的一个综合实践活动小组去A、B两个超市调查去年和今年“春节”期间的销售情况，下图是调查后小敏与其它两位同学进行交流的情景．根据他们的对话，请你分别求出A、B两个超市今年“春节”期间的销售额．
14.?某酒店客房有三人间、双人间客房，收费数据如表所示：
普通（元／间／天）
豪华（元／间／天）
三人间
150
300
双人间
140
400
为吸引游客，实行团体入住五折优惠措施，一个50人的旅游团优惠期间到该酒店入住，住了一些三人普通间和双人普通间客房，若每间客房正好住满，且一天共花去住宿费1510元，则旅游团住了三人普通间和双人普通间客房多少间？ 21教育网
15.某中学为了筹备校庆活动，准备印制一批校庆纪念册．该纪念册分A、B两种，每册都需要10张8K大小的纸，其中A纪念册有4张彩色页和6张黑白页组成；B纪念册有6张彩色页和4张黑白页组成．印制这批纪念册的总费用由制版费和印制费两部分组成，制版费与印数无关，价格为：彩色页300元∕张，黑白页50元∕张；印制费与总印数的关系见下表． www-2-1-cnjy-com
总印数a（单位：千册）
1≤a＜5
5≤a＜10
彩色（单位：元∕张）
2.2
2.0
黑白（单位：元∕张）
0.7
0.5
（1）印制这批纪念册的制版费为________元．
（2）若印制A、B两种纪念册各2千册，则共需多少费用？
（3）如果该校共印制了A、B两种纪念册6千册，一共花费了75500元，则该校印制了A、B两种纪念册各多少册？ 21·cn·jy·com
五、附加题
16.已知一个四位数的十位数字加1等于它的个位数字，个位数字加1等于它的百位数字，把这个四位数倒序排列所成的数与原数的和等于10769，则该四位数的数字之和为（　　）2-1-c-n-j-y

答案解析部分
一、单选题
1.【答案】A
【考点】解二元一次方程组
【解析】【解答】解：根据题意得：3⊕（﹣5）=3m+5n=15，4⊕（﹣7）=4m+7n=28 ∴ ，解得： ∴（﹣1）⊕2=﹣m﹣2n=35﹣48=﹣13故选A．【分析】根据已知规定及两式，确定出m、n的值，再利用新规定化简原式即可得到结果．
2.【答案】A
【考点】二元一次方程组的应用
【解析】【分析】此题中的等量关系有：①生产螺栓人数+生产螺母人数=56人；②每天生产的螺栓和螺母按1：2配套，那么螺栓要想与螺母的数量配套，则螺栓数量的2倍=螺母数量。【解答】根据生产螺栓人数+生产螺母人数=56人，得方程x+y=56；根据螺栓数量的2倍=螺母数量，得方程2×16x=24y．列方程组为故选A．【点评】本题考查了由实际问题抽象出二元一次方程组，难点在于理解第二个等量关系：若要保证配套，则生产的螺母的数量是生产的螺栓数量的2倍，所以列方程的时候，应是螺栓数量的2倍=螺母数量。
3.【答案】D
【考点】二元一次方程组的解
【解析】【分析】由题意把代入方程组即可得到关于m、n的方程组，解出m、n的值，最后根据绝对值的规律求解即可.【解答】由题意得，解得，则故选D.【点评】解题的关键是熟练掌握方程组的解的定义：同时适合方程组的两个方程的解叫作方程组的解.
4.【答案】C
【考点】解三元一次方程组
【解析】【分析】设特制的靶子从里向外的分值依次为a，b，c；如图所示，小明、小君、小红的成绩分别是29分、43分和33分，则；小华的成绩=a+b+c=36分选C【点评】本题考查解方程组，掌握方程组的解法是本题的关键。
5.【答案】B
【考点】二元一次方程组的应用
【解析】【解答】设∠ABD和∠DBC的度数分别为x°、y°，
由题意得，． 故选B．
【分析】根据两角互余和题目所给的关系，列出方程组．本题考查了由实际问题抽象出二元一次方程组，解答本题的关键是根据题意找出合适的等量关系列方程组．
二、填空题
6.【答案】20
【考点】二元一次方程组的应用
【解析】【解答】设每块巧克力的质量是 g，每个果冻的质量是 g，则 ，解得 ．【分析】设每块巧克力的质量是 g，每个果冻的质量是 g，根据题目给出的等量关系建立方程组，然后解出x、y的值，再代入计算即可．
7.【答案】；-
【考点】解二元一次方程组
【解析】【解答】因为x,y互为相反数，所以x+y=0，则，将y=-x，代入2x-y=得2x+x=，解得x=,则y=.故答案为；.【分析】根据解二元一次方程组的方法，可知构造二元一次方程组得,然后再根据二元一次方程组的解法解出x,y的值.
8.【答案】12
【考点】二元一次方程组的应用
【解析】解：设较长铁棒的长度为xcm，较短铁棒的长度为ycm，由题意得：， 解得：， 因此木桶中水的深度为18×=12（cm），故答案为：12．【分析】设较长铁棒的长度为xcm，较短铁棒的长度为ycm．因为两根铁棒之和为34cm，故可的方程：x+y=34，又知两棒未露出水面的长度相等，又可得方程x=y，把两个方程联立，组成方程组，解方程组可得较长的铁棒的长度，用较长的铁棒的长度×可以求出木桶中水的深度．
9.【答案】-2
【考点】解三元一次方程组
【解析】【解答】已知，3a+2b+c=4①，2a+b+3c=5②，②×2?①得，a+5c=6，a=6?5c ， ①×2?②×3得，b?7c=?7，b=7c?7，又已知a、b、c为非负实数，所以，6?5c?0，7c?7?0，可得, ?，S=5a+4b+7c=5×(6?5c)+4×(7c?7)+7c=10c+2，所以10?10c?12，12?10c+2=S?14，即m=14，n=12，n?m=?2，故答案为?2.
10.【答案】6
【考点】二元一次方程组的应用
【解析】【解答】设整个超越过程历时x小时，在这一过程中卡车行驶了y千米，则轿车行驶了（y＋0.012＋0.004）千米，则 ，解得x＝0.0016（小时），0.0016小时＝5.76秒≈6秒．【分析】列二元一次方程组解应用题的关键是通过审题确定题目中的相等关系，再利用相等关系列出方程组．
三、计算题
11.【答案】解：（1）①+②得：3x=15，即x=5，把x=5带点人①得：y=2，则方程组的解为；（2）方程组整理得：， ①×4﹣②得：5y=25，即y=5，把y=5代入①得：x=﹣2，则方程组的解为；（3）， ③﹣①得：x﹣2y=﹣8④，②﹣④得：y=9，把y=9代入④得：x=10，把x=10，y=9代入①得：z=7，则方程组的解为．
【考点】解二元一次方程组
【解析】【分析】（1）方程组利用加减消元法求出解即可；（2）方程组整理后，利用加减消元法求出解即可；（3）方程组利用加减消元法求出解即可．
四、解答题
12.【答案】因为x与y互为相反数，则y=-x，将其代代方程组，化简得 将（1）代入（2）得5x=18-4x解得x=2.将x=2代入（1）得a=8.
【考点】解二元一次方程组
【解析】【分析】二元一次方程组中含有参数 a，可将y=-x代入方程组，即可将方程组化成二元一次方程组，从而按其解法解出x和a的值.
13.【答案】解：设去年A超市销售额为x, B超市销售额为y，由题意得：?????????? ，解得 ?? ?所以 ， .??? 答：今年A超市销售额为69万元, B超市销售额为99万元.
【考点】二元一次方程组的应用
【解析】【分析】根据对话找出两个等量关系：（1）去年的A超市销售额+去年的B超市销售额=150；（2）今年的A超市销售额+今年的B超市销售额=168.增减百分率问题：其中a>b，a比b多,b比a少.
14.【答案】解：设三人普通房和双人普通房各住了x、y间．根据题意，得： 化简，得： 解之，得：答：三人间普通客房、双人间普通客房各住了8、13间
【考点】二元一次方程组的应用
【解析】【分析】本题最后的问题是旅游团住了三人普通间和双人普通间客房各多少间，跟表中的豪华间是没有关系的．那么根据人数和钱数就可以得到两个等量关系：三人普通间的人数+双人普通间的人数=50；三人普通间的钱数+双人普通间的钱数=1510．
15.【答案】（1）3500（2）解：∵印制A、B两种纪念册各2千册， ∴共需：2000（4×2.2+6×0.7+6×2.2+4×0.7）+3500=61500（元），答：印制A、B两种纪念册各2千册，则共需61500元（3）解：设A纪念册x册，B纪念册y册，根据题意得出： ，解得： ．答：该校印制了A、B两种纪念册各4000册，2000册
【考点】二元一次方程组的应用
【解析】【解答】解：（1）∵A纪念册有4张彩色页和6张黑白页组成；B纪念册有6张彩色页和4张黑白页组成，彩色页300元∕张，黑白页50元∕张， ∴印制这批纪念册的制版费为：4×300+6×50+6×300+4×50=3500（元）；【分析】（1）根据A纪念册有4张彩色页和6张黑白页组成；B纪念册有6张彩色页和4张黑白页组成，彩色页300元∕张，黑白页50元∕张，求其和即可；（2）根据题意可得等量关系：各印一册A，B种纪念册的印刷费用×2000+制版费=总费用，再算出结果即可；（3）根据（2）中计算方法，得出关于A、B两种纪念册6千册，一共花费了75500元的方程组求出即可．
五、附加题
16.【答案】A
【考点】解三元一次方程组
【解析】【解答】解：设这个四位数为abcd，则abcd+dcba=10769；则b+c=16；又据题意可知，c=d﹣1，b=d+1，则b+c=（d﹣1）+（d+1）=16，可得：d=8，又∵a+d=8+1+a=10，∴a=1，综上可知，a=1，d=8，c=8﹣1=7，b=8+1=9，所以该四位数的数字之和为25．故选A．【分析】设这个四位数为abcd，则， 可以发现（b+c）和的个位为6，b+c=16；据题意可知，c=d﹣1，b=d+1，则b+c=（d﹣1）+（d+1）=16，则d=8，又a+d=8+1+a=10，则a=1；综上可知，a=1，d=8，c=8﹣1=7，b=8+1=9．